Computationally Efficient Direction of Arrival Estimation for Improved Nested Linear Array

LIN Xinping，ZHOU Mengjie，ZHANG Xiaofei*，LIJianfeng

1.College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；2.Laboratory of Dynamic Cognitive System of Electromagnetic Spectrum Space，Ministry of Industry and Information Technology，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China

Abstract:Nested linear array enables to enhance localization resolution and achieve under-determined direction of arrival（DOA）estimation.In this paper，the traditional two-level nested linear array is improved to achieve more degrees of freedom（DOFs）and better angle estimation performance.Furthermore，a computationally efficient DOA estimation algorithm is proposed.The discrete Fourier transform（DFT）method is utilized to obtain coarse DOA estimates，and subsequently，fine DOA estimates are achieved by spatial smoothing multiple signals classification（SS-MUSIC）algorithm.Compared to SS-MUSIC algorithm，the proposed algorithm has the same estimation accuracy with lower computational complexity because the coarse DOA estimates enable to shrink the range of angle spectral search.In addition，the estimation of the number of signals is not required in advance by DFT method.Extensive simulation results testify the effectiveness of the proposed algorithm.

Key words:DOA estimation;nested linear array;DOFs;SS-MUSIC algorithm;computational complexity

0 Introduction

As a pivotal issue in the array signal processing，direction of arrival（DOA）estimation has attracted significant attention due to its application in many fields，such as radar，sonar，navigation and wireless communication[1-3].In the past decades，classical DOA estimation algorithms，such as multiple signals classification（MUSIC）[4]and estimation of signal parameters via rotational invariance technique（ESPRIT）[5]，have been proposed for uniform linear arrays（ULAs）[6]and uniform planar arrays（UPAs）[7].Nevertheless，the adjacent sensors of traditional uniform arrays are required to be spaced less than or equal to half wavelength to avoid spatial aliasing.

Over the years，sparse arrays，such as minimum redundancy arrays（MRAs）[8]，coprime arrays[9]and nested arrays[10]，have drawn significant attention due to the improvement of estimation accuracy，the enhancement of degrees of freedom（DOFs）and the mitigation of mutual coupling.These arrays can extend the array aperture and resolve significantly more sources than the number of physical sensors.

Among these arrays，although the MRAs can achieve the largest possible DOFs，there is no closed form expression for the sensors position and achievable DOFs.Furthermore，the design of MRAs calls for exhaustive search routines.Meanwhile，the coprime arrays are incapable of providing higher DOFs than nested arrays，which enjoy the closed form expression of sensors location，and can provide O{N2}DOFs with only N physical sensors.

In this paper，an improved nested linear array is proposed，which can provide more DOFs and achieve better angle estimation performance than the two-level nested array[10].Specifically，the improved nested array consists of three parts，a dense ULA with a hole，a sparse ULA and an additional sensor.Consequently，the difference co-array of this improved array contains a filled ULA，which can be applied to spatial smoothing based DOA estimation algorithm，such as spatial smoothing MUSIC（SSMUSIC）algorithm[10].However，SS-MUSIC algorithm suffers from tremendous computational complexity due to the global spectral search.To settle this problem，in this paper，a computational efficient DOA estimation algorithm is proposed.A traditional non-parametric spectrum analysis method called discrete Fourier transform（DFT）[11]is utilized to obtain the coarse DOA estimates without estimating the number of signals，and subsequently，the fine DOA estimates are achieved by SS-MUSIC algorithm.The proposed algorithm enables to relieve the computational burden because the coarse estimates can be exploited to shrink the range of angle spectral search.

To be more explicit，the main contributions of this paper are concluded as follows.

（1）The two-level nested linear array is improved to achieve the enhancement of DOFs and improvement of estimation accuracy.

（2）A computationally efficient DOA estimation algorithm is proposed.Compared to SS-MUSIC algorithm，the proposed algorithm has the same estimation accuracy with lower complexity because only partly angle spectral search is required.

1 Data Model

As shown in Fig.1，the improved nested linear array consists of two linear uniform subarrays and an additional sensor.The inter-element spacing of the first linear subarray with a hole containing N1sensors is d=λ/2，while the second subarray with N2sensors is d2=(N1+2)d，whereλis the wavelength.The spacing between the two subarrays is d and single additional sensor is placed collinearly with the spacing N1d to the second subarray.Thereby，the total number of sensors of the nested array is N=N1+N2+1.

Fig.1 Improved nested linear array

Setting the additional sensor as the original point，the sensors position of this nested array can be expressed as

Consequently，the array aperture of the proposed array is

Assuming that there are K far-field independent narrow band signals impinging on the improved nested linear array from anglesθ=[θ1，θ2，…，θK]，the outputs of this array can be presented as[12]

where A=[a(θ1)，a(θ2)，…，a(θK)]is the direction matrix and a(θk)is the steering vector；s(t)=[s1(t)，s2(t)，…，sK(t)]Tis the signal vector；n(t)is the additive white Gaussian noise vector withσ2nand mean zero，t=1，2，…，T and T is the total number of snapshots.

where ln(n=1，2，…，N)denotes the n th element of Ls.

The covariance matrix of outputs vector x(t)can be presented as

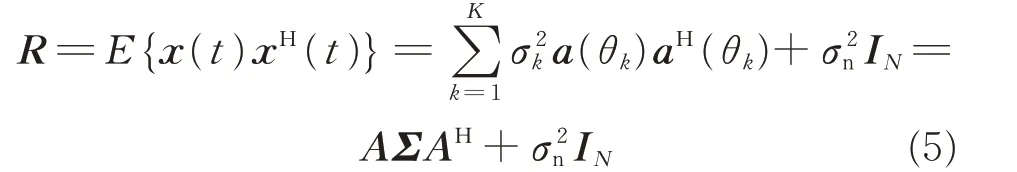
whereΣ=diag{σ21，σ22，…，σ2K}andσ2kis the average power of the k th stationary signal，IN∈RN×Nis an identity matrix.In practice，the autocorrelation matrix of the signals with finite number of snapshots is

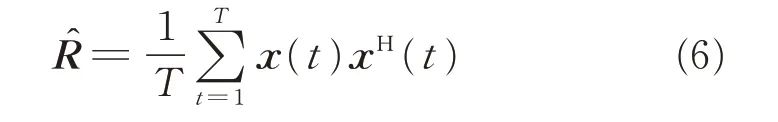
According to Ref.[13]，the autocorrelation matrix of the received signal with finite number of snapshots can be vectorized as

where⊙ denotes the Khatri-Rao product；p=is the power of additive white noise；U=vec{IN}and Ae=A*⊙A.

According to Ref.[10]，it is noted that Aein Eq.（7）can be regarded as a direction matrix of virtual array，which is named as difference co-array of the improved nested array as shown in Fig.2.A transformation for simplicity is defined as M=N1N2+2N2+N1-3 in Fig.2.

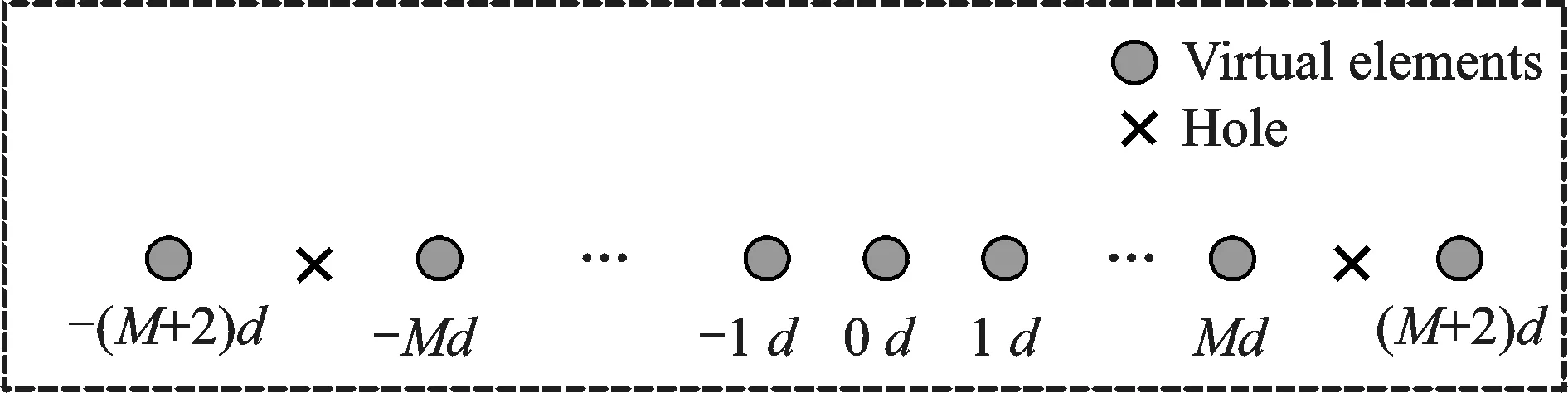
Fig.2 Difference co-array

Fig.2 depicts that the virtual array contains consecutive elements from-Md to Md，which is available for spatial smoothing based DOA estimation method[10].And hence，the available DOFs of the difference co-array can be expressed as

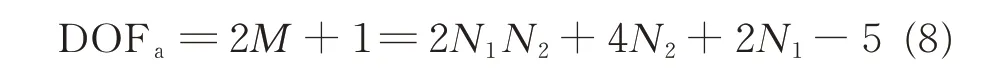
Using Eq.（8），the available DOFs can be maximized under the constraint of total number of sensors.The optimal nested arrays in Fig.1 can be obtained by the arithmetic mean-geometric mean inequalities，which are summarized in Table 1.

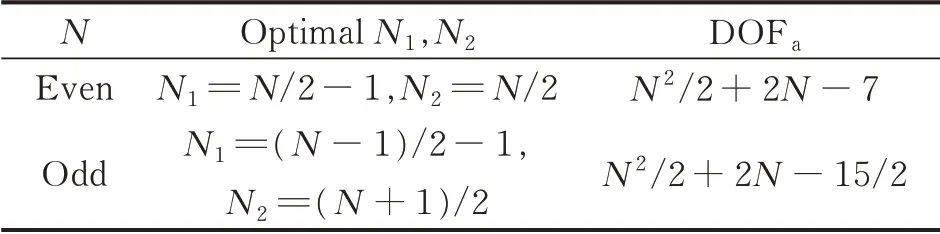
Table 1 Optimal solution for improved nested array

Remark 1Here，the proposed array is designed by decomposing the dense subarray in the two-level nested array to achieve the enhanced DOFs and mitigated mutual coupling.On the contrary，the improved nested array in Ref.[14]still incorporates the dense subarray with inter-element spacing of half wavelength，which is crucial in inducing mutual coupling effect.According to Ref.[15]，the intensity of mutual coupling is measured by coupling leakage L(M)and the coupling leakage results are provided in Table 2，where the total number of sensors is N=10.It can be seen from Table 2that the lowest mutual coupling can be achieved by the proposed array.

Table 2 Mutual coupling comparison between different arrays

2 DOA Estimation Algorithm

Here，the proposed DOA estimation algorithm for the improved nested linear array is presented.

According to Ref.[10]，after removing the repeated rows and selecting the consecutive rows of Aein Eq.（7），a new direction matrix Avcan be obtained from Aeafter sorting them，which can be denoted as

And then she confessed all her sin, and the executioner struck off her feet with the red shoes; but the shoes danced away with the little feet across the field into the deep forest.

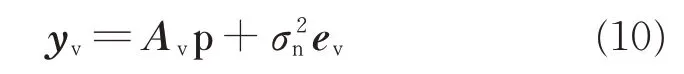
where ev∈R(2M+1)×1is a vector that one is at the(M+1)th position and the other elements are all zeros.

In Ref.[10]，SS-MUSIC algorithm is exploited to obtain DOA estimates.However，SS-MUSIC algorithm suffers from tremendous complexity.In the following part，the DFT method will be utilized to obtain the coarse DOA estimates，which can shrink the range of angle spectral search.

2.1 Coar se DOA estimation by DFT method

DFT method is a non-parametric spectrum analysis method and the resolution of DFT method depends on the number of sensors.

A normalized DFT matrix F∈C(2M+1)×(2M+1)can be defined，whose(p，q)th element is presented as

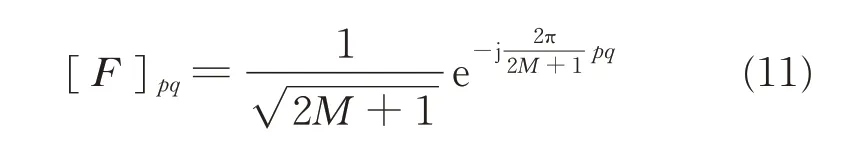
The normalized DFT of the virtual steering vector is(θk)=Fav(θk)and the p th element of(θk)is[11]

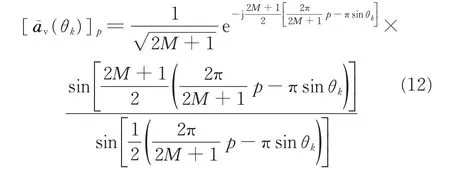
According to Ref.[11]，if the number of sensors in the virtual consecutive array is infinite，that is 2M+1→∞，there always exists an integer pk=(2M+1)sinθk/2 that makes=and the other elements are all zeros.

Hence，pk(k=1，2，…，K)can be obtained by searching the non-zero rows of a~v(θk).However，in practice，the number of sensors in an array is finite even in massive MIMO system[17].Consequently，the power of theDFT point will leak to the adjacent point，which depresses the resolution but still can be employed as an coarse estimate.

Accordingly，the DFT of the extended received signal can be obtained by z=Fyvand the p th element is presented as[18]

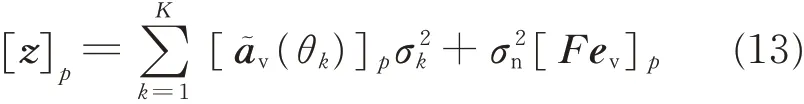
Remar k 2For example，in this paper，the number of physical sensors is selected at least N=10.According to Table 1 and Eq.（8），the generated consecutive virtual elements is 63，which is large enough for coarse DOA estimation by DFT method[11].

2.2 Fine DOA estimation by SS-MUSIC algorithm with partly spectr al search

Here，SS-MUSIC algorithm is exploited to obtain the fine DOA estimates.It should be noted that observation vector yvin Eq.（10）can be regarded as received signal of virtual consecutive array with(2M+1)elements located from-Md to Md.

According to Ref.[10]，the virtual array can be divided into M+1 overlapping subarrays and each subarray contains M+1 elements.The observation vector is denoted as yv，i，where i=1，2，…，M+1.yv，iconsists of the i th row to(i+M)th row of yv.The spatial smoothing function[10]can be constructed as

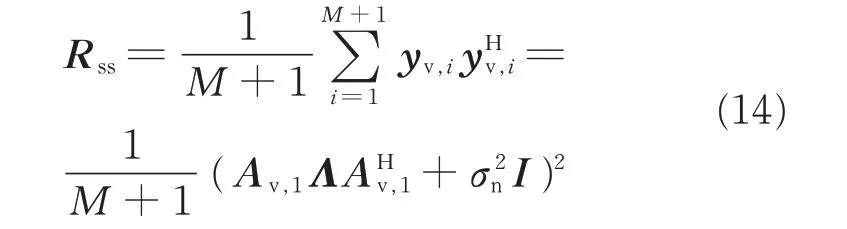
whereΛ=diag(σ21，σ22，…，σ2K)，Av，1is the direction matrix of observation vector yv，1and consists of the 1th row to(1+M)th row of Av.The k th column Av，1is presented as av，1(θk)=

It should be noted that Rssbehaves like the covariance matrix of signals received by a longer uniform linear array and hence MUSIC can be applied to Rss.The eigenvalue decomposition result of the covariance matrix Rsscan be denoted as[19]

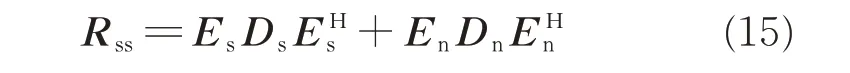
where Esand Enare the signal subspace and noise subspace matrices，respectively；Dsand Dncontain the eigenvalues.

According to the orthogonality between the noise and signal subspace，the spatial spectral function of MUSIC can be represented by[20]

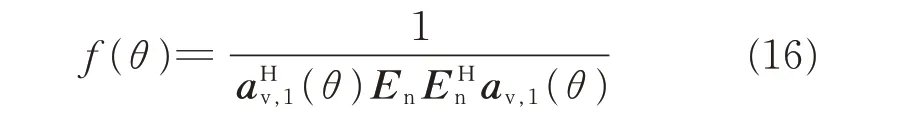
It should be noted that θcoak=arcsin[2pk/(2M+1)]can be obtained by DFT method in Section 2.1.Furthermore，pkis an integer. Therefore， after searching spectrum over θ∈{(θcoak-arcsin(1/(2M+1))， θcoak+arcsin(1/(2M+1)))|k=1，2，…，K}，fine DOA estimates ofθfinkcan be obtained in Eq.（16）.Compared with the traditional method by searching spectrum overθ∈(-90°，90°)，the proposed algorithm can reduce the computational burden.

The steps of the proposed algorithm are as follow.

Step 1Obtain the covariance matrix R of received signals x(t)，and subsequently vectorize R.

Step 2Select the observation vector yvof consecutive virtual array from vector y and compute the DFT yvin Eq.（13）.Subsequently，obtain the coarse DOA estimates.

Step 3Construct the spatial smoothing function as Eq.（14）and perform eigenvalue decomposition to covariance matrix Rssin Eq.（15）.

Step 4Construct spatial spectral function as Eq.（16）and search angles spectrum around the coarse estimatesθcoak.

Remar k 3In this paper，the number of impinging signals，which can be determined through locating the number of peaks of z by DFT method，should not be known in advance.

3 Performance Analysis

3.1 DOFs

Here，the consecutive DOFs for proposed array is 2N1N2+4N2+2N1-5.In Table 3 and Fig.3，the comparison of DOFs between the proposed array，two-level nested array[10]and Yang’s array[14]is provided under the same total number of physical sensors N，where the optimal sensors number of N1，N2are chosen using equations in Table 1 and some equations in Refs.[10，14]to maximize DOFs.

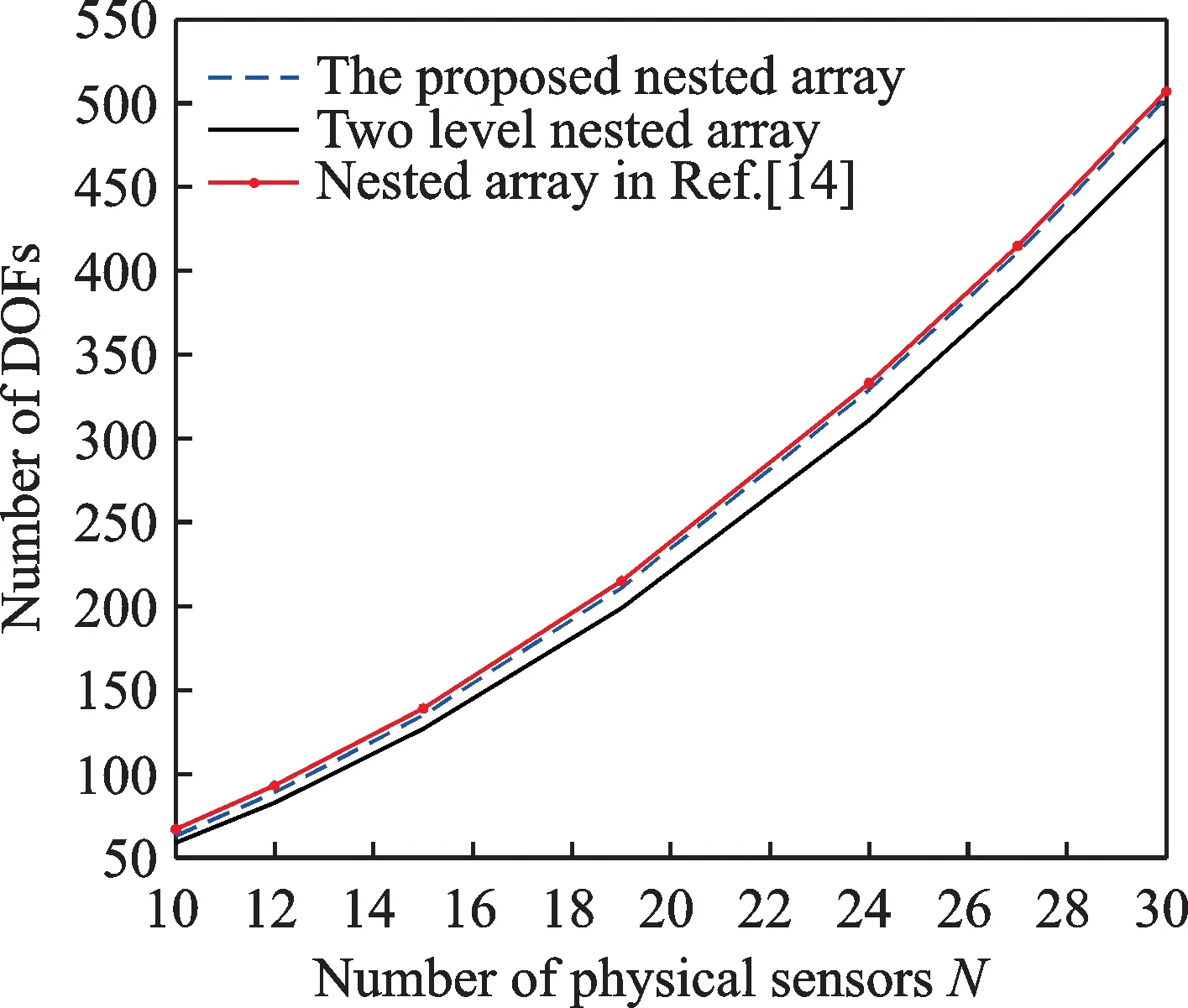
Fig.3 DOFs comparison versus the number of physical sensors

Table 3 Consecutive DOFs of different arrays

Fig.3 depicts that the proposed array has higher DOFs than two-level nested array.As basic discussion above，although the proposed array is slightly inferior to Yang’s array in DOFs，the proposed array enjoys the advantage of lower mutual coupling.Furthermore，the proposed array enables to achieve better DOA estimation performance than Yang’s array due to the more sparse structure of the first subarray，which will be verified by simulation results in the following.

3.2 Complexity

In this part，the complexity of the methods is evaluated by only computing the complex multiplication.Table 4 gives the comparison of complexity of proposed algorithm and traditional SS-MUSIC algorithm，where times of the global spectral search are set as Gpand Gt，respectively.As discussed above，coarse DOA estimates enable to make Gpfar less than Gt.Assuming that there exists two impinging signal withθ=[10°，50°]，the complexity of the proposed algorithm and traditional SS-MUSIC algorithm in Fig.4 is compared，where T=100，N=10，12，14，16 and the search stepΔ=0.01°.It can be seen from Fig.4 that the proposed algorithm can reduce the computational complexity.

Table 4 Complexity of differ ent methods

Fig.4 Complexity of methods versus number of sensors

3.3 Cr amer-Rao lower bound

The Cramer-Rao lower bound（CRLB）[21]is the lower bound of unbiased parameter estimation and is usually used as the performance comparison metrics.According to Ref.[22]，the CRLB of the improved nested array can be written as

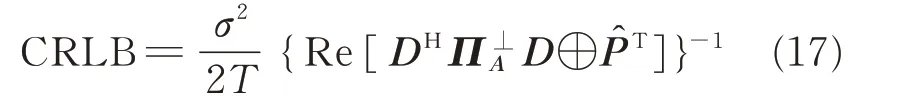
where D in Eq.（17）can be represented as[23]

Π⊥A=IN-A(AHA)-1AH， P^=?

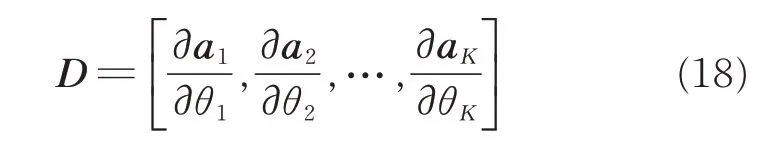
where akis the k th column of A，k=1，2，…，K.

3.4 Advantages

The improved nested linear array and the proposed DOA estimation algorithm have the following advantages：

（1）As compared to two-level nested array[10]，more available DOFs can be achieved by the improved nested array.

（2）The proposed algorithm enjoys the lower complexity than traditional SS-MUSIC algorithm.

（3）Estimation of the number of impinging signals is not required in advance by DFT method.

4 Simulation Results

In this section，extensive simulations are conducted for the improved nested array and the proposed algorithm.Assuming that there are K far-field narrow band independent signals impinging on the sensors array，the root mean square error（RMSE）is employed as the performance metric，which can be defined as

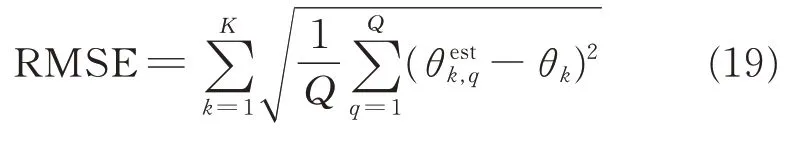
where Q is the number of Monte Carlo simulations andθestk，qis the estimate of the q th trial for the k th theoretical angleθk.And in this paper，Q is set to be 500.

4.1 RM SE per for mance comparison of different arrays

Here，the angle estimation performance and CRLB performance of different arrays are compared，which involve the two-level nested array[10]，the proposed nested array and the similar array configuration proposed in Ref.[14].

Compared with the nested array proposed in Ref.[14]，the proposed array enjoys the better DOA estimation performance due to the extended aperture of the dense subarray，which is verified in Figs.5 and 6，where T=500，θ=[10°，30°，50°]and N=10.Furthermore，both of the arrays described above have the better DOA estimation performance than two-level nested array.

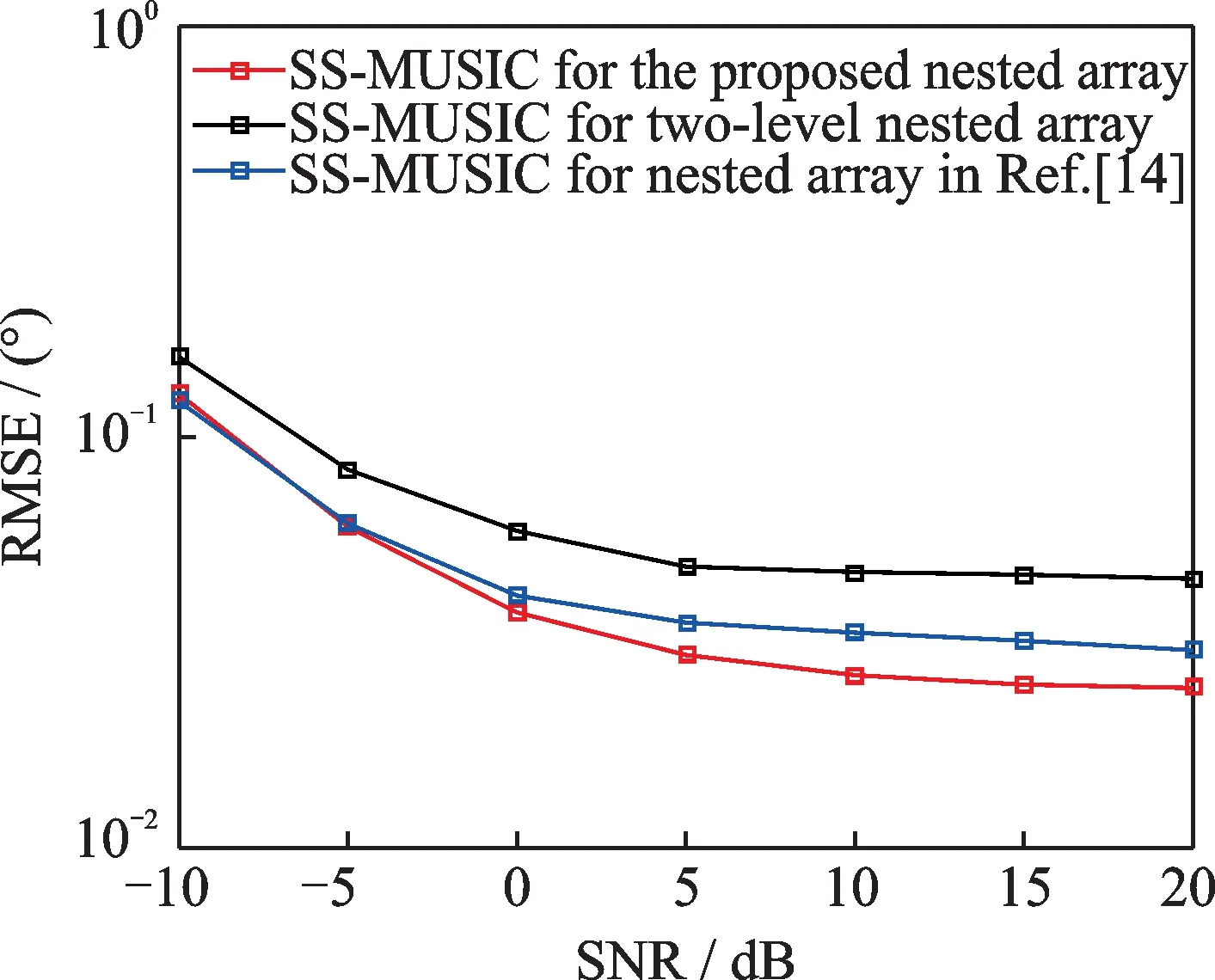
Fig.5 Angles estimation performance comparison of different arrays versus SNR

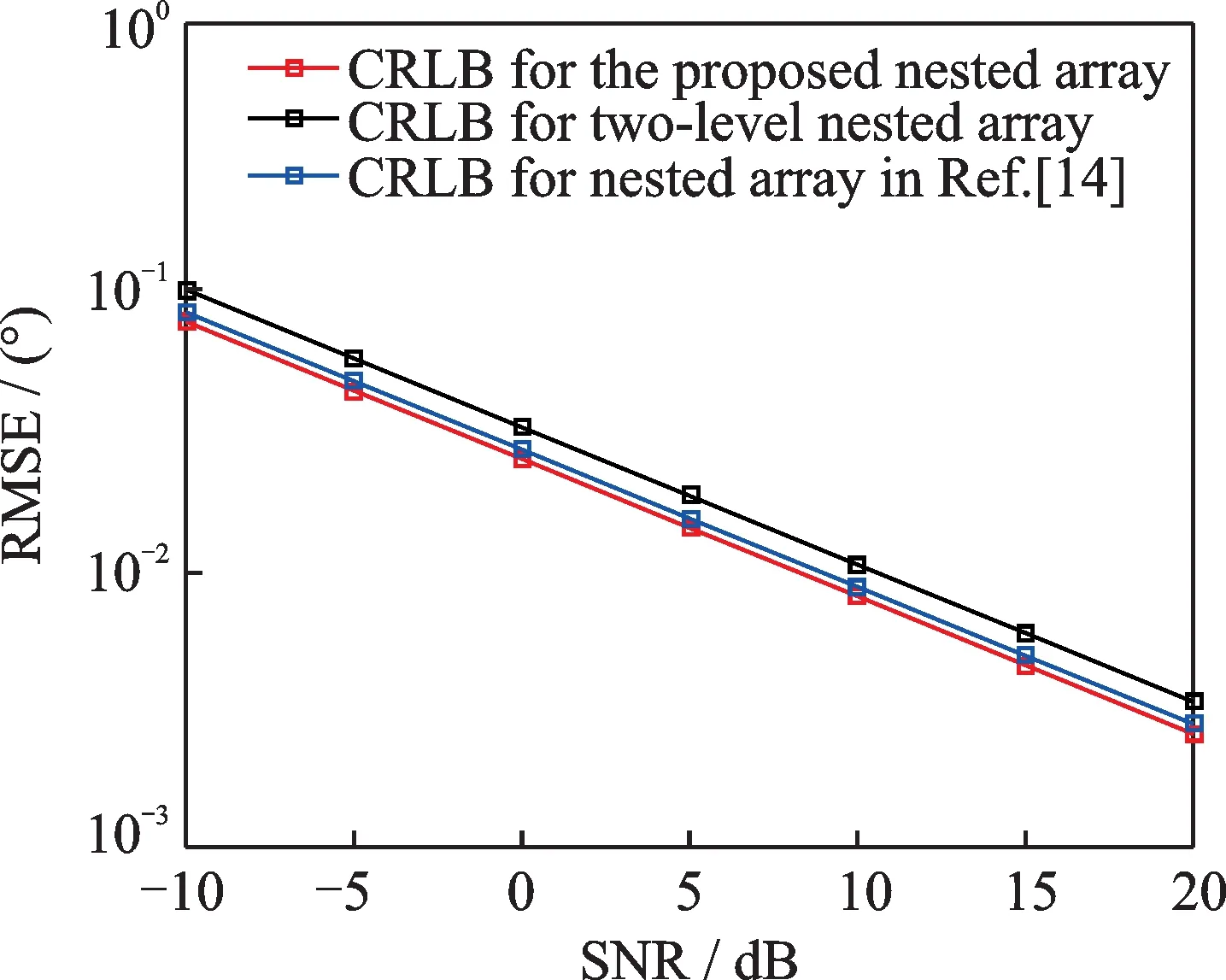
Fig.6 CRLB estimation performance comparison of different arrays versus SNR

4.2 RM SE perfor mance comparison of different algorithms

Fig.7 depicts the angles estimation performance comparison versus SNR of different algorithms with the proposed improved nested linear array，which involves SS-MUSIC algorithm[10]，proposed algorithm and the initial estimates obtained by DFT method，whereθ=[10°，30°，50°]，T=500 and N=10.

The proposed algorithm has the same estimation performance with SS-MUSIC algorithm.However，as mentioned in Section 3.2，the proposed algorithm enjoys the lower computational complexity.

Fig.7 Angles estimation performance comparison of different algorithms versus SNR

4.3 Comparison of RMSE performance versus different par ameter s

The angles estimation performance comparison of the proposed algorithm with different snapshots is shown in Fig.8，which indicates that the RMSE performance of the proposed algorithm can be improved with the increase of snapshots and SNR，whereθ=[10°，30°，50°]and N=10.

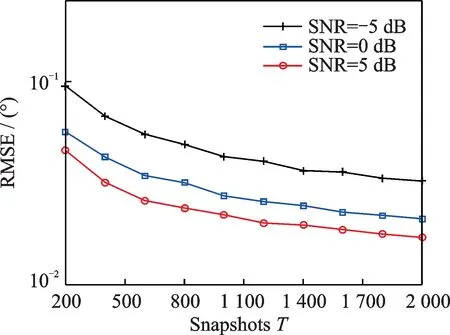
Fig.8 Angles estimation performance comparison versus different parameters

4 Conclusions

In this paper，an improved nested linear array is proposed，which can provide more DOFs and achieve better angle estimation performance than two-level nested array.Furthermore，to reduce the computational burden of SS-MUSIC algorithm，a computationally efficient DOA estimation algorithm is proposed with obtaining coarse DOA estimates by DFT method，which is utilized to shrink the rang of angle spectrum search of SS-MUSIC algorithm.