BeiDou B1I/B3I Signals Joint Tracking Algorithm Based on Kalman Filter

LYU Chade，ZENG Qingxi*，XU Rui，GAO Chang，QIU Wenqi

1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，P.R.China；

2.Key Laboratory of Nuclear Technology Application and Radiation Protection in Astronautics（Nanjing University of Aeronautics and Astronautics），Ministry of Industry and Information Technology，Nanjing 211106，P.R.China

Abstract:Dual-frequency satellite positioning receivers are widely used because they can eliminate ionospheric delay and solve the full-circumference ambiguity quickly.However，in traditional dual-frequency receivers，the relevance of dual-frequency signals are not considered，and，with no improvement imposed to the tracking loop，two independent tracking loops are used to achieve the tracking of dual-frequency signals.In this paper，the BeiDou dual-frequency signals joint tracking algorithm based on Kalman filter is proposed for the tracking of BeiDou B1I and B3I dualfrequency signals.Taking the relevance of B1I and B3I signals into consideration，the algorithm adds a Kalman filter between the phase detector and carrier loop filter of the traditional dual-frequency independent tracking loop.The output results of the phase detectors of the B1I and B3I branches are then combined and filtered by the Kalman filter，and the results are input to the carrier loop filters of the corresponding branches.Proved by experiments，the algorithm not only enables the loop to enter a stable tracking state quickly，but also reduces the noise bandwidth of the two loop filters by about 10 Hz with the same tracking performance obtained.

Key words:BeiDou;B1I/B3I;dual-frequency signals;joint tracking;Kalman filter

0 Introduction

Compared with single-frequency receivers，dual-frequency satellite positioning receivers are widely used in various precision navigation and positioning systems because they can eliminate ionospheric delay and solve the full-circumference ambiguity quickly[1].However，instead of taking the internal relevance of dual-frequency signals into consideration，the traditional dual-frequency receiver treats them as two independent signals and uses two independent tracking loops to achieve the tracking，thus the tracking loop can not get any improvement.

To address this problem，scholars around the world have endeavored to improve the traditional dual-frequency tracking loops，and proposed a series of new dual-frequency tracking algorithms based on the relevance of dual-frequency signals.In Ref.[2]，a method based on the relevance of L 1 and L 5 signals was proposed.By utilizing the carrier Doppler output of L 5 carrier loop to assist L 1 carrier tracking，this method effectively shortens the tracking time of the L 1 signal，improves the tracking sensitivity，and effectively reduces the dynamics of the carrier tracking loop of the L 1 signal.However，there is one critical problem：While the tracking loop of the L1 signal can obtain auxiliary information from the L 5 loop signal tracking，the L 5 signal tracking loop cannot obtain any auxiliary information from the L 1 signal tracking loop；erefore，once the L 5 signal is unlocked，the L 1 signal will also be unlocked[2].In Ref.[3]，a method based on combined Kalman filter，which replaces the traditional phase detector and loop filter，was proposed to track L 1 and L 5 signals.Utilizing the output of correlators to extract the tracking error for each loop，it obtains a smaller carrier phase error，and the loop bandwidth can accommodate changes in the scene.Moreover，an enhancement of 4 dB can be achieved in tracking sensitivity of the two signals compared to the individual tracking of each signal.However，the method model is too complicated and needs to be implemented on an embedded platform，In Ref.[4]，a method which utilizes receiver dynamics obtained by tracking and locating the L 1 signal to assist L 2 P（Y）code tracking was proposed.It greatly reduces the carrier-to-noise ratio of the traceable signal and the loop bandwidth by having the L 2 P（Y）code tracking loop neglect the effects of receiver dynamics.However，it will have a bad influence on the L 2 P（Y）tracking to utilize the tracking and positioning of the L 1 signal to assist when the L 1 carrier-to-noise is small.In addition，the scope of application is small as the method is for the tracking of the L 2 P（Y）specific signal，so it is not eligible to improve the tracking loop of other dual-frequency receivers.In Ref.[5]，a dual antenna joint carrier tracking loop was proposed for tracking global navigation satellite system（GNSS）carrier signals in signal-degraded environments.The tracking loop processes inputs from two antennas，namely，the master antenna and the slave antenna.The master antenna captures signals in open-sky environments，while the slave antenna captures signals in degraded environments.The Doppler frequency estimated by this master loop is utilized to assist weak carrier tracking in the slave loop.It can eliminate dynamic and clock noise in the slave loop and ensure that very narrow bandwidth is usable to suppress noise and improve tracking performance of weak signals[5].However，this method also has the common problem resulted from single-frequency assistance：The loss of lock in the main loop will inevitably cause the loss of lock in the slave loop.In Ref.[6]，a GNSS dual-frequency sum-diff joint tracking algorithm is proposed.It gives the tracking of L 1 and L 2 dual-frequency signals the same emphasis and realizes the mutual assistance of dual-frequency signals.The algorithm overcomes the inherent shortcomings of L 1-assisted L 2 algorithm effectively and improves the tracking robustness and sensitivity of dual-frequency signals.However，for a case where one of the dual-frequency signals is too poor，the algorithm will interfere the tracking of the other signal due to its coupling effect，and even cause the entire loop to be unlock[6].

In this paper，a BeiDou dual-frequency signals joint tracking algorithm based on Kalman filter is proposed for the tracking of BeiDou B1I and B3I dual-frequency signals.Based on the relevance of B1I and B3I signals，the algorithm adds a Kalman filter to the place between the phase detector and carrier loop filter of the traditional dual-frequency independent tracking loop.The output results of the phase detectors of the B1I and B3I branches are then combined and filtered by the Kalman filter，and the results are input to the carrier loop filters of the respective branches.The algorithm not only reduces the noise bandwidth of the two loop filters，weakens the dynamics of the loop and improves the tracking sensitivity，but also enabled the tracking loop to enter a stable tracking state quickly.

1 BeiDou B1I and B3I Signals

With primary completion and gradual improvement of the BeiDou-3 system（BDS-3），B1I and B3I signals are being broadcast on MEO satellites，IGSO satellites and GEO satellites of BDS-2 and BDS-3 to provide public services.The dual-frequency signals for the BeiDou dual-frequency receiver will also gradually transform from signals of B1 and B2 to signals of B1I and B3I.In February 2018，the China Satellite Navigation System Management Office officially released the modulation mode and signal structure of the BeiDou B3I signal.In February 2019，the original version of the spatial signal interface control file was upgraded，and the specific content of the B1I signal was redefined[7-8].

1.1 Structure of B1I and B3I signals

Both the BeiDou B1I and B3I signals are modulated by binary phase shift keying（BPSK），and are shown as in Eq.（1）and Eq.（2），respectively.The carrier frequency of the B1I signal is 1 561.098 MHz，and that of the B3I signal is 1 207.140 MHz.

where superscript j represents the satellite number；AB1Iand AB3Irepresent the amplitudes of B1I and B3I signals，respectively；CB1Iand CB3Ithe ranging codes of B1I and B3I signals，respectively；DB1Iand DB3Ithe data modulated on ranging codes of B1I and B3I signals，respectively；fB1and fB3the carrier frequencies of B1I and B3I signals，respectively；and φB1IandφB3Ithe carrier initial phases of B1I and B3I signals，respectively.

The difference between the B1I and B3I signals is mainly reflected in the ranging codes.The chip rate of CB1Iis 2.046 Mc/s，and the code length is 2 046 chips.The chip rate and code length of CB3Iare five times that of CB1I.The chip rate of CB3Iis 10.23 Mc/s，and the code length is 10 230 chips.Navigation messages of BeiDou signals are formatted in D1 and D2 based on their rates and structures.The rate of D1 navigation message which is modulated with 1 kb/s secondary code（NH code）is 50 b/s.D1 navigation message contains basic navigation information，while D2 navigation message contains basic navigation and wide area differential information and its rate is 500 b/s.The D1 navigation message is broadcast by the B1I signals of MEO/IGSO satellites.The D2 navigation message is broadcast by the B1Isignals of GEO satellites.

The NH code modulated on the D1 navigation message can enhance resistance to narrowband interference，reduce cross-correlation between satellite signals，and improve bit and symbol synchronization[9].The accuracy of the carrier tracking loop will be affected as the tracking loop must use a discriminator that is insensitive to data hopping due to the modulation of the NH code[10].

1.2 Relevance of B1I and B3I signals

For the BeiDou navigation satellite system，the B1I and B3I signals broadcast by the same satellite undergoing the same line-of-sight changes，so there is certain relevance between the Doppler shifts of the two signals.The carrier signal Doppler shift of the satellite signal generated by the relative motion of the receiver and the satellite is shown as

where fdis the carrier Doppler shift；fcthe satellite signal frequency；Δv the relative motion speed between the receiver and the satellite；vsthe speed of the satellite movement，and c the speed of light.When the satellite signals broadcast by the same satellite are received by the same receiver，theirΔv and vsare equal，and there is a relationship between the carrier Doppler shifts of the two signals，as shown in Eq.（4）

where fd1and fd3are Doppler shifts of B1I and B3I signals，and fB1and fB3carrier frequencies of B1I and B3I signals.

Eq.（4）is established in a completely ideal propagation environment，and the signal propagation in reality may be affected by factors such as ionospheric delay and multipath[11].However，it has been proved in Ref.[12]that the time delay caused by the ionosphere between the dual-frequency signals is small enough to be negligible.And this equation has been widely used in many studies on dualfrequency joint acquisition and tracking in the world[2-3，6，12].

2 BeiDou Dual-frequency Signals Joint Tracking Algorithm Based on Kalman Filter

Since Kalman filtering can well estimate and predict signal dynamics through a simple process and good filtering effect，it has been widely used in the design of carrier tracking loop and met the requirements of real-time signal tracking.

2.1 Dual-frequency signals joint tracking loop model

Fig.1 Principle of BeiDou dual-frequency signals joint tracking algorithm based on Kalman filter

The principle of the BeiDou dual-frequency signals joint tracking algorithm based on Kalman filter is shown in Fig.1.Based on the relevance of B1I and B3I signals，the algorithm adds a Kalman filter to the place between the phase detector and carrier loop filter of the traditional dual-frequency independent tracking loop.Since the Kalman filter has linear requirements for the system[13-14]，and the NH code modulation requires insensitivity of the phase detector to data hopping，the carrier loop phase detectors in the tracking loop used two-quadrant inverse tangent phase detectors.

Signals are processed like this.First，B1I and B3I intermediate frequency（IF）signals enter the carrier loop after code stripping.Second，the carrier phase errorsΔϕB1andΔϕB3output by carrier loop phase detectors of the B1 branch and the B3 branch（which are the loops that track B1I and B3I signals，respectively）are input into the Kalman filter as observations of the Kalman filter for filtering and estimating.Third，the estimated value of the output carrier phase errorsΔϕ′B1andΔϕ′B3are sent to the B1 and B3 branch carrier loop filters for filtering.Fourth，the control signals output by carrier loop filters control carrier NCO of each branch and generated fB1_NCOand fB3_NCOto adjust the frequencies of local carrier signals in real time，so as to be in consistency with the carrier frequencies of received signals.In this way，the closed-loop joint tracking of B1I and B3I dual-frequency signals is realized.

2.2 Design of Kalman filter

The Kalman filter model based on the relationship between two signal carrier frequencies and Doppler shifts is constructed.The system state vector is X=[ΔϕB1ΔϕB3fd，and the system measurement vector is Z=[ΔϕB1ΔϕB3]T，where ΔϕB1andΔϕB3are the carrier phase errors of the B1I and B3I branch carrier loop phase detectors respectively；fdand f˙dthe Doppler frequency and the change rate of Doppler frequency of the B1I signal，respectively.

The system state equation is

The system measurement equation is

The Kalman filter works as follows.

Step 1Parameter initialization.Initializeand P0.

Step 2Estimate the priori estimation state vector of the current momentthrough the posterior estimation state vector of the previous moment，and estimate the variance matrix of the priori estimation error at the current momentthrough the variance matrix of the posterior estimation error at the previous momentThe formulas are shown in Eq.（7）and Eq.（8）

where is the state transition matrix，Qk-1=E[] the process noise variance matrix，and E[·]the solving the covariance matrix.

Step 3Calculate the Kalman gain matrix Kkaccording to the variance matrix of the prior estimate error at the current moment.The formula is shown as

Step 4The state vector of the prior estimate at the current momentis corrected according to the Kalman gain matrix Kkand the current-time observation vector Zk，or in other words，the outputs of two carrier loop phase detectors，to get the posterior estimate of the state quantity at the current moment.At the same time，the variance matrix of the posterior estimation error at the current moment Pkis also obtained according to the Kalman gain matrix Kkand the variance matrix of the prior estimation error at the current momentThe specific formulas are shown as

where I represents a unit matrix of 4×4 order.

Step 5Use the formulato obtain the output values of the Kalman filter at the current moment，and input them to the B1 and B3 branch carrier loop filters.

Step 6Return to Step 2 and repeat the abovementioned operations to perform recursive calculations in sequence.

3 Experimental Verification and Analysis

The dual-frequency joint tracking algorithm based on Kalman filter was compared with the traditional dual-frequency independent tracking algorithm to verify its performance.The BDS-3 IF sampler was used to collect a set of BeiDou B1I and B3I IF signal data in the open area on the roof，and the IF signal data collection device is shown in Fig.2.After BeiDou signals were received through the antenna and input into the IF sampler to sample B1I and B3I frequency point signals，the sampled IF signal data were saved to PC through the serial port.The signal sampling frequency was 40 MHz，the center frequency of the BeiDou B1I IF signal was 0.098 MHz，and the center frequency of the BeiDou B3I IF signal was 0.52 MHz.The B1I and B3I signals collected by the IF sampler were stored in an interleaved mode，and a separate B1I or B3I signal can be obtained by reading data at intervals.

Fig.2 BeiDou B1I/B3IIF signal data collection device

Attempt was made to acquire B1I and B3I IF signal data prior to the tracking experiment and the 13th satellite was successfully acquired from each signal data，so the 13th satellite was tracked to verify the BeiDou dual-frequency signals joint tracking algorithm based on Kalman filter.It is worth mentioning that the 13th satellite is a medium earth orbit（MEO）satellite.The MEO satellite is the main component of the BDS-3 nominal space constellation，with high visibility on a global scale.According to acquisition results，the code phase of the B1I signal ranging code was at the 696th chip and the code phase of the B3I signal ranging code was at the 3 476th chip，and the Doppler frequency was-400 Hz，which were then used to initialize the tracking loop.

In addition，in order to evaluate the performance of signal tracking，the phase lock indicator（PLI）defined as[12]

where PLI（t）is the phase lock factor at time t；IPthe correlation value of the in-phase signal at the current time；QPthe correlation value of the quadrature phase signal at the current time；M the accumulated value，where 20 is taken.The PLI values will range from-1 to 1，and the closer the PLI value is to 1，the better the tracking effect of the loop is.It is generally considered that the most ideal tracking effect is achieved when the PLI value is greater than or equal to 0.995[15-16].

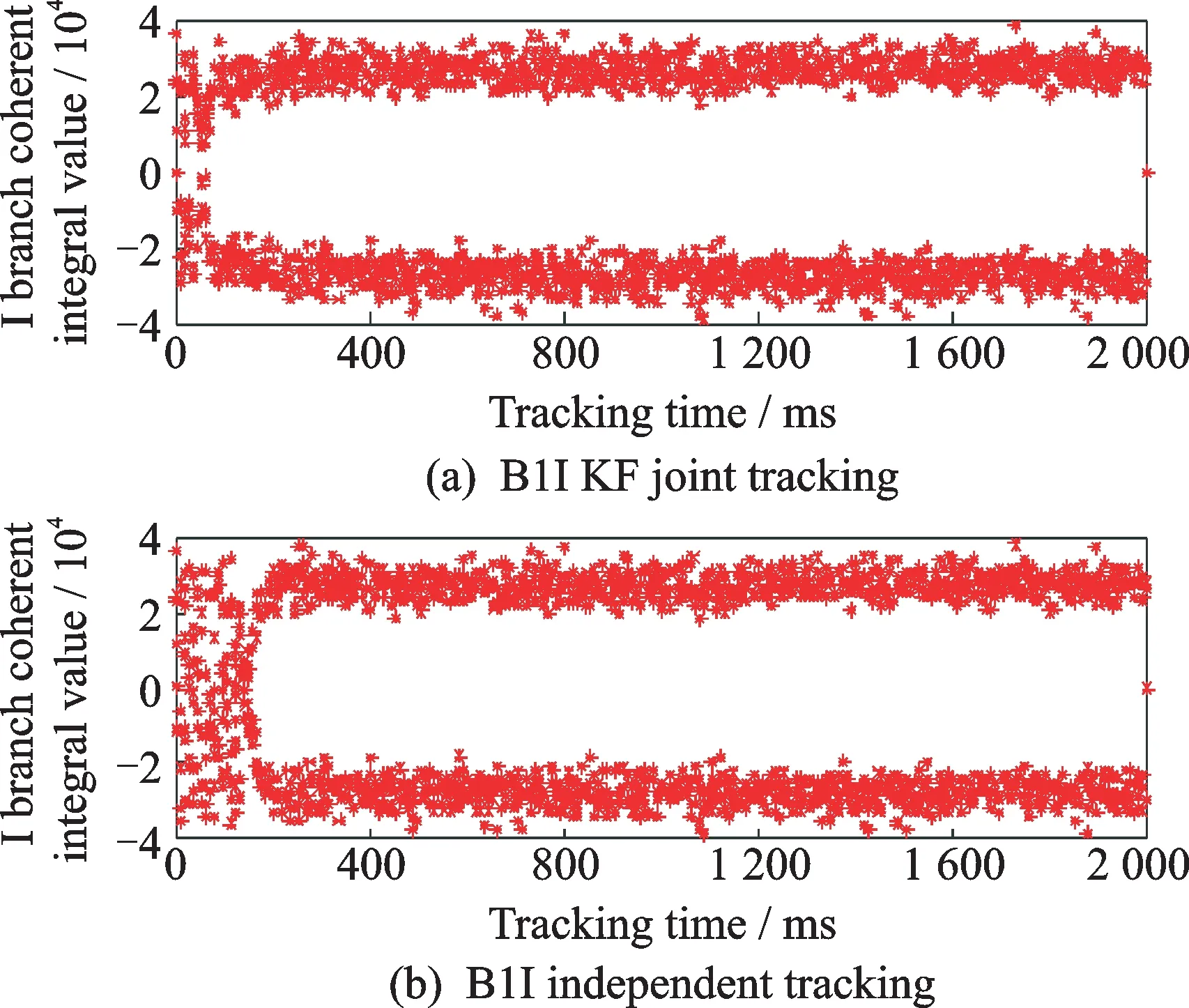
Fig.3 B1I signal I branch coherent integral values(B L=25 Hz)

Fig.4 B3I signal I branch coherent integral values(B L=25 Hz)

Fig.5 Comparison of carrier phase errors(B L=25 Hz)

Fig.6 Comparison of phase lock indicator(B L=25 Hz)

B1I and B3I signals were tracked using the two algorithms for 2 000 ms with the loop PLL（phase locked loop）noise bandwidth BLof the B1 and B3 branches set at 25 Hz，and the results are shown in Figs.3—6.In Figs.3，4，the I branch coherent integration values of B1I and B3I signals become stabilized in 60 ms and 70 ms，respectively，with the dual-frequency joint tracking based on Kalman filter，and the navigation message can then be demodulated，while those values tend to stabilize in 170 ms and 470 ms，respectively，with the dual-frequency independent tracking algorithm.Fig.5 is the comparison of the carrier phase errors of the two tracking algorithms.It can be seen that while the carrier phase errors of B1I and B3I signals with the dual-frequency joint tracking based on Kalman filter are greater than those with the dual-frequency independent tracking algorithm in the beginning，they are quickly adjusted to near zero and become stabilized with small fluctuations.Fig.6 is the comparison of phase lock indicators with the two tracking algorithms.It can be seen that it takes less time for the PLI values of B1I and B3I signals to get close to 1 with the dual-frequency joint tracking algorithm based on Kalman filtering.The above-mentioned results show that the tracking with the dual-frequency joint tracking algorithm based on Kalman filter come into stability faster than the dual-frequency independent tracking algorithm does.

With the loop PLL noise bandwidth BLof the B1 and B3 branches as 20 Hz，the tracking results are shown in Figs.7—10.In Figs.7，8，the I branch coherent integration values of B1I and B3I signals become stabilized in 100 ms and 140 ms，respectively，with the dual-frequency joint tracking based on Kalman filter，while those values tend to stabilize in 480 ms and 950 ms，respectively，with the dual-frequency independent tracking algorithm.It can be clearly seen from Figs.9，10 that the tracking with the dual-frequency joint tracking algorithm based on Kalman filtering come into stability faster.

Fig.7 B1I signal I branch coherent integral values(B L=20 Hz)

Fig.8 B3I signal I branch coherent integral values(B L=20 Hz)

Fig.9 Comparison of carrier phase errors(B L=20 Hz)

Fig.10 Comparison of phase lock indicators(B L=20 Hz)

With the loop PLL noise bandwidth BLof the B1 and B3 branches as 15 Hz，the tracking results are shown in Figs.11—14.In Figs.11，12，the I branch coherent integration values of B1I and B3I signals become stabilized in 180 ms and 250 ms，respectively，with the dual-frequency joint tracking based on Kalman filter.The I branch coherent integration value of the B1I signal tends to stabilize in 1 470 ms with the dual-frequency independent tracking algorithm，and the I branch coherent integration value of the B3I signal is distributed irregularly within 2 000 ms.Figs.13，14 show that compared with the dual-frequency joint tracking algorithm based on Kalman filter，the dual-frequency independent tracking algorithm takes much longer to track the B1I signal，and it even fails to achieve tracking lock of the B3I signal within the first 2 000 ms.Therefore，it is impossible for the dual-frequency independent tracking algorithm to complete the normal tracking of signals under the 15 Hz loop PLL noise bandwidth.

Fig.11 B1I signal I branch coherent integral values(B L=15 Hz)

Fig.12 B3I signal I branch coherent integral values(B L=15 Hz)

Fig.13 Comparison of carrier phase errors(B L=15 Hz)

Fig.14 Comparison of phase lock indicators(B L=15 Hz)

By comparing the tracking of signals under different noise bandwidths，we can see that the dualfrequency joint tracking algorithm based on Kalman filter simultaneously reduces the noise bandwidths of the two carrier loop filters，and the tracking performance is less affected in the case of reducing noise bandwidths，enabling quick stable tracking so as to realize navigation message demodulation.Under the same noise bandwidth，its tracking performance significantly outperforms the dual-frequency independent tracking algorithm to achieve stable tracking quickly.Moreover，by comparing the tracking results of the two algorithms under the 25 Hz and 15 Hz noise bandwidths，we find that the tracking performance of the dual-frequency joint tracking algorithm based on Kalman filter under the 15 Hz noise bandwidth is basically the same as that of the dual-frequency independent tracking algorithm under the 25 Hz noise bandwidth，and even better.Therefore，we can conclude that the loop noise bandwidth needed for the dual-frequency joint tracking algorithm based on Kalman filter can be reduced by about 10 Hz compared to the dual-frequency independent tracking algorithm with the same tracking performance obtained.

4 Conclusions

In this paper，based on the relevance of B1I and B3I signals，a BeiDou dual-frequency signals joint tracking algorithm based on Kalman filter is proposed by improving the carrier tracking loop of the traditional dual-frequency receiver.The experimental results show that the algorithm reduces the noise bandwidths of the two carrier loop filters at the same time through estimating the carrier phase error of the two phase detectors with the Kalman filter，thus reducing the dynamics of the loop and improving tracking sensitivity and stability.Compared with the dual-frequency independent tracking algorithm，the loop noise bandwidth of the dual-frequency joint tracking algorithm based on Kalman filter is reduced by about 10 Hz with the same tracking performance obtained.Moreover，the proposed algorithm has better tracking performance，and enters a stable tracking state faster.It will effectively improve the tracking performance of dual-frequency receivers for dual-frequency signals if applied to a dualfrequency receiver.