Modeling and Characteristic Analysis of Visco-Hyperelastic Film Based on Biaxial Tensile Experiment
2019-03-07ZHAOHaifengZHANGYaLIShizhongLUOHuaan
ZHAO Haifeng,ZHANG Ya,LIShizhong,LUO Huaan
1.Faculty of Mechanical and Electrical Engineering,Nanjing Vocational College of Information Technology,Nanjing 210023,P.R.China;
2.Faculty of Mechanical and Electrical Engineering,North University of China,Taiyuan 030051,P.R.China
Abstract:Dielectric elastomers(DEs)show complex mechanical behaviors with different boundary conditions,geometry sizes,and prestress.In this study,a three-component linear visco-hyperelastic model of DE film is developed based on equibiaxial tension.By applying hereditary integrals to analyze multiple-segment loading processesof film stretching,the model parameters are extracted by fitting the visco-hyperelastic film model to the experimental data.To demonstrate the performance of proposed model,the obtained predictive results are compared with the experimental results under different equibiaxial loading conditions.The good agreement between them shows that the linear visco-hyperelastic model is a promising tool for analytically investigating the property of pre-stretched DE actuators.Finally,the Prony series coefficients are calculated according to the relaxation function.This is helpful for simulation analysis using commercial finite element software.
Key words:dielectric elastomers;equibiaxial tension;Prony series;visco-hyperelastic
0 Introduction
Among the deformable electroactive polymers(EAPs),dielectric elastomers(DEs)show impressive expansibility when activated at high voltages,which makes them be used as actuators in adaptive structures[1-2].And DEs have been extensively studied in robots,machine insects,artificial limbs,artificial manipulators and other high-tech research fields in recent years[3-6].Acrylic rubber is an electroactive polymer with viscoelasticity and superelasticity,which is often used as dielectric elastomer actuator.In this study,a visco-hyperelastic film model of an acrylicrubber is evaluated,e.g.,VHB4910 from 3M,which has been widely used in DE actuators.
The constitutive model is a mathematical expression reflecting macroscopic properties of materials.It is very important to study the constitutive model of dielectric elastic materials for designing and optimizing DE actuators.In the early publications about linear elastic materials,the visco-hyperelastic behavior of DEs was seldom involved.The large strain elastic response of elastomer was often modeled by using the strain energy function such as Mooney-Rivlin,Yeoh,and Ogden forms.Simultaneously,the time-dependent functions such as Prony series were used to describe the viscosity[7-8].Hart-Smith reported exponential-hyperbolic elasticity parameters for rubber-like materials over full range of deformations based on the inflation of spherical balloons[9]and provided the numerical solutions for the problem of inflation of a circular membrane[10].Guggi Kofod described several elastic models for polymer materials and discussed their discrepancies in different strain ranges[11].
In DE actuators,DE is usually subjected to Maxwell compressive pressure,which is similar to an equibiaxial tensile stress state.Pure shear geometry[12-13]and uniaxially stretched dielectric actuators[14-20]are effective methods to evaluate timedependent behavior and other characteristics of DE actuators.However,the above mentioned methods are not very suitable for the analysis pre-stretched film actuators[21].Zou et al.[22]studied hysteresis mechanical model of spring metal-net rubber combination damper.Huang et al.[23]reported an anisotropic visco-hyperelastic constitution model for cordrubber.Tan et al.[24]proposed a transversely isotropic visco-hyperelastic constitutive model for short fiber feinforced EPDM.Wang[25]studied the viscoelastic behavior of a circular dielectric elastomer film actuator under electromechanical coupling.Chen et al.[26]discussed a hyperelastic constitutive model for membrane and its application in air cushion.David et al.[27]presented the governing equations for the electromechanically coupled behavior of dielectric elastomers in a thermodynamic framework and discussed the attendant finite-element formulation and implementation by using a commercial finite-element code.Although many hyperelastic constitutive models describing polymers have been proposed by researchers at home and abroad,little research has been done on the visco-hyperelastic deformation of acrylate rubber.
In this study,a visco-hyperelastic model of dielectric elastomer acrylic rubber film is proposed based on an equibiaxial tensile experiment.By applying hereditary integrals to analyze multiplesegment loading processes of film stretching,the model parameters are extracted by fitting the viscohyperelastic film model to the experimental data.The mechanical response of visco-hyperelastic film is expressed using a three-component model.Then hereditary integrals are applied to analyze multiplesegment loading experiment,and the model parameters are extracted by fitting with the equibiaxial experimental data.The mechanical responses under different loadings are also predicted and compared with the experimental data.The Prony series coefficients are calculated using the model parameters.And some conclusions of this study are provided.The linear visco-hyperelastic model can be used to evaluate the property of equibiaxially pre-stretched DE actuators.
1 Visco-Hyperelastic Model for Square Film
First,the proposed model does not provide a general description of visco-hyperelastic polymers.It can serve as a tool to analyze the characteristics of DE actuators.Because Maxwell and Voigt models describe only the relaxation and creep characteristics,respectively[21],the multi-component model is used to describe the actual visco-hyperelastic model,which should be nondegenerate.
Basically,it is helpful to assume that the model of film is composed of countless microcubes with the same cross-sectional area and the length,as shown in Fig.1(a).Each segment of the cube consists of two springs and one dashpot,as shown in Fig.1(b).
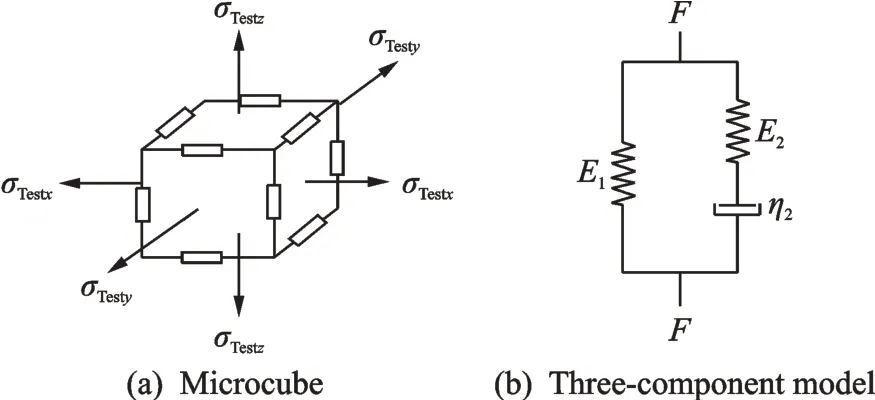
Fig.1 Schematic of linear visco-hyperelastic model
To simplify the analysis,the following conditions are required for the model.
(1)Visco-hyperelastic material is an isotropic and homogeneous medium.
(2)The central zone of film in the equibiaxial tensile experiment is uniformly subjected to contraction or elongation deformation,i.e.,by neglecting the shear effect.
(3)Visco-hyperelastic film is incompressible.
Other assumptions such as mass-free,cuboid geometry maintained under deformation[14]are also required.
In this study,as is shown in Fig.1(b),a threecomponent model is used,in which a spring is linked with a dashpot and two components are linked with another spring in parallel(i.e.,the Kelvin model).Here E1and E2are the stiffnesses which are defined by ki/s(0),i=1,2,where s(0)is the original length of segment and kiis the stiffness coefficient of spring in Fig.1(b).Andη2is damping coefficient which is defined by d/s(0),where d is the damping coefficient of dashpot.As the approximation,it is assumed that the cube consisting of a spring-dashpot is filled with incompressible fluid,and the hydrostatic pressure varies with the deformation of the cube.E1,E2,andη2in the spring-dashpot system are also assumed to be constant,and σTesti(i=x,y and z)are external normal stress of the cube.
In the above mentioned model,the spring is the linear-elastic component,and the dashpot is the viscous component.In the model,the stress of each component is equal,and the total strain is the sum of individual strains in series connection.The total stress is the sum of stress in each link,and the strain in each link is equal in the parallel connection.As shown in Fig.1(b),when the external force F(t)is applied,the force equilibrium results in a differential equation for the deformation behavior in three directions,which is
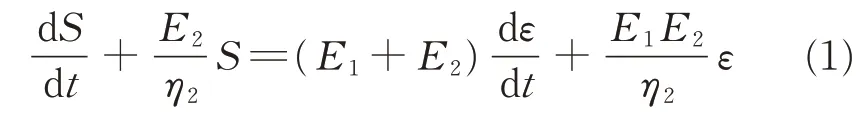
where the stress is defined by S=F/(s(0))2.F is the external force,dε/d t the deformation rate,andεthe strain.When the step strainε(t)=ε0H(t)is applied to the model,the relaxation stress formula can be obtained by solving Eq.(1).
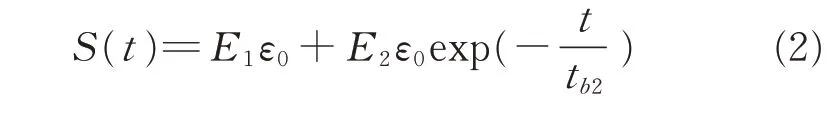
where tb2=η2/E2is the retardation time.Therefore,the relaxation function E(t)can be expressed as
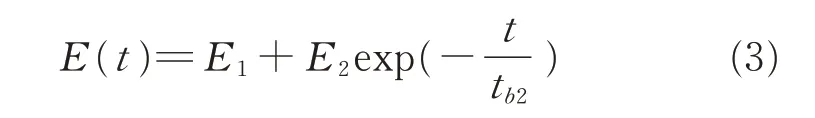
When equibiaxially stretched,the film is extended in the x,y directions and contracted in the z direction.The external normal stress ofσTesti(i=x,y,and z)can be expressed by
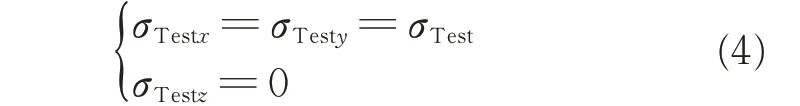
During the deformation,the internal hydrostatic pressure p(t)diverges from zero.The force equilibria across the wall of deformed cuboid results in[12]
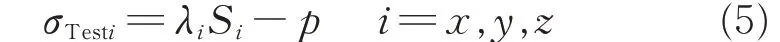
whereλiare the stretch ratios.The stretch ratios λi=are the ratios of the deformed dimension to the original dimension of the film.
2 Equibiaxial Tensile Experimental Analysis
The parameters of the visco-hyperelastic model can be derived from the experimental data,and then the performance of the dielectric actuator can be analyzed.The experiments include creep,relaxation,constant rate stress,constant rate strain and dynamic measurement[28].
In this study,the visco-hyperelastic model is analyzed by designing an equibiaxial tensile experiment apparatus.The working principle of the equibiaxial tensile experiment is shown in Fig.2.Two stepping motors(not shown in the Fig.2.)drive two pairs of reverse screw rods to rotate.Thus,two pairs of slideways of X and Y axes are drived to move equibaxially symmetrically along X and Y directions respectively.The specimens are clamped by 20 self-tightening clamps with uniform distribution around them.In the center of specimen,four dark orthogonal markers are printed for measuring the displacement.The experimental specimens are in the form of square sheets,which are 9 cm long on each side and 1 mm thick.Two load cells are mounted on the two sides of slideway.While stretching symmetrically,the bearings on the back of self-tightening collets slide along the slideway almost simultaneously.The strain of the sample can be measured by the caliper and the tension can be collected by force sensor.Fig.3 is the design of the equibiaxial tension experiment apparatus.
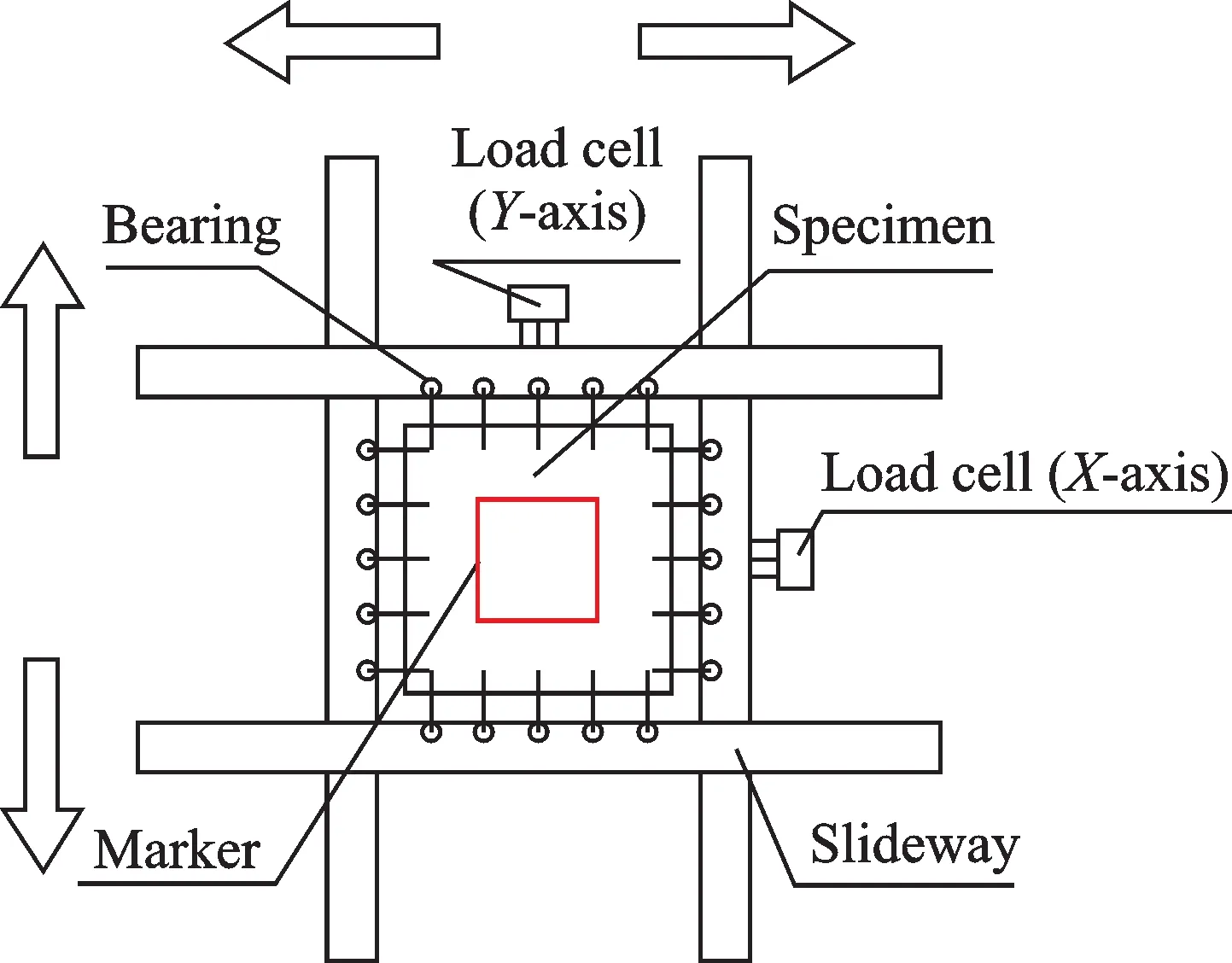
Fig.2 Principle of equibiaxial tension experiment

Fig.3 Equibiaxial tension experiment apparatus
2.1 Multiple-segment loading process
In the tension,the ideal creep and relaxation experiments cannot be satisfied,so the model parameters are obtained by multiple-segment loading on the biaxial experiment apparatus at approximately constant tension rate[29-30].
Under equibiaxial tension condition,according to the incompressibility(λxλyλz=1),the following equations can be formulated.
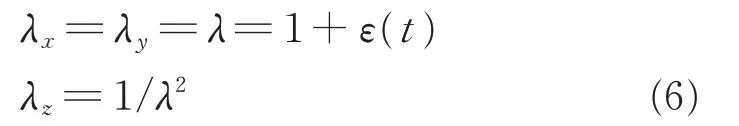
It is observed that the deformation in z-axis direction is different from that in x and y axes directions.The equibiaxial multiple-segment loading processes are shown in Fig.4,which can be divided into three segments.Firstly,the film samples are equibiaxial stretched at a tensile rate of 3.54e-3,then maintained 900 s,and finally regressed at the same rate.
The strain rate functions in x,y axes directions are defined as
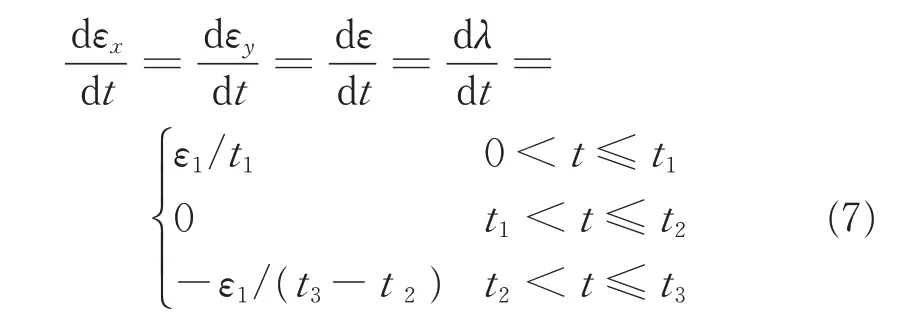
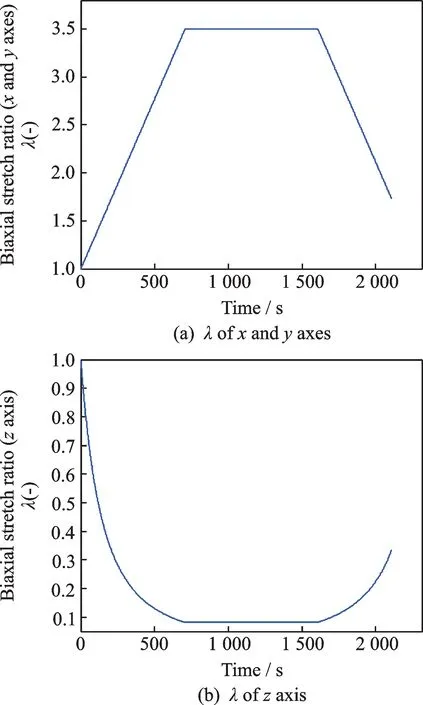
Fig.4 Equibiaxial multiple-segment loading processes
Owing to the incompressibility,the straining rate in z axis is not constant.To facilitate the subsequent analysis,the stretch ratio in z axis can be expressed with 4th degree polynomial inλin the first and third segments.According to the defined stretch ratio of equibiaxial tensile experiment,where the stretch ratio isλ=3.5,the polynomial can be fitted with Matlab(see Eq.(8),the fitting range is up to λ=4).Then the strain rate in z-axis direction can be obtained by differentiating the stretch ratioλzwith respect to time t(see Eq.(9)).
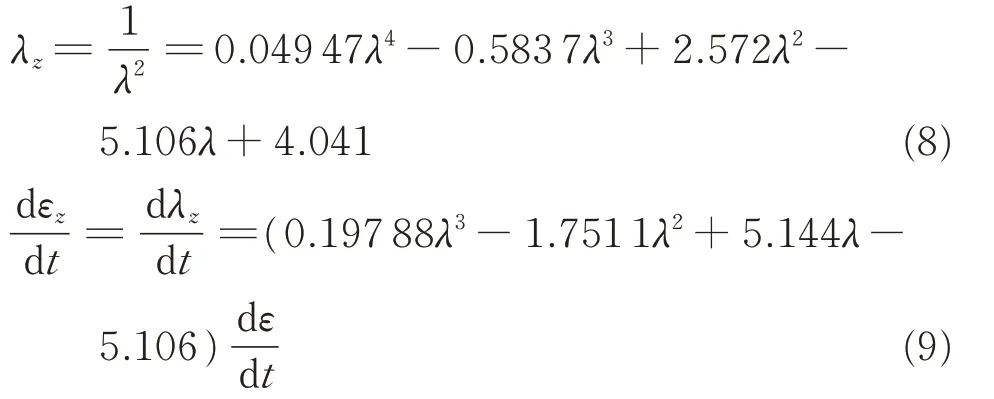
Substituting Eqs.(6,7)into Eq.(9),different strain rates of three segments in z-axis direction can be obtained.
2.2 Application of hereditary integrals to multiple loading pr ocess
To determine the stress in a visco-hyperelastic material at a given time,the deformation history should be considered.For a linear visco-hyperelastic material,a superposition of hereditary integrals can be used to describe the time-dependent response.According to the relaxation function,the stress equation in the film model can be expressed as
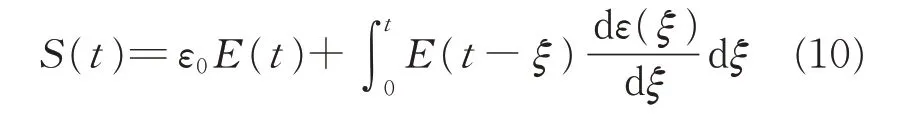
In equibiaxial multiple-segment loading processes,withε0=ε(0)=0,the stress functions in each segment can be shown as follows.
Step 1By equibiaxially stretching the square film(0<t≤t1),the stress response depends on the imposed constant-rate straining as
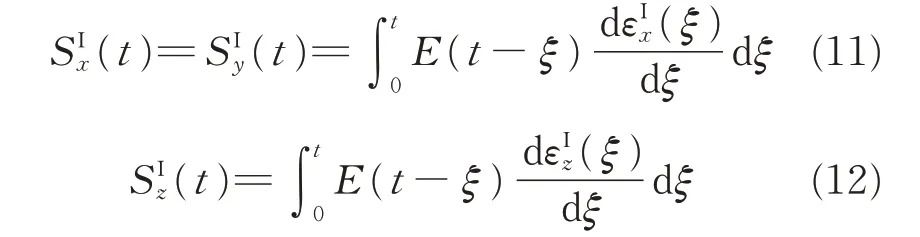
where index I represents Step 1.Note that under the deformation,the internal hydrostatic pressure of p(t)changes simultaneously.Therefore,Solving Eqs.(11—14)and substitutingλIz=(λI)-2into the results yield
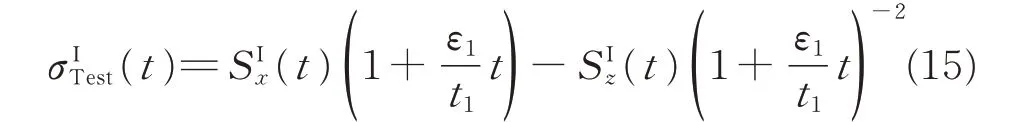
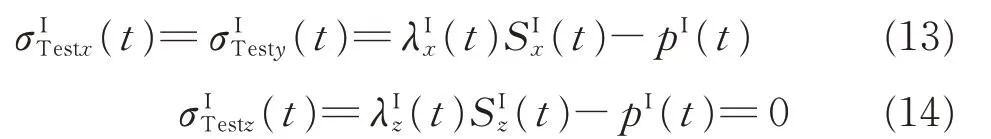
Step 2Relaxation(t1<t≤t2).Using the first and second strain ingrates yields
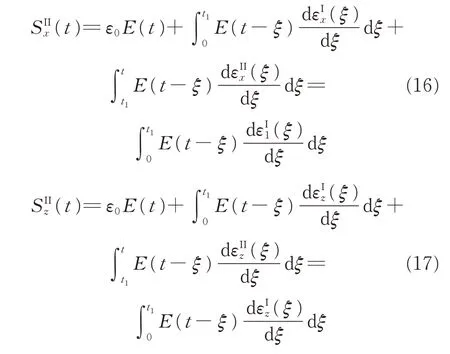
where index II represents step2.Considering the internal hydrostatic pressure of p(t),the tensile stress can be derived as Step 3 Regression(t2<t≤t3).The stress responses to the imposed constant-rate straining-ε1/(t3-t2)are as follows.
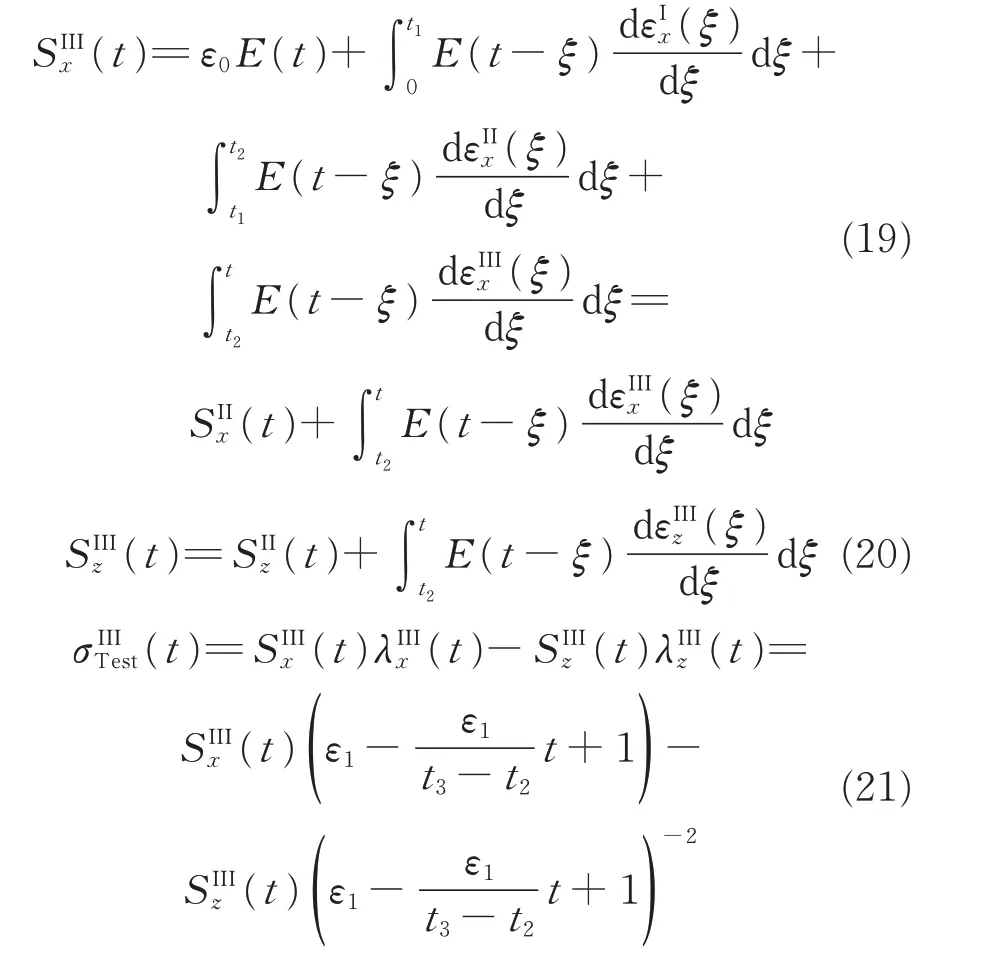
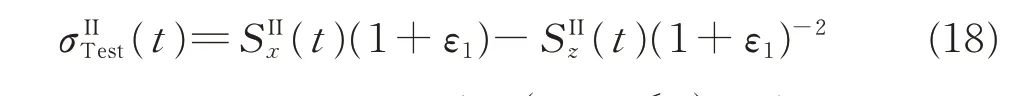
where indexⅢrepresents step 3.
2.3 Fitting of visco-hyperelastic film model
The VHB4910 double-sided adhesive manufactured by 3M Company has been tested by multiplesegment tensile experiment on equibiaxial tension apparatus.The experimental data are shown in Fig.5(a).By fitting Eqs.(15,18,21)to the experimental data,the model parameters(E1,E2andη2)can be obtained.To optimize the parameters,another equibiaxial tension experiment is applied to the same specimen,whose experimental data are shown in Fig.5(b).By fitting and synthesizing the two experimental results,the final parameters are as follows:E1=0.021 N·mm-2,E2=0.017 N·mm-2,andη2=1.75 N·s·mm-2.
The two experimental specifications are shown in Table 1.
Experiment 1 shows that the predicted model agrees well with the experimental data when the tension rate and relaxation rate are the same.Experiment 2 shows that experimental data are also in good agreement with the fitting model when the tensile ratio and regression ratio are quite different.
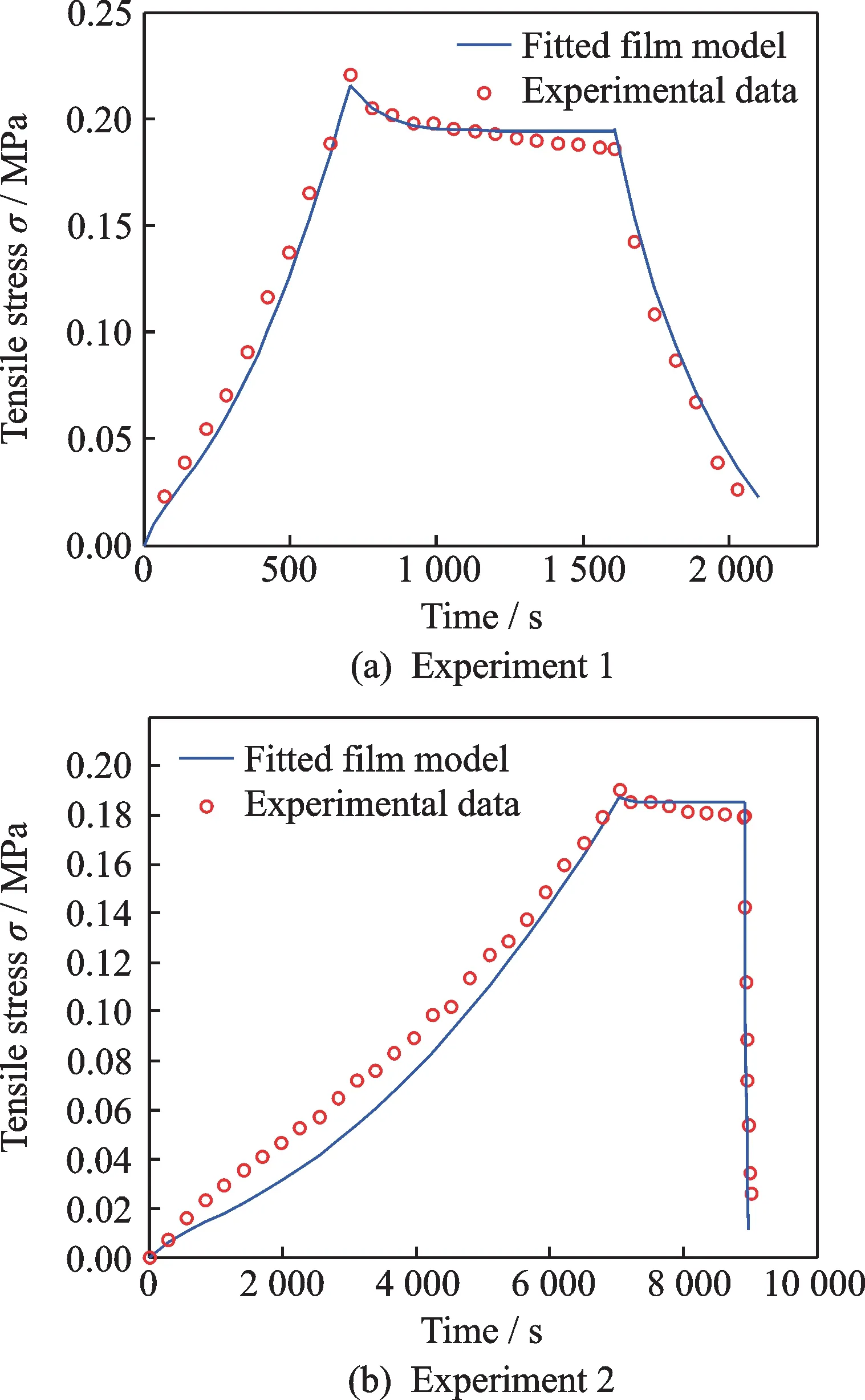
Fig.5 Fitting of visco-hyperelastic film model

Table 1 Experimental specification
After obtaining the visco-hyperelastic model parameters,the different stress response curves at different stretch rates and stretch ratios can be predicted.The predicted stress response curves at different stretch rates are shown in Fig.6 whenλ=3.5.The predicted stress response curves at different stretch ratios are shown in Fig.7 whenλ.=1.77e-2 s-1.The predicted results show that the tensile rate affects the maximum response stress,and the tensile ratio determines the quasi-static stress.Simultaneously,the predicted results(fitted film model(—))are compared with the experimental data(○),and the results show that both agree well within the experimental range.The deviation is observed when the stretch ratios are low(either during stretching or relaxation).The error is related to the accuracy of the experiment itself.In addition,the tensile-relaxation experiment is carried out by means of square uniform point clamping method.The film deformation at clamping position and non-clamping position is not uniform.In the case of small tensile ratio,the non-linear characteristics of deformation are particularly prominent,which results in the deviation of experimental stress from the fitting ones.Eliminating above factors,the fitting stress curve of the film is basically consistent with the experimental data,and the trend and smoothness of the curve are very similar,which shows that the visco-hyperelastic model is effective.

Fig.6 Stress response curves at different stretch rates when λ=3.5
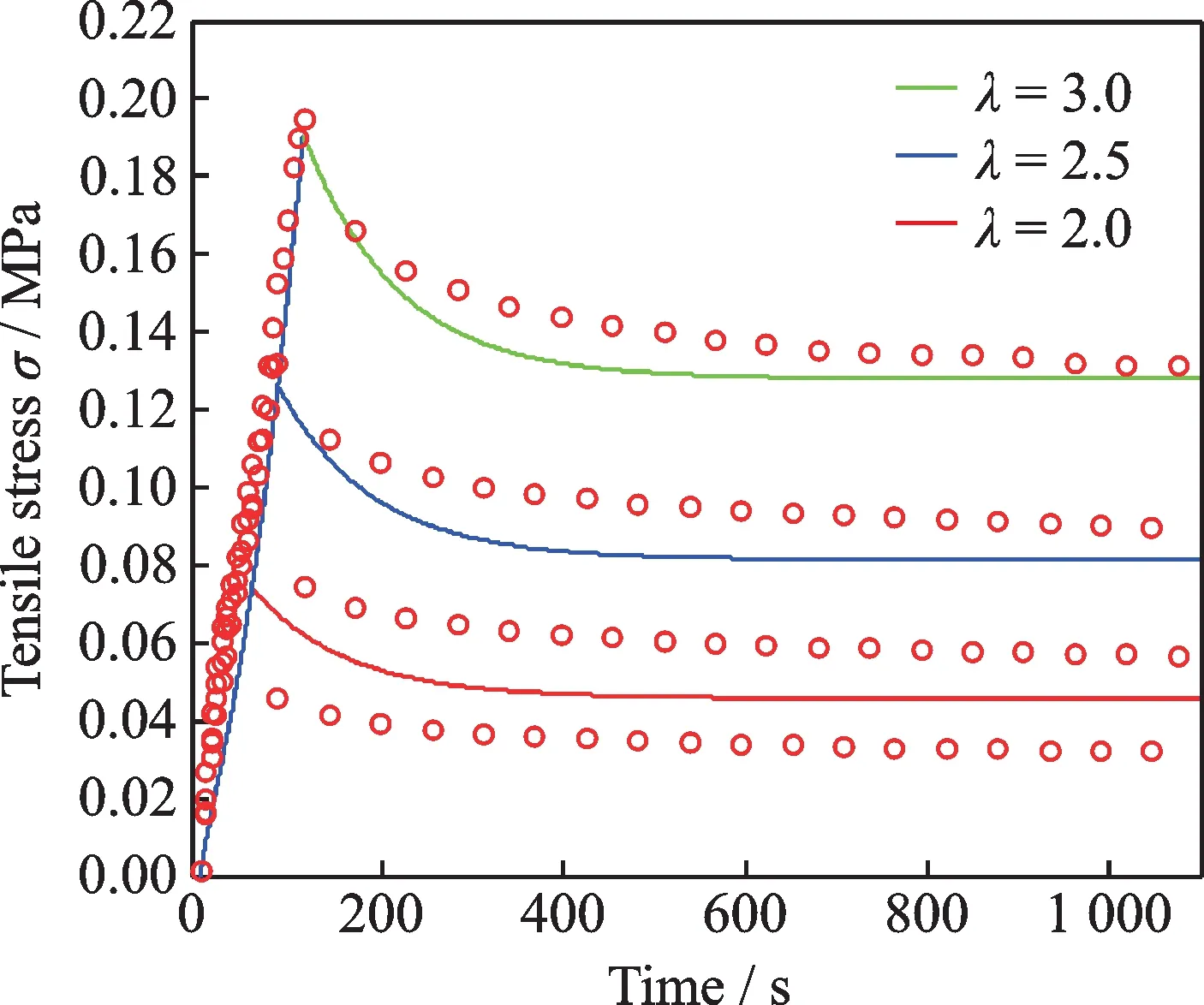
Fig.7 Stress response curves at different stretch ratios when λ˙=1.77e-2 s-1
3 Deduction of Prony Series Coefficients
The visco-hyperelastic model based on strain energy is an effective method for describing the quasilinear visco-hyperelastic of materials.In most finite element packages,the linear visco-hyperelastic model is specified by a relaxation function of Prony series.Thevisco-hyperelastic material parameterin strain energy potential can be expressed as[7]
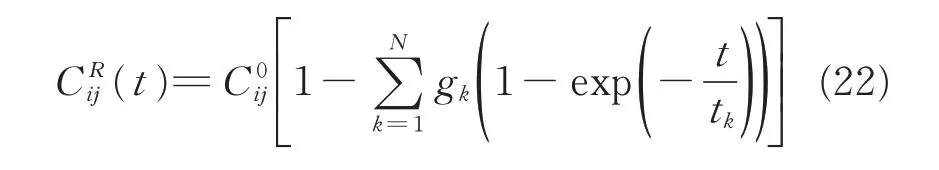
where C0ijis the instantaneous elastic response,and gkand tkcharacterize the relaxation behavior.
Generally,the assumption of quasi-linear viscoelasticity is that the stress relaxation function is independent of the magnitude of deformation.This can be verified by equibiaxial relaxation experiment sunder different stretch ratios.Fast manual experiments are performed on a biaxial experiment apparatus by equibiaxially stretching the square films quickly(0.2—0.5 s)to a predefined elongation(λ=2.5,2,1.5),then fixing the sample with a special fixture to relax.The relaxation force is sampled from the force sensor along X and Y axes,and the average values of X and Y axes data are obtained(Fig.8).The nominal stress S after long relaxation(1 500 s)is normalized.
It can be seen from Fig.9 that several normalized relaxation curves are very close to each other,which can verify the quasi-linear hypothesis.
Means of normalized experimental curves are also used to compare with other analytical results(see Fig.10).
Based on the relaxation function shown in Eq.(3),the Prony series coefficients can be calculated.Under equibiaxial relaxation condition,by normalizing relaxation stress S(t)(i.e.,Eq.(2))and Prony series,the following formulations can be deduced.
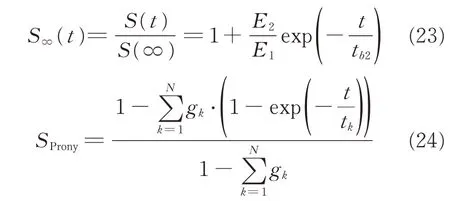
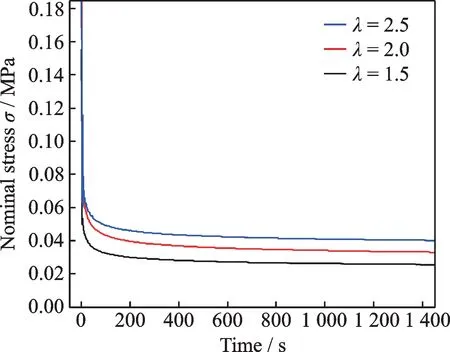
Fig.8 Nominal stress versus time at different elongations

Fig.9 Normalized nominal stress from different experiments

Fig.10 Comparison of different normalized stress and Prony series
Comparing Eq.(23)with Eq.(24),one-term Prony series coefficients can be obtained.By solving Eq.(25),the final results are as follows:g1=0.447,t1=102.9.Fig.10 shows a comparison of different normalized stress and Prony series.The deviation occurs at the beginning of relaxation period.The reasons lie in:(1)When rapidly stretching the film,the viscous effect is significant and thus the stress is tremendous;(2)There is a gap between the ideal step deformation and the manual rapid tension rate,so the initial stress value cannot be given accurately.It can be concluded that the visco-hyperelastic model mentioned above is adequate for quasi-static analysis.
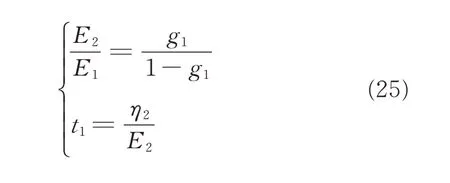
4 Conclusions
A three-component visco-hyperelastic model can be used to describe the time-dependent mechanical response of avisco-hyperelastic film under equibiaxial tensile condition.The model parameters can be extracted through equibiaxial multiple loading experiments.The relationship between model parameters and one-term Prony series can be deduced through the normalization.The results show that the analysis and experiment agree well,providing the evidence for the evaluation of subsequent equibiaxially pre-stretched DE actuators.Finally,when using linear visco-hyperelastic model in practical application,appropriate working conditions and stretching range should be considered.The effect of tensile ratio on model parameters needs further study.
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- BeiDou B1I/B3I Signals Joint Tracking Algorithm Based on Kalman Filter
- Impact Analysis of Solar Irradiance Change on Precision Orbit Determination of Navigation Satellites
- Characterization of Self-driven Cascode-Configuration Synchronous Rectifiers
- Cooperative Search of UAV Swarm Based on Ant Colony Optimization with Artificial Potential Field
- H∞Preview Control for Automatic Carrier Landing
- Single-Phase to Three-Phase Inverter with Small DC-Link Capacitor for Motor Drive System
