航空公司机上周转品多基地库存优化模型
2019-03-07宋江海高敏刚
宋江海,池 宏,高敏刚
(1.中国科学院科技战略咨询研究院,北京 100190;2.中国科学院大学,北京 100049)
1 引言
随着高铁的普及、电子商务的飞速发展,使得航空公司的竞争日益激烈,成本控制成为航空公司增强市场竞争力的关键,加强对各项运营成本的控制显得尤为重要。
机上周转品是航空公司为旅客提供的且能进行反复清洗回收使用的餐食用品及用具、盥洗用品及用具,如瓷器、玻璃制品、餐车、毛巾等。大型的航空公司为保障生产运营,一般在多个重要机场设有基地(或分公司)。由于往返航班配备的机上周转品数量不同,容易导致一些基地仓库出现积压而另一些基地仓库产生短缺;加之,对整个机上周转品的库存系统缺乏有效的信息共享及调运机制,使得机上周转品的订货成本一直居高不下。
目前民航领域关于机上周转品的研究相对较少,并且缺乏定量的模型分析。赵桂红和马志刚[1]针对机供品的组成、特点以及在成本控制方面存在的问题,提出了不同类型的机供品成本控制的解决方案。谷伟强[2]以某航空公司自主开发的“机供品管理平台”为例,分析了机供品管理信息系统的设计与实现的全过程。
与机上周转品类似的物品有托盘、集装箱等,那么关于此类物品的研究大多集中在如何进行调度方面。有些专家很早就提出建立共用系统来解决托盘回收再利用问题[3-4],但对于托盘共用系统中如何合理地进行回收、调度等研究还有待深入。任建华和章雪岩[5-7]针对托盘共用系统的回收问题,分别考虑到供给、需求、运输和装卸能力等因素的随机不确定性,提出了几个托盘共用随机规划模型,并采用机会约束规划方法对其进行求解。而对于托盘共用系统调度的全过程(购买或租借、分派、再分派、回收),任建华等[8]综合考虑损坏率、整车运输等众多极端不确定性因素,构建了一个混合型号托盘的托盘共用系统调度多情景规划模型,该模型能够帮助托盘共用系统管理者在没有充足历史数据情况下制定有效的托盘调度方案。吉清凯等[9]从管理层次、运输方式及研究方法等多角度对国内外关于集装箱的空箱调度研究进行了综述,并提到复杂空箱物流中的库存控制策略将是未来的发展方向之一。Li等[10]将多港口的空箱调度问题看作成具有正负需求的多阶段库存问题,提出了一种临界策略,并用启发式算法进行了求解。施欣[11]通过对海运集装箱空箱流转过程的分析,建立了空箱调运模型,并通过数字仿真分析了成本参数及载运能力对空箱调运策略的影响。计明军等[12]针对沿海港口间的空箱调运问题,提出了一种不确定目的港的空箱调运策略,建立了以总调运费用最小为目标的规划模型,采用遗传算法进行求解。卜祥智等[13]基于收益管理的思想,考虑海运集装箱需求的随机性,分别建立了考虑和不考虑空箱调运的集装箱舱位分配随机规划模型,并采用稳健优化的方法转化为确定性整数规划模型进行求解。
而对于物流网络中同级节点(比如库存节点、销售节点等)间的相互调货在研究中被称作库存共享或横向转运。这种策略可以降低整个系统的缺货成本和库存成本,同时提高系统的服务水平(降低缺货率),关于此类问题的综述性文献可见Paterson等[14]。针对不同仓储物品的特性,学者们的研究主要集中在备件的库存共享与消耗品的库存共享。最早关于备件的库存共享研究是Sherbrooke提出的METRIC模型[15],该模型针对航空领域可修复件,假设需求服从泊松分布,基于(S-1,S)的补货策略求得最佳的库存水平。Seidscher和Minner[16]针对备件的多点库存系统,基于one-for-one订货策略和需求服从泊松分布下,提出了一个半马尔科夫决策模型,并分别采用主动转运和被动转运策略进行分析。戢守峰等[17]针对三级备件分销网络,构建了考虑库存共享和服务水平限制下的横向转运模型,并针对模型具有非线性和复杂性的特点设计了贪婪算法进行了求解。Archibald[18]假设备件需求满足二项分布,构建了一个基于周期性检查补货策略的多点库存模型,分析了最优订货和调运策略的特点,并设计了三种简便的启发式调运策略。Wong等[19]考虑横向转运时间限制及延迟情形,构建了一个可完全共享的多点可修复库存模型,并转化成一个多维的马尔科夫模型进行求解。而最早关于消耗品的库存共享问题研究是Allen提出的[20],他考虑了一个在多个库存点之间的库存分配问题,各库存点的需求是独立随机的,在某一时点通过运输对各库存点的库存量进行重新分配,使得总的运输及未来缺货成本最小。Herer和Michal[21-22]针对消耗品,研究其在多个基地间的动态调运问题,在已知总订货量等于总需求量下,分别考虑固定订货成本、固定运输成本等限制条件,构建了多周期的动态调运模型,并借鉴Wagner和Whitin动态优化方法[23],设计了一个最优的求解算法对每个阶段的订货量和调运量进行求解。Özdemir等[24]研究了一个消耗品的多点库存系统,在已知各点的随机需求,考虑供应商生产能力限制,构建了一个随机型的多周期的调运模型,并采用样本均值逼近方法(SAA)进行了求解。以上研究都是基于多点间可以相互调运的情形,而对于单向的横向调运问题,Axsäter、Olsson等学者也进行了深入的研究[25-26]。还有些学者从不同的角度对多基地的库存共享问题进行了研究。陈敬贤和孟庆峰[27]针对两个销售商的库存系统,构建了一个应对突发事件的非合作博弈模型,证明了其纳什均衡解的唯一存在性,并设计了一个启发式的求解算法。
以上研究主要考虑在库存系统中遇到的各种不确定性因素,去解决回收再利用过程中的一次性调度问题;或针对备件或消耗品在不同特征下的多点库存系统,研究其补货或调运策略。而本文考虑的是航空公司机上周转品的多基地库存系统,研究其在一个订货周期内的动态补货问题,决策期初的订货方案以及周期内的调运方案,实现库存共享和降低成本。构建了一个库存优化模型,分析了最优解的性质,并设计了相应的算法进行求解,通过算例验证了方法的有效性。
2 问题与模型构建
2.1 问题描述
某航空公司拥有多个基地,每个基地设有一个存储仓库和一个回收仓库,负责机上周转品的采购、仓储、配备及清洗。各基地的存储仓库设有一定的安全库存来应对未来一段时间内的需求,并且机上周转品在回收仓库经过一段时间(清洗周期)后可以返回存储仓库再次使用。各基地之间每天都有往返航班,当某个基地的库存量低于安全库存量时,可通过航班由其它基地进行调运。在期初,航空公司根据整个库存系统的需求统一订货,然后再根据各个基地的需求进行分配。已知每个基地的需求量、回收量和安全库存量,求各个基地在期初的订货量以及每天的调运量,使得整个系统在一个订货周期内所产生的总成本(订货成本、存储成本、调运成本及回收处理成本)最小。
2.2 基本假设与参数说明
基本假设:
1)不考虑订货提前期,即供货方的生产能力足够大;
2)各基地的运输能力足够大,并且可以在当天完成。
3)各基地的仓库容量足够大。
4)机上周转品在每个基地的回收周期和损耗比例为常数。
参数设置:
基本参数
N:基地集合
T:订货周期
Si0:基地i的初始库存量,i∈N
sit:基地i第t天的安全库存量,i∈N,t∈T
dit:基地i第t天的需求量,i∈N,t∈T
rit:基地i第t天的回收量,i∈N,t∈T
决策变量
xi:基地i期初的订货量,i∈N
yijt:第t天基地i调运到基地j的机上周转品数量,i≠j,i,j∈N,t∈T
过程变量
Iit:基地i第t天的库存量
整个系统在订货周期内产生的总成本包括总订货成本、总存储成本、总调运成本以及总回收处理成本,即:
(1)
其中,ci为基地i的单位订货成本,hi为基地i存储仓库的单位存储成本,pij为从基地i到基地j的单位调运成本,qi为基地i回收仓库的单位回收处理成本。
由于各基地的回收量已知,那么整个系统总回收处理成本为确定值,故不将此项成本计入目标函数中。
2.3机上周转品多基地库存优化模型(R1)
(1.1)
s.t.Ii0=Si0+xi
(1.2)
(1.3)
Iit≥sit
(1.4)
xi,Iit,yijt∈Ν
(1.5)
约束(1.2)表示第0天基地i的库存量等于其初始库存量与订货量之和;约束(1.3)表示基地i第t天的库存平衡关系式;约束(1.4)表示基地i第t天的库存量必须大于或等于其安全库存量;约束(1.5)表示变量约束,都为非负整数。
3 模型求解与算法
令Iit=sit+zit且si0=Si0,那么模型R1中的目标函数(1.1)可以表示成:
(2)
由于各基地的安全库存量已知,因此等式(2)右边第三项为确定值,亦可以不计入模型目标函数中。那么,模型R1等价于如下模型(R2):
(2.1)
s.t.xi=zi0
(2.2)
(2.3)
xi,zit,yijt∈Ν
(2.4)
该模型是一个线性整数规划模型,并且变量较多,直接求解非常困难。本文将在模型最优解分析的基础上,给出一个多项式求解算法,求得问题的最优解。
3.1 最优解分析
令
X1=
X2=
证明:见附录,下同。

(C1)c1=c2=…=cN=c;
(C2)h1=h2=…=hN=h;

因此,当模型R2的参数满足条件(C1)-(C3)时,模型R2的最优解等价于求解如下模型(R3)的最优解:
(3.1)
s.t.xi=zi0
(3.2)
(3.3)
(3.4)
xi,zit,yijt∈Ν
(3.5)
为此,将模型R3转化为最小费用最大流问题进行求解。剩下的问题就是如何去构造网络,以及如何得到最小费用最大流。
3.2 网络流求解算法及最优性
针对模型R3,构造一个多基地动态补货网络,记为D(0)=(V,A,C,B),对于每一条弧(vi,vj)∈A上,都对应有一个容量和单位费用对(cij,bij),如图1所示。

图1 多基地动态补货网络
其中,节点s为发点,节点t为收点,节点0为订货点,节点1、2为虚拟点,节点(i,j)为基地i的所有库存点(i=1,2,…,N,j=1,2,…,T),M为一个很大的数;并称节点0到节点(i,1)的弧为订货弧(i=1,2,…,N),节点(i,j)到节点(i,j+1)的弧为库存弧(i=1,2,…,N,j=1,2,…,T-1),节点(i,j)到节点(k,j)的弧为调运弧(i≠k,i,k=1,2,…,N,j=1,2,…,T),节点1到节点(i,j)的弧为回收弧(i=1,2,…,N,j=1,2,…,T),节点(i,j)到节点2的弧为需求弧(i=1,2,…,N,j=1,2,…,T)。
令节点s到节点0的弧、回收弧和需求弧的集合为τ,那么多基地动态补货网络流模型,如下所示:
(4.1)
s.t.fij=cij(vi,vj)∈τ
(4.2)
0≤fij≤cij(vi,vj)∈A-τ
(4.3)
fij∈Ν(vi,vj)∈A
(4.4)
考虑到网络D(0)=(V,A,C,B)中存在双向的调运弧,借鉴文献[28]的方法,即若存在两个不同的顶点i和j,使得弧aij=(i,j)和aji=(j,i)都存在,那么在弧aij=(i,j)中增加一个虚拟点x,把弧aij=(i,j)变成两条弧aix=(i,x)和弧axj=(x,j),使得c(aix)=c(axj)=cij,b(aix)=b(axj)=0.5bij,直到任意两个不同顶点间最多存在一条弧为止,并将此时的网络记为D(1)。那么,将含有回收的动态网络流模型的求解算法可以分为三步:
步骤1:取f(0)=0,为初始流。令k=0,在网络D(1)中构造赋权有向图W(f(k));
步骤2:在W(f(k))中,寻求从发点vs到收点vt的最短路,若不存在最短路(即最短路权是+),则f(k)就是最小费用流,算法结束;若存在最短路,则在原网络中得到相应的增广链μ,在增广链μ上对f(k)进行调整。调整量为:令
得到新的流f(k+1),转步骤3;
步骤3:对f(k+1)重复步骤2。
定理2在含有回收的动态补货网络流模型中采用最小费用流求解算法得到的流f*,其订货弧、调运弧、库存弧上的流量即为模型R3的最优解。
由于求解期初最优订货总量的算法时间复杂度为Ο(N*T),而在网络中寻找从发点到收点的最短路的算法平均时间复杂度约为O(|V|2)=O((N*T+5)2),增广次数最坏情况下为X1,因此,整个算法的时间复杂度约为O(X1*(N*T)2)。
3.3 启发式求解算法

这说明原问题最优的总订货量也一定落在区间M上,其中,M=[X1,X2]。
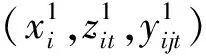

为此,我们结合上述的网络流求解算法,针对原问题即模型R2设计一个启发式算法,具体算法步骤如下:
步骤1:调整网络D(0)的容量和单位费用对,将节点0到节点(i,1)的弧(即订货弧)上的费用调整为ci,节点(i,j)到节点(i,j+1)的弧(即库存弧)上的费用调整为hi,调整后的网络记为D(2)。
步骤2:将区间M=[X1,X2]等分成Q份,其中各端点分别记为Xi=X1+⎣i(X2-X1)/Q」,其中⎣*」表示向下取整。

4 算例
本文以国内某大型航空公司为例,分析某一种机上周转品(沙拉碗)在一个订货周期内的补货策略。该公司在全国拥有八个基地,各基地位置及调运网络如图所示。
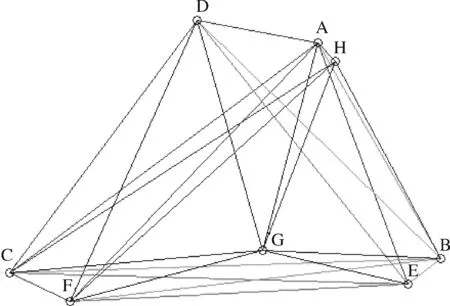
图2 各基地位置及调运网络图
假设订货周期T=7(天),各基地的参数设置如下:机上周转品的单位订货成本为10(元/个),单位存储成本为0.1(元/个*天),单位调运成本为0.01(元/个*天),初始库存量、日需求量、日回收量及日安全库存量见表1~4。
由于上述参数满足定理1的条件,因此通过定理1的计算公式可以得到期初最优的订货总量为:x*=3571。

表1 各基地的初始库存量

表2 各基地的日需求量

表3 各基地的日回收量
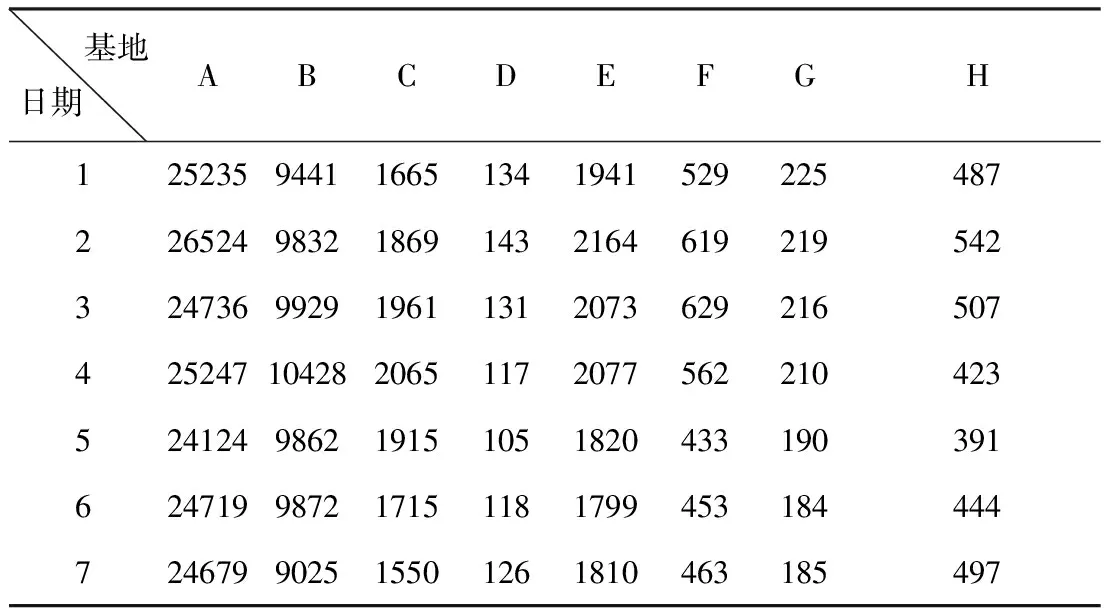
表4 各基地的日安全库存量
通过最小费用流求解算法进行求解,最终得到各基地最优的期初订货量和每日最优的调运量,见表5~6:

表5 各基地期初最优的订货方案
下面分析各基地单位调运成本不同的情形,假设基地A与基地C之间的单位调运成本为0.02(元/个*天),而其它参数保持不变。从定理1可知,期初最优的订货总量依然为3571(个)。而各基地的期初最优订货方案以及每日的调运方案如下:

表6 各基地间最优的调运方案

表7 各基地期初最优的订货方案

表8 各基地间最优的调运方案
由于基地C到基地A的单位调运成本的增加,使得基地C调出到基地A的量减少,调出到其它基地(B、E、F、H)的量增加,进而使得基地A的期初订货量增加,其它基地(B、E、F、H)的期初订货量减少。由此可以看出,订货和调运方案会受到各基地之间的单位调运成本的影响。
接下来分析当各基地的单位订货成本和单位存储成本不相同的情形。通过引理2的分析,得到各基地的期初缺货量(见表9)。

表9 各基地的期初缺货量
因此,原问题的期初最优订货总量所处的区间为[3571,4151]。
假设基地A的单位订货成本为5(元/个),而其它参数不变。令Q=10,ε=10-3,通过启发式算法得到一个较优的订货和调运方案如下:

表10 各基地期初的订货方案

表11 各基地间的调运方案
假设基地A的单位存储成本为0.5(元/个*天),而其它参数不变。令Q=10,ε=10-3,同样通过启发式算法得到一个较优的订货和调运方案如下:

表12 各基地期初的订货方案

表13 各基地间的调运方案
通过上述两个例子,可以得出期初的订货方案和每天的调运方案同样也会受到单位订货成本以及单位存储成本的影响。
通过该启发式算法只能得到众多可行解中的一个较优的订货和调运方案,而通过对3.1节最优解的分析,当不满足条件(C1)-(C3)下,目标函数的单调性无法确定,进而模型的最优解很难得到,故而该启发式算法的精度也不能确定;当满足条件(C1)-(C3)下,因为启发式算法的可行解中包含最优订货量(X1),故最终得到的解相同。
接下来分析不同单位成本参数对整个系统总库存成本的影响情况(见图3~5)。

图3 基地A的单位库存成本的变化对整个系统总库存成本的影响

图4 基地之间的单位调运成本的变化对系统总库存成本的影响

图5 基地A的单位订货成本的变化对系统总库存成本的影响
由此可见,各基地的单位订货成本、单位存储成本以及各基地之间的调运成本会影响整个系统的总库存成本,进而影响到整个系统的订货和调运方案。
5 结语
本文研究航空公司机上周转品多基地库存优化问题,构建了一个单周期的动态补货模型。该模型在已知每个基地的每日需求量、回收量及安全库存量下,对期初的订货量以及每日的调入调出量进行决策,使得整个系统的库存总成本(包括订货成本、存储成本、调运成本、回收成本)最小化。并对该模型的最优解进行了分析,参考网络流算法,给出了一个在成本参数满足一定条件下的多项式求解算法;此外,设计了一个求解原问题的启发式算法。最终结合实际的例子,验证了算法的有效性。但本文所提出的问题还有待深入研究的地方,比如考虑随机需求、扩展到多周期的补货问题等。
附录:
(1)引理1的证明



(2)引理2的证明

(3)引理3的证明
当条件(C1)(C2)成立时,将约束条件(2.2)-(2.4)代入模型R2的目标函数G(xi,zit,yijt)并化简可得:
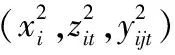

(4)定理1的证明
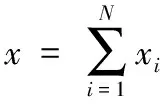
(5)定理2的证明
对于最小费用流模型中的任何一个可行流f,若令节点0到节点(i,1)的弧上的流量为xi(i=1,2,…,N),节点(i,j)到节点(i,j+1)的弧上的流量为zij(i=1,2,…,N,j=1,2,…,T-1),节点(i,j)到节点(k,j)的弧上的流量为yikj(i≠k,i,k=1,2,…,N,j=1,2,…,T),而其他弧上的单位费用为零,故由(4.1)可知此流的总输送费用为:
由于f是一个可行流,因此由约束条件(4.2)可知其节点s到节点0的弧、回收弧和需求弧上的流量都等于其容量,并令xi=zi0,那么对任一个节点(i,j),由出入流量平衡可知,
并且由约束(4.4)可知,xi,zit,yijt∈Ν,因此含有回收的网络流模型中所有的可行流上订货、库存和调运弧的流量皆为模型R3的可行解,并且目标函数都一致。
下证,最小费用流算法一定能得到含有回收的网络流模型中使得总费用最小的可行流。在含有回收的动态补货网络D(0)中,当发点vs到订货点v0弧上的流量fs0小于其容量x*时,对于任意一个基地i,一定存在一条从发点vs到收点vt的路ξ,这条路经过订货点v0和基地i的所有库存点vit,且权值为c+Th<+。因此按照最小费用流算法可以依次调整权小于等于c+Th的从发点vs到收点vt的路(增广链)上的流量,此时增广链上一定包含弧集合τ中的一条或多条弧,直到弧集合τ上所有弧的流量都等于其容量,此时,已找不到从发点vs到收点vt的最短路,那么最终得到的流f*是最小费用流模型的一个可行流;由最小费用最大流问题可知,f*是所有流量等于的总费用最小的一个流,故f*是最小费用流模型中使得总费用最小的可行流。
