我国的通货膨胀与名义利率粘性：长期与短期费雪效应

杨利雄，李庆男

(1.兰州大学管理学院， 甘肃 兰州 730000；2.台湾中山大学经济研究所，台湾 高雄 80611)

1 引言

利率作为资金市场借贷的价格，是一个重要的经济杠杆，利率不仅影响微观个体的消费、储蓄和投资决策，而且影响宏观经济政策的制定，利率干预是传统凯恩斯主义熨平经济周期并促进经济增长的最主要的货币政策主张之一[1]。Fisher[2]提出费雪效应阐述了名义利率和通货膨胀之间的关系，即在一个信息充分且具有完美预见(Perfect foresight)的市场，名义利率和通货膨胀预期之间的变动存在一一对应关系。因此，费雪效应成立时实际利率与通胀无关，这使得政府不能通过货币政策来影响实际利率进而干预实体经济，即货币是中性的，故而，费雪效应成立时货币政策是无效的。

在新凯恩斯主义经济理论框架下，货币政策的有效性依赖于货币非中性，而货币非中性的主要来源是名义价格粘性[3]。因此，随着我国的货币政策框架逐渐从数量型向价格型转变[4]，检验费雪效应在我国是否成立以及名义利率的动态调整是否存在粘性，不仅有助于理解通胀与利率之间的传导关系，对货币政策的操作也具有重要的现实意义。

随着协整理论的提出，通过检验名义利率与通货膨胀之间的协整关系，进而检验费雪效应成为近几十年中的一个研究热点。学者对该问题进行了大量的研究，有些研究支持费雪效应，同时也有些文献不支持费雪效应[5-6]。Rose[7]使用Engle-Granger两步法研究了美国的年度数据，发现即使在10%的显著性水平下，依然没有费雪效应成立的证据；Wallace和Warner[8]基于美国的季度数据和Johansen检验，发现费雪效应成立。其后，Million[9]使用门限自回归模型也发现美国存在费雪效应。近年来，部分学者对我国的费雪效应的存在性也进行了有益的探索。然后，研究结论也不一致。刘金全等[10]运用分数协整方法研究表明我国不存在费雪效应；刘康兵等[11]使用Engle-Granger两步法研究的结果表明我国存在费雪效应。同时随着非线性模型的提出和发展，近期文献使用非线性协整模型检验了我国费雪效应的存在性。如王少平和陈文静[12]使用非参数单位根检验和非参数协整检验的研究支持费雪效应；封福育[13]、陈海燕和李松臣[14]等使用门限模型研究了我国的月度数据，其结果也支持费雪效应。

然而，现有的国际文献和国内文献中，考察费雪效应时通常假设实际利率是稳定不变的常数，而实际利率取决于生产率、人们的时间偏好等因素[8]，因此实际利率不变的假设很难成立。进一步地，根据Perron[15]，在ADF单位根检验中，常数项的结构突变或时变性会造成单位根检验的低功效问题，因而忽略实际利率的时变性，可能造成严重的协整检验功效损失，使得我们无法发现存在的费雪效应；同时，根据Yang Lixiong等[16]的研究，忽略单位根检验中常数项的结构突变还可能造成虚假拒绝问题，因而忽略实际利率的时变性，还可能造成严重的协整检验水平扭曲，使得我们错误地拒绝不存在协整关系的原假设。因此，基于实际利率不变的假设研究费雪效应是不合适的。其次，使用门限模型研究名义利率与通货膨胀的关系时，封福育[13]、陈海燕和李松臣[14]等使用通货膨胀作为门限变量，门限模型要求门限变量是平稳的，否则参数估计的一致性无法保证，而通货膨胀常常是非平稳的。再次，现有研究在考察费雪效应时，主要着重于考察名义利率和通货膨胀的长期均衡关系，并未考虑名义利率的短期调整特征以及调整的不对称性，然而，名义利率的短期调整特征可能有助于识别名义利率是否存在粘性，从而判断货币政策的有效性以及合理性，因而具有重要意义。

文献中研究费雪效应的常用方法是协整模型，但传统的协整模型参数为常数。经济理论提供了充足的理由支持实际利率的时变性，但实践中刻画真实利率的时变性依然是一个重大挑战[17]，因此建立适当的模型刻画和检验实际利率的时变性具有重要意义。在协整框架下，Gregory和Hansen[18]假设常数项存在跳跃，并且通过加入虚拟变量捕捉该跳跃扩展了Engle-Granger协整检验。该方法具有重要的应用价值，但如果存在多次跳跃，则需要加入多个虚拟变量，且实际利率的时变结构是未知的，而跳跃点的位置和跳跃点的个数常常难以准确估计。傅里叶变换能以任意的精度近似经济变量中的常见时变特征[19]。单一频率的傅里叶近似就能很好地近似常见的时变特征(包括跳跃型的结构突变)，而几个频率的累加通常能得到更精确的近似(参见图1)。因此，本文首先使用傅里叶变换捕捉实际利率的时变性特征， 扩展Gregory和Hansen[18]的常数项存在跳跃的协整模型，并给出模型的设定检验方法，用以研究我国的费雪效应。其次，建立门限模型考察名义利率向均衡的动态调整特征以及名义利率是否具有粘性，这对理解费雪效应和制定货币政策具有重要意义。由于存在菜单成本，名义利率可能具有粘性，同时，信息不对称、银行市场竞争的不完全等因素的影响都有可能影响利率的动态调整特征。在一篇经典的文献中，Stiglitz和Weiss[20]指出：由于道德风险和逆向选择，银行会倾向于设定低于市场均衡的贷款利率，即著名的“信贷配给(Credit rationing)”假说。而De Bondt等[21]则认为即使存在道德风险和逆向选择，如果银行市场竞争充分，“信贷配给”也可能不会发生。因此，为考察我国名义利率是否存在粘性及其向均衡的短期动态调整特征，本文将建立门限误差修正模型用以描述短期的费雪效应特征。

本文选取1991年1月至2017年12月的月度数据为研究对象。参照王少平和陈文静[12]、封福育[13]等文献，名义利率选取一年期贷款利率，通货膨胀率选用全国消费者价格指数的变化率。研究发现：在样本期，使用传统的Engle-Granger两步法，即使在10%的显著性水平下依然不支持费雪效应；为排除可能的检验功效损失和虚假拒绝问题，建立统计量检验实际利率的时变性，发现强烈的证据拒绝实际利率为常数的假设；在考虑实际利率时变性特征的基础上，在1%的显著性水平下支持名义利率和通货膨胀之间存在协整关系，即我国存在费雪效应；进一步地，建立门限误差修正模型考察短期的费雪效应特征，研究发现了双重门限效应，当名义利率低于均衡值和处于中间机制时，名义利率存在“粘性”，而当名义利率对均衡值出现较高的偏离时，则会出现显著而快速的调整，本文尝试从菜单成本、市场竞争格局和信贷配给等视角为上述现象提供了可能的解释，并探讨了相关的货币政策含义。

与已有文献相比，本文的贡献主要体现在两个方面：第一，在研究方法方面，使用傅里叶变换处理时变参数，扩展了Gregory和Hansen[18]的方法，并给出了检验参数时变性和选择傅里叶函数的累加频率的方法，丰富了协整框架下的实证研究方法；第二，在实证问题方面，使用傅里叶变换近似实际利率，并检验了实际利率的时变性，同时提供了我国存在“弱费雪效应”和名义利率“粘性”的证据，为当下数量型货币政策和价格型货币政策的使用提供了研究支撑。

2 模型与方法

费雪效应揭示了名义利率和预期通货膨胀之间的关系。根据费雪效应，当预期通货膨胀率上升时，名义利率也会上升。费雪效应可表示为：

(1)

it=β0+β1πt+zt

(2)

因此，对费雪效应的检验就转化为对模型(2)的估计和检验。若H0:β1=1成立，表明存在完全的费雪效应，即货币是中性的，从而货币政策是无效的；若H0:0<β1<1成立，表明存在弱费雪效应，则货币非中性，因而货币政策是有效的。

然而，现有研究通常假设实际利率是常数，如王少平和陈文静[12]、封育福[13]、陈海燕和李松臣[14]等，给定实际利率依赖于经济周期、生产率、时间偏好等[4]，并没有充足的理由认为真实利率是恒定不变的。当模型(2)中β0存在时变性特征或结构突变时，Engle-Granger协整检验第二步所依赖的ADF单位根检验存在低检验功效问题[15]或虚假拒绝问题[16]，从而使得协整关系无法被识别出来或在不存在协整的情况下错误地得到存在长期均衡的结论。Gregory和Hansen[18]提出的协整框架下，模型参数可以允许时变特征：

it=α1+(α2-α1)DUt+βπt+zt

(3)

图1 常见时变特征的傅里叶近似注： (a)为跳跃型结构突变(abrupt break);(b)由平滑转移函数(smooth transition function)生成； (c)和(d)为平滑转移函数生成的含多个突变点的序列。

因此，考虑使用傅里叶变换近似实际利率的时变特征：

it=α(t)+βπt+zt

(4)

(5)

其中，k为频率参数。在实证应用中，Yang等[16]建议考虑选择k≤5的单一频率，而Becker等[19]在对通胀和货币需求建模时， 指出：多个频率的累加可以更好地近似时变特征。如图1所示，少数几个频率的累加就能非常精确地近似常见时变特征。因此，为了确定实际利率是否存在时变性特征、是否应该使用多个频率，以及频率累加个数n，本文将建立如下设定检验，记α(t)为恒定常数时模型(4)的残差平方和为SSR0，α(t)含单一频率傅里叶函数时模型(4)的残差平方和为SSR1(k)，α(t)含两个频率累加的傅里叶函数时模型(4)的残差平方和为SSR2，以此类推，SSR3为α(t)含三个频率累加的傅里叶函数时模型(4)的残差平方和。然后考虑如下检验统计量：

(6)

如果统计量supF0超过临界值，则拒绝α(t)为常数时的模型，而考虑α(t)具有时变特征的模型。进一步地，为了选择傅里叶函数的累加频率n，考虑：

(7)

如果统计量F1超过临界值，则拒绝α(t)含单一频率傅里叶函数时的模型，进而考虑两个及两个以上的频率累加。使用类似于(7)的检验统计量，选择最优的频率累加n*。上述检验的实现使用Bootstrap方法，相关计算均使用GAUSS 10.0软件编程实现。

同时，在线性模型框架下，学者们无法解释不同通胀水平下名义利率与通胀之间所呈现的不同关系[13]，因而很多文献认为通胀与名义利率关系的分析需要考虑机制转移特征[13-14]。另一方面，长期利率取决于真实经济因素，Fisher[2]指出：费雪效应在长期成立。而短期利率则很可能受到短期货币政策因素的影响，出现对均衡的偏离。因此，考虑建立门限误差修正模型，区别长期的费雪效应和短期的费雪效应特征：

(8)

其中，zt为均衡误差，滞后阶数m,n使用AIC信息准则确定。

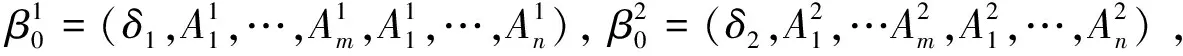
(9)

3 实证分析

3.1 数据来源和指标选择

本文名义利率选取一年期贷款利率的月度数据，通货膨胀选择月消费者价格指数(CPI)的变化率，样本区间选取1991年1月至2017年12月，数据来源于国泰安数据库。

3.2 单位根检验和协整检验

在样本区间内，表1是对名义利率和通货膨胀率序列进行单位根检验的结果。单位根检验表明：对名义利率和通货膨胀率，存在单位根的原假设不能被拒绝，而在对名义利率和通货膨胀率的差分进行单位根检验时，在1%的显著性水平下原假设被拒绝。因此，名义利率和通货膨胀率是一阶差分平稳的。

表1 单位根检验

注：***表示在1%的显著性水平下显著。

基于标准的Engle-Granger两步法，检验名义利率和通货膨胀率之间是否存在长期均衡关系。研究发现：即使在10%的显著性水平下，依然无法拒绝不存在协整关系的原假设。因此，基于模型(4)和(5)，在考虑实际利率时变特征的基础上检验协整关系。首先，基于(6)式的统计量考察是否存在时变特征，计算得到：supF0=2044.44(p值=0.000)，然后使用(7)式选择最优累加频率数，得到最优频率n*=4。在此基础上，估计模型(4)和(5)，发现除sin(2π3t/T)外，其他傅里叶项都在1%的显著性水平下显著(见表2)，然后检验残差序列的平稳性，发现1%的显著性水平下拒绝不存在协整的原假设，因此，名义利率和通货膨胀率之间存在长期均衡关系，但实际利率是时变的(图2)，而实际利率的时变特征影响了标准Engle-Granger协整检验的检验功效，使得标准的E-G两步法无法捕捉到长期费雪效应。然而，在协整关系中引入实际利率时变性特征后的模型(4)和(5)，则表明存在长期的弱费雪效应。与发达国家相比，如美国的费雪效应值在0.821-1.095之间，加拿大的费雪效应值在0.796～0.895之间[12]，我国费雪系数明显较小，这表明货币非中性假设在我国更加适合，进而我国可能有更大的货币政策操作空间。

从图2发现：真实利率的变化并不总是引起名义利率的变化，即名义利率可能存在粘性。名义价格粘性是货币政策有效的重要基础。因此，下文分析名义利率的短期调整特征，考察我国名义利率是否存在粘性，以及名义利率的短期动态调整特征。

3.3 短期的费雪效应与名义利率粘性

首先，使用Bootstrap检验门限效应的存在性。重复抽样1000次，不存在门限效应的原假设被拒绝，p值为0.008，存在一重门限效应的原假设也被拒绝，p值为0.000，而存在双重门限效应的原假设在10%的显著性水平下不能被拒绝，因此模型(8)中存在双重门限效应。

其次，在双重门限效应存在的基础上，使用AIC信息准择选择滞后阶数并估计双重门限效应误差修正模型(8)，得到如下式所示的模型估计(括号中为参数估计的标准误)：

Δit=

表2 模型(4)和(5)的估计

注：sink表示sin(2πkt/T)，cosk表示cos(2πkt/T)，k=1,2,3,4。

图2 1991年1月至2017年12月的名义利率和估计的实际利率

图3 门限值的估计与置信区间

门限误差修正模型的估计结果表明：当名义利率对均衡值出现较高的偏离(即均衡误差大于0.788)时，出现了明显的误差修正，因为此时误差项系数为-0.23且在1%的显著性水平下显著；然而，当名义利率低于均衡值(即均衡误差小于-0.262)或处于中间机制(即均衡误差位于-0.262与0.788之间)时，没有发现明显的误差修正现象，因为这两种情况下的误差项估计为正数且在10%的显著性水平下不显著。即，当名义利率高于均衡值时，为了避免因高利率而引起的逆向选择，银行倾向于迅速调低一年期贷款利率，表现为当名义利率的均衡误差大于0.788时，出现了显著的误差修正；而当名义利率低于均衡值时，并未发现显著的误差修正现象，即银行倾向于定一个低于市场均衡的利率。使用利率市场化路径划分子样本，上述实证结论依然成立。

上述实证发现表明：我国的一年期贷款利率存在“粘性”，即当名义利率低于均衡值时，并没有迅速的调整到均衡利率水平。一个可能的原因是我国利率的市场化程度还较低，存在市场管制[13,23]。本文跳出市场管制的观点，从约束条件下理性人最大化利润的角度去解释市场粘性，我国名义利率的粘性可能由以下原因引起：首先，名义利率的调整存在“菜单成本”，使得只有当均衡偏离足够大时，银行才会调整贷款利率；其次，由于银行市场的竞争，银行为维护客户避免过度利率波动的影响，可能会做出平滑贷款利率的举措；此外，在银行寡头市场，银行推测其他银行对自己利率变动的态度是“跟跌不跟涨”，因而可能引起信贷的需求曲线是“弯折的”，因而只有当银行的成本变动足够大时，才会调整利率。另一方面，我国银行市场呈现寡头市场特征，而银行之间的竞争程度和市场的不完全使得银行具有市场势力(Market power)，进而银行可能维持一个较高的利率[17]，本文的证据不支持上述假说；与之相反，Stiglitz和Weiss[20]指出：因为信息不对称引起的道德风险和逆向选择的影响，银行倾向于定一个低于市场均衡的利率，即著名的“信贷配给”(Credit rationing)，从而激励贷款人揭露关于还款风险的信息。因此，市场的信息不对称使得借贷利率的调整滞后于货币政策[24]。本文的实证结果与“信贷配给”观点一致。

综上，在长期我国仅存在“弱费雪效应”；在短期名义利率存在“粘性”，即当名义利率低于均衡值和处于中间机制时不会迅速调整到均衡利率水平，而当名义利率对均衡值出现较高的向上偏离时，则会出现显著而快速的调整。因而，当通胀上升，使得名义利率出现向下偏离时，名义利率不会出现显著的向上调整使其回到均衡；而当通胀回落使得名义利率出现向上的偏离时，名义利率能快速回到均衡水平。

传统经济理论认为通过数量型货币政策可以刺激经济或抑制通胀[25]，但数量型货币政策只能调控货币总量，而无法解决经济和金融结构失衡的问题，因此2012年以后我国更重视价格型货币政策工具[4]，以期实现降杠杆、防风险的目的。上世纪90年代以来，随着科技进步、金融脱媒和影子银行的持续发展，尤其是表外理财业务的出现，大量资金由表内转向表外，导致货币数量的相关指标逐渐失效，给数量型货币政策带来困难。因而欧美国家放弃了数量型货币政策，转而采用价格型货币政策。近年来，随着我国金融创新带来的影子银行、互联网金融、资管通道类业务的爆发式增长，数量型中间目标的可测性、可控性大幅下降，经济和金融的结构失衡问题开始显现，因此货币政策的目标在稳增长、防通胀的基础上，新增去杠杆、防风险。那么，在此背景下我国货币政策与欧美国家有何异同呢？

不同于欧美国家(如美国的费雪效应值在0.821～1.095之间[12])，我国长期存在的“弱费雪效应”表明利率对通胀反映不足，因而依靠利率控制通货膨胀的效果较差，但货币非中性依然成立，货币政策引起的通货膨胀变化只能部分传导到企业借贷利率，货币供给增加引起的物价上升仅会引起利率微弱的上升；且我国存在短期“名义利率粘性”，当利率低于均衡值时不会出现快速修正，这进一步支持了短期货币非中性，因而通过数量型货币政策刺激经济增长在我国是仍然可行的，即数量型货币政策在我国依然有用。上述研究结果意味着：与欧美国家不同，我国现阶段仍存在实施数量型货币政策的空间，即我国货币政策可以根据不同阶段政策目标的差异在数量型货币政策和价格型货币政策之间相机抉择，因而存在综合使用数量型货币政策和价格型货币政策的空间。

4 结语

考察费雪效应在我国是否成立以及名义利率的动态调整是否存在粘性，不仅有助于理解通胀与利率之间的传导关系，对货币政策的操作也具有重要的现实意义。为了研究名义利率与通货膨胀的关系，本文将费雪效应区分为长期费雪效应和短期费雪效应，使用傅里叶变换近似实际利率考察长期费雪效应，并建立门限误差修正模型刻画名义利率短期的动态调整特征。研究发现：(1)我国名义利率和通货膨胀之间存在长期的弱费雪效应；(2)名义利率的短期动态调整特征存在双重门限效应，在名义利率过度高于均衡值时会出现显著而快速的调整，而当名义利率低于均衡值或处于中间机制时，没有发现显著的调整，即名义利率存在粘性。名义利率短期的调整特征与“信贷配给”假说和“菜单成本”假说一致。我国的弱费雪效应和名义利率粘性表明：与欧美国家不同，我国现阶段的货币政策可以根据不同阶段政策目标的侧重点在数量型货币政策和价格型货币政策之间相机抉择，因而存在综合使用数量型货币政策和价格型货币政策的空间。