物流选址方法在舰载机飞行甲板调运中的应用

李晓杰,谢 君,傅 冰

(海军工程大学电子工程学院,湖北 武汉 430033)



物流选址方法在舰载机飞行甲板调运中的应用

李晓杰,谢 君,傅 冰

(海军工程大学电子工程学院,湖北 武汉 430033)

为提高飞行甲板舰载机调运作业效率,引入物流选址方法解决舰载机调运路径规划问题。针对飞行甲板调运环境复杂和舰载机形状不可忽略的难点,以美“尼米兹”级航母为研究对象,首先对飞行甲板和舰载机实体进行了几何建模,然后借鉴物流选址方法,通过某种评价机制在飞行甲板上设置若干个候选调运节点,并采用免疫算法进行优化选择进而确定调运网络,最后通过状态变迁图进行多机调运时序控制。对六机出动作业调运过程进行仿真,结果表明该方法规划出的调运路径简单合理,可为舰载机调运管理人员提供决策参考。

舰载机调运;物流选址;免疫算法;时序控制;状态变迁图

航空母舰(简称“航母”)是大国军事力量的集中体现,其作战任务的完成主要依靠上面搭载的各型舰载飞机,正是依靠这些舰载机,航母能够在远离国土的地方对敌施加军事压力和进行作战。现代战争节奏加快,舰载机的出动回收效率很大程度上决定了能否有效夺取局部制空制海权,进而决定了战争的胜败[1]。在较短的时间内为舰载机规划出一条合理的调运路径,能够有效缩短舰载机的出动准备时间,从而最大限度的发挥舰载机的作战能力。

按调运环境划分,舰载机在航母上的调运作业可分为机库调运作业和飞行甲板调运作业;按舰载机出动规模划分,舰载机出动作业可分为单机出动作业和多机出动作业。飞行甲板环境相较于机库环境更加复杂,其搭载的舰载机调运作业更加频繁且时间要求更高,因而对飞行甲板舰载机调运作业进行路径规划意义明显。舰载机调运路径规划不同于简单的机器人路径规划,舰载机形状相对于有限的飞行甲板调运空间不能够简化为质点处理,因此需要采用适合于舰载机的路径规划方法。目前大部分相关研究[2-6]集中在对调运环境进行精确建模,采用严格的数学计算求解最优路径,然而由于飞行甲板环境复杂且舰载机形状不规则,这种方法计算复杂且实用性不高。杨炳恒等[7]通过分析俄“库兹涅佐夫”号航母舰载机出库流程,建立了舰载机调运作业交通网,将牵引轨道、转盘等设施作为调运作业的关键节点,从而将舰载机调运问题转化为调运网络时序优化,该方法可为飞行甲板舰载机调运问题提供借鉴。刘亚杰等[8]基于Petri网建立了舰载机出库逻辑关系模型,借此求出舰载机的可达性和冲突等待问题,可作为调度方案优化过程中时序控制的依据。

飞行甲板舰载机调运作业需要在满足安全的前提下,尽量缩短调运作业时间。多机调运作业时,多架舰载机的“联动”非常重要,若不能提前规划出路径,并合理安排调运顺序,将很容易导致调运阻塞。为避免调运作业混乱,引起舰载机碰撞等不可挽回的损失,本文引入物流选址方法,通过对飞行甲板环境进行建模,在甲板上设置若干个调运候选节点,并通过免疫算法进行节点选择,从而确定舰载机调运网络,并通过状态变迁图进行时序控制来解决舰载机在飞行甲板环境中的调运路径规划问题。此方法的优点在于:可以充分利用规划得到的调运网络,实现任意两站位之间的舰载机调运作业;可以合理安排多机调运时序,减少时间浪费,从而提高调运作业效率。

1 调运环境建模

1.1 调运流程分析

舰载机调运作业包括舰载机在任意两个停机站位之间的调运以及舰载机移动到起飞准备站位的调运,二者可作为同一模型处理。美“尼米兹”级航母可搭载固定翼飞机约80架,飞行甲板可停放大约一半的舰载机,并可通过四部升降机转运至机库。全舰配置四部弹射器,弹射器前部设有起飞准备站位,用于停放即将弹射起飞的舰载机。航母舰载机每次出动任务一般包含数架舰载机。典型的飞行甲板舰载机出动作业流程为:接到起飞命令,在站位完成加油、供电、充气、补充雷弹等一系列保障作业,然后开始沿规划路径牵引滑行,直至牵引至弹射器前的起飞准备站位就位,待弹射装置冷却后就进行舰载机的弹射起飞作业。舰载机完成作战任务后返航着舰,舰面工作人员和舰面设备移动舰载机在飞行甲板就位或转移至飞行甲板下面的机库甲板。着舰跑道作为一个特殊区域,可用于暂时停放舰载机,一旦有舰载机返航着舰,则着舰区域必须空闲。飞行甲板舰载机作业流程逻辑模型如图1所示。

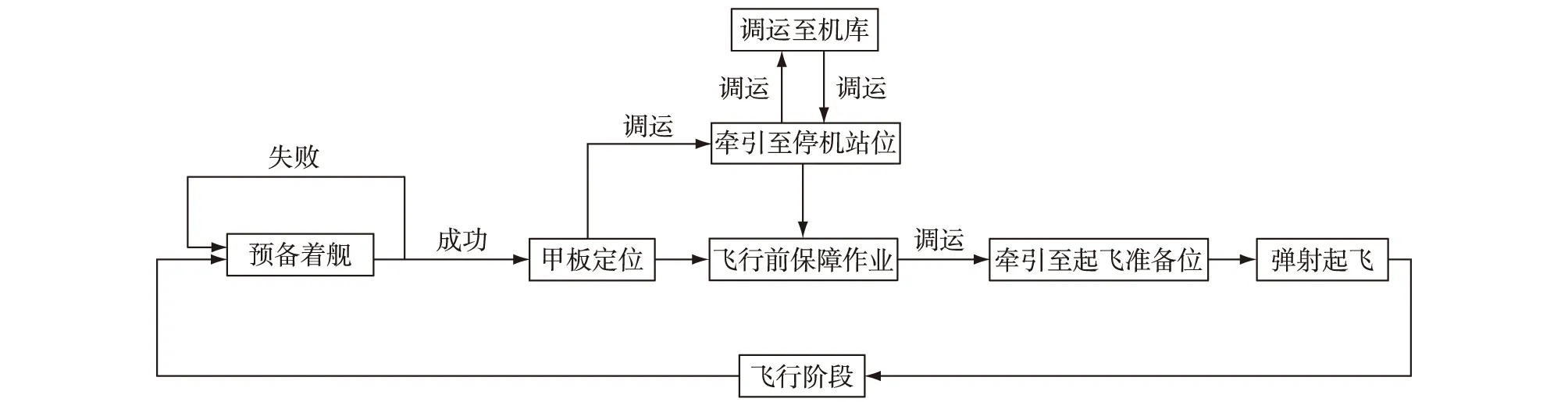
图1 飞行甲板舰载机作业流程

1.2 舰面站位设置

美“尼米兹”级航母飞行甲板长332.8m,最大宽度78.4m,斜角甲板与舰体中心线夹角9.5°。在对飞行甲板建模时,舰岛、弹射起飞装置以及飞行甲板边缘以外部分可视为舰载机调运过程中的永久障碍物予以保留,作出其几何轮廓模型。以左下角某一点为坐标原点,使飞行甲板平面都落入第一象限,x轴水平向右,沿舰艏方向,y轴垂直于x轴向上。作出飞行甲板的外接矩形,飞行甲板上面的永久障碍物等比例画出并定位在坐标系中,并用深色区域表示。出于舰载机回收作业安全考虑,着舰区域仅可设置临时站位节点,将着舰跑道予以标示(宽度20m)。飞行甲板几何模型如图2所示。

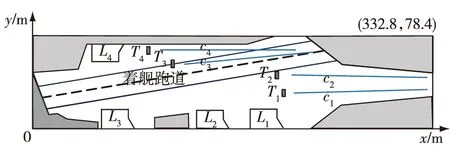
图2 美“尼米兹”级航母飞行甲板几何模型

图2中标有4部弹射器(T1、T2、T3和T4)、4部升降机(L1、L2、L3和L4)以及4条起飞跑道(c1、c2、c3和c4)。

对舰载机进行建模时,根据机型特点,舰载机几何结构模型被表示成简单的平面对称凸多边形,每个平面对称凸多边形由包围舰载机实体边界的线段组成。本文进行舰载机布列时,以舰载机几何中心坐标p(x0,y0)作为其站位点坐标。以“尼米兹”级航母上搭载的舰载机F/A-18为例,F/A-18机长18.31m,机高4.88m,翼展(含翼尖导弹)13.62m,机翼折叠后翼展9.32m[9]。舰载机在飞行甲板调运时,其机翼一般处于折叠状态,以尽可能少地挤占有限的飞行甲板空间,因此F/A-18舰载机及处理后的几何模型如图3(a)-(b)所示。

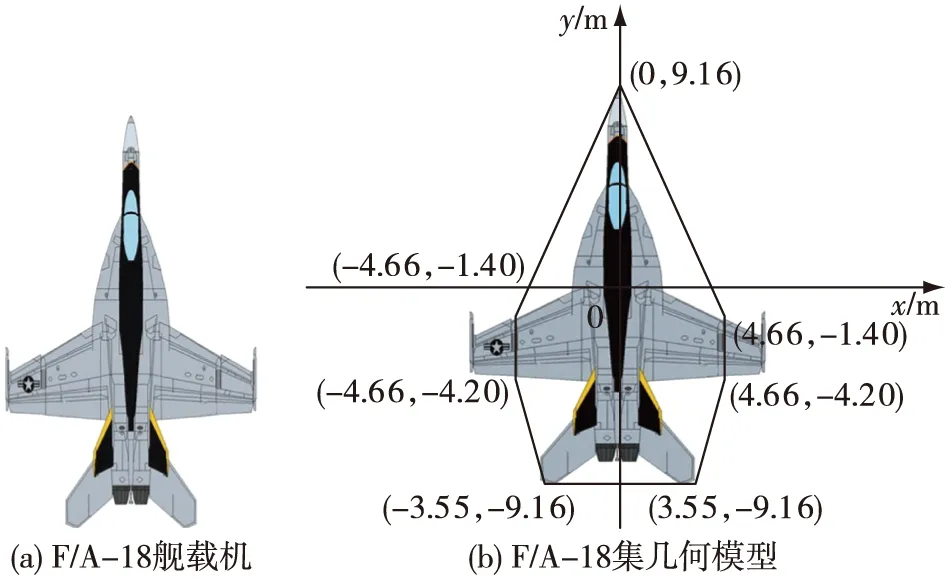
图3 舰载机F/A-18几何建模

舰载机几何模型建立后,需要进行舰载机布列。舰载机布列需要考虑多种因素,如舰体设计结构等。本文在研究舰载机调运作业时,已给定27个主要的F/A-18机型停机站位,同时给出4个起飞准备站位坐标。为方便描述,已对各个站位进行编号,如表1所示。

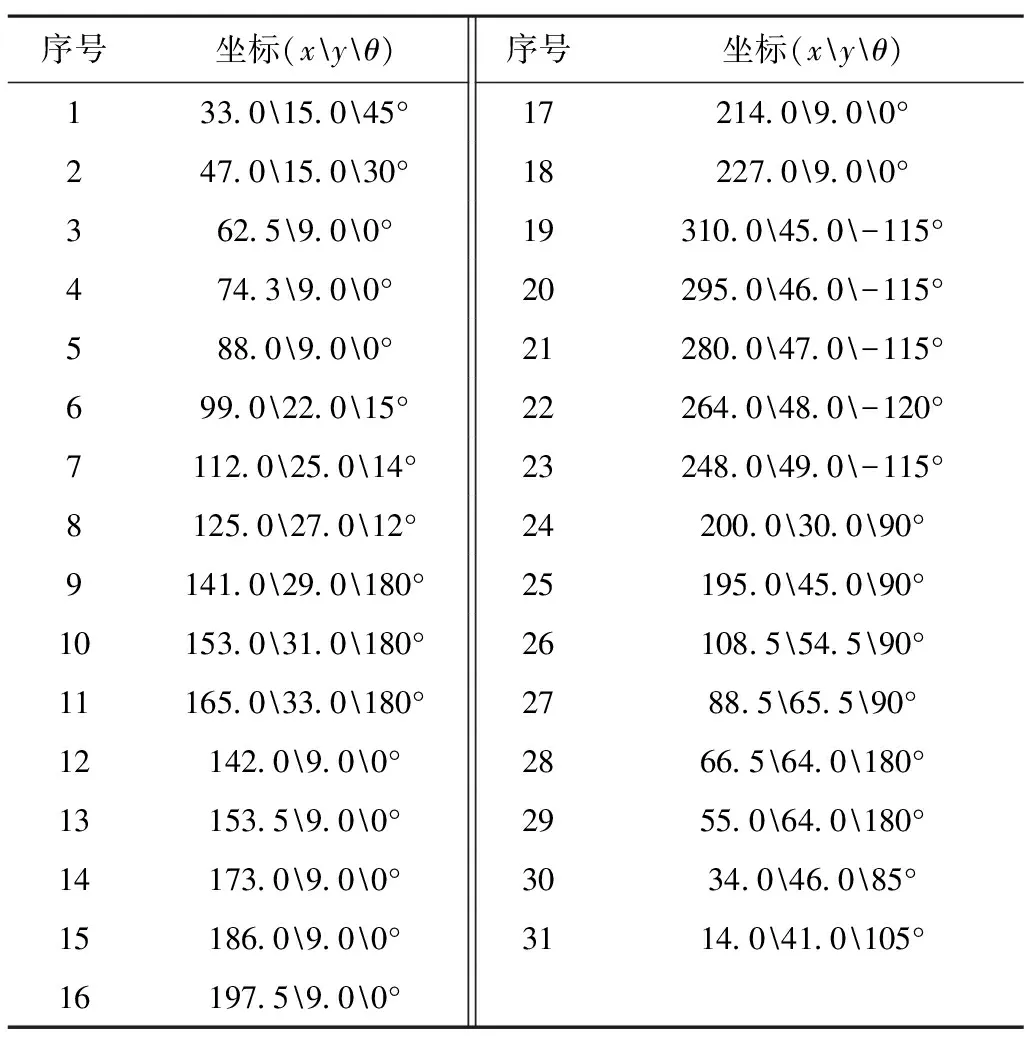
表1 飞行甲板舰载机站位坐标

其中舰载机站位角度为θ(以垂直x轴向上为0°,顺时针为正,逆时针为负,各区分为180°)。舰载机布列如图4所示。

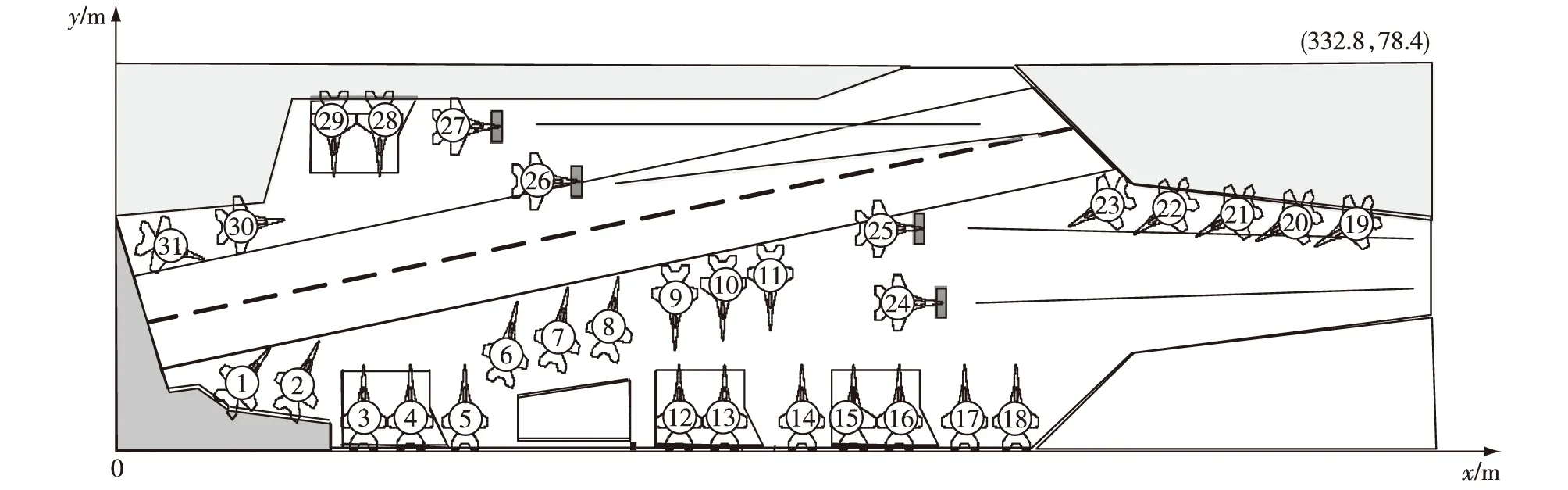
图4 “尼米兹”级航母舰载机布列

其中,24～27号站位即为P1、P2、P3和P4号起飞准备站位(分别对应T1、T2、T3和T4号弹射器),主要为待起飞的舰载机提供暂时待机的位置;其余站位为停机站位,是舰载机可以长时间驻留的地方,用于为舰载机提供停放场所。

2 物流选址

2.1 方法介绍

在物流系统的运作中,物流中心选址是指在一个具有若干供应网点及若干需求网点的经济区域内,选择一个地址设置物流中心的规划过程。较佳的物流中心选址方案是使商品通过物流中心的汇集、中转、分发,直至输送到需求网点的全过程的效益最好。舰载机调运问题属于NP-hard问题,舰载机停机站位作为相对固定节点,与物流配送结点(即客户)有很多相似之处。舰载机调运与物流配送同属于路径规划问题,可借鉴物流中成熟的算法加以解决。

物流选址问题解决步骤如下:

1) 给出目标函数及约束条件;

2) 根据某种评价机制确定候选调运节点;

3) 通过免疫算法从候选节点中选择调运节点;

4) 通过规划得到的路径网络确定舰载机调运路径。

文献[10]给出了物流选址的目标函数及约束条件。在舰载机调运模型中,目标函数是各停机站位到调运节点的距离和为最小,其目标函数为:

(1)

约束条件为:

(2)

Zij≤hj,i∈N,j∈Mi

(3)

(4)

Zij,hj∈{0,1},i∈N,j∈Mi

(5)

其中,N={1,2,…,31}是所有站位的集合;Mi为到调运节点i的距离小于s的候选调运节点集合,i∈N,Mi⊆N;dij表示从站位i到离它最近的调运节点j的距离;Zij为0-1变量,当其为1时,表示停机站位j经调运节点j转运,否则Zij=0;hj是0-1变量,当其为1时,表示点j被选为调运节点;p为被选为调运节点的数量。

2.2 候选调运节点

候选节点是在甲板空间内,按照某种评价机制对甲板区域进行分析,将某些合理的位置坐标放入候选节点序列,以便从中择优选取调运节点。因此本文方法本质上是一种二次寻优的过程。候选调运节点的确定需要进行定性分析,需要考虑一些基础障碍因素,如有明显障碍物(或其他站位舰载机)阻塞位置不应设置候选节点,而且候选节点的选择不可过于集中。本文在设置候选节点时,假设甲板舰载机停机站位布满舰载机。候选节点确定方法如下:

1) 空闲甲板区域充分利用原则。由于甲板空间有限,当甲板布满舰载机时,若不能有效利用甲板空闲区域则很容易导致调运阻塞,此时需要进行倒机操作,这不仅会消耗更多人力,而且会造成调运效率的降低。甲板上着舰跑道的空间较大,且由于舰载机的回收作业,理应设置调运节点,以方便进行回收后的移动定位。因此可将着舰跑道中心线按照一个舰载机身长度c作等长取点,确定其坐标值并将其放入候选节点队列。

2) 升降机和起飞准备站位高频率使用原则。由于这些站位调运作业频繁(升降机用于飞行甲板与机库之间的舰载机转运,起飞准备位为执行起飞作战任务的终端节点),可将其视为已确定的调运节点,同样需将其放入候选节点队列中。

2.3 免疫算法

免疫算法是受生物免疫系统启发,在免疫学理论基础上发展起来的一种新兴智能算法。它利用免疫系统的多样性产生和维持机制来保持群体的多样性,能够求得全局最优解。本文在候选调运节点确定后,采用免疫优化算法求解舰载机调运节点。免疫算法具体实现步骤如下所述，流程如图5所示。

1)识别抗原,将种群信息定义为一个结构体。

2)随机产生N个个体并从记忆库中提取m个个体构成初始抗体群,其中m为记忆库中个体的数量。

3)对上述群体中各个抗体进行评价,同时取前N个个体构成父代群体,取前m个个体存入记忆库中。

4)判断是否满足结束条件,是则结束;反之,则对父代群体进行选择、交叉、变异操作得到新群体,再从记忆库中取出记忆的个体,共同构成新一代群体。转去执行步骤3)。

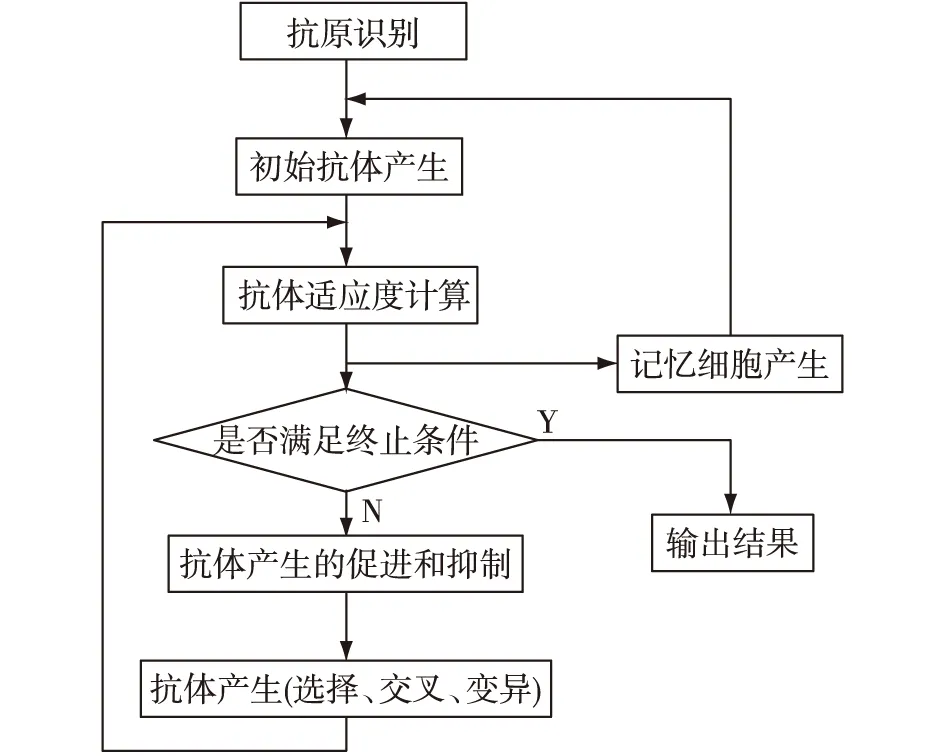
图5 免疫算法流程图

通过免疫算法求解调运节点需要合理给定调运节点数量p,调运节点反应了各停机位舰载机调运移动的分配关系。将得到的调运节点进行连接,则可得到任意两站位之间的路径网络图。对路径网络图进行最优路径搜索,可得到任意两站位之间的调运路径。

3 时序控制

3.1 时序控制方法

舰载机调运作业的难点在于多机出动方面。多机出动的时间要求高,而且涉及四部弹射装置资源的合理分配。因此在保证多架舰载机调运并行进行的同时,需要合理安排调运时序。若调运时序控制不好,则很容易引起调运作业阻塞,这不仅影响到整个任务的出动时间,而且由于对某些资源的占用,将导致后续作业无法进行[11]。在路径网络图中,将所有调运节点作为争夺资源,调运节点之间可作为一个调运阶段。文献[12]提出了一种解决多阶段作业时序安排的有效方法——状态变迁图,通过状态变迁图不仅能够直观地展示出每个阶段作业所耗时间,而且能够进行舰载机调运作业时序分析。本文通过状态变迁图进行多机出动时序控制。

若在某一节点处涉及资源争夺,则通过以下规则进行资源分配:

1) 最短作业优先。当两架以上舰载机同时争夺某一闲置的调运节点资源时,路径较短的舰载机具有优先权。

2) 弹射器负载均衡。分析四部弹射器布局,可大致将四部弹射器分为A(T1和T2)和B(T3和T4)两组,同组内弹射器轮流使用,以减轻单部弹射装置负荷。

3.2 站位距离测量

在确定舰载机调运作业时间之前,需要计算两节点之间的距离。通过物流选址方法确定干线网络后,在调运过程中需要将舰载机停机站位接入调运干线网络。由于舰载机角度不同,而舰载机的朝向对于调运时间的影响不可忽略,本文对其进行了重新建模,采用如图6圆弧计算。

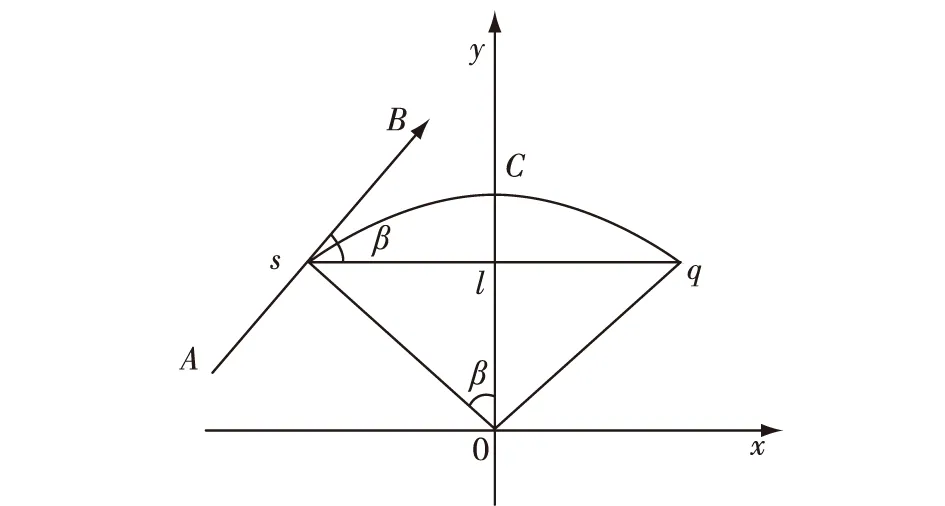
图6 站位距离计算模型

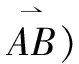
(6)

在舰载机调运移动速度v一定的前提下(设为1m/s),两节点之间调运移动所耗时间与距离长度成正比。

4 仿真验证

经过分析计算,候选调运节点的位置坐标由表2给出,从中选择8个作为舰载机调运节点。

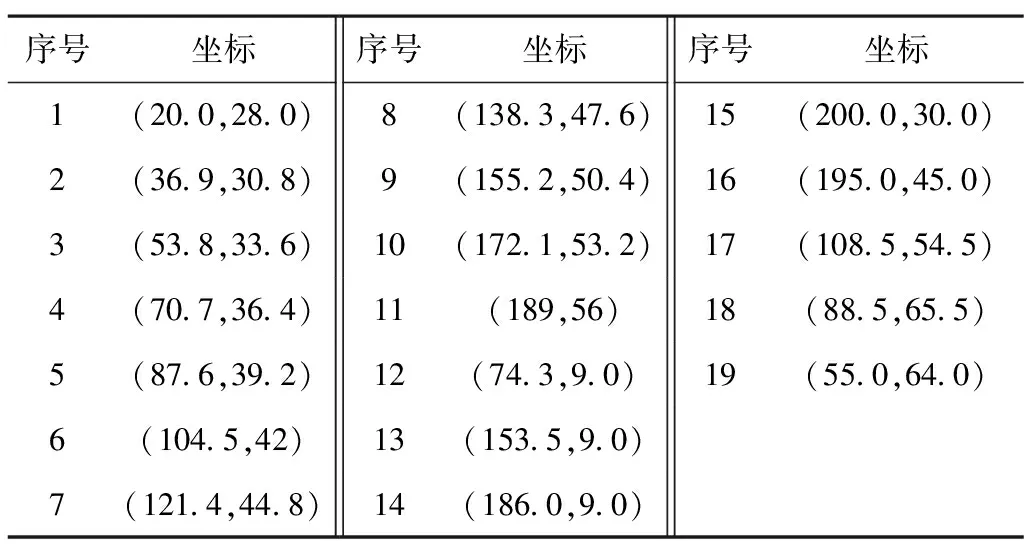
表2 候选节点坐标

根据物流中心选址模型,按照免疫算法步骤进行求解,算法的参数设置为:种群规模为50,记忆库容量为10,迭代次数为100,交叉概率为0.5,变异概率为0.4,多样性评价参数为0.95,求得停机站位与调运节点的分配关系如图7所示。

其中点○表示停机站位,点*表示调运节点。经过计算可得任意两节点之间的距离,舰载机调运路径网络如图8所示。

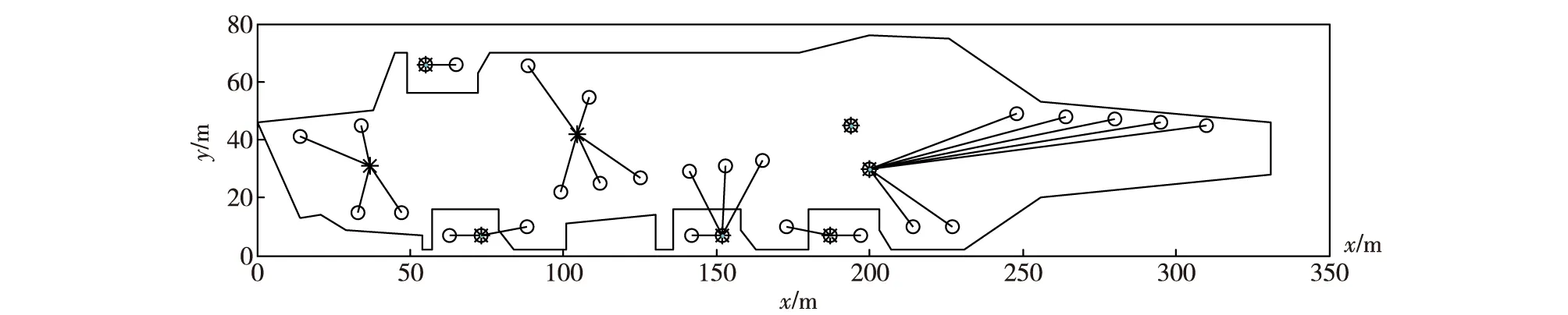
图7 舰载机调运节点模型

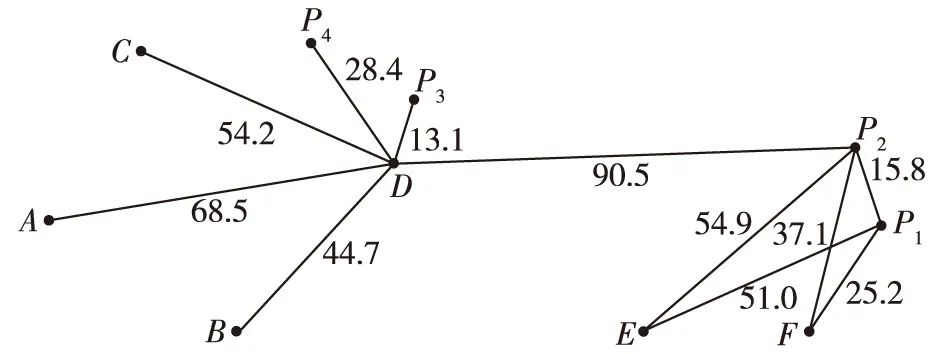
图8 路径网络图

假设某次任务需出动六架舰载机,站位编号及其至最近调运节点的距离(可由式(6)求得)如表3所示。

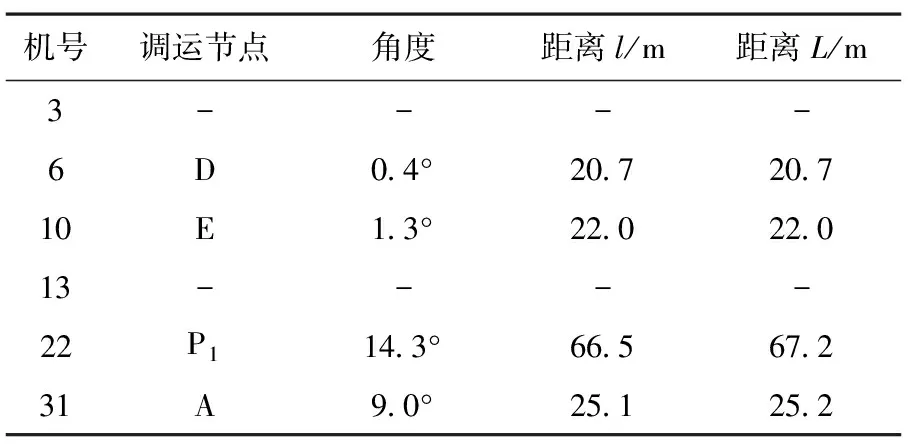
表3 六机站位至最近节点距离

如图9所示,通过状态变迁图分析可知,六架舰载机整个出动时间为147.0s,相比六架机顺序出动,即六架舰载机顺序使用T1、T2、T3和T4号弹射器(所用时间至少为184.2s),能够有效提高调运作业效率。结果表明,通过物流选址方法进行调运节点选择是合理的,能在已知给定的环境中迅速规划出路径网络图,并利用状态变迁图对多架舰载机调运过程进行时序控制。

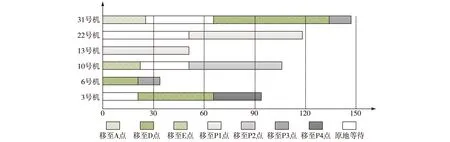
图9 六机出动状态变迁图

5 结束语

本文在对美“尼米兹”级航母飞行甲板环境进行建模的基础上,引入物流选址方法解决舰载机调运作业中的路径规划问题,通过在飞行甲板上设置调运节点,将二维平面内的路径规划问题转化为图论中的最短路径寻优问题,并采用状态变迁图对多机出动调运时序进行控制,为解决飞行甲板舰载机调运问题提供了一种新的思路。结果表明,该方法用于解决航母舰载机调运路径规划问题是可行的,并且能够为其他工程领域的优化问题提供借鉴。

[1] 孙诗南. 现代航空母舰[M]. 上海:上海科学普及出版社,2000.

[2] 司维超,齐玉东,韩维. 基于融合Dijkstra的凸壳算法的舰载机机库调运规划[J]. 系统工程与电子技术,2015,37(3):583-588.

[3] 张智,林圣琳,夏桂华,等. 舰载机甲板调运过程避碰路径规划研究[J]. 哈尔滨工程大学学报,2014,35(1):9-15.

[4] 刘亚杰,李忠猛,陈晓山. 考虑空间约束的机库舰载机调运路径规划方法[J]. 海军工程大学学报,2014,26(3):100-103.

[5] Johnston J S.A feasibility study of a persistent monitoring system for the flight deck of U.S. Navy Aircraft Carriers[D].California:Air University,2009.

[6] Ryan J C.Assessing the performance of human-automation collaborative planning systems[D].Cambridge,Massachusetts State:Massachusetts Institute of Technology,2011.

[7] 杨炳恒,韩峰,王海东,等. 舰载机机库调运作业路径[J]. 舰船科学技术,2012,34(8):141-143.

[8] 刘亚杰,李忠猛,谢君. 基于Petri网的舰载机出库调度建模方法[J]. 火力与指挥控制,2015,40(9):152-156.

[9] 吕开东,朱齐丹,李新飞.舰载机航空保障需求及排队网络模型研究[J].飞行力学,2014,32(1):88-92.

[10]史峰. MATLAB智能算法30个案例分析[M]. 北京:北京航空航天大学出版社,2011.

[11]司维超,韩维,宋岩. 面向任务T-Petri网的舰载机出动流程仿真[J]. 计算机工程与应用,2014,50(16):237-242.

[12]谢君,傅冰,鲍敬源. 基于状态变迁图的舰载机出动能力分析[J]. 中国舰船研究,2014,9(2):1-5.

An Application of the Logistics Center Location to the Carrier-borne Aircrafts Transportation on Flight Deck

LI Xiao-jie,XIE Jun,FU Bing

(College of Electronic Engineering,Naval University of Engineering,Wuhan 430033,China)

In order to improve the efficiency of transferring carrier-borne aircrafts on the flight deck, the logistics center location method is introduced to solve the path planning problem of carrier-borne aircrafts. Aimed at the complexity of the flight deck environment and the problem of the shapes of carrier-borne aircrafts can’t be ignored, the Nimitz class aircraft carrier is taken as the research object, firstly the flight deck and carrier-borne aircrafts are modeled geometrically, then using the logistics center location method, a number of candidate transportation nodes are set up on the flight deck through a certain evaluation mechanism, and the immune algorithm is used to optimally select the candidate transportation nodes and then the transportation path network is determined, finally the multiple aircrafts transportation timing is controlled by state transition diagram. The simulation result of six aircrafts dispatching operation show that the proposed method is simple and reasonable, and can provide decision-making reference for carrier-borne aircrafts transportation management staff.

carrier-borne aircrafts transportation; logistics center location; immune algorithm; timing control; state transition diagram

2016-08-31

2016-11-09

李晓杰(1991-)，男，山东德州人，硕士研究生，研究方向为作战系统工程。 谢 君(1973-)，女，博士，副教授。 傅 冰(1979-)，男，博士研究生，讲师。

1673-3819(2017)02-0129-06

U674.771；E917

A

10.3969/j.issn.1673-3819.2017.02.024