重型车辆的气压制动能量回收的建模及仿真分析
2019-03-06
(北京信息科技大学 机电学院 北京 100192)
引言
环境污染和能源消耗问题推动了重型车辆节能化及再利用问题的发展。制动能量回收的能量利用率是研究重型车辆的重中之重。当重型车辆在制动工况下由于摩擦力的作用,致使车辆的动能转化为热能,样于人类的可持续发展。因此会带来以下问题:(1)重型车辆在下坡时能量没有得到充分利用并且当期强制怠速时会造成大量的燃油消耗。(2)重型车辆在制动时会产生较多的废气,这些废气会对人们的身体健康带来损害。(3)为了提高重型车辆的安全效能可以勤于换摩擦元件、改善摩擦片之间的间隙,这样可以降低由于制动器的损害而带来的给人身带来的威胁。
本文对重型车辆的气压制动能量回收系统在Simulink中对各模块建立仿真模型及仿真研究,最后对仿真结果进行理论分析。
一、气压制动能量回收仿真模型
(一)三大系统简介
为了研究气压制动能量回收系统,首先要建立系统仿真模型。本章首先对车辆动力学特性和气动马达排量调节特性进行数学分析,然后基于 MATLAB 搭建整车动力学模型以及气压制动能量回收系统模型。
重型车辆联合制动系统可分为三大部分,即气压动力制动系统、动力分配系统、再生制动系统[1]。

图1 联合制动系统原理图
(1)气压动力制动系统
气压动力制动系统主要由储气罐、电子踏板、制动阀以及制动器等组成。在制动工况下,控制器根据车速和制动强度以及再生储气罐SOC计算需求制动力矩,并将需求制动力矩信号发送给制动阀,控制阀口开口面积进而对实际制动力矩进行线性控制,对车辆进行制动。
(2)制动能量回收系统
制动能量系统由再生制动储气罐、二次元件(气泵/气动马达)、单向阀以及扭矩耦合器等。由车辆制动时车轮的惯性力矩带动空气压缩机转动,将储气罐中的气压能充入再生储气罐中,实现了能量的转化过程。
(3)动力调节系统
动力调节系统主要由电磁换向阀、储气罐、再生储气罐、空气压缩机组成。重型车辆进行制动后,储气罐气压会下降,再生储气罐气压会升高,当储气罐压力到达其最低工作压力时,电磁换向阀会打开,再生储气罐会为储气罐进行充气;
(二)气动力制动系统
气压动力制动系统主要由电子踏板1、电子控制单元2和3、储气罐8、空气减压阀4和5、制动气室6和7等元件组成。

1-电子踏板;2、3-电子控制单元;4、5-前、后轮空气减压阀;6、7-前、后轮制动气室;8-储气罐;
工作原理为:驾驶员有制动意图后踩下电子踏板1,电子踏板上的转角传感器采集其转角信号,并将此转角信号转化为电压信号,通过电子控制单元2和3转为电流信号,并传送到空气减压阀4和5上,电流通过电磁线圈时,产生电磁力推动阀芯克服弹簧弹力产生位移,从而使得储气罐里的气压能进入制动气室产生制动压力,通过制动摩擦片对车辆进行制动。
1.气压动力制动系统的数学模型
(1)空气压缩机数学模型
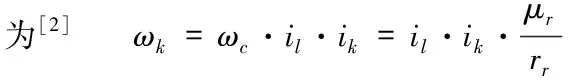
(4.1)
式中,ωk—运输车辆的车轮角速度;il—半轴到气动离合器的传动比;
ik—气动离合器到空气压缩机的传动比;
可以知道,空气压缩机的流量为:
(4.2)
式中,Vm—空气压缩机的排量;nk—空气压缩机的转速,r/min。
把式(4-1)和式(4-2)代入式(4-3)得:
(4.3)

(4.4)
(2)制动气室的数学模型

(4.7)

(4.8)
式中,P1表示制动气室左侧腔内的压力,S0表示膜片承压面积,k表示回位弹簧刚度,x表示推杆的位移。
(4.9)
其中,R1,R2分别为膜片内外半径;μ为摩擦系数,F为活塞推力;δ为扇形角。
(4.10)
其中,Vz为制动气室容积;Ez为制动气室的等效体积弹性模量。
(3)储气罐的数学模型
储气罐充放气过程,可认为是绝热过程,可知储气罐排气的流量方程为
(2.10)
式中,p0是储气罐的充气压力;V0是储气罐的有效容积;pA是储气罐的最高工作压力;n为热力学常数,取n=1.4;p1是储气罐的出口压力。
(三)制动能量回收系统
1.柱塞式气泵/气动马达的数学模型
气泵/气动马达的排量表达式为[3]
(4.15)
再生制动力矩表达式为
(4.16)
气泵/气功马达的流量表达式为
(4.17)
式中,V是气泵/气动马达的排量(ml/r);d是柱塞直径(m);Z是柱塞数量;y是活塞位移(m),λ是斜盘倾角与活塞位移增益(rad/m);Δ P —气泵/气动马达进出口压力差,(MPa);n—气泵/气动马达转速,(r/min)。
2.再生储气罐的数学模型
(4.18)
式中,p0是再生储气罐的充气压力;V0为再生储气罐的有效容积;n为气体的多变过程指数,取n=1;p为再生储气罐的出口压力;
(三)动力调节系统
动力调节系统主要包括储气罐、再生储气罐及电磁换向阀。储气罐和再生制动储气罐数学模型前面已介绍,下面主要建立电磁换向阀的数学模型。
电磁换向阀的数学模型:
(1)电磁换向阀的受力分析
根据牛顿运动定理,当电磁换向阀通电时阀芯的运动方程为:
(4.31)
式中,m—阀芯质量;x—阀芯位移;
c—阀芯运动时的等效粘性阻尼(N·s/m);
xp—恢复弹簧预紧量(m);Fe—电磁吸力(N);
p—阀芯所受的气体压强(Pa);A0—阀芯的横截面积(m2);
K—弹簧刚度。
气压电磁阀的动态特性能 够通过制动气室的压力变化来反映,因此研究电磁阀和制动气室之间的压力动态特性十分重要。
气压的制动过程包括两个阶段:电磁阀的开关动作和制动气室的充放气。所以本文采用物理方法来建立制动气室充放气过程的数学模型,并在此基础上重点研究电磁阀的动态特性的压力动特性的影响。
对于充气过程,根据气体连续性方程,气体通过制动气室入口小孔的瞬时流量可表达为:
(4.32)

A1—气室入口截面积,A1=1.26×10-5m2;
R0—气体常数,空气:R0=287.1J/kg·K;
K—绝热指数,K=4.1;
T1—气室中气体的绝对温度,T1=313K;
P1、P2—分别为气室入口上、下游的压力(pa)。
理想气体状态方程符合下述关系:
(4.33)
式中:p—压力(pa);Qm—气体流量(m3/s);
V—气室容积,V= 1×10-3m3。
二、气压制动能量回收仿真分析
(一)气压动力制动系统仿真分析
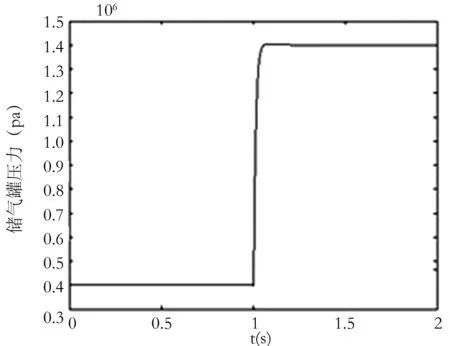
图3 储气罐的压力变化曲线
说明储气罐的压力1s时不变,当1s之后增加至1.4MPa,然后1s之后趋于稳定。
(二)制动能量回收系统仿真分析
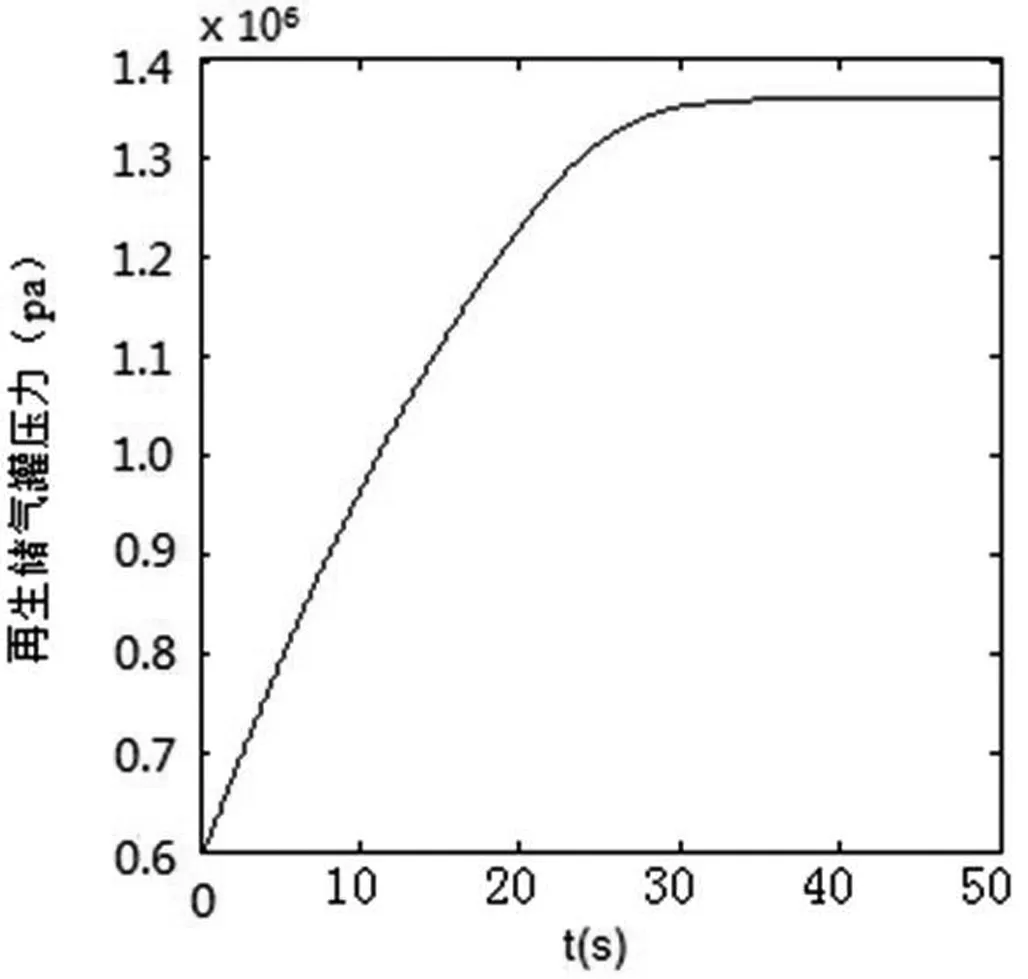
图4 再生储气罐的压力变化曲线
说明再生储气罐压力从初始0.6MPa逐渐升高至1.35MPa,直到70s之后,压力不变。
(三)动力调节系统仿真分析

图5 储气罐压力仿真曲线
说明储气罐压力从初始1.4MPa逐渐降低至0.5MPa,直到60s之后,压力保持不变。
三、结束语
本论文对气压制动能量回收系统进行了选型及参数匹配、控制策略的相关研究以及对重型车辆的气压制动能量回收的数学建模及simulink仿真分析。本论文主要进行了以下研究:
(1)对传统气压制动系统的介绍和分析,逐步了解其优势和弊端。并且对重型车辆的气压制动能量回收系统的结构进行设计。
(2)对气压制动能量回收系统的关键元件进行选型与参数匹配,根据关键元件的主要性能参数,可大致确定关键元件的参数范围及其型号。
(3)对重型车辆的气压制动能量回收系统在Simulink中对各模块建立仿真模型及仿真研究,最后对仿真结果进行理论分析。
