立体几何复习要点例析*

2019-03-06

中学教研(数学) 2019年3期

关键词：棱柱三视图考点

●

(学军中学，浙江杭州 310012)

●石磊

(永康外国语学校，浙江永康 321300)

1 考点回顾

进入文理合卷以来，浙江省数学高考对立体几何内容的考查回到传统的点、线、面关系，重点考查三视图(如2018年第3题、2017年第3题)，二面角(如2018年第8题、2017年第9题),平行、垂直和线面角(如2017年第19题、2018年第19题).立体几何问题一般都是通过传统的几何背景(棱柱、棱锥等)设置问题，叙述简洁，入口宽，方法活.浙江省数学高考的立体几何问题很好地考查了学生的直观思维、逻辑推理和数学抽象等核心素养[1].

正因为如此，高三立体几何复习要强化学生对基本概念的理解、基本定理的运用，要通过四面体、正方体等学生熟悉的背景，构建学生熟悉的知识框架，强化转化、折叠和旋转等策略，提升学生分析问题和解决问题的能力.另外浙江省数学高考对向量法解决几何问题的要求降低，连续两年都是界定在了解层次.

2 典题剖析

考点1空间的点、直线和平面的位置关系判断.

例1设a,b是两条不重合直线，α,β是两个不重合平面，则“a⊥b”成立的一个充分条件是

( )

A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥β

C.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β

(2018年浙江省五校第二次数学联考试题第3题)

分析正确选项为C.因为b⊥β,α∥β,所以b⊥α.又a⊆α,从而a⊥b.其他选项均不能说明a⊥b.

评注进入文理合卷以来，浙江省数学高考对空间点、直线和平面的考查比较常规，要求考生掌握空间直线和平面位置的相关知识点，比如空间直线平行及垂直、直线和平面平行及垂直、平面和平面平行及垂直相关的判定定理和性质定理.在复习中，不要盲目拔高，通过一轮复习引领学生构建立体几何的知识体系，尤其是定理成立的条件等[2].

考点2三视图、空间几何体的结构.

例2空间一个几何体的三视图如图1所示，其中正视图和侧视图为全等的矩形(边长为3 cm和2 cm)，俯视图为正方形(边长为2 cm)，则该几何体的表面积为______cm2,体积为______cm3.

(2016年浙江省名校协作体高三年级数学试题第10题)

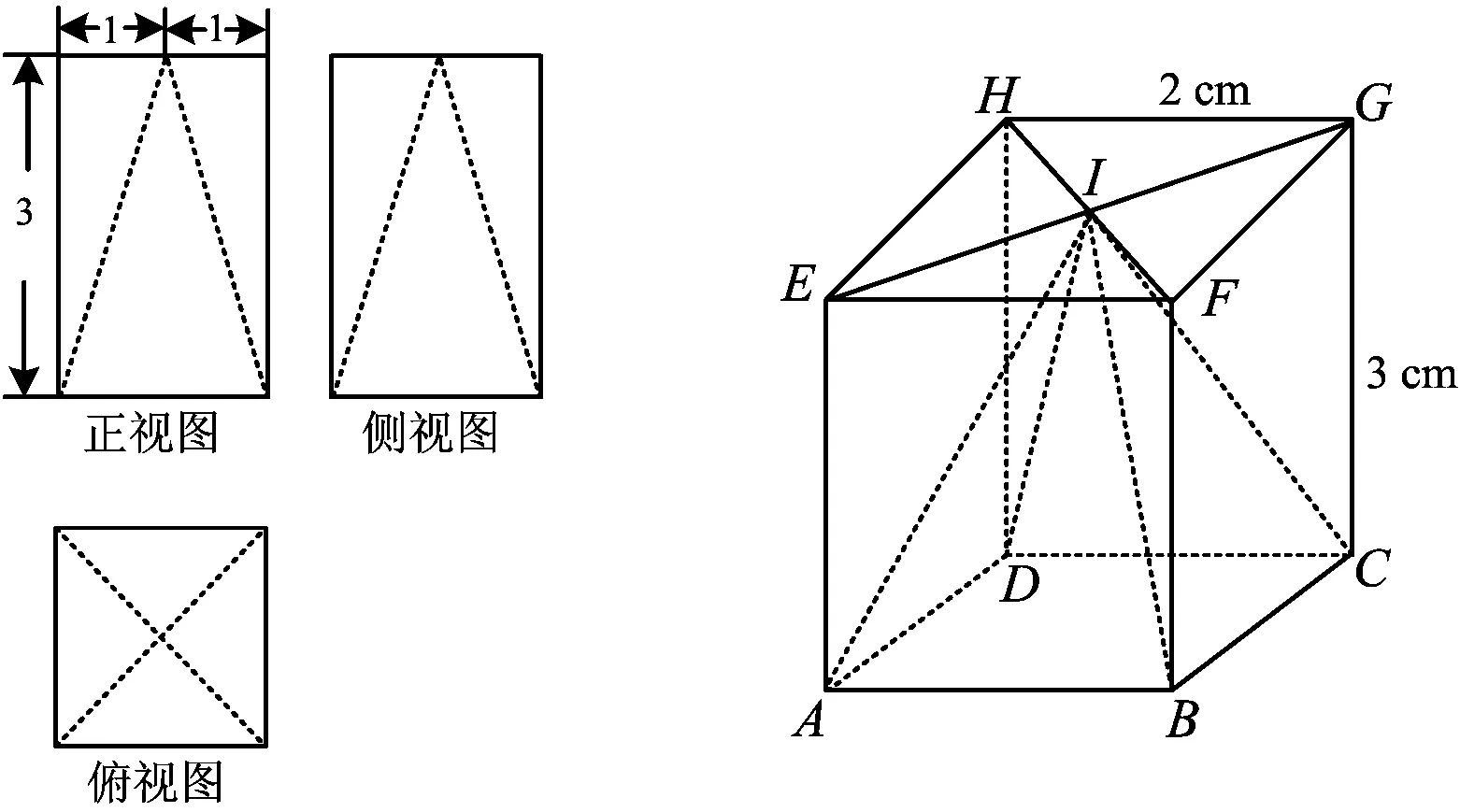
图1 图2

分析根据三视图的特征，可以判断出空间几何体的特征：一个长方体挖去一个四棱锥I-ABCD(如图2),从而

评注三视图还原为空间几何体是一个从平面到空间的想象过程，是非常好的立体几何考查知识模块，是考试的热点和重点之一.对于学生来说，这是个难点，需要重点关注[3].在高三的复习中，要重视三视图还原空间几何体和利用空间几何体画三视图的培养.另外三视图的考查，常常把空间几何体的表面积和体积结合起来，计算起来有时容易算错，这个要注意.

考点3空间角的求法,重点是直线和平面所成的角.

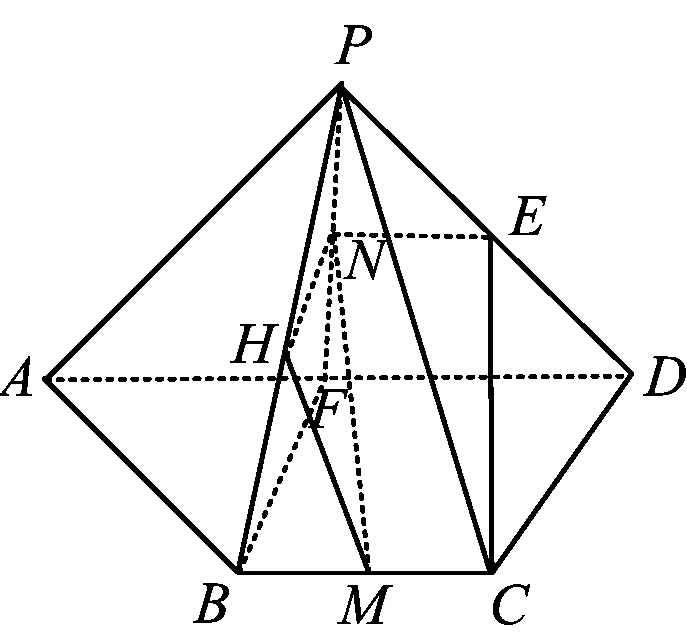
图3

例3如图3，在四棱锥P-ABCD中，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD,PC=AD=2DC=2CB,E为PD的中点，求直线CE与平面PBC所成角的正弦值.

(2017年浙江省数学高考理科试题第19题改编)

思路1分别取AD，BC和PF中点F,M和N,则MN∥CE，于是原问题转化为求MN与平面PBC所成的角.作NH⊥PB于点H，联结HM，可证明∠HMN为所求线面角的平面角.

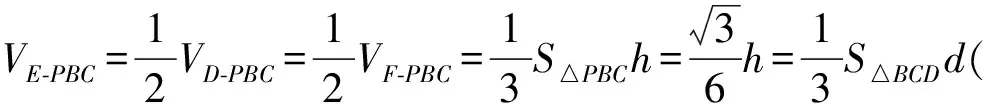
评注本题颇有特色，体现了浙江省数学高考试题简洁且富有思维的特色，淡化计算和技巧，重视回归传统.本题可以直接作角，也可以进行等积变换来处理，考查了学生的转化和降维思想.

图4

例4如图4，在多面体ABC-A1B1C1中，AA1，BB1，CC1均垂直于平面ABC，∠ABC=120°，AA1=4，CC1=1，AB=BC=BB1=2，求直线AC1与平面ABB1所成角的正弦值.

(2018年浙江省数学高考试题第19题改编)

评注本题仍为传统背景下的几何问题，考查点、线、面的位置关系和空间角的掌握情况，只需简单地进行图形转化，寻找平面的垂线.该题在简约中体现特色，在直观思维中寻找转化的策略.

图5

考点4折叠问题.

例5如图5，在矩形ABCD中，AE=EB=AF=4，FD=6，沿着EF将△AEF翻折到△A′EF,并且有平面A′EF⊥平面BEF，沿折痕MN(其中点M在AD上，点N在BC上)将四边形MNCD向上翻折，若使得点C与点A′重合，求MF的长.

(2010年浙江省数学高考理科试题第20题改编)

评注折叠和展开问题是浙江省数学高考的热点和重点.折叠是从平面到空间，折叠后的不变量是解决问题的关键.“如何寻找不变量，如何进行问题的转化”很好地反映了学生的直观思维能力.

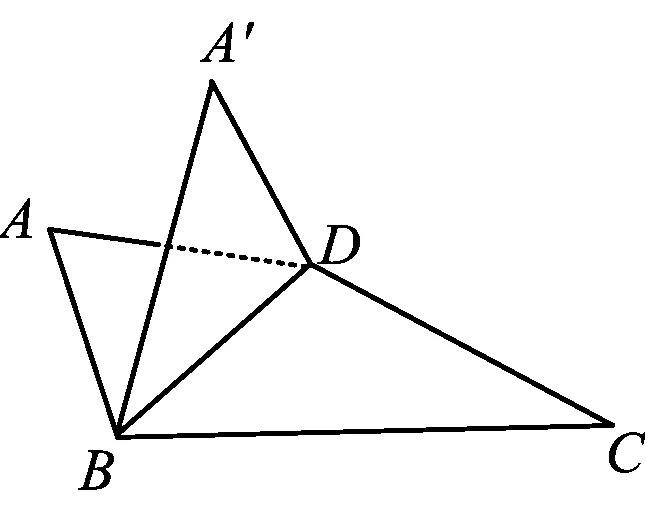
图6

考点5旋转问题.

图7 图8

评注旋转问题一直是立体几何的难点和热点，“在旋转过程中哪些量没有发生改变”是解决问题的关键，也是学生处理这一类问题的难点.本题通过分析典型的圆锥模型，找到突破口.实际上,通过此类问题的分析和解决，可以有效地提升学生的抽象思维能力和直观想象能力.

3 精题集萃

1.已知两条异面直线a,b所成的角为70°，P为空间一点，则过点P与a,b都成70°的直线c有( )条

A.1 B.2 C.3 D.4

2.根据以下条件能判断直线a∥平面α的是

( )

A.a∥b,b⊂αB.a∥b,b∥α

C.a∥β,β∥αD.β∥α,a⊂β

3.某几何体的三视图如图9所示，则该几何体的体积为______,表面积为______.

图9 图10

4.如图10,在直角梯形ABCD中，AB∥CD,AB⊥BC,2AB=CD=2,现将△ADC沿AC折成三棱锥P-ABC.当二面角P-AC-B的大小为60°时，PB=______.

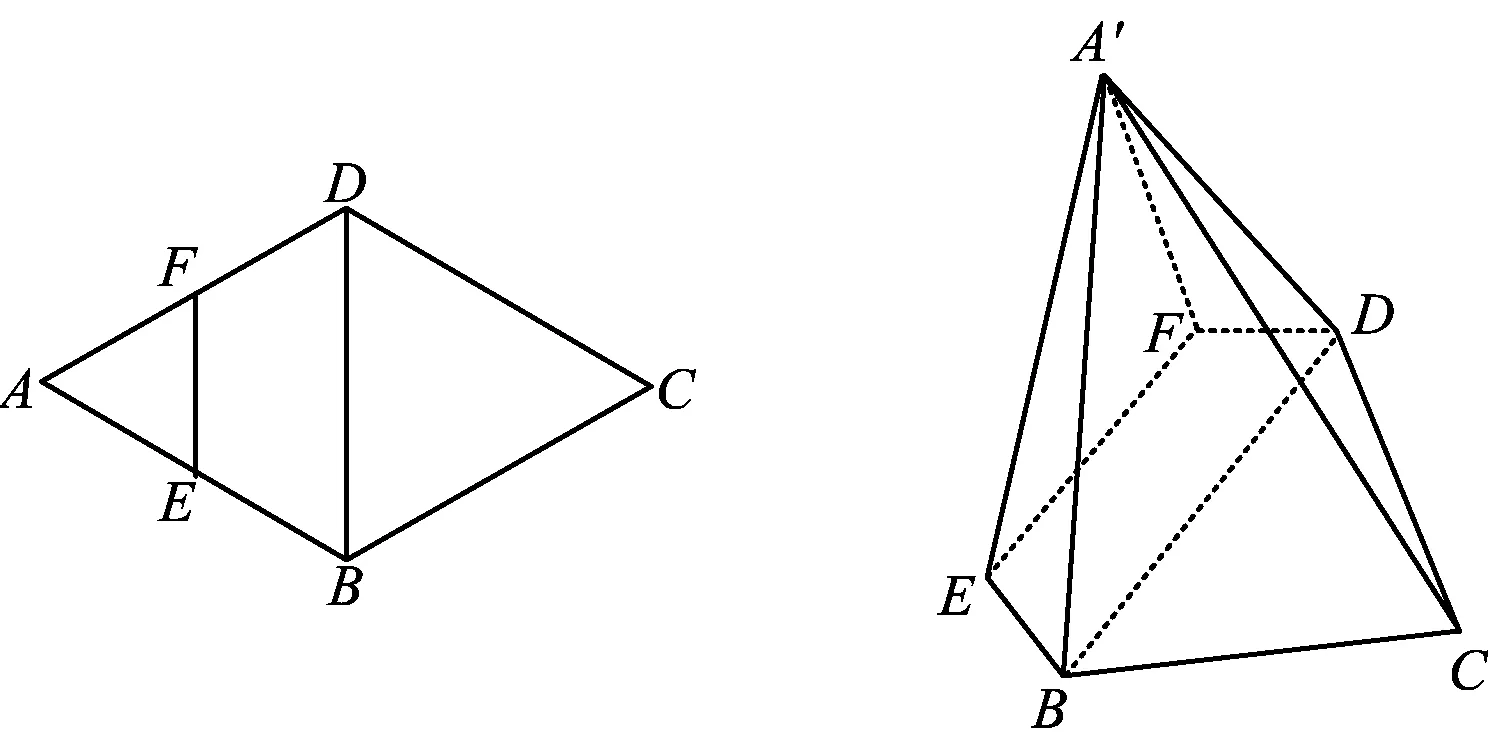
图11

6.如图12，在三棱柱ABC-A1B1C1中，上、下底面是边长均为1的正三角形，侧棱长为2，P为棱AB的中点.

1)证明：AC1∥平面B1CP;

2)若三棱柱ABC-A1B1C1为直棱柱，求侧棱A1A所在直线与平面B1CP所成角的正弦值.

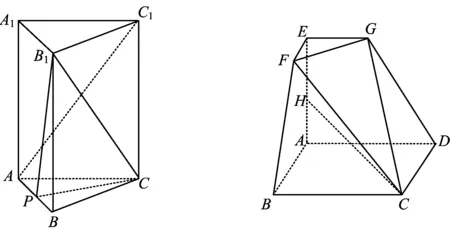
图12 图13

7.在如图13所示的空间几何体EFG-ABCD中，四边形ABCD是边长为2的正方形，AE⊥平面ABCD，EF∥AB，EG∥AD，EF=EG=1，AE=3，点H为棱AE上一动点.

1)求证：HC⊥FG；

2)当二面角H-FG-C为直二面角时，求HC与平面GCD所成角θ的正弦值.

参考答案

6.1)证明如图14，取A1B1的中点E，联结C1E,AE.易证明面AC1E∥面B1CP,从而AC1∥平面B1CP.

图14 图15

2)解因为A1A∥B1B,所以A1A与面B1CP所成的角即是B1B与面B1CP所成的角.在直棱柱中，面ABB1A1⊥面ABC，面ABB1A1∩面ABC=AB，CP⊥AB，CP⊂面ABC，从而CP⊥面ABB1A1，于是面B1CP⊥面ABB1A1.如图15，作BQ⊥B1P于点Q，根据面面垂直的性质定理可知BQ⊥面B1PC.因此，∠QB1B即为所求直线B1B与面B1CP所成角的平面角，故

7.1)证明如图19,联结AC,BD,交于点O.取AB,AD的中点M，N,联结FM,GN.易证GF⊥AC,因为GF⊥EA,AC∩EA=A,从而GF⊥面EAC，又GH⊂面EAC，故GF⊥CH.