教学生会思考 落实核心素养*——一道高三模考试题的评析与思考

●

(南京市第二十九中学,江苏 南京 210036)

●张云飞

(南京市第十二中学,江苏 南京 210011)

《普通高中数学课程标准(2017年版)》(以下简称《新课标》)指出：高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质.数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这6个素养既相互独立、又相互交融，是一个有机的整体.章建跃博士曾指出：核心素养是在复杂情景中解决问题的能力和品格，是个体与情景的持续活动中通过不断解决问题、创生意义而形成的.同样地，数学核心素养的形成是以数学知识为载体，以数学活动为路径而实现的.

面对高三较难习题的教学，作为一线教师在平时的教学中不仅要认真体会和感悟《新课标》带来的变化，更应该思考：如何在高三的习题教学课堂中落实核心素养，如何让以核心素养为导向的高三数学习题教学课堂更高效？那就是要教会学生思考.学生是学习的主体，一定要让学生的思维“活”起来，提倡独立思考、自主学习、合作交流等多种学习方式，提高学生学习数学的积极性.同时，教师要适时给予学生引导和帮助，为学生创设问题情景，让学生高度参与课堂、融入课堂，培养学生从数学的视角发现问题、提出问题并分析和解决问题的能力，感受数学化的过程，体会数学课所带来的数学“味”，那就是“思维”.只有教会学生思考，才能让学生达到“深度”学习，才能让学习“真正”发生，才会让核心素养落到实处.下面结合一道高三模考试题的解析，谈谈数学核心素养的落实.

1 案例呈现

作为填空压轴题,它究竟难在哪里，它反映的是哪一类问题，你会选择哪种方式化解这类问题的难点，题目中能否找到一些具有暗示作用的信息，你是否使用了题目中所有的条件，各个条件之间的关系是否存在一定的关联，如何自然地帮助和指导学生进行解题……通过这些问题的分析和讲评，教会学生思考，让学生学会思考.

2 解法探究

解法1取AC的中点，化不等为相等.

图1

从而

又P为线段BC上任意一点，且恒有

从而

PD2≥P0D2.

tan(∠BAF+∠CAF)=-3，

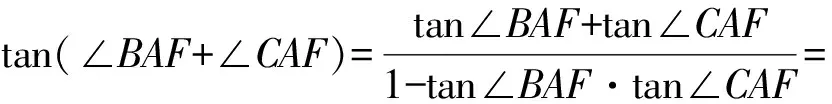
因此

解之得

故

对于该题难点的突破，教师在讲评时可以引导学生从以下3个方面进行尝试.

尝试1联想极化恒等式.

由 (a+b)2=a2+2a·b+b2,

(1)

学生自然会联想到

(a-b)2=a2-2a·b+b2,

(2)

式(1)+式(2)，得

(a+b)2+(a-b)2=2(a2+b2),

(3)

式(1)-式(2)，得

(4)

师：你能从几何的视角刻画式(3)和式(4)吗？

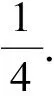
尝试2联想向量的投影.

对于难点的突破，学生最有可能想到的是向量数量积的定义，即

师：下一步如何思考？

对学生而言，这是一个思维上的挑战，教师应鼓励学生独立思考、敢于尝试.他们可能尝试使用余弦定理，遇到障碍时教师应适时给予提示，让学生“以退求进”也许会有新的发现.教师要学会等待，给学生思考的时间和空间，发挥学生学习的积极性，培养学生勇于探索、严谨求实的科学精神，让学生经历知识发生、发展的过程，深化对概念的理解，才能达到对知识的灵活应用.

让学生回归课本，复习苏教版《数学(必修4)》第77页的链接“向量b在向量a方向上的投影”，会为该题的求解带来全新的想法：如图1，过点A作AF⊥BC于点F，设∠APC=α，当点P在线段CF上时，

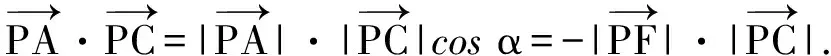
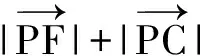
即

高三的复习不是简单的重复，而是在原有的基础上对知识再开发、再认识、再提高和再应用的过程.课本是复习的首要资料，不但要细致而且要做到全面不留死角，通过复习让学过的知识连成线、结成网，打通各知识点间的联系，不断为学生创造探究的点，能够在原有认知的基础上提升学生的元认知水平.

尝试3联想向量数量积圆.

x2+y2-cx=λ，

即

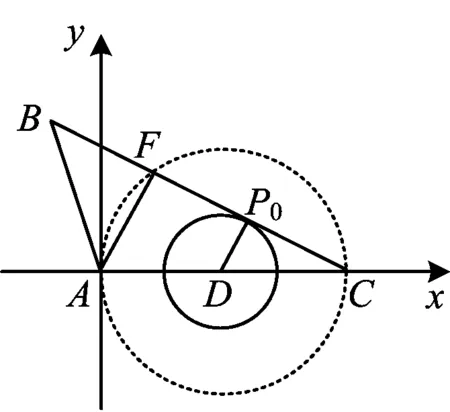
图2

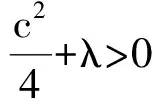
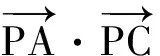
为什么会想到隐圆⊙D，是如何想到的，还存在哪些与向量相关的隐圆……这些设问都是教师为学生创设的探究背景，启发其思路，进而探究规律.另外，教师要注重信息技术与数学课程的深度融合，实现传统教学手段难以达到的效果，从而得以转变教学与学习的方式.比如，借助几何画板对隐圆⊙D的动态分析，可以把原本很抽象的知识变得直观形象，更易于学生理解和接受.在这个难点突破的过程中，让学生下意识地积累数学基本活动经验，从而促进学生思维能力、实践能力和创新意识的发展，也为培养数学核心素养奠定基础.

图3

解法2建立直角坐标系.

以点A为坐标原点、AC所在的直线为x轴建立如图3所示的平面直角坐标系xAy，由tanA=-3易得直线AB的方程为y=-3x(其中x≤0).设B(x0,-3x0),C(a,0)，由

得

即

(x0-a,-3x0)=3(x1-a,y1)，

从而

因为P0D⊥BC，所以

即

又

解之得

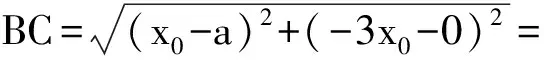
解法3建立斜坐标系，转化为二次函数求解.

图4

又由S△ABC=1，得

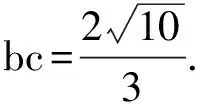
(5)

由P为线段BC上任意一点，且恒有

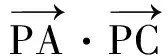
(6)

(7)

联立式(5)和式(7)，得

3 探根寻源

( )

A.∠ABC=90° B.∠BAC=90°

C.AC=ABD.AC=BC

(2013年浙江省数学高考理科试题第7题)

例1来源于例2的改编，教师要揣摩命题者的意图以及该题所要考查的内容，如通过该题的考查需要达到什么样的目标，要解决这个问题需要学生掌握哪些知识和技能，为了更好地解决这个问题是否要作一些知识的拓展.建议教师可以先让学生自己研究例2，让学生思考：考查的是什么内容、切入点是什么、难点是什么、采取何种方式破解难点、渗透了哪些数学思想和方法、是否存在求解问题的通性通法等.教师精心备课，设计好问题，才能让学生经历探索和发现的过程并学会思考.

4 案例反思

数学的6个核心素养不是孤立的，而是相互联系和渗透的一个整体，是通过学生学习而逐步形成的正确价值观念、必备品格和关键能力.数学课堂为数学核心素养的落实提供了必备的环境，落实数学核心素养要体现4个方面：情景与问题、知识与技能、思维与表达、交流与反思.只有教会学生如何思考问题，才能更好地践行核心素养，才能真正地将核心素养落在实处.

4.1 关注“四基”，提升核心素养

“四基”(即基础知识、基本技能、基本思想、基本活动经验)是《新课标》的课程目标之一，“四基”是培养学生核心素养的基石，是获得进一步学习和实现“四能”的必备能力，也是突破较难习题所具有的关键能力.俗话说：基础不牢，地动山摇.只有扎实地构筑和巩固基础知识，并掌握解决问题的常规方法和技巧，才能在一题多解中培养学生的选择能力和对新问题的把控能力，才能教会学生思考.

4.2 问题“引领”，教会学生思考

美国数学家哈尔莫斯曾经说过：问题是数学的心脏，是数学思想的源泉，是数学思维的动力.要想让学生的思维得到持续性发展，就必须培养学生的问题意识，进而提升学生提出问题的能力，更重要的是让学生学会思考.

怎样才能较好地引领学生思考呢？比如对于较难的习题，一定要找到学生的痛点是什么、如何将难点进行分解、如何将学生思维的“痛点”变成他们探究的“兴奋点”……这不仅需要学生有扎实的基本功，更需要教师的问题引领，用好提示语引导学生思考，比如它是一类什么问题、要求或要证的目标是什么、这个目标究竟指的是什么意思、要解决这个问题需要什么材料、材料是直接的还是间接的、如何用数学的方式呈现这些材料、为什么这样想、为什么这么做、你是怎么想到的、你是否还有其他的想法等.鼓励学生去不断尝试，不要害怕失败，只有坚持才能取得成功.如果学生离开了教师也能这么想问题的话，那么他才真正学会了思考.

问题的设置要符合学生的认知水平，要有针对性、递进性、开放性和挑战性，让学生的心灵产生共鸣，理解问题的本质.教会学生思考，其实就是学会用数学的眼光观察问题、用数学的思维思考问题、用数学的方式表达问题，是否学会思考是检验核心素养是否有效的方式，因此，教会学生思考比纯粹教给学生方法更重要.

总而言之，教会学生思考，教师要为学生创设适宜学生的教学情境，让学生用联系的观点、比较的方法深度思考，提升学生的思维力，实现高效和精准教学，从而真正将核心素养落到实处.