基于数学本质的“数系的扩充和复数的概念”教学探索*

●

(绍兴市高级中学，浙江 绍兴 31200)

●徐元根 唐恒钧

(浙江师范大学教师教育学院，浙江 金华 321004)

数学核心素养的培养需要关注数学的本质，既要使学生习得数学知识，更要让学生经历数学研究的过程，体验隐藏在背后的数学思想方法以及研究方法.数学与科学相比，一个独特的特点在于：数学不仅强调实践真理性，还强调逻辑真理性.后者是指从某种程度而言，数学是建立在得到明确定义的数学概念基础上的逻辑体系.在教学中如何让学生体验到该特点，让学生对该特点能有所体会？“数系的扩充和复数的概念”是学生体验上述特点的一个很好的载体，笔者对此案例进行了探索如下：

1 教学案例呈现

1.1 引入悬疑

问题1已知三次方程x3=15x+4，请猜一下此方程的根，并思考如何运算.

设计意图学生在答题时曾多次碰到三次方程，由于三次方程的求根公式在高中阶段不作要求，因此学生面对三次方程多有无从下手的体验.这一问题能激起学生的求知欲望、好奇心.

先让学生猜，有学生猜出其中一个根是4.

师：你是怎么得出来的？

生1：因式分解得(x-4)(x2+4x+1)=0.

师(追问)：这里很巧，能容易地进行因式分解.如果不容易因式分解，怎么办？

在此进一步引入数学史：三次方程的代数解法，数学家已经研究出来了.大约在1535年，意大利数学家塔尔塔利亚宣布发现了三次方程的代数解法，并在多次解三次方程比赛中获胜.意大利的另外一位数学家兼医生卡丹从塔尔塔利亚那里获得解三次方程的诀窍并发誓保守秘密.1545年，卡丹在他的《重要的艺术》里发表了形如x3=px+q的三次方程的解法和其中一个根的表达式[1].那他是怎么解的呢？最重要、最本质的一步是换元，令x=y+z.

紧接着，教师与学生一起解答换元之后的运算过程：已知x3=15x+4，令x=y+z，则

(y+z)3=15(y+z)+4，

从而

y3+z3+(3yz-15)(y+z)=4.

令y3+z3=4，y3z3=125，则y3,z3是t2-4t+125=0的两个根,得

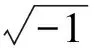
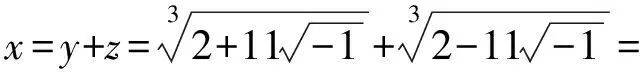
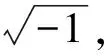
设计意图引入数学史，引入卡丹公式，说明历史上数学家多次碰到负数开平方这个绕不开的问题，也表明这个问题有研究的需要，进而驱使学生寻求解决这个问题的办法.

下面我们来看一下卡丹公式(三次方程其中一个根的表达式)：

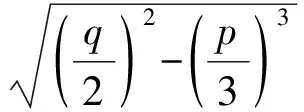
回顾刚才的求解过程可以发现一个普遍现象：实系数方程→运算中出现非实数→暂时搁置这个非实数，继续按实数运算法则进行运算→结果还是实数.

1.2 回顾历史

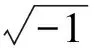
设计意图在回顾过程中，引导学生一起思考：每次扩充引入了什么数？解决了什么实际问题、数学问题？它们有什么共同的特点？也就是要明确扩充的目的和原则，体会到数学发展与数学内部的需要(特别是现实需要)的重要联系.

从自然数集出发，有6种运算：加→乘→乘方;减→除→开方.

问题4对于自然数集而言，负整数是个新数，整数集是个新的数集；对于整数集而言，分数是个新数，有理数集是个新数集；对于有理数集而言，无理数是个新数，实数集是个新数集.那么一个新数集出现，我们要从哪些角度去研究呢？

设计意图引导学生发现学习新数集的一个基本框架，即包括意义的理解、表示及运算这3个方面，这有利于学生有方向、有脉络地去思考，有利于学生对数系发展的整体把握.可通过表1比较扩充前后的运算情况和包含关系.

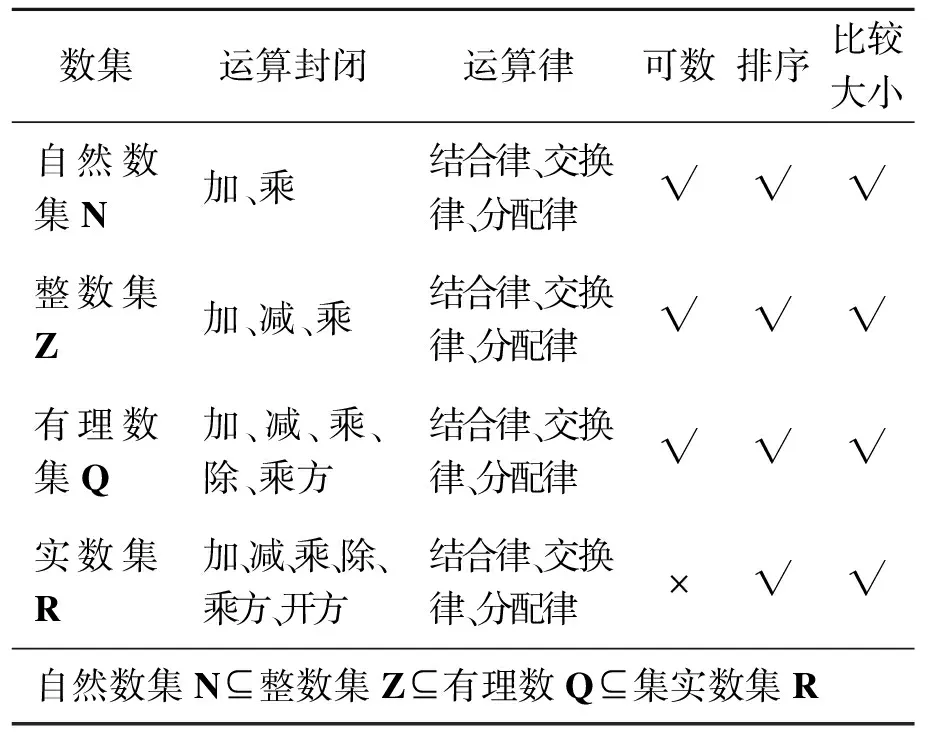
表1 不同数集的特点

1.3 建构新知

问题5大家再来看这个式子

设计意图学生已经亲身体验了一个实数可以表示成带有负数的开平方的形式组合，不得不思考以下问题：负数的平方根具有什么性质？在实数范围内，这些曾经被认为没有意义的根式到底存在怎样的联系？由此解除学生为什么要学习新知识的心理障碍，理解必须引入新数使得负数能进行开方运算以探讨它们的性质.

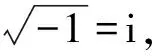
设计意图通过问题解决，引导学生类比，从特殊到一般，归纳概括得出“新数”的一般符号表示a+bi(其中a,b∈R),从而建构复数的相关概念.

问题7i与实数2进行四则运算时，出现了6个式子.你能用一个一般的式子来表示吗？

问题8mi(其中m∈R)是否为a+bi的特殊情况？

1.4 生成理论

给出复数的概念：形如a+bi(其中a,b∈R)的数叫做复数，其中i叫做虚数单位，a叫实部，b叫虚部.全体复数所组成的集合C={z|z=a+bi(其中a,b∈R)}叫复数集.

图1

问题9形如a+bi(其中a,b∈R)的数叫做复数，请问复数a+bi(其中a,b∈R)一定是虚数吗？若不是，何时是实数？何时是虚数？

复数的分类(如图1)：

1.5 例题讲解，深化理解

例1已知复数z=(m+1)+(m-1)i(其中m∈R)，在下列情况下分别求出实数m的值：

1)实数;2)虚数;3)纯虚数.

设计意图让学生在例题的解题过程中内化复数的有关概念，使学生感觉复数的概念没那么抽象，进而对复数概念更加深入理解.

1.6 小结：复数的神奇之处

尽管学生学了复数以后仍然觉得虚数“缥缈而无用”，难以感受复数的应用价值.其实复数是很有用的，它在力学、电力学、热力学、流体力学、量子力学中发挥着巨大的作用，尤其是在建立巨大水电站(如长江三峡水电站)中发挥重要作用.

2 教学反思

2.1 在数学教育中充分重视数学史的利用

数学史是数学概念、思想、方法的起源与发展的历史，也是数学家们用生命和热情追求真理的史诗，可以洞见人类的智慧，也可激发学生的智慧.在数学课堂教学中，应结合所学内容，适时、适度、适量地运用一些数学史料，揭示数学发展的曲折过程，培养学生的探索精神，考查历史上的数学思想方法，强化数学的素质教育.数学史还是一种学习资源，可以激发学生的学习热情.数学史中的问题、疑难、谬误和悖论，这些对于学生的学习而言是很有价值的，能让学生感受到数学学习的必要性，从而激发学习者内在的学习兴趣，使他们乐于其中.

卡丹公式“不可能”情形以及三次方程实根之间的矛盾是16—17世纪数学家们感到困惑的问题之一，这个问题也是本节课学生学习的困惑，是知识的爆发点、生长点.庞加莱指出：教育工作者的任务就是让孩子的思维经历其祖先之所经历，迅速通过某些阶段而不跳过任何阶段[2].波利亚在《数学的发现》中也指出：只有理解人类如何获得某些事实或概念的知识，我们才能对人类的孩子应该如何获得这样的知识，作出更好的判断[3].数学史就有这样的作用，它对人类获取知识的来龙去脉有着清晰的记载，对学生思维的成长有着非凡的意义.教师可以通过思考、整理并将它再现于课堂，不仅能活跃课堂，还能发挥蕴含于数学知识内的深刻的教育价值.

2.2 使用思维框架使学生有脉络地思考

本节课背后的数学思想与自然数集到实数集的扩充有高度的相似性.波利亚曾说过：当遇到两个相似的问题时便可从中总结一套关于它的解题方法，经过不断验证加强或弱化它的效用.于是笔者思考能否建构一种思维框架，是从学生的思维角度出发思考数系扩充的.具体表现在两个方面：一是回顾自然数集到实数集的学习经历，发现数系的扩充都与运算的逆运算有关,引导学生思考运算的不断丰富与数系不断拓展之间的内在关系.二是总结新数集的研究角度，从新数集的意义、表示和运算这3个方面去研究，进而引导出表1的内容.

教师注重相似知识点的结构化处理有助于学生有脉络地思考，从而为学生的自主学习、自主研究提供载体，真正提高学生的数学思考能力，也有助于学生对知识进行结构化记忆.

2.3 经历数系扩展过程推动学生数学素养的提升

数学核心素养具有6个数学基本特征：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析，这些是在数学学习的过程中逐步形成的.本课中，学生困惑的是卡丹公式中的“不可能”情形及其运算过程和三次方程实根之间的矛盾现象，即在实数运算中出现了不是实数的“数”，而结果却仍然是实数.换言之，这里出现了数学上的逻辑漏洞.面对数学的逻辑漏洞，历史上又是如何处理的呢？初中数学中为了弥补一些有理数的开平方数不是有理数，而引进了无理数，从而使数系扩充到实数.现在出现了负数的开平方数，它不是实数，但这个数又确实存在.为了弥补这个逻辑漏洞，只能将数系再次扩充，进而变成复数系.在这个学习过程中，一方面漏洞的发现依靠逻辑，这对于学生逻辑推理素养的发展作用是明显的；而另一方面，漏洞的弥补过程其实是一个数学模型的建立过程，而数系扩充以及新数学习的过程又充满着逻辑推理与数学运算素养的培养.因此，让学生去经历数系扩充的过程，有助于学生多种素养的提升.

总之，本节课试图通过历史还原、有脉络的思维以及过程经历使学生的数学学习更具数学本质.当然这仅仅是一个初步的尝试，还有待进一步的深入研究.