何以致疑 疑归何处*——探析数学教学的课后答疑

●

(义乌中学，浙江 义乌 322000)

在数学学习中，数学教学内容的逻辑性、抽象性以及学生个体差异的客观存在使得学生会产生各种各样的困惑[1]，这就需要教师在课后进行适当地答疑解惑．课后答疑作为数学教学的一个重要环节，是课堂教学的有效补充，是教师了解学生思维方式以及对知识掌握程度的重要途径，是提高教学效果的有效手段[2]．本文就数学教学的课后答疑谈几点思考．

1 答疑目标

很多人认为答疑的目的就是“不疑”，就是解决问题，因此在答疑过程中往往会就题论题、直接告诉学生答案，甚至不厌其烦地给学生提供详细的解答过程．学生可能当时已经理解，但换一个背景后是否能顺利解出却不得而知．随着教学经验的积累，笔者认识到“不疑”仅仅是一个比较浅层的目标，它更深层次的目标是“通达”，也就是使学生能触类旁通、举一反三、解决一系列同类的问题．再后来觉得通达也不是答疑的最终目标，那是什么呢？法国数学家劳厄尔认为教育的真谛是“所有学会的东西都忘却了以后仍然留下来的那些东西”，也正如日本著名数学教育家米山国藏说的“作为知识的数学，(学生)出校门不到两年就忘了，惟有深深铭记在头脑中的是数学精神、数学思想、研究方法和着眼点等，这些却随时随地发生作用，使他们终生受益”．学生在答疑解惑过程中从会到不会的体验，学会数学地思考，在思考中不断提升思维能力，这或许就是答疑的价值所在．

2 答疑现状

数学教学的课后答疑现状究竟如何呢？以下几个“=”成立吗？

2.1 答疑=鼓励？

教师首先应对会提问的学生加以肯定和鼓励，但同时也要加以辨别和区分，不能“一视同仁”．有些学生的目的指向很明确，认为自己的解答很有理，但不知错在哪，这类学生应该予以大力表扬，精心呵护他们的求异和不盲从精神；对于那些胆小和对数学有畏惧心理的学生，教师要先消除其胆怯和紧张的情绪，鼓励学生多说说对所提问题的理解和想法；对于那些没有经过任何思考直接拿了题目来问的“懒汉”，教师则应当批评．

2.2 答疑=告知？

我们知道“直接给出答案”和“一讲到底”对学生的帮助都不是很大，但我们也不能一概否定传授型的答疑，这种方式对于数学基础比较差和容易紧张的学生还是比较有效的．教师在给学生分析和解答的同时，要引导学生适当地参与，以防教师越位变成答疑的主体．

2.3 答疑=点拨？

“答疑不答，贵在启发”这个观点受到普遍的肯定．在学生的困顿之处从知识或方法上给予一定的点拨[3]，让学生从“山穷水复疑无路”的困惑中感受到“柳暗花明又一村”的惊喜．但学生很大程度上欠缺的就是如何想到教师“点拨”的那个关键点或难点．教师在“点拨”中经常会不自觉地给学生铺设一个又一个的台阶，“一步一搀扶”，点拨中带有一定的暗示和指向性，以让学生最终达到成功的彼岸，其实这种点拨某种意义上来说也是一种变相的包办，这就需要教师在答疑中把握好点拨的尺度．

3 答疑动因

答疑如同医生看病，教师首先要明白疾病的症结在何处，即“疑到底从何处来”.造成学生疑惑的原因可能是知识本身比较抽象难以理解，也可能是教师在教学过程中节奏比较快、思维跳跃过大，但最主要的还是学生自身的因素．教师可以从学生的心理(情感)、认知和能力这3个方面进行分析[4]．

3.1 心理分析

心理素质是影响学生学习的重要非智力因素．有些学生对数学有莫名的恐惧心理，学习中的畏难情绪阻碍了他去积极地思考，看到稍微复杂一点的题目就不敢动笔尝试．也有的学生表面上很好问，不懂就问，但实际上是懒于思考，缺乏主动性，看到稍微难一点的题目就不想做．这就要求教师设法激发学生思考的积极性，让学生主动参与答疑过程以寻找解决疑问的“突破口”，让学生自己解决问题，而不是被动地等待教师给出答案．

3.2 认知分析

布鲁纳的认知发展理论认为：学生学习的过程实际上是利用已有的认知结构对新的知识经验进行加工改造并形成新的认知结构的过程．新旧知识在学生头脑中相互作用会使原有知识结构不断分化和重新组合．而每个学生的原有认知水平不同，对概念的理解、公式定理的掌握程度不一，因此教师在答疑时应该摸清：学生的基础是什么,已经知道了哪些基础知识,掌握了哪些基础方法,是否已经建构了知识网络.

例1已知两条直线l1：(m+3)x+4y=5-3m，l2：2x+(5+m)y=8相交，则m的取值范围是

( )

A．m≠-1 B．m≠-7

C．m≠-1或m≠-7 D．m≠-1且m≠-7

该题考查的是两条直线在斜截式和一般式形式下位置关系的充要条件．开始的估计是：1)学生可能会在“且”“或”和取舍上产生疑问；2)考虑到来问的学生基础很薄弱，估计他想不到一般式情形下的充要条件，用的应该是斜截式．在实际的交流过程中验证了笔者估计的情形2)是正确的，学生用了斜截式，但不知道k1,k2是什么，不知道将已知直线方程改写成斜截式，在估计他可能“摔倒”的地方之前他早已经“倒下”了．

因此，教师在答疑时应该充分考虑到学生原有的认知结构和知识储备情况，不能凭经验想当然地认定学生解题时出现的认知障碍是什么．

3.3 能力分析

不同的学生对新知识的接受能力、新旧知识的整合能力、系统归纳能力、对问题的分析探究能力、对知识的迁移能力、在解答过程中的运算能力以及思维的严密性上都存在差异．因此答疑时必须从学生实际出发，针对不同学生的思维缺陷给予不同的引导，注重思维能力与方法的培养[5]．

4 答疑策略

答疑的主体是学生，教师只是起到一个辅助的作用，在答疑时要“想学生所想、想学生所难、想学生所惑”，但不能包办代替，也不能主观臆断，而应从学生实际出发，有的放矢地进行．对于课后答疑，我们可以作以下尝试．

4.1 学生为先，把脉为要

答疑的主体是学生，只有自己对题目有一定的思考，答疑才会有效．因此，答疑时宜让学生先说或者拿着尝试解答的草稿来问，通过学生的先说(写)让教师更好地把脉症结所在，是审题原因还是知识、方法上的缺失，从而让答疑中师生的思路和方法走得更加融洽自然，更贴合学生已有的认知，更贴近学生的最近发展区．

4.2 角色转换，以问代答

师生可以进行角色转换，由学生问教师答变为教师问学生答，学生可从回答教师问题的过程中，弄清相关基础知识，排除造成疑难的各种障碍，最终找到正确答案并感悟思考问题的方法．

4.3 化大为小，化难为易

对于条件较多的题目，教师可以鼓励学生进行“挖坑”行动，和学生一起对已知条件逐一分析，从“已有什么”“能得什么”“要求什么”“还要什么”等方面思考如何将已知和未知联系起来．对于有些大题目可将其分解成若干个小题目，以降低难度，便于学生入手并步步推进．如高一时“函数”一章学完后有学生来问这样一道题目：

师：你能从题目中得到哪些信息？

生1：1)奇函数；2)f(x+1)=f(x-1)；3)当0≤x≤1时的函数解析式．

师：你能从这些信息中得到什么吗？

生2：由奇函数可知f(-x)=-f(x)或者图像关于原点对称，但不知道用哪个，条件2)不知怎么用，条件3)也没法用．

师：那我们来看看要求什么？

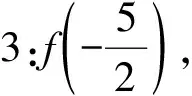
师：那你能根据已知条件把自变量转换到[0，1]内吗?

学生在“挖坑”中不知不觉地把问题解决了，他意识到看着让人头大的题目实际上也没那么难，而且是自己分析得到结果的，觉得很有成就感．

4.4 答非所问，化生为熟

对于数学能力比较好的学生，教师可先引导学生去解决另外一个与本题类似或有关联的较简单、较熟悉并容易理解的题目，让学生在解决其他题目的过程中得到启迪，达到自己悟懂的目的，从而发展学生的知识沟通能力和知识迁移能力．

4.5 师生互动，生生互动

答疑过程可以师生双向，也可以教师和几个学生多向进行，相互启发、相互学习，在讨论中发散各种思路，教师也能从讨论互动中了解学生的想法和困惑，发现学生的解题灵感，碰撞出思维火花，同时还可以发现自身教学中有待改进的地方．

4.6 量体裁衣，因材施教

不同的钥匙开不同的门，即使讲解相同的题目，对于不同的学生，答疑的方式和交流过程中的方法也应有所不同，让不同层次的学生都有所收获．对于学有余力的学生，教师可点到即止，也可采用“一题多解”“多题归一”等方式进行适当地扩展延伸，对同种类型、同种数学思想方法的问题进行整合，“由此及彼、由表及里”，让学生有“千变万化、不离其宗(本质)”的感觉．而对于学习相对困难的学生，他们需要教师更多的耐心和细致．教师可引导学生学会联想、在掌握通解通法的基础上再适当掌握一些技巧，也可通过“一题多变”使基础知识和基本方法得到巩固和提高．

教之道在于度，学之道在于悟，“道而弗牵，强而弗抑，开而弗达”，只有师生“双轮驱动”，相向而行，才能解心中之惑，释心中之疑，由懂到会，由会达熟，由熟生巧．