在深度对话中提升交流与反思能力*
——以一道高考压轴题的探究为例
2019-03-06
●
(闽清教师进修学校,福建 闽清 350800)
“交流与反思”是数学核心素养的主要体现之一,其主要是指“能够用数学语言直观地解释和交流数学的概念、结论、应用和思想方法,并能进行评价、总结与拓广”[1].对话是交流与反思的主要途径.数学教学是一场深度对话,是师生、生生间的语言对话,也是师生与数学文本的对话,还是师生教学反思的自我对话,更是师生与数学本质的对话.通过深度对话让学生在“对话”中经历数学概念和结论的形成与发展过程,提升交流与反思能力,发展数学核心素养.本文以一道高考压轴题的探究为例,阐述数学对话教学的体会.
1 标解疑惑
笔者课前把2018年浙江省数学高考压轴题及命题组给出的参考答案印发给学生,要求学生与参考答案对话,思考命题组的思路是怎样形成的,是否还有不同的思路.

1)若f(x)在x=x1,x=x2(其中x1≠x2)处导数相等,证明:f(x1)+f(x2)>8-8ln 2.
2)若a≤3-4ln 2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
(2018年浙江省数学高考试题第22题)
命题组给出的第2)小题的参考答案为:

f(m)-km-a>|a|+k-k-a≥0,
于是存在x0∈(m,n)使f(x0)=kx0+a.因此,对于任意的a∈R及k∈(0,+∞),直线y=kx+a与曲线y=f(x)有公共点……
对话体会数学文本一般只呈现逻辑结论,省略了数学概念、结论、应用的形成发展过程.因此要求师生与文本进行对话,从本质上把握文本意义.在与文本对话时要努力挖掘被省略的知识发生、发展过程,把数学文本的学术形态转化为教育形态.
2 问题探究
f(m)-km-a>0,f(n)-kn-a<0,
让人如坠烟海,百思不得其解.
生1:直线y=kx+a与曲线y=f(x)公共点个数等价于方程f(x)=kx+a实根的个数.设
等价于函数g(x)零点的个数.对k>0,当x→0+时,g(x)→+∞,当x→+∞时,g(x)→-∞,由图像知,连续函数g(x)在(0,+∞)上至少存在一个零点.
师:直观想象有助于思维,但不能替代逻辑推理.
生2:根据零点存在定理,要找到正数m,n使g(m)>0,g(n)<0.根据以往经验,取特殊函数值
g(1)=1-k-a,
但都不能确定其符号.
生3:g(x)中含有k,a,所找正数m,n应该也含有k,a,但具体是什么很难知道.
(学生苦思冥想,找不到突破的方向,求助的目光投向教师.)
师:以前所找的特殊函数值能确定符号可能是巧合或函数比较简单.能否把g(x)化归为简单的函数,即把g(x)放缩为简单的函数h(x),使g(x)>h(x)(或g(x) h(m)≥0(或h(n)≤0), 则 g(m)>0(或g(n)<0). -(1+k)x+1-a. (全班为生4鼓掌.) 师:生4利用重要不等式lnx≤x-1把超越函数g(x)放缩为一次函数后找到m.还可怎么找? 则 当x∈(4,+∞)时,t′(x)>0,t(x)单调递增;当x∈(0,4)时,t′(x)<0,t(x)单调递减,故 t(x)≥t(4)=2-2ln 2, 令2-2ln 2-kx-a=0,解得 生6:当x>0时,由k>0得-kx<0,方向不对,无法缩小. 师:是啊方向不对,希望得到-kx>____的不等式. 生6:当x>0时,得不到-kx>____的不等式. 师:对,除非对x设定范围,怎么设定? 生6:-kx>____,即x<____,最简单就是设0 令-lnx-k-a=0,解得 x= e-(k+a), 于是取m= e-(k+a)时,g(m)>0. 生7:似乎不妥.当0 生8:取m= e-(k+|a|),满足0 师:是从参考答案中看到的还是自己想到的? 生8:修改一下生6的解法就可以了!当0 -lnx-k-|a|, 令-lnx-k-|a|=0,解得x= e-(k+|a|),于是取m= e-(k+|a|)时,g(m)>0. (教室里掌声雷动.) 师:太棒了,你们还原了命题专家的心路历程,可以参加高考命题了! 对话体会在问题探究时,教师使用启发性话题,即引导学生一步步走向问题解决的铺垫性话题.话题紧贴学生思维最近发展区,在学生思维顿塞处引导学生不断地运用已有的知识经验,通过一系列循序渐进的感知、体验和探究,促进数学知识的建构和数学结论的发现. 学生的对话,教师要予以评价.当学生回答不出问题时,教师要予以救场,给学生提供支持和帮助,呵护学生的自尊心;当学生理解错误时,教师要予以归因,让学生剖析问题的症结;当学生观点可取时,教师要予以采纳,保护学生对话的积极性;当学生取得成果时,教师要予以赞赏,促使学生进入情绪高昂和智力振奋的学习状态. 师:再寻找n. 生9:要寻找n使g(n)<0,需把g(x)放大为简单的函数,为消去lnx,根据生6、生8的经验,设x>1,则 师:生11把g(x)放大为h(x),再通过解不等式h(x)≤0寻找n,这种做法更具一般性. 生12:当x>1时, 生13:当x>1时,kx>k,lnx>0,从而 当x>1时,也不能保证不等式(1-k)x-a≤0有解. 生(众):山穷水尽疑无路. 师:当x>1时,影响(1-k)x-a≤0有解的因素有哪些? 生15:x项系数含有字母k…… 师:能否使x项系数不含k? 生16:提取k,当x>1时, 生17:提取x,当x>1时, 做不下去了. (全体学生激情绽放.) 对话体会问题是思维的源泉,是对话的焦点.对难度较大的问题,学生往往思路茫然、解题错误、答非所问、理解偏差,这些让教学一波三折的跌跌撞撞真实地反映了学生知识、方法上存在的问题,袒露了学生的思维现状,使教师能即时掌握学情,极具教学价值.对学生的跌跌撞撞,教师不能置之不理,也不要急于纠正学生的错误,更不能直接抛出预设的方法.教师要因势利导,引发师生、生生间的深度对话,在对话中互相修正、互相补充、互相借鉴、互相启发,从而激发学生的元认知活动. 师:我欣慰地感到同学们的逻辑推理、数学运算、直观想象、数学抽象素养在提升.现在反思本课的学习,总结探求函数零点存在区间的策略. 学生踊跃发言,教师补充整理: 探求函数零点存在区间,即在零点两侧探求实数m,n(可以是一个具体的数、式或区间),使f(n)f(m)<0. 1)特值验证:根据函数式的特征,取特殊自变量m,验证是否满足f(m)>0(或f(m)<0); 2)解不等式:当不等式f(x)>0(或f(x)<0)可解时,可直接通过解不等式求出满足f(m)>0(或f(m)<0)的实数m; 3)放缩化归:当f(x)较复杂时,可将f(x)放缩为简单的函数g(x),使f(x)>g(x)(或f(x) 为便于放缩,可根据函数图像和解析式特征在某限定范围内进行放缩.对含有指数、对数函数的要注意运用重要不等式ex≥x+1,lnx≤x-1进行放缩. 对话体会教师使用反思性话题,让学生反思学习过程,在自我对话的基础上师生总结出解决问题的通法通则,彰显自我人性,把握数学本质. 师(下课铃声响了):试题是否有几何背景?试题能否拓展?请同学们课后思考,下课! 对话体会为给学优生创设思维驰骋的空间,教师在课末使用拓展性话题,要求学生进一步提出可拓展延伸的问题.本试题的几何背景是当直线y=kx+a为过y=f(x)图像拐点(16,4-4ln 2)的切线时,a=3-4ln 2.由图形知当a≤3-4ln 2时,对任意k>0,直线y=kx+a与y=f(x)有唯一公共点. 巴西学者弗莱雷认为:没有了对话,就没有了交流;没有了交流,也就没有真正意义的教育[2].在新一轮课程改革中,教师要以“对话教学”为抓手,提升学生交流与反思的能力.通过深度对话,在思维建构中把握本质,形成素养;在交流中取长补短,互惠共赢;在反思中内化醒悟,加深理解;在评价中树立信心,体验喜悦;在总结中揭示规律,提炼通法;在拓展中深化思维,提出命题.
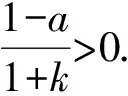


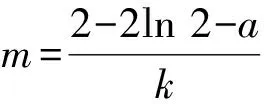

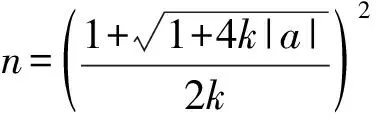
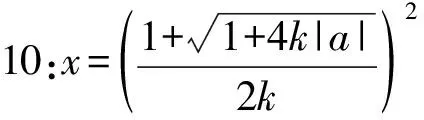




3 结束语
