基于自适应拟合建模的航空发动机健康参数估计*
2019-03-05顾嘉辉黄金泉强子健
顾嘉辉, 鲁 峰, 黄金泉, 强子健
(南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室,江苏 南京 210016)
0 引 言
航空发动机长期在高温、高压和高转速的恶劣环境中工作,会发生缓慢的性能退化现象,影响飞行安全[1,2]。通过收集商用航空发动机的机载传感器数据可以对发动机的状态进行监视与故障诊断[3~5],分析性能退化的程度帮助制定维修策略,从而提高飞行安全和降低航班延误率。
航空发动机的气路健康状态常用各个部件的流量和效率的相对变化量(即健康参数)来表示,然而由于其无法直接测量,只能根据机载传感器的测量值,如两个转子转速和各个截面的压力和温度通过算法进行估计。常用的方法有各种滤波算法[5~8]。
在状态估计方面,卡尔曼滤波算法研究得较多[6~10],然而发动机部件级模型计算量较大,使得非线性滤波算法目前难以满足机载实时性要求,同时发动机线性状态变量模型(state variable model,SVM)存在建模误差,使得线性卡尔曼滤波算法对健康参数的估计精度较低。
常用的发动机状态变量模型建模方法有:扰动法[11]、拟合法[12]、改进拟合法[13]等。但系数矩阵仅通过对发动机模型在某些特定的性能退化下扰动或拟合得到,对于这些特定情况以外的性能退化情况,由于发动机非线性特性强,线性模型精度较低,因此健康参数的估计误差会随着飞行循环数的增加,逐渐变大。本文提出自适应拟合法来建立含健康参数的状态变量模型。该方法利用上一个采样周期内健康参数的估计值实时重新计算健康参数相关系数矩阵,以提高线性模型在各种退化程度下的精度,从而使得加载了卡尔曼滤波器的状态变量模型能够在全寿命期限内较准确地估计健康参数。
1 基于自适应拟合法建模的航空发动机状态变量模型
1.1 航空发动机非线性模型
本文使用的航空发动机非线性模型为某型大涵道比涡扇发动机部件级模型[14],共有5个旋转部件:风扇(fan)、低压压气机(low-pressure compressor,LPC)、高压压气机(high-pressure compressor,HPC)、高压涡轮(high-pressure turbine,HPT)和低压涡轮(low-pressure turbine,LPT)。
假设该发动机部件级模型可以表示为

(1)
式中 状态量x=[N1N2]T为风扇转速与高压转速,输入量u=[WfVSV]T为燃烧室燃油流量与高压压气机导叶角度,飞行条件v=[HMa]T为飞行高度和飞行马赫数,输出量y=[N1N2T25P25T3P3T495P13]T为两转子转速、低压压气机出口总温和总压、高压压气机出口总温和总压、排气温度以及外涵道出口总压。
1.2 航空发动机状态变量模型
在发动机某稳态点(x0,u0,v0)附近对式(1)进行泰勒级数展开,忽略二阶及以上分量,就可以得到发动机在该稳态点附近的小偏差线性状态变量模型
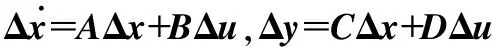
(2)
式中Δx为发动机状态量的增量,Δu为输入量的增量,Δy为发动机输出量的增量,A,B,C,D为相应维数的系数矩阵。考虑航空发动机在服役一段时间后,其气路部件性能会不可避免地发生退化,从而导致发动机工作状态偏离其额定状态。因此在状态变量模型中增加了能够表示发动机部件性能退化程度的健康参数,描述真实发动机动态特性的状态变量模型应为
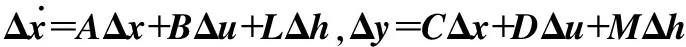
(3)
参照文献[15]给出的某型航空发动机的每个健康参数在不同飞行循环数下的大小可知,在飞行循环数6 000后,低压涡轮流量和效率的变化依然非常小,绝对值都在1 %左右。同时,考虑到卡尔曼滤波算法中状态量的可观性要求,式(3)中,Δh为不包含低压涡轮流量和效率的8个健康参数组成的列向量
Δh=[SW1SE1SW2SE2SW3SE3SW4SE4]T
(4)
式中SW,SE分别为对应流量和效率健康参数、下标1~4分别对应风扇、低压压气机、高压压气机和高压涡轮。式(3)中Δu和Δh对于状态变量模型的作用相同,在建模时都可以作为控制量来考虑,因此式(3)可以改写成

(5)
1.3 自适应拟合建模法
自适应拟合法首先参考文献[5]发动机参数性能退化的范围对每个旋转部件健康参数的可能变化范围进行划分,如表1。

表1 各部件健康参数划分范围 %
可知,在进行健康参数估计前:不考虑低压涡轮流量和效率健康参数,则可能出现的气路健康参数的组合有4×4×5×4=320种。将所有可能的健康参数组合记为
Δh(i)=[SW1(i)SE1(i)SW2(i)SE2(i)SW3(i)SE3(i)SW4(i)SE4(i)],i=1,2,…,320
(6)
将320组健康参数组合注入部件级模型中得到由于性能退化引起的稳态状态偏差和输出偏差,分别记为
(7)
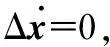
(8)
在开始健康参数估计前,将输出偏差,即8×320数组和所有系数矩阵都以单浮点精度(MATLAB中为Single)形式保存在mat.文件下。
机载进行健康参数估计时,根据前一时刻健康参数的估计值从mat.文件中选择最接近的、线性无关的8组健康参数组合Δh(si),i=1,2,…,8(行向量)以及对应的Δy(si),Δx(si),i=1,2,…,8(列向量),利用于更新L,M矩阵:对i=1且不考虑控制量,当系统稳定后有
(9)
类似的方程组共有8组,对应选中的8组健康参数组合。将8组方程组进行整理,对式(9)的第一式有


(10)
式中 ΔH1(si)为2×16维矩阵,L(j,:)为L矩阵第j行所有元素组成的行向量,0为1×8维零矩阵。该式中未知量仅为L(1,:),L(2,:),即L矩阵可解。对式(9)的第二式有

(11)
式中 ΔH2(si)为6×48维的矩阵,M(j,:)为M矩阵的第j行所有元素组成的行向量,0为1×8维的零矩阵,()3:8为该列向量的第3到第8行。同理,M矩阵可解。将该时刻计算得到的L,M矩阵代替式(8)中原来的L,M矩阵,再进行健康参数估计,然后下一时刻重复该步骤。
关于线性无关样本的选择方法,按各部件健康参数组合的欧氏距离进行排序,以风扇部件为例说明如下:假设前一时刻风扇流量和效率健康参数的估计值为:S1=-3.5 %,S1=-3.4 %,对应图1中菱形所示,图中另外4个离散图形对应表1中风扇健康参数的4组样本。

图1 风扇健康参数样本分布
计算4组样本与当前估计值对应的风扇健康参数的欧氏距离的平方r1(i)(下标1~4分别对应风扇、低压压气机、高压压气机和高压涡轮,下同)
r1(i)=(S1-SW1(i))2+(S1-SE1(i))2
(12)
将r1(i)(i=1,2,3,4)中最小距离平方对应的样本序号(即表1中的序号)记为q1。类似得到q2~q4,则8组线性无关样本的各部件健康参数对应的序号可以选取为

(13)
相比改进拟合法,自适应拟合法不再更新式(8)中的A,B,C,D,Kst矩阵,仅由前一时刻健康参数的估计值从mat.文件中选取8组健康参数组合,按照式(10)、式(11)简单计算L,M矩阵,以此提高线性状态变量模型在各种性能退化情况下的模型精度,使得结合了线性卡尔曼滤波器的该线性模型能够在全寿命期限内准确估计健康参数。
2 设计点数字仿真验证
2.1 性能缓慢退化的仿真验证
本文在设计飞行点(H=10 668 m,Ma=0.785)从慢车以上(N1=70 %)到最大状态(N1=110 %)采用自适应参数拟合法建立13组离散的系数矩阵Aa,Ba,Ca,Da,Kst与320种输出偏差Δy(i)组成的高维数组,对于该飞行点的其他状态以风扇换算转速为索引,采用线性插值的方法获得系数矩阵与高维数组。
数字仿真时分别采用改进拟合法与自适应拟合法建模,使用线性卡尔曼滤波器对健康参数进行估计,以验证自适应拟合法建模的有效性和精度。对于改进拟合法建模时各健康参数的阶跃量统一选取绝对值大小为5 %。数字仿真时间为60 s,采样周期为25 ms(即2 400个采样周期),性能退化从第二个采样周期开始线性缓慢变化,到第60 s时退化到对应6 000飞行循环数[5]。此外,虽然状态变量模型中没有包含低压涡轮的流量和效率健康参数,但数字仿真中依然参考文献[5]参数退化表中飞行循环数6 000参数退化情况,加入了低压涡轮的性能退化。同时假设输出传感器含高斯白噪声,满足vk~N(0,Rk),其中Rk=0.0022I8×8,以及加入PID控制器对风扇物理转速闭环控制[17]。本文的所有数字仿真都是在个人笔记本电脑Windows 10系统的32位MATLAB R2012a下完成,其配置为:i5—6300HQ @ 2.30 GHz,4 GB RAM。
图2分别为两种建模方法在设计飞行点的巡航状态 下模拟性能缓慢退化的健康参数估计结果。

图2 2种建模方法下健康参数的估计结果
由图可知,基于改进拟合法建模的LKF随着飞行循环数的增加,健康参数的估计误差逐渐加大,主要原因是改进拟合法只能在建模时选取的健康参数阶跃量附近的小范围内模型误差较小,其他退化情况下模型精度都难以保证。相比之下,自适应拟合法建立的线性模型由于实时更新L,M矩阵,模型精度始终保持较高,因此对健康参数的估计误差明显小于前者。
本文健康参数的个数为8个,故改进拟合法建模样本的个数为8,而自适应拟合法由于样本个数的增加,模型精度得到提高,但增加了存储空间、降低了机载实时性。图3为自适应拟合建模法不同样本数下,对文献[5]退化情况表的健康参数估计精度、存储空间和计算时间的关系。图中健康参数的估计精度用均方根误差总和sum(RMSE)表示
(14)

图3 样本个数对估计精度、存储空间和计算时间的影响
图3中存储空间为该设计点下从慢车到最大的离散13组系数矩阵以及对应的健康参数组合引起的输出偏差数组的总大小。此外,参考文献[18],该线性模型还加入BP神经网络(用于补偿由于发动机制造、安装等造成的个体性能差异以及通过相似换算扩展到其他飞行点后带来的稳态偏差),故计算时间为个人笔记本上包含神经网络的线性模型的总运行时间。本文折衷考虑,故选择自适应拟合法建模样本的个数为4×4×5×4=320。
2.2 含气路突变故障的仿真验证
考虑到发动机个体性能退化的差异以及可能出现气路突变故障,参考文献[5]参数退化表模拟另外2种含气路突变故障的性能退化情况,如表2,表中括号内为在性能退化的基础上在3 000飞行循环时注入的气路突变故障的大小,故障参考文献[6],选取Level 1故障,以检验突变故障的诊断能力。
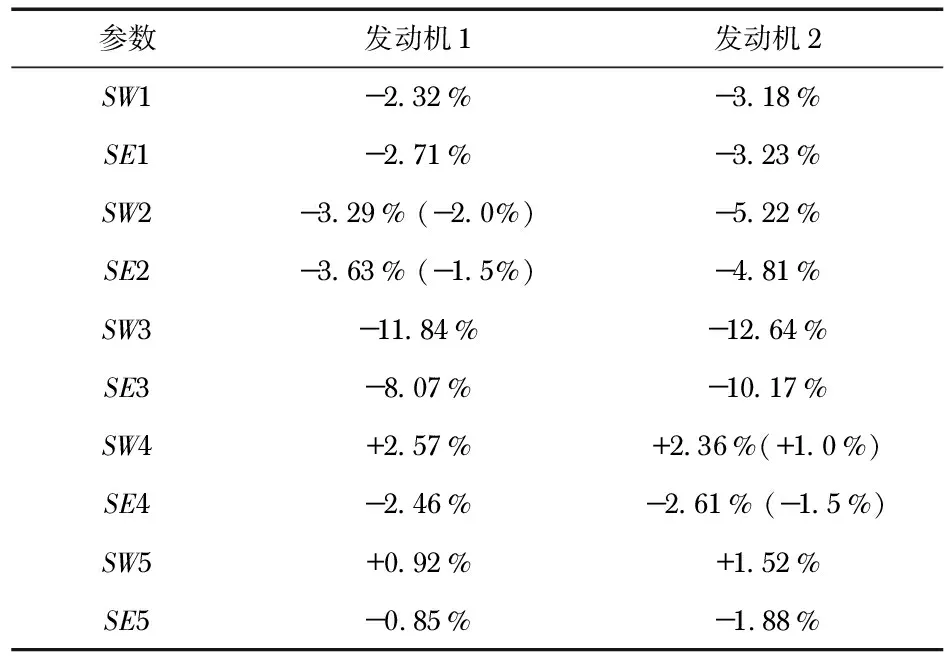
表3 2种发动机健康参数退化情况
自适应拟合建模法对2种退化情况的估计结果见图4(a1)和图4(b1)。针对气路突变故障的诊断,采用一定时间内健康参数的变化量mk作为检测依据
(15)
设定阈值,当|mk|≥0.003时,说明发生气路突变故障,如图4(a2)和图4(b2),此时需要结合健康参数的估计结果进行故障诊断。对于本文,一个飞行架次内只采样一组数据,而真实飞行时,阈值的设置需综合考虑采样周期、传感器特性和卡尔曼增益矩阵大小。

图4 自适应拟合法建模的LKF估计结果
3 飞行区块数字仿真及结果分析
由于真实的航空发动机在每个飞行循环内的巡航状态时,其飞行高度H、飞行马赫数Ma和风扇转速N1都不一定是设计值。因此对于设计飞行点附近的其他飞行状态点先采用相似换算、再按照风扇换算转速插值系数矩阵和输出偏差数组、然后用自适应拟合法重新计算L,M矩阵的方法来估计气路健康参数。为了确定相似原理的适用范围,参考文献[19],计算全飞行包线内各个飞行点距离设计飞行点的广义距离
(16)
式中T2ds与P2ds为设计飞行点的风扇进口总压和总温。设定阈值d≤0.07,得到相似原理的适用范围大致由以下4个飞行点:1)H=9 300 m,Ma=0.60;2)H=11.1 km,Ma=0.90;3)H=9.9 km,Ma=0.60;4)H=11.7 km,Ma=0.90组成的平行四边形飞行区块。
选择该飞行区块的4个顶点,每个飞行点下选取13个不同的风扇换算转速,每个飞行状态都参考文献[5]发动机参数退化表的6 000飞行循环数模拟性能缓慢退化,记录每个飞行状态点的8个健康参数均方根误差总和(sum(RMSE)),得到图5。

图5 2种建模方法下4个飞行点健康参数估计误差总和
可知,在该飞行区块4个顶点的各个风扇换算转速下,采用自适应拟合法建模的线性卡尔曼滤波(linear Kalman filtering,LKF)相比改进拟合法建模的LKF对健康参数的估计误差明显减小,尤其对于N1=95 %以上的状态点,均方根误差总和减小40 %以上。
4 结束语
1)相比改进拟合的建模方法,基于此模型的卡尔曼滤波器对健康参数的估计误差大大减小;
2)仅增加2个矩阵简单计算,故实时性较高,数字仿真时间60 s下计算时间小于20 s;
3)通过采用相似换算,整个飞行区块内从慢车到最大的所有矩阵和数组的存储空间小于200 kB,考虑到该发动机为商用,其巡航包线较小,总存储空间不大于1 MB。
