基于电磁驱动的微扑翼飞行器驱动器振动特性*

张 钰， 刘志伟

(北京航空航天大学 能源与动力工程学院，北京 100191)

0 引 言

微型飞行器是指结构尺寸通常小于15 cm，重量在10～100 g之间的一种新式飞行器，有固定翼、旋翼和扑翼三种飞行方式，当微型飞行器翼展小于7.5 cm时，扑翼飞行是最佳飞行方式[1]。微型扑翼飞行器的机动性、续航时间等重要飞行指标与采用的动力系统密切相关，而其中驱动器是核心部件[2]。随着加工工艺以及设备的发展，相比于传统静电、压电驱动器，电磁驱动器驱动力大、驱动电压低、功耗小的优势越来越明显[3]。基于此，本文提出一种新型电磁驱动器方案，建立电磁场中微梁振动模型，针对模型中三个影响微梁梁端振幅的影响因素，即驱动电压、磁感应强度、电流角频率，设计开展电磁驱动的微梁振动试验，验证电磁驱动器方案的可行性，基于微梁振动模型探究相关因素对微梁振动的影响规律。研究结果为后续微型扑翼飞行器电磁驱动器的优化研究奠定基础。

1 电磁驱动器方案

磁场对其中的运动电荷或者载流导体有力的作用，若给导体施加一定约束，则其在安培力作用下受迫振动，受迫振动频率即为交变电流频率[4,5]，如图1(a)所示。基于此本文设计一种新型微扑翼飞行器电磁驱动器方案，如图1(b)所示，其中记忆合金丝微梁约束于稳定磁场中，通以交流电实现微梁振动拍打，两外伸端安装扑翼翅膀结构用于模拟扑翼飞行。

图1 磁场中载流导体受力与电磁驱动器方案

2 基于电磁驱动的微梁振动模型

本文基于电磁驱动原理，运用连续系统概念，建立磁场中载流简支微梁振动模型，作为开展后续微梁振动试验的基础。连续系统中假设如下：1)材料是均匀各向同性的；2)服从胡克定律；3)满足小变形条件；4)忽略空气阻尼[6,7]。

微梁振动简化如图2所示。

图2 微梁振动简化

其中匀强磁场磁感应强度为B，微梁长为l，截面积为A，密度为ρ，通有交流电I。假设微梁为欧拉—伯努利梁，只考虑弯曲变形，不计剪切及扭转变形的影响,则横向振动的偏微分方程为

(1)

式中q(x,t)为单位长度分布力。

不计阻尼的情况下，假设t=0时，电流I=0，则I=Imsinωt，微梁单位长度上的电磁力为

q(x,t)=BImsinωt

(2)

由于载荷为简谐激励，式(1)的解直接为稳态解。假设方程解的形式为

y(x,t)=ω(x)φ(t)

(3)

式中ω(x)为位移函数，φ(t)为时间函数，令时间函数形式为

φ(t)=sinωt

(4)

联立式(1)～式(4)，得到微梁稳态振动响应为

sinωt

(5)

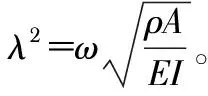
(6)

由式(6)可得，电磁驱动下微梁振幅受到磁感应强度B、交流电最大值Im(即电压最大值Um)、交流电频率ω等外部因素影响。

3 电磁驱动微梁振动特性试验

基于式(6)得出的振动模型，B,Im,ω对微梁振幅的影响规律，为此开展电磁驱动微梁振动特性试验。试验基于记忆合金丝微梁在永磁体磁场中的振动原理，试验装置分别有能量输入装置，振动试验件、振动形态记录测量装置。函数信号发生器提供驱动电压，高速相机采集微梁振动时的变形情况并测量，振动试验件是0.1 mm记忆合金丝微简支梁结构，稳定磁场由两块NdFeB系N35永磁体材料，如图3(a)所示，试验示意如图3(b)所示。微梁梁端微小振幅测量方法如图4所示。通过高速相机拍摄微梁全振幅振动过程，在屏幕上放大量取后，换算至梁端实际振幅。屏幕显示振幅与微梁实际振幅间换算关系为γ=9 mm/3.5 mm=2.571 429。

图3 矩形永磁体与微梁振动试验示意

图4 振幅测量示意

4 试验结果与分析

4.1 梁端振幅与电流频率的关系

4.1.1 试验数据分析

控制输入交流电压幅值为10 V，探究四种不同磁感应强度磁场下交流电频率对梁端振幅的影响。图5给出了交流电频率由10 Hz增大至200 Hz过程中，梁端振幅的变化规律，由图可知四组频率—曲线走向大致相同，频率从10 Hz开始增大的过程中，梁端振幅先增大后减小，频率大概为50 Hz处，振幅达到最大。

图5 振幅与频率曲线

利用有限元模态分析方法，得到本次试验简支微梁结构一阶固有频率为45.945 Hz。可得产生上述趋势的原因：当输入电流频率接近结构固有频率时，结构振幅不断变大，当电流频率达到固有频率45.945 Hz时，系统发生共振，振幅达到最大。

4.1.2 振动模型分析

微梁变形较小，且处于弹性范围，可近似认为微梁中部位移与梁端位移存在比例关系，二者比例系数为φ=20 mm/10 mm=2。故由式(6)得微梁梁端振幅

(7)

考虑到同一磁场中，即同一永磁体间距时，磁感应强度B不变，当电流角频率为ω1时，得到梁端振幅为y1，改变电流角频率为ω2，得到梁端振幅为y2。定义振幅比为η12=y1/y2，电流频率变化过程中，磁感应强度B、电流最大值Im等参数均保持不变，两式相比均可消去，由式(7)得到

(8)

由式(8)可知，振幅比η只与电流频率相关，可反映电流频率对梁端振幅的影响规律。同一永磁体间距条件下，令10 Hz初始电流频率时的振幅为基本幅值y2，其他频率时的振幅为y1，得到的一系列试验振幅比η，同样由式(8)也可得到理论振幅比η，如图6所示。

图6 振幅比η与电流频率曲线

可以看出，随着电流频率的增大，振幅比η先增大后减小；输入电流频率小于50 Hz或大于100 Hz时，理论模型振幅比曲线可以很好拟合试验振幅比曲线；而电流频率介于50～100 Hz之间时，理论模型与试验结果有较大差别；造成上述变化趋势的原因如下：本次研究建立的理论模型为无阻尼状态下的简支梁模型，而实际试验过程中存在空气阻力，电流频率介于50～100 Hz之间时，微梁振幅相对较大，同时运动速度相对较快，空气的阻尼效果比较明显。

图6同时反映出输入电流频率小于50 Hz或大于100 Hz时，理论振动模型式(7)可以很好地反映微梁实际振动过程中的振幅变化规律。

4.2 梁端振幅与输入电压的关系

控制输入交流电频率为50 Hz，在四种不同磁感应强度磁场中，探究输入电压对梁端振幅的影响。图7给出了输入电压由10 V减小至1.2 V过程中，梁端振幅的变化规律如图7所示，交流电压最大值从1.2 V增大到2 V的过程中，振幅迅速增大；电压最大值高于2 V以后，幅值缓慢增大。可以看出，当交流电压最大值大于2 V以后，电压对于振幅的影响相对较小，因此,本文提出的电磁驱动器方案具有低驱动电压,也可以实现大振幅的优势。

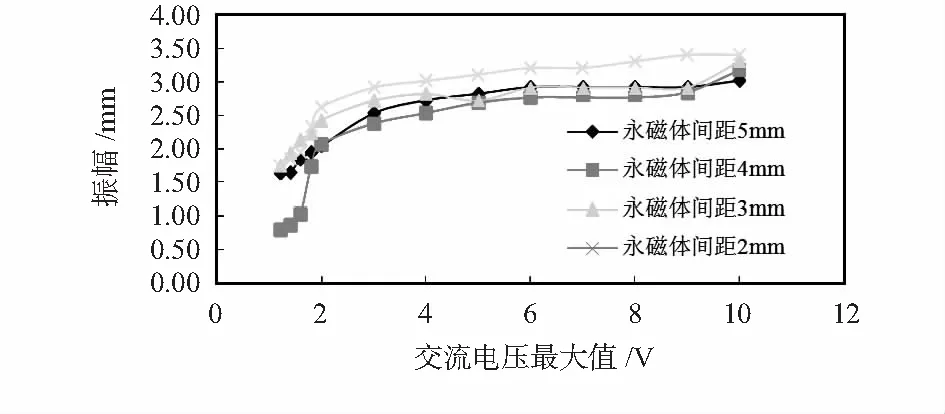
图7 梁端振幅与输入电压

4.3 梁端振幅与磁感应强度(永磁体间距)的关系

控制输入电压最大值为10 V，在不同输入电流频率条件下，探究不同磁感应强度(即不同永磁体间距)对梁端振幅的影响。图8给出了永磁体间距由2 mm增大至5 mm过程中，梁端振幅的变化规律。可知，当永磁体间距减小，即磁感应强度增大时，梁端振幅不断增大，这种趋势在较低输入电流频率下尤为明显。

图8 梁端振幅与永磁体间距曲线

5 结 论

本文针对微扑翼飞行器提出一种新型电磁驱动器方案，为探究驱动器微梁的振动特性，建立了电磁场中微梁振动模型，在此基础上设计了电磁驱动的微梁振动试验。结合理论振动模型与试验结果，发现在较低驱动电压、较大磁感应强度条件下，调整输入交流电频率至微梁驱动器系统的固有频率，即可实现微梁较大幅度的拍打振动，凸显了电磁驱动器驱动力大、驱动电压低、功耗小的优点。该结果为后续微型扑翼飞行器电磁驱动器的优化研究奠定基础。