Miura折叠超材料在简谐激励下的振动响应

张大鹏，周 翔

（上海交通大学 航空航天学院，上海 200240）

折叠结构普遍存在于自然界中，如树叶，昆虫翅膀等。而随着折叠结构研究的发展，目前折叠结构已被广泛的应用于工程中，包括：空间可展结构、变形建筑、冲击罐、夹芯结构、隔声及隔热材料、机械二极管、人工肌肉等。折叠超材料是基于折叠结构发展而来，具有超常的物理性能。

目前，对于折叠超材料的研究大多集中于Miura折叠超材料以及由它衍生出来的各种变化形式，主要研究其静态和准静态力学性能[1-3]。而国内外对于折叠超材料的动力学分析很少。Fang H.等人研究了一种具有自稳定特性的Miura折叠超材料结构，试验分析表明，该结构具有丰富的动力学响应，可以通过调整折痕刚度来设计[4-5]。Sadeghi S.等人通过在折叠结构中密封压缩空气，设计了一种具有准零刚度特性的Miura折叠超材料结构，建立弹簧-质量等效模型进行分析，发现该结构可以提供有效的低频隔振[6]。Yasuda H.等人将Tachi-Miura polyhedron(TMP)管状折叠超材料简化成多连杆结构和弹簧-质量模型的等效分析模型，研究了该超材料的冲击响应，发现作用于一端的冲击载荷在内部以小振幅稀疏波的形式传播，展现出该超材料良好的抗冲击特性[7-8]。

国内外对折叠超材料的动力学分析中，大多数将模型简化为弹簧、多连杆等等效模型，缺少实际模型的系统特征。本文在ADAMS中建立了Miura的真实模型，分析了典型的三种结构模型，在力和位移两种简谐激励下，不同折痕刚度对Miura折叠超材料振动响应的影响。

1 模型的建立

1.1 建模

由于实际结构中，面元刚度远远大于折痕刚度，变形主要通过折痕的转动来进行，本文将平行四边形的面元设置为具有质量和刚度的平行四边形刚性壳体，折痕为转动铰和无预载的扭转弹簧来讨论。ADAMS是全球运用最为广泛的机械系统仿真软件，拥有强大的刚体动力学分析功能。本文使用CATIA建立模型，导入ADAMS进行无重力模拟仿真。假设每个Miura单元内部折痕具有相同的扭转弹簧刚度ka。图1为由单个Miura单元构成的单层Miura模型。

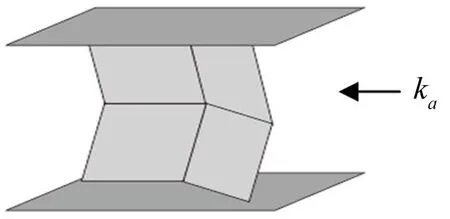
图1 单层Miura模型

将扭转弹簧刚度分别为ka和kb，连接处折痕的扭转弹簧刚度为kc的两个Miura单元组合得到双层Miura模型，如图2。

图2 双层Miura模型

标准的Miura折叠结构是仅有单一自由度的结构，在分析单自由度Miura结构的同时，本文设计了一种由Miura单元和分隔面组合构成的多层堆叠Miura模型：多个Miura单元格纵向堆叠，它们之间由无质量、无厚度的刚性面分隔开来，这些分隔面允许Miura单元在表面滑动，有且仅有纵向位移一个自由度，如图3。我们定义由上至下的奇数单元和偶数单元的扭簧刚度相同，分别为ka和kb。

1.2 激励类型

本文中对结构施加两种类型的激励：简谐力和简谐位移，在ADAMS中分别定义Force和Motion。相对应的边界条件分别为上表面加载简谐力，底边固支；上表面加载简谐位移，下表面自由运动。为了得到不同频率下的振动响应，频率的取值范围定为0.01 Hz到100 Hz，并将频率值取对数，等分成41组数据；每种频率下分析步骤为1 000步，分析时间定为当前简谐激励的20个完整周期。

简谐力定义为

图3 多层堆叠Miura模型

其中：F0表示力的幅值，ω表示频率,t表示时间。

简谐位移定义为

其中：X0表示位移的幅值，ω表示频率,t表示时间。

本文讨论的范围如下。

1.3 结果处理方法

考虑到Miura折叠机构的动力学响应可能存在高度的非线性，对ADAMS导出的分析结果采用两种方式进行处理。对于简谐力激励，定义响应力的幅值

其中：Fmax和Fmin表示响应力随时间变化的最大值和最小值。

对于简谐位移激励，将响应位移的均方根除以激励位移的均方根，得到位移传递值。

其中：xi和yi(i=1,2,3,…,N)表示响应位移在不同时刻下的位移变化和激振器的位移变化。

2 结果及分析

2.1 单自由度模型在简谐力激励下的振动响应

单层Miura模型由单个Miura单元构成，设置不同折痕刚度，分析其频率响应，具体参数见表1。

图4表明，在简谐力的作用下，响应力的幅值随频率变化均呈现三个阶段：第一个阶段在低频率激励下，响应力的幅值和激励力的幅值基本一致；第二阶段，由于系统中折痕不设置阻尼，当系统在发生共振的时产生较大的振动，响应力的幅值远远大于激励力的幅值；而在第3阶段，频率继续增加，响应力的大小持续减小。

表1 三种模型的刚度参数

通过改变折痕刚度，可以得到不同的共振频率，而最大响应力幅值随着折痕刚度的增加而增加，直到达到上限。需要注意的是，当折痕刚度减小到一定数值时，系统共振时会使得结构完全折叠，应避免折痕刚度设置得过小。

双层Miura模型由两个Miura单元构成，设置第二个单元的不同折痕刚度，分析不同刚度组合的频率响应。图5表明，在简谐力的作用下，双层Miura模型的频率响应与单层Miura模型相比，在不同阶段响应力的变化趋势相类似。通过改变第二个Miura单元的折痕刚度，可以得到不同的共振频率，但敏感性较低。而通过不同刚度组合，相较于较大折痕刚度的单元，组合刚度降低，最大响应力幅值增大。

2.2 多自由度模型在简谐力激励下的振动响应

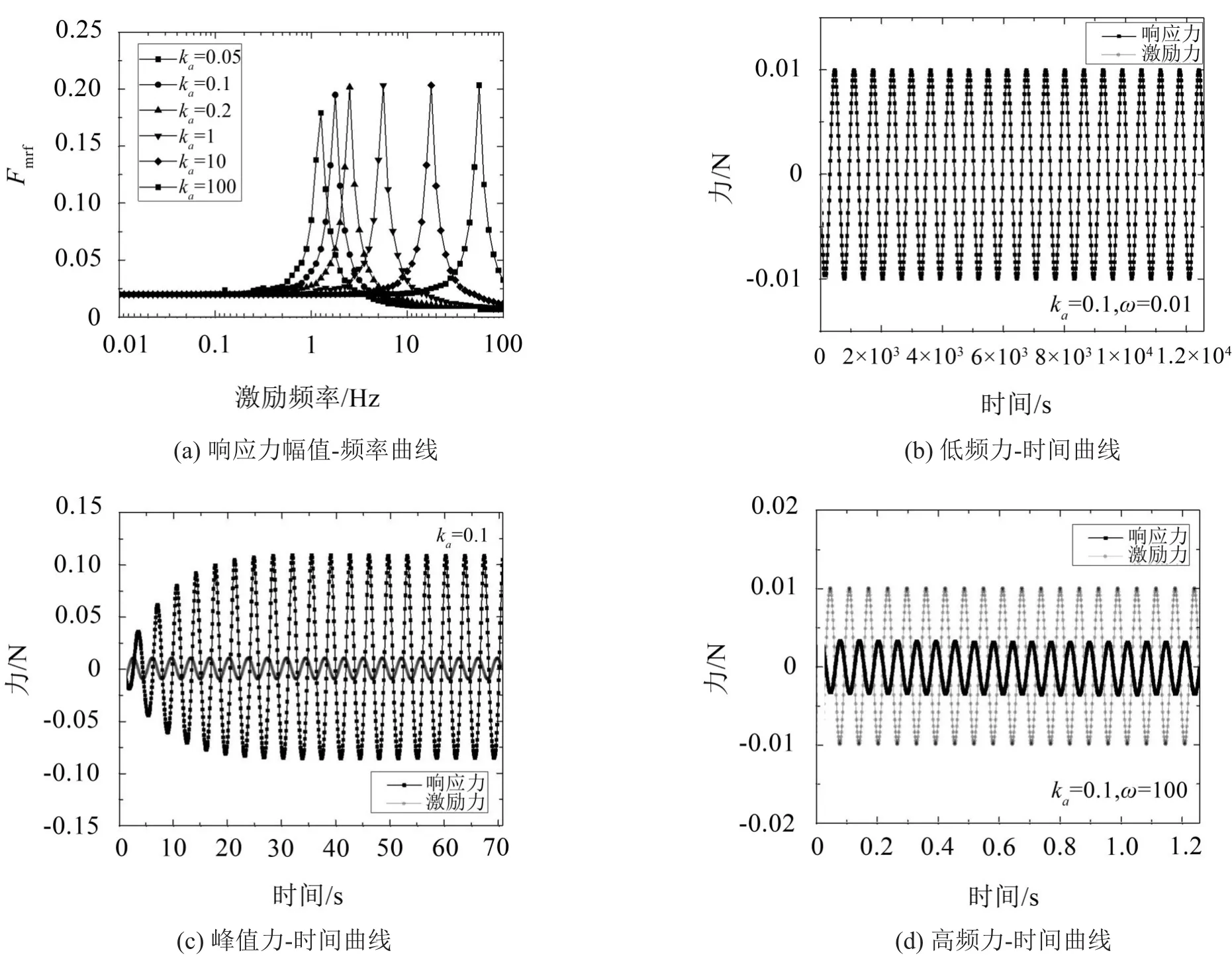
图4 单层Miura模型

多层堆叠Miura模型由相互隔离的Miura单元堆叠形成，具有多个自由度。堆叠数量分别取2、3、4，分析不同堆叠数量的频率响应。在激励作用下，模型不同层面的Miura单元的变形是不同步的，存在部分单元伸展而部分单元压缩的情形。

图6表明，随着堆叠数量的增加，模型固有频率数量增加，最大振动响应幅值增加，而最大响应力幅值对应频率降低。在共振频率区间外，几种模型的激励响应幅值基本一致。

图5 双层Miura模型响应力幅值-频率曲线

图6 多层堆叠Miura模型响应力幅值-频率曲线

2.3 单自由度模型在简谐位移激励下的振动响应

单层Miura模型和双层Miura模型在简谐位移激励的作用下，频率响应(如图7、图8)显示了和简谐力激励作用下相同的变化趋势：位移传递值在低频段为1，达到共振时，位移传递值最大值对应频率下，位移响应的幅值远大于激励幅值，继续增加激励频率，位移传递值小于1。

图7 单层Miura模型位移传递值-频率曲线

单自由度模型在两种简谐激励下，振动响应类似，通过适当改变折痕刚度，改变其共振频率，可以达到很好的低频隔振效果。

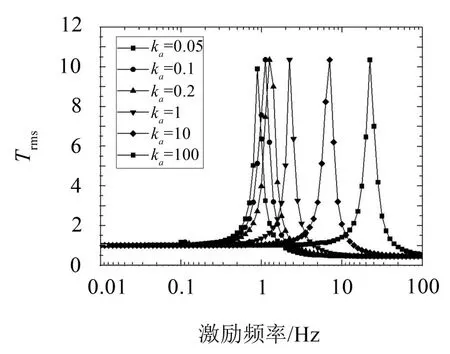
图8 双层Miura模型位移传递值-频率曲线

2.4 多自由度模型在简谐位移激励下的振动响应

多层堆叠Miura模型取10个堆叠单元，分析其不同响应峰值下的位移-时间曲线。在简谐位移激励的作用下，随着激励频率的不断增加，激励与响应之间的时间间隔逐渐增加，当频率增加至一定数值时，底部面元响应的时间超过激励周期的20倍，而使得位移传递值为零，见图9。

3 结语

本文应用ADAMS分析典型的三种结构模型，在力和位移两种简谐激励下，不同折痕刚度对Miura折叠超材料振动响应的影响。结果表明，单自由度结构的Miura构形在两种激励下频率响应类似，通过改变折痕刚度可以改变其共振频率，达到很好的低频隔振效果。多自由度模型可以通过增加堆叠数量降低共振频率。

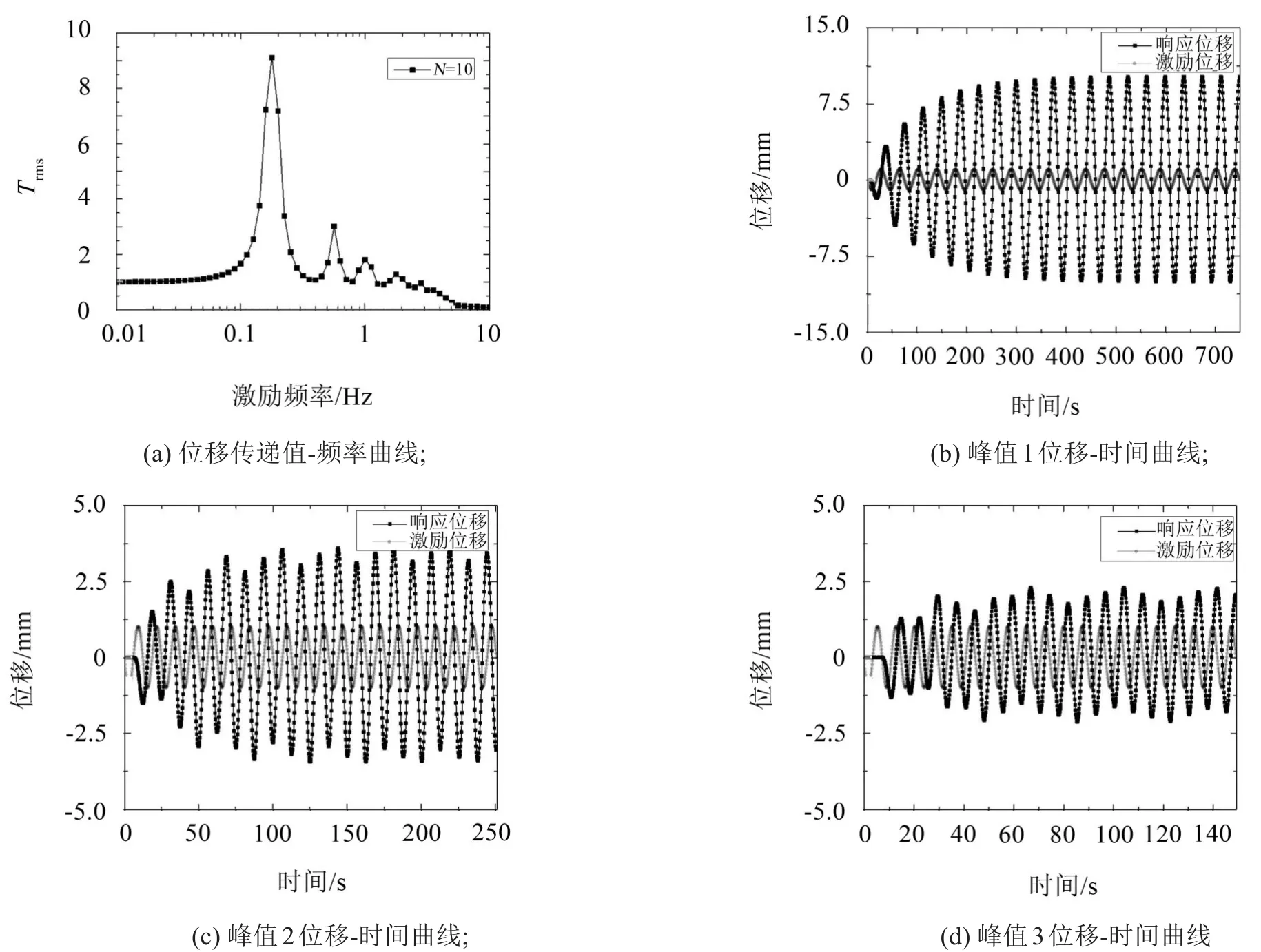
图9 多层堆叠Miura模型