不同激励下双层底振动传递特性研究

2019-03-05张冠军姜超君

噪声与振动控制 2019年1期

何鹏，向阳，郭宁，张冠军，姜超君

（1.武汉理工大学能源与动力工程学院，武汉 430063；2.船舶动力系统运用技术交通行业重点实验室，武汉 430063）

双层底结构是现代水面船舶典型的结构形式之一，船上的众多机械设备在运转时产生的振动通过基座-双层底进行传递，导致船舶向外辐射噪声。而底桁和实肋板是双层底结构内外底板的主要连接构件，也是振动在内外底板传递的基本途径，其振动传递特性在很大程度上决定了船舶的振动噪声水平。

目前国内外学者从结构声强的角度对结构的振动传递特性和能量分布进行了一定的研究，早在1990年，SA Hambric就推导了梁和板结构功率流表达式，并用Nastran计算了结构的输入输出功率[1]；Dae-Seung Cho使用结构声强结合有限元的方法对阶梯板在不同边界条件和激励下的能量流动分布进行分析[2]；Khun M S研究了平板布置阻尼器及平板间模拟螺栓连接的板的能量分布[3]。李凯针对船舶上的各种加筋板形式，研究了振动能量在加筋板上的传递和分布特性，以舰船平台板架验证声强理论的应用价值[4]；王海军计算了三维水电站厂房结构的结构声强，得到不同载荷下的厂房振动传递路径[5]；乔志基于有限元功率流理论，计算了L型板结构的振动功率流，并提出了功率流传递率作为振动传递的指标，将功率流可视化技术应用到舱段结构中[6]；张雪冰为了对变压器油箱实现在线监测，运用板壳功率流理论对变压器油箱的振动传递途径进行分析，为监测系统的测点布置提供了指导[7]；宋玉超、秦文等人对双层底结构的模态特性进行了研究[8-9]；朱成雷根据阻抗失配原理改变了双层底的连接结构和添加阻振质量块，通过阻断波的传递来提高隔振效果[10]。目前为止，针对不同激励下双层底的振动研究较少，本文将结构声强分析方法应用于双层底结构的传递路径识别中，并依此添加阻振质量来降低双层底结构的振动，所得结论对船舶振动传递路径的识别和振动控制具有参考意义。

1 板壳结构的结构声强分析

船舶的双层底结构是典型的板壳结构，可以用板壳理论来描述其动力学特性。板壳结构的结构声强表示结构上某点能量的大小和方向，对于薄板来说，可以认为通过其单位宽度上的功率流即为结构声强，其本质上表示功率流密度。时域上瞬时结构声强的定义为

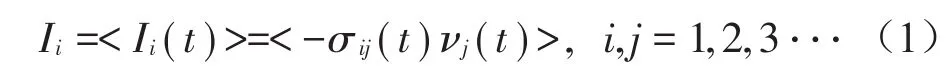
式中：σij(t)，vj(t)分别为t时刻j方向上的应力分量和速度分量，<·>代表时间平均量。

通过结构的能量流In可以对第n阶瞬时结构声强In(t)进行时间平均得到

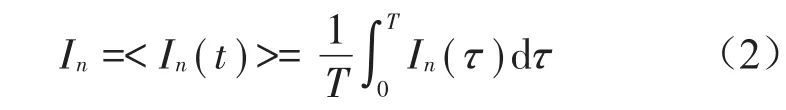
经过傅里叶变换即可得到频域内结构声强的表达式

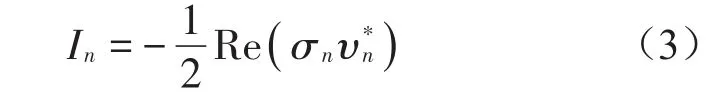
式中：Re表示复数取实部，σn为频域内的复应力为速度共轭。

根据单元中的内力以及相应的速度表达式，对于频域内稳态振动的二维平板结构，板单元的结构声强在x和y方向可表示为

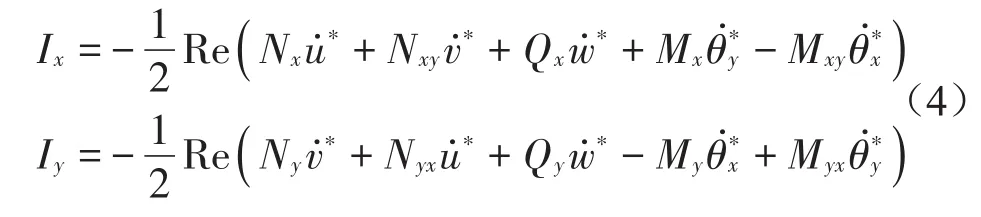
对于简谐振动下的结构，位移形式下的结构声强表达式为

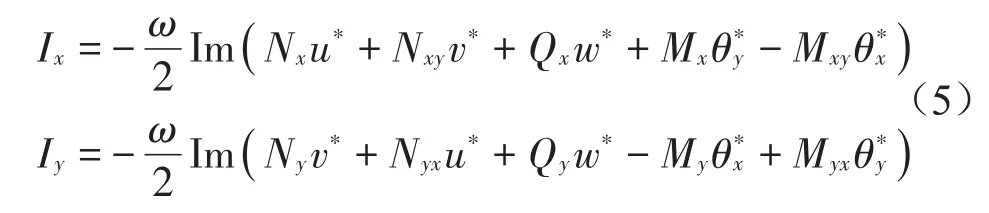
式中：ω为圆频率，Re表示取实部，Im表示取虚部，Nx，Ny，Nxy=Nyx为薄膜力；Mx，My，Mxy=Myx为弯矩和扭矩；Qx，Qy为剪力；u*，v*，w*为x，y，z方向平动位移的复数共轭；θx*，θy*为x，y方向转动位移共轭。

2 双层底结构振动响应计算

2.1 有限元模型

双层底结构是由内底板、外底板、底桁、实肋板、纵骨组成，内外底板通过底桁和实肋板连接，并且布置有密集的纵骨，以提高船舶底部的纵向强度。双层底的有限元模型见图1。

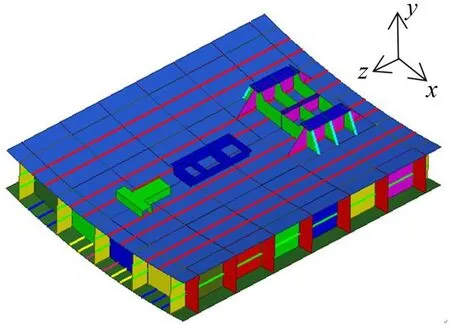
图1 双层底结构有限元模型

该双层底结构是截取某型舰艇的机舱简化而来，整个结构长3.40 m、宽2.74 m、高1 m，内底上沿中线位置依次布置了两个基座，分别是离心泵-电机基座、阻振基座，用以施加激励模拟实际情况。内外底板、底桁、实肋板等板结构采用SHELL181单元模拟，其他梁结构采用BEAM188单元模拟。有限元网格划分采用一个波长内6～10个单元的原则，模型最小板厚为8 mm，计算频率范围为20 Hz～400 Hz，要求有限元单元长度最大为0.244 m，本文的网格大小为0.02 m，满足上述要求。模型所用材料参数见表1。

表1 钢的材料属性

在进行振动响应计算之前，需对模型进行约束及边界处理，此处在双层底外底板建立四个弹性支撑，四周边界插入Drucker-Prager本构模型建立的沙箱模拟无反射边界条件，处理后的模型见图2。

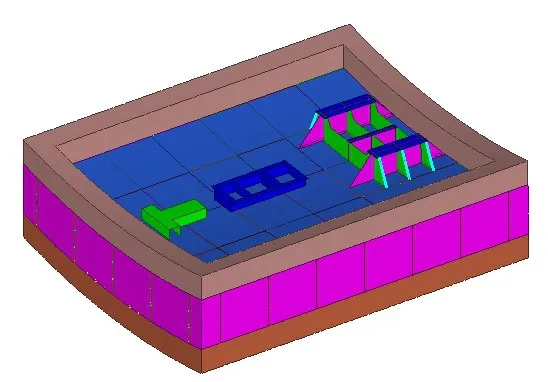
图2 双层底结构计算模型

为了方便下文对于底桁和实肋板的描述，对模型中底桁和实肋板进行编号，见图3，对一整块底桁或实肋板的标号如图中标示，依次表示为底桁-1－底桁-5、实肋板-1－实肋板-7，底桁或实肋板小块标号以底桁-1、实肋板-7的编号方向为例进行编号，下文采用该编号代表具体板块，不再赘述。

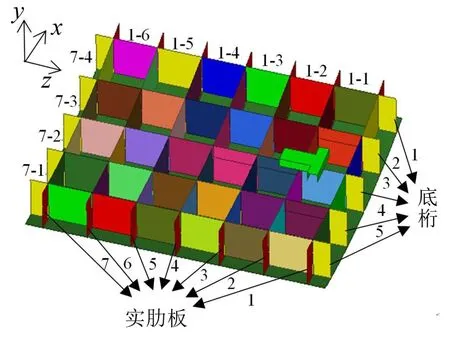
图3 底桁和实肋板编号示意图

2.2 谐响应计算

针对上述处理后的模型，分别进行单激励和多激励下的谐响应计算，在离心泵基座上施加的单激励为实测离心泵的机脚振动加速度结果，采用大质量法扩大106倍施加，测试现场和所得频谱见图4，多激励的施加则考虑到所施加的力便于模拟，且不造成模型单侧变形过大，故在离心泵激励的基础上在阻振基座上对称施加恒值力，平均离心泵激励的幅值作为阻振基座处激励幅值，同样采用大质量法扩大106倍，取1.5×107N，施加位置见图5，计算频率范围为20 Hz～400 Hz，使用完全法以1Hz间隔进行计算。

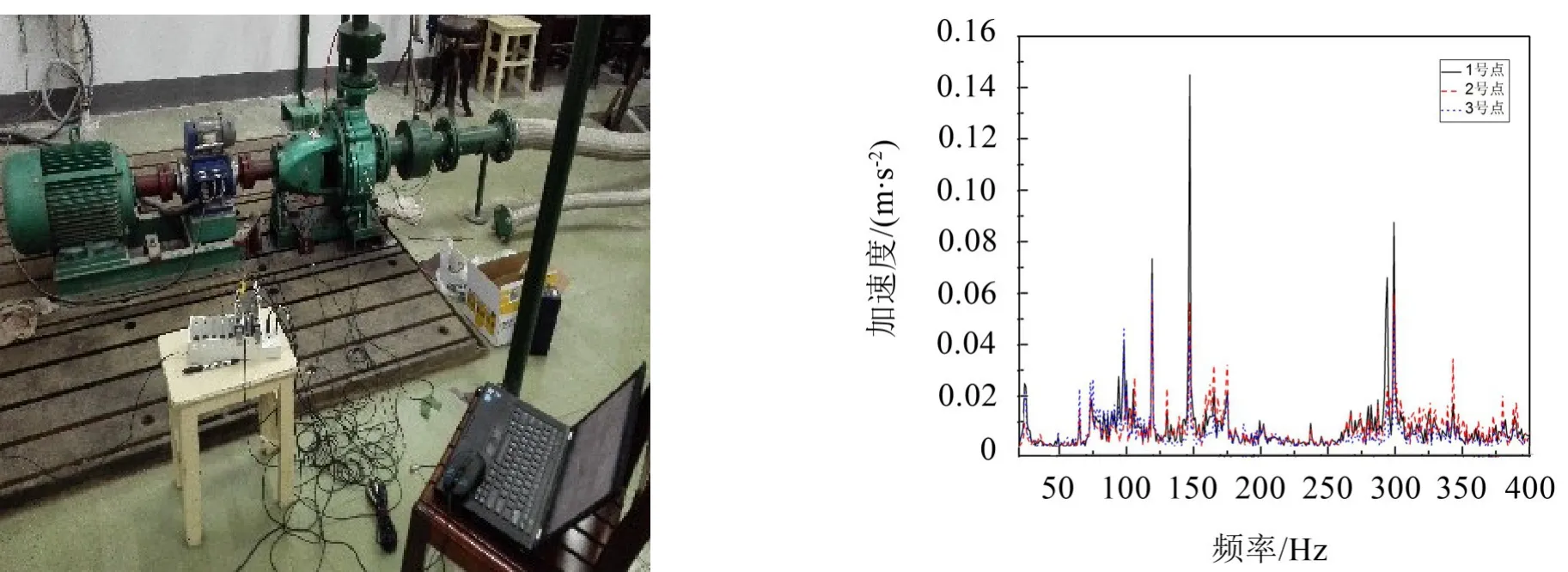
图4 离心泵测试现场及机脚激励谱

图5 激励施加位置

对于计算完成后的单激励与多激励模型，选取外板与底桁和实肋板连接处对称的7个节点作为评价点，如图6所示，提取评价点振动位移计算平均振动位移级，参考位移取1.0×10-12m，见图7－图8。

由外板评价点的振动位移级曲线可知，在计算频段20 Hz～400 Hz范围内呈现较多地峰值，单激励下的峰值主要有24 Hz、33 Hz、106 Hz、266 Hz、297 Hz，其中24 Hz跟33 Hz处的峰值最明显，多激励下的峰值主要是 24 Hz、87 Hz、158 Hz、263 Hz，其中24 Hz和87 Hz处最为明显，可以看到激励的改变使得整个双层底的频率响应峰值发生了变化，单激励下87 Hz处的波谷在多激励下变成了最大地响应峰值，说明新激励的施加位置刚好处在该频率处的最大振型处，引起结构在87 Hz处的峰值。

图6 外底板评价点位置

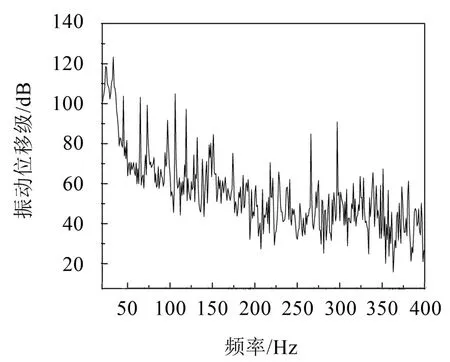
图7 单激励评价点平均振动位移级

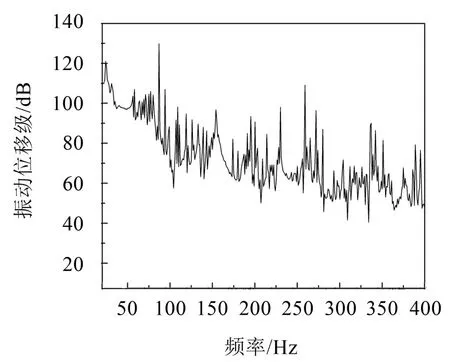
图8 多激励评价点平均振动位移级

3 结构声强计算与传递路径分析

根据振动响应结果，分别对单激励下33 Hz及多激励下87 Hz的底桁和实肋板的结构声强进行计算，由公式5，使用APDL命令流在ANSYS中提取节点和单元的位移、应力信息，由于ANSYS输出的应力是针对单元的，而位移数据是节点处的，此处将SHELL181单元的四个节点位移数据取平均，等效为单元位移进行计算。为了更直观地比较各实肋板与底桁的结构声强大小，计算所有底桁（或实肋板）的结构声强和，单个底桁（或实肋板）的结构声强与底桁（或实肋板）结构声强和的比值大小定义为声强贡献度，即

式中：ci表示声强贡献度，Ii为第i个底桁（或实肋板）的结构声强，为底桁（或实肋板）的声强和，表2为不同激励下底桁和实肋板的结构声强和。本文关注的是振动波在内底和外底之间的传递，因此只关心Y方向的结构声强值。

由表2可知，底桁和实肋板的Y向声强值均为负值，即负值表示振动能量由内底传向外底，结合声强贡献度的计算公式，当贡献度为正时表示能量由内底正向传递给外底，反之是由于振动波的反射形成的逆向能量流动，正向流动的能量对外底板振动产生贡献，是导致双层底结构向外辐射噪声的主要原因。

表3是单激励和多激励下底桁和实肋板的结构声强值和贡献度。由上文知，贡献度为正代表正向的能量流动，由单激励下33 Hz的贡献度可知，贡献度排在前五的分别是实肋板-2、底桁-3、实肋板-1、底桁-2、底桁-4，其中实肋板-2的贡献度最大，是能量传递的最主要途径；多激励87 Hz下占主要的有实肋板-6、底桁-4、底桁-2、实肋板-1，其中实肋板-6的贡献度最大，成为能量贡献的主要途径。为了更直观地对相应底桁和实肋板的能量分布进行分析，在有限元中导出各底桁和实肋板中单元的坐标信息，结合计算的结构声强，利用MATLAB编程绘制结构声强矢量图，实现结构声强的可视化。

表2 不同激励下结构声强和/W

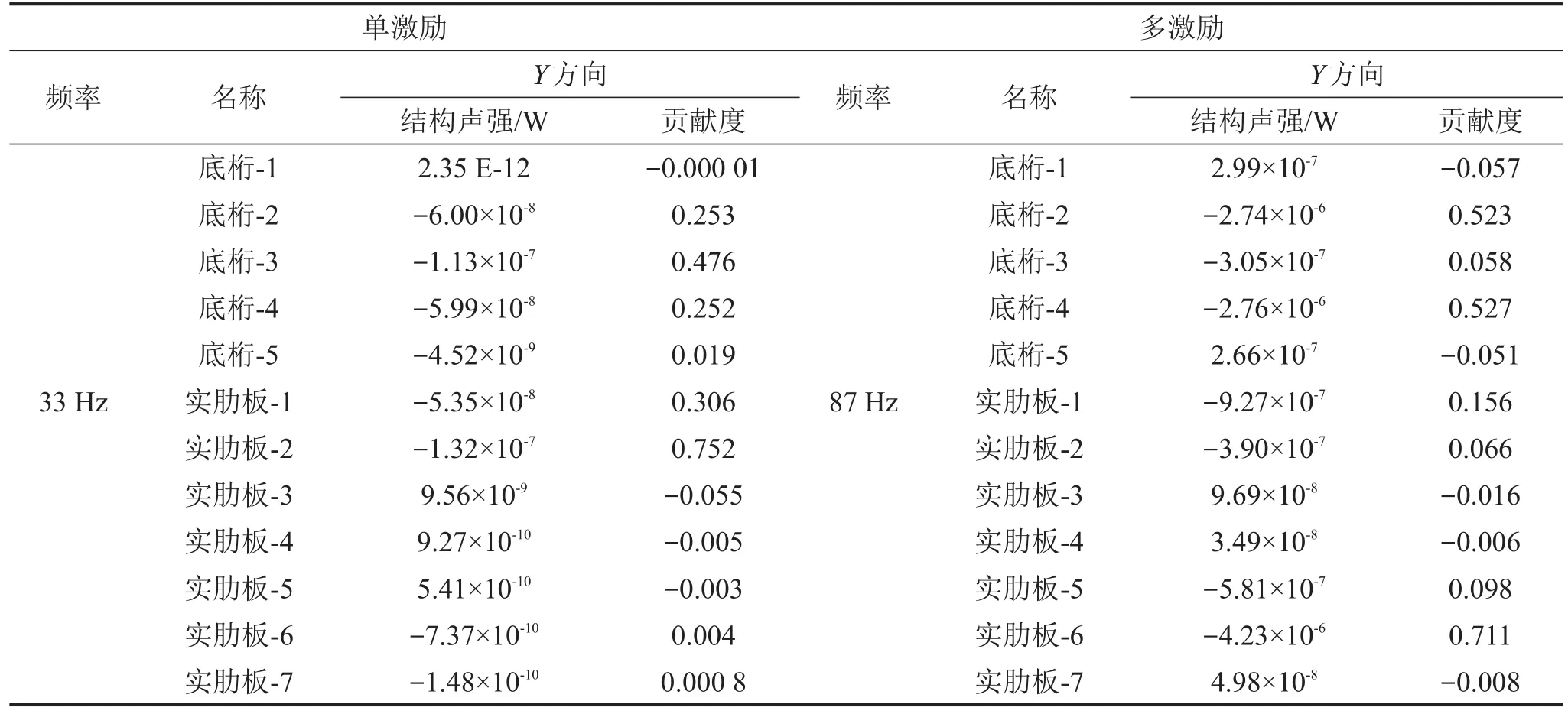
表3 单激励与多激励下底桁和实肋板的结构声强和贡献度

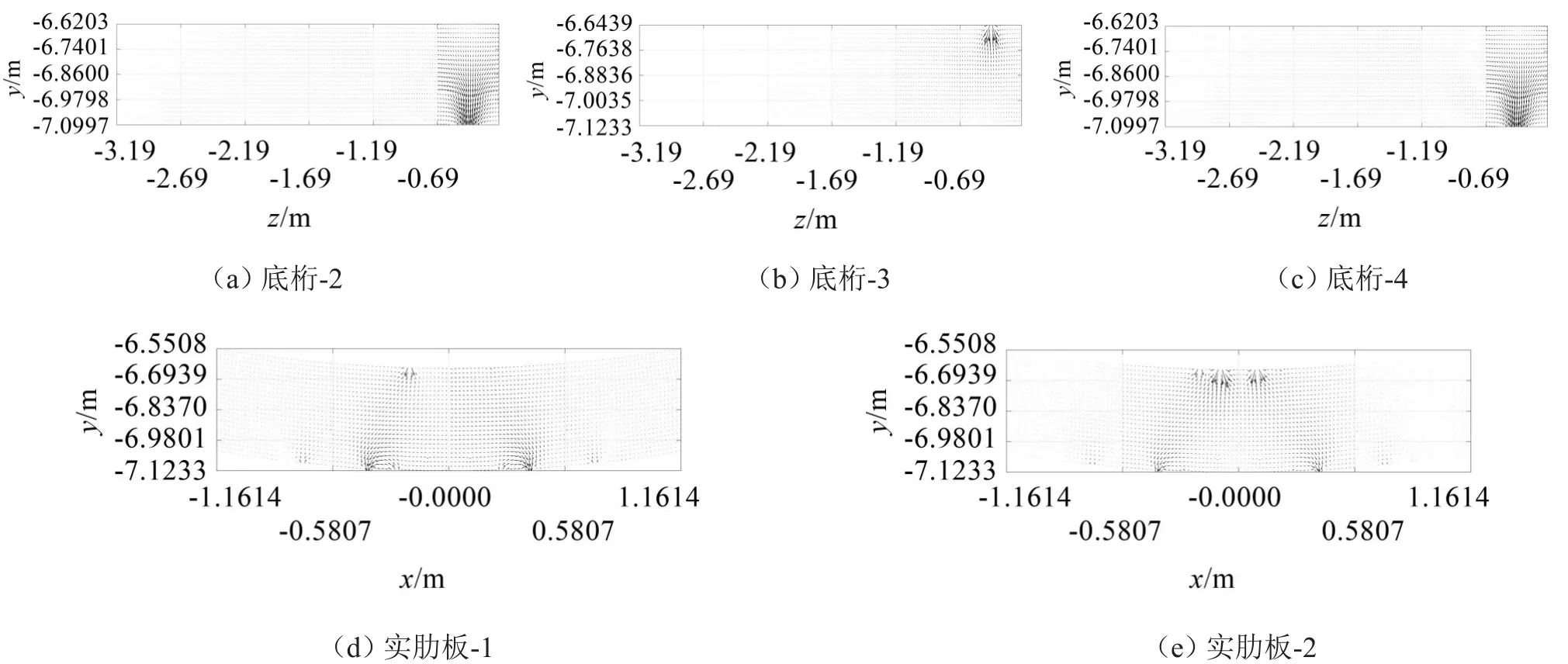
图9 单激励33 Hz底桁和实肋板声强矢量图

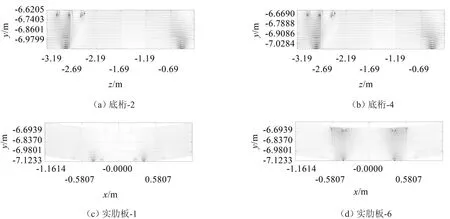
图10 多激励87 Hz底桁和实肋板声强矢量图

图9和图10中矢量图的箭头方向代表能量流动的方向，长度代表能量流的大小，从矢量图中可以清晰地看到能量流在板中的分布情况，参考上文板的编号可知，单激励33 Hz下底桁的能量流在靠近离心泵基座端（图片右端）最密集，实肋板在离心泵基座下方（图的中部）位置处最大，用编号表示即底桁-2-1、底桁-3-1、底桁-4-1以及实肋板-1-2、实肋板-1-3、实肋板-2-2、实肋板-2-3，该位置的三维示意图见图11。

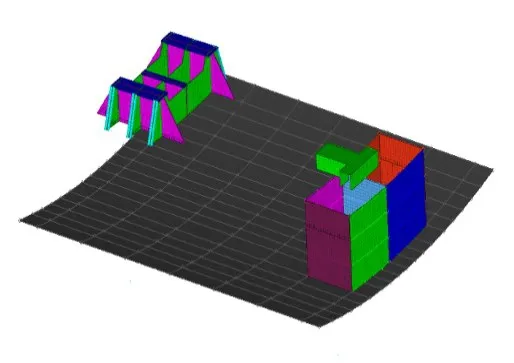
图11 单激励33 Hz传递路径

表示单激励下该频率的主要传递路径。同理，多激励下87 Hz下的能量流呈对称分布，即底桁-2-1、底桁-2-6、底桁-4-1、底桁-4-6、实肋板-1-2、实肋板-1-3、实肋板-6-2、实肋板-6-3为主要的传递路径，三维示意图见图12。

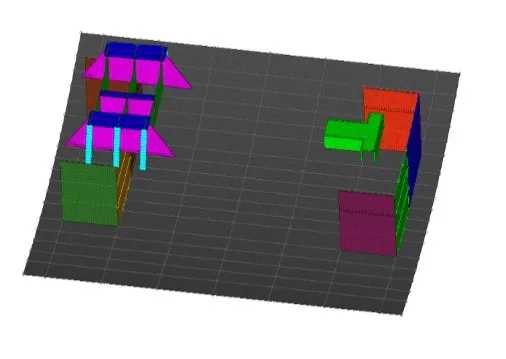
图12 多激励87 Hz传递路径

可以发现，不同激励下的主要传递路径都分布在激励源的正下方，越靠近激励源附近能量分布越密集，远离激励源的位置能量分布较稀疏，原因是板结构中振动波的自然衰减和板连接形式的变化影响了振动波的传递。

4 阻振质量设计及分析

针对上文辨识的主要传递路径，参照文献11，同时为了方便后续试验台架的加工，设计截面尺寸为40 mm×40 mm的偏心阻振质量块，材料为钢，阻振质量块与船体板之间为部分刚性连接，阻振质量块质量占模型质量的2%，布置于多激励下的主要传递路径上，布置形式见图13。

将附加阻振质量块的模型重新进行谐响应计算，得到外板评价点的平均振动位移级，见图14。

为了更好地评价在主传递路径上附加阻振质量块的减振效果，采用边界元方法对多激励阻振前后的双层底结构的声功率级进行计算，外板的辐射声功率级曲线见图15。

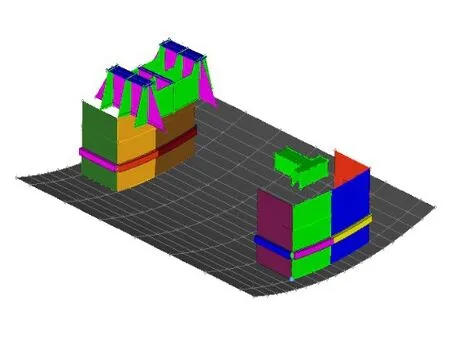
图13 阻振质量块布置形式

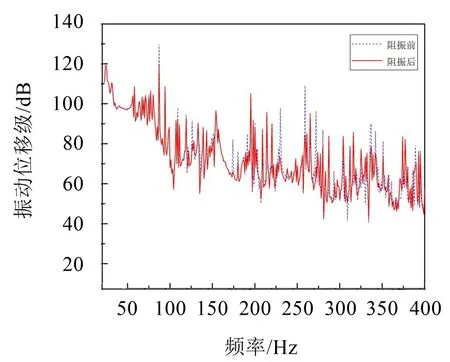
图14 阻振前后外板振动位移级

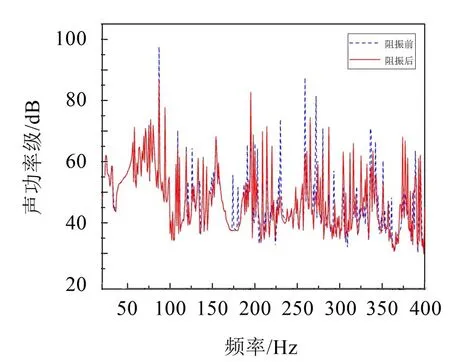
图15 阻振前后外板声辐射

从外板的振动位移级来看，在87 Hz、230 Hz、259 Hz、272 Hz处均有较大的降低，在20 Hz～150 Hz频率处范围内，除了87 Hz以外，其余频率范围处的曲线没有太大变化，200 Hz以后的频段内的振动位移级有较大幅度的降低，但同时也造成了一些频率处振动位移的增大，原因是阻振质量块的加入阻隔了主传递路径上振动波的传递，同时由于波的反射导致200 Hz以上一些频率振动位移的增大。外板声功率级曲线的峰值频率与振动位移级曲线的峰值频率基本一致，在以上4个频率处分别降低了10.62 dB、25.58 dB、24.77 dB、31.3 dB，其中在170 Hz～190 Hz内形成了一个减振带；同样，200 Hz以后的频段声功率级既有降低也有增大，对声辐射的计算结果在计算频带内合成，阻振前为98.26 dB，阻振后为90.06 dB，在整个频段内的声功率级降低了8.2 dB，说明在振动的主传递路径上布置阻振质量块对于振动的控制有明显的效果。