基于热湿交换理论的巷道风流温、湿度影响因素研究*

张一夫，倪景峰，戴文智

(1.湖南工学院 安全与环境工程学院，湖南 衡阳 421002；2. 辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛 125105；3. 辽宁工程技术大学 机械工程学院，辽宁 阜新 123000)

0 引言

随着矿井开采深度的增加，矿井热害问题愈加严重，已经成为矿产开采中1个亟待解决的问题[1-2]。在一些深部矿井中，高温、高湿的自然条件严重地影响和危害着矿业工人的身体健康。因此，准确预测矿井风流温、湿度的变化规律、正确评价高温矿井的热害程度对改善井下作业环境、保证煤矿安全开采具有非常重要的意义。

相关研究表明[3-4]，矿井风流热力参数的变化主要受风流与围岩之间的热交换和湿交换的影响。其中，围岩与风流之间的热交换是影响风流干球温度变化的主要因素，而其他形式的热源，如机电散热、人员散热等热源由于其位置比较分散，会导致井下局部位置风流温度的增加。湿交换是由于在采掘过程中伴随着大量的水分蒸发，导致风流湿度增加。在潮湿巷道中，壁面水分的蒸发会吸收大量的汽化潜热导致风流湿球温度的增加，而其他形式的分散的湿度源，如除尘水幕，矿井涌水等也会导致局部风流湿度的增加。

目前，国内外许多学者在风流温度、湿度预测方面进行了大量的研究工作，提出许多预测井下风流参数的有效方法[5-6]。其中，刘景秀等[7]以干燥巷道为例，研究围岩导热系数对风流温度的影响；侯棋棕等[8]依托热湿交换理论建立了围岩与风流间热湿交换的温度与湿度预测的理论模型，将风流温度与湿度间的变化关联起来；刘何清等[9]进一步建立热湿交换耦合计算关系式，发展了煤矿巷道传热传湿计算的简化模型；高建良等[10]则采用湿度系数法对壁面水分蒸发进行了处理，建立了在考虑壁面水分蒸发情况下风流与围岩间热湿交换的数学方程，利用有限差分法解算出围岩温度分布、壁面温度和围岩散热量的变化规律。本文在前人研究的基础上，充分考虑围岩温度场、壁面水分蒸发对风流参数的影响，建立贴体坐标系下围岩三维温度场的数学模型，并利用传热传质理论将围岩内部的导热问题与风流、围岩间的热湿交换耦合起来，以大柳塔煤矿52505综采工作面、进顺和回顺为例，通过数值模拟准确预测了巷道风流温、湿度的变化及分布规律。

1 热交换方程

围岩通过对流换热方式将一部分热量以显热形式传递给空气，导致空气干球温度上升，同时还通过壁面水分蒸发(传质)的方式将另一部分热量以潜热的形式传递给空气，导致空气湿球温度上升。因此，对于围岩而言，通过巷道壁面所传递的总热流密度qw为：

qw=qs+ql

(1)

式中：qs为风流吸收的显热热流密度，J/(m2·s)；ql为风流吸收的潜热热流密度，J/(m2·s)。

1.1 描述围岩温度场的三维数学模型

由于围岩内部温度场在靠近巷道一侧存在1个变温区[11]，变温区内存在着温度梯度，变温区外围岩保持着原始岩温。变温区内的围岩温度场满足三维导热控制方程：

(2)

式中：t为时间，s；x，y，z为三维空间3个坐标轴；cp为风流的定压比热，J/(kg·℃)；λ为围岩导热系数，J/(m·s·℃)。

根据矿井实际情况，可确定物理模型(如图1)边界条件为：r=ra，qw=-λ∂t/∂r和r=r∞，t=t∞。其中，ra为巷道等效半径，m；r∞为围岩变温区的厚度，m；t∞为围岩的原始岩温，℃；λ为围岩导热系数，J/(m·s·℃)。

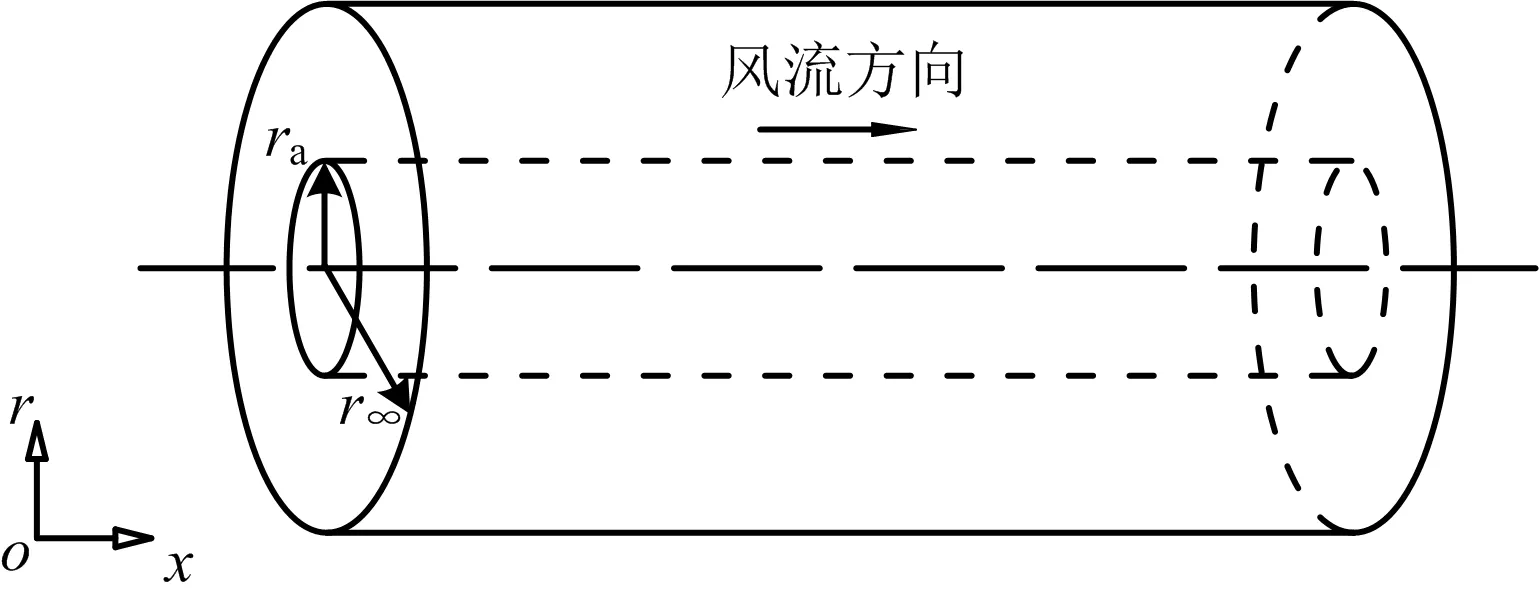
图1 水平巷道内风流流动的物理模型Fig.1 Physical model of airflow in horizontal tunnel

1.2 风流与围岩之间的显热交换方程

风流与围岩之间的显热交换主要以发生在巷道壁面的对流换热为主，其换热量可按下式计算：

qs=α(tw-tf)

(3)

式中：qs为风流吸收的显热热流密度，J/(m2·s)；tw为巷道壁面的温度，℃；tf为风流平均温度，℃；α为壁面的对流换热系数，J/(m2·s·℃)，其数值可参考文献[12]给出的计算公式：

α=8.4δMb0.8U0.2/S

(4)

式中：Mb为风流的质量流量，kg/s；δ为壁面粗糙度，m；U为巷道周长，m；S为巷道截面积，m2。

1.3 风流与围岩之间的潜热交换方程

风流与围岩之间的潜热交换是由于壁面水分的蒸发(或凝结)而引起的汽化潜热(或凝结热)所导致的。湿交换过程中的传热传质方程如下：

(5)

式中：Mb为风流的质量流量，kg/s；Lv为水的汽化潜热(或凝结热)，J/kg；df为风流含湿量，kg/kg干空气；ra为巷道等效半径，m；ql为风流吸收的潜热热流密度，J/(m2·s)。根据文献[3]，ql可写成:

ql=fσLv(dw-df)

(6)

式中：f为巷道潮湿覆盖率，无量纲；dw为壁温tw下的饱和含湿量，kg/kg干空气；σ为巷道壁面的湿交换系数，kg/(m2 .s),可根据Lewis公式[13]计算，公式如下：

(7)

式中：cp为风流的定压比热，J/(kg·℃)；Sc，Pr分别为风流的Schmidt数和Prandtl数。

2 方程组的离散和求解

由于物理模型的对称性，本文利用贴体坐标系建立围岩三维温度场的物理模型，如图2(a)所示。通过对控制方程的转换，在计算平面内(如图2(b))对方程组进行离散和求解(具体步骤见2.1节)。

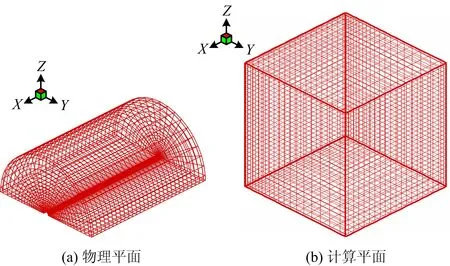
图2 围岩的几何构形及其网格划分Fig.2 Geometrical configuration and mesh generation

靠近风流一侧围岩壁面的温度值对整个解算过程至关重要。为了准确计算出围岩壁面的温度，对围岩壁面附近网格进行了逐级加密，径向局部网格逐级加密如图3所示。

图3 径向局部网格逐级加密Fig.3 Local mesh refinement step by step in radial direction

2.1 贴体坐标系下求解围岩温度场

依据链导规则、函数导数与其反函数导数间的关系[14]，将物理平面的控制方程式(2)转换到计算平面中，得到对应计算平面上的温度场控制方程：

(8)

式中：cp为风流的定压比热，J/(kg·℃)；t为时间，s；ρ为风流气体密度，kg/m3；J为Jacobi因子，代表了计算空间中控制容积的膨胀程度，其表达式为：

(9)

式中：α，β，γ为计算平面与物理平面之间的转换因子，表示如下：

(10)

利用有限容积法[15]对计算平面下的控制方程进行求解，温度梯度项采用二阶精度的中心差分格式进行离散。

2.2 井巷风流状态参数的求解

描述矿井风流显热交换的一维稳态方程为：

(11)

式中：Mb为风流的质量流量，kg/s；cp为风流的定压比热，J/(kg·℃)；tf为风流平均温度，℃；ra为巷道等效半径，m；qs为风流吸收的显热热流密度，J/(m2·s)。

依根据相邻节点间的温度变化与热交换关系，可得下风侧相邻节点处风流温度tf为：

(12)

式中：下标i为节点位置，i=1,2,…,n，n为节点个数。

同样，依据相邻节点间的含湿量变化与湿交换关系，可得下风侧相邻节点处风流含湿量df为：

(13)

忽略风流中水蒸气含量变化对风流密度的影响，则水蒸气分压力pv与含湿量df近似满足关系：

pv,i/pv,i-1=df,i/df,i-1

(14)

式中：pv为风流中水蒸气的分压力，Pa，其值可由下式计算：

pv,i=df,i·(pa,i-pv,i)/0.622

(15)

式中：pa为风流的大气压力，Pa。进而，可求得相应节点处风流相对湿度值φ为：

φi=pv,i/pb,i

(16)

式中：pb,i为节点i处风流当前温度下水蒸气的饱和分压力，Pa。

2.3 求解步骤

围岩温度场与矿井风流间的热湿交换耦合问题，可通过温度场的模拟计算与围岩边界条件的更新迭代过程实现。采用 C++语言完成程序编制，具体计算流程如图4所示。

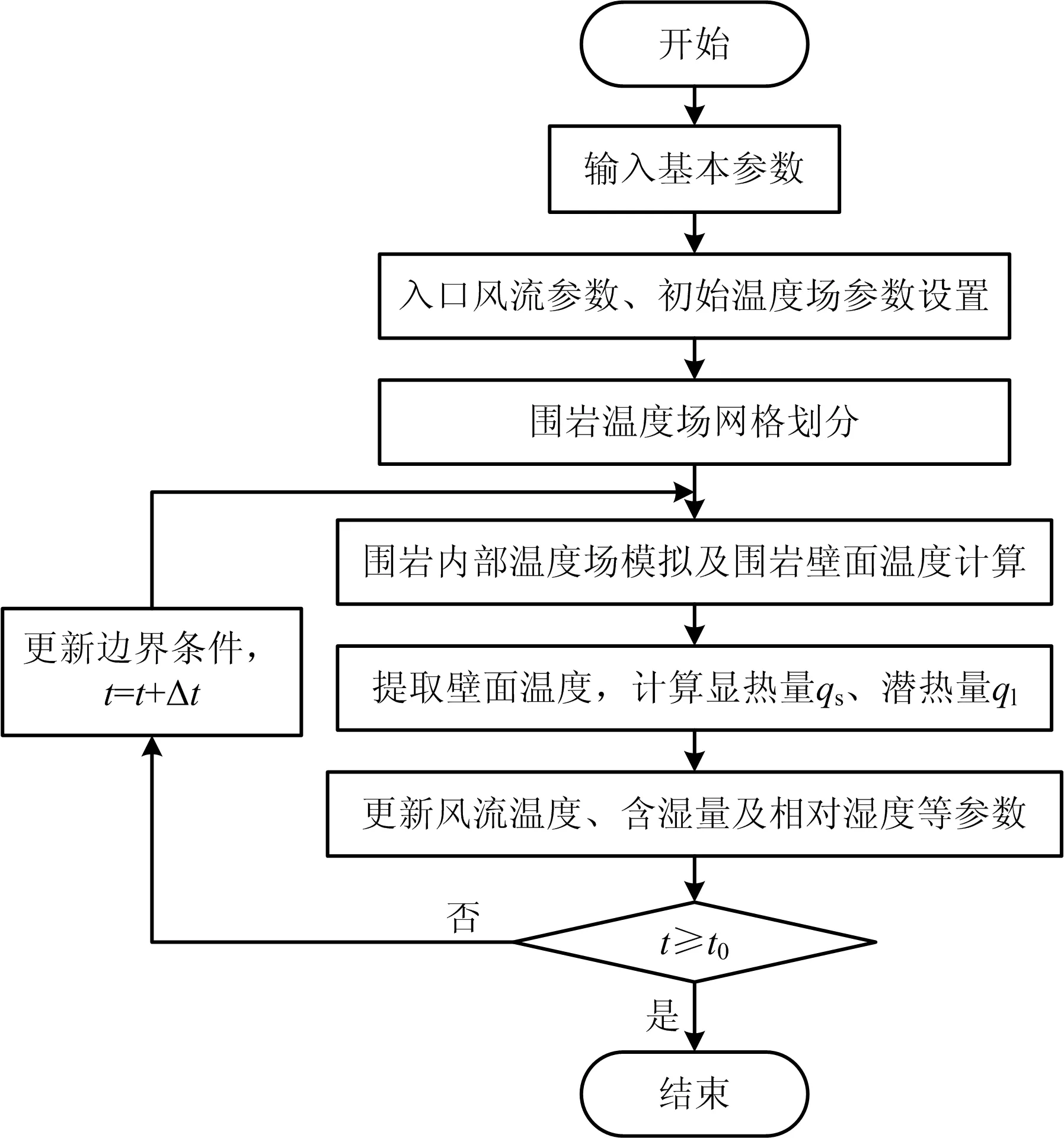
图4 计算流程Fig.4 Calculation flowchart

3 结果分析

结合神东集团大柳塔煤矿52505综采工作面的现场实际情况，利用 C++编写的程序对工作面及进、回风巷内风流温湿度的变化情况进行计算。52505工作面运输巷长度1 265 m，工作面长度300 m，回风巷长度1 265 m，共计2 830 m，作为围岩温度场模拟的轴向长度，后文中巷道轴向位置坐标值x均以运输巷入口为起始坐标点。为避免因边界条件对计算结果产生影响，根据文献中对调热圈的研究，围岩径向温度场深度取为40 m。围岩温度场计算网格为200×20×20。入口风流温度实测为16℃，风流密度为1.2 kg/m3，忽略空气湿度变化对密度的影响，围岩的原始岩温为20℃，岩石的导热系数为13.4 kJ/(m.h.℃)，密度为2 600 kg/m3。巷道等效半径为2.4 m，风量为50 kg/s。

3.1 风流温度变化规律及影响因素分析

风流温度变化曲线如图5所示。结合大柳塔煤矿52505综采工作面的实际情况，从风流温度的计算结果来看，模拟结果与实测结果数值上吻合得较好。

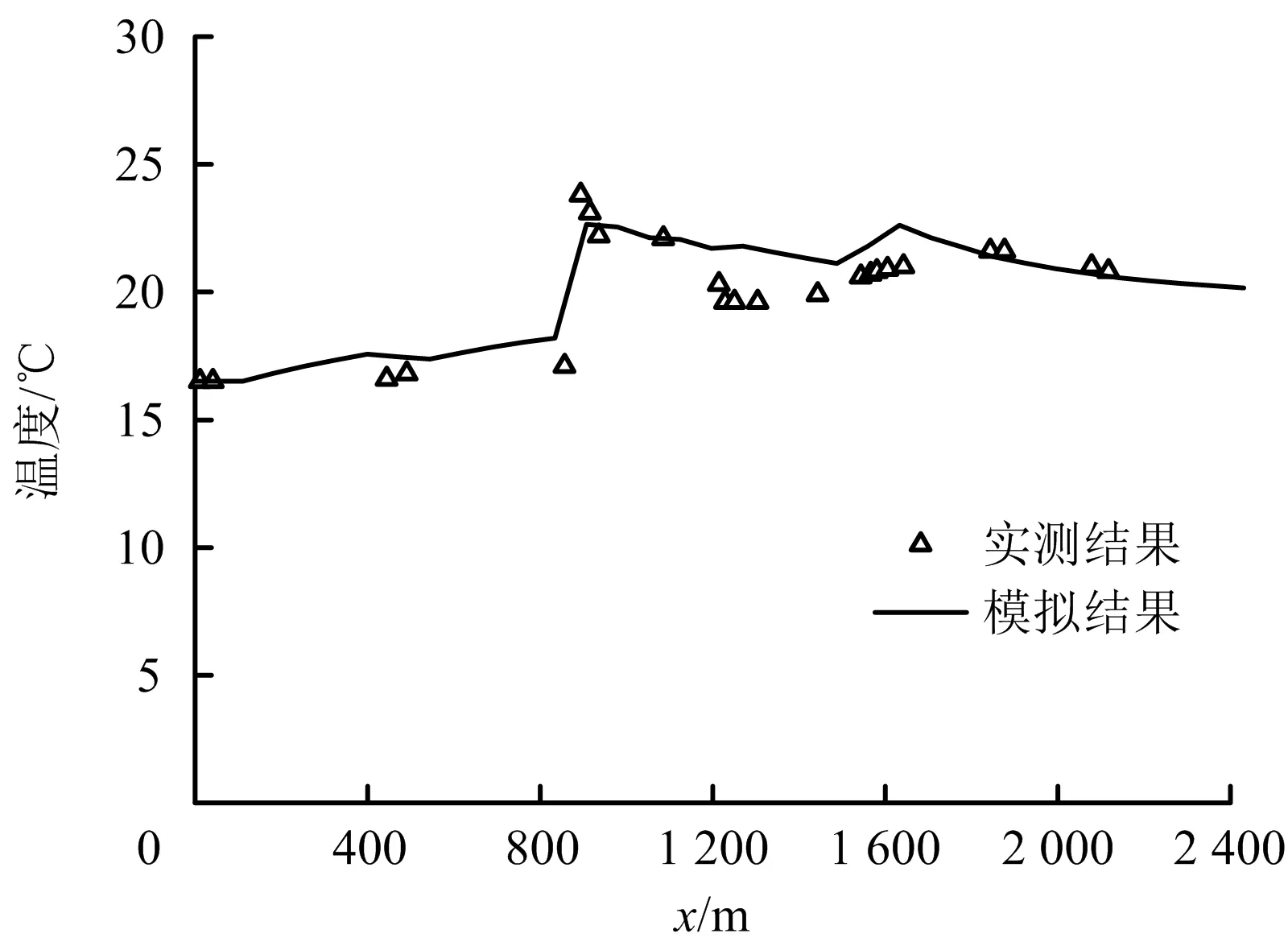
图5 风流温度变化Fig.5 Change curve of airflow’s temperature

在风流刚进入巷道时，由于风流温度变化仅限于与巷道壁面之间的对流换热，且原始岩温较低，因此风流温度变化不明显。但随着风流路径沿巷道的逐渐深入，风流与各种热源设备之间不断地进行换热，使得风流升高。大柳塔煤矿52505综采工作面附近典型热源分布情况如表1所示。在52505运顺16-17联巷、17-18联巷附近热源较多且热源强度较大，因此，在这些位置风流升温较为明显。在此之后风流温度有所下降，这是由于在此处出现了壁面温度低于风流温度而导致的。

表1 大柳塔煤矿52505综采工作面典型热源分布情况Table 1 Distribution of classical heat source of 52505 fully-mechanized face in Daliuta Coal Mine

3.2 风流相对湿度变化规律及影响因素分析

风流相对湿度变化曲线如图6所示。从风流相对湿度的计算结果来看，模拟结果与实测结果数值上吻合得较好。

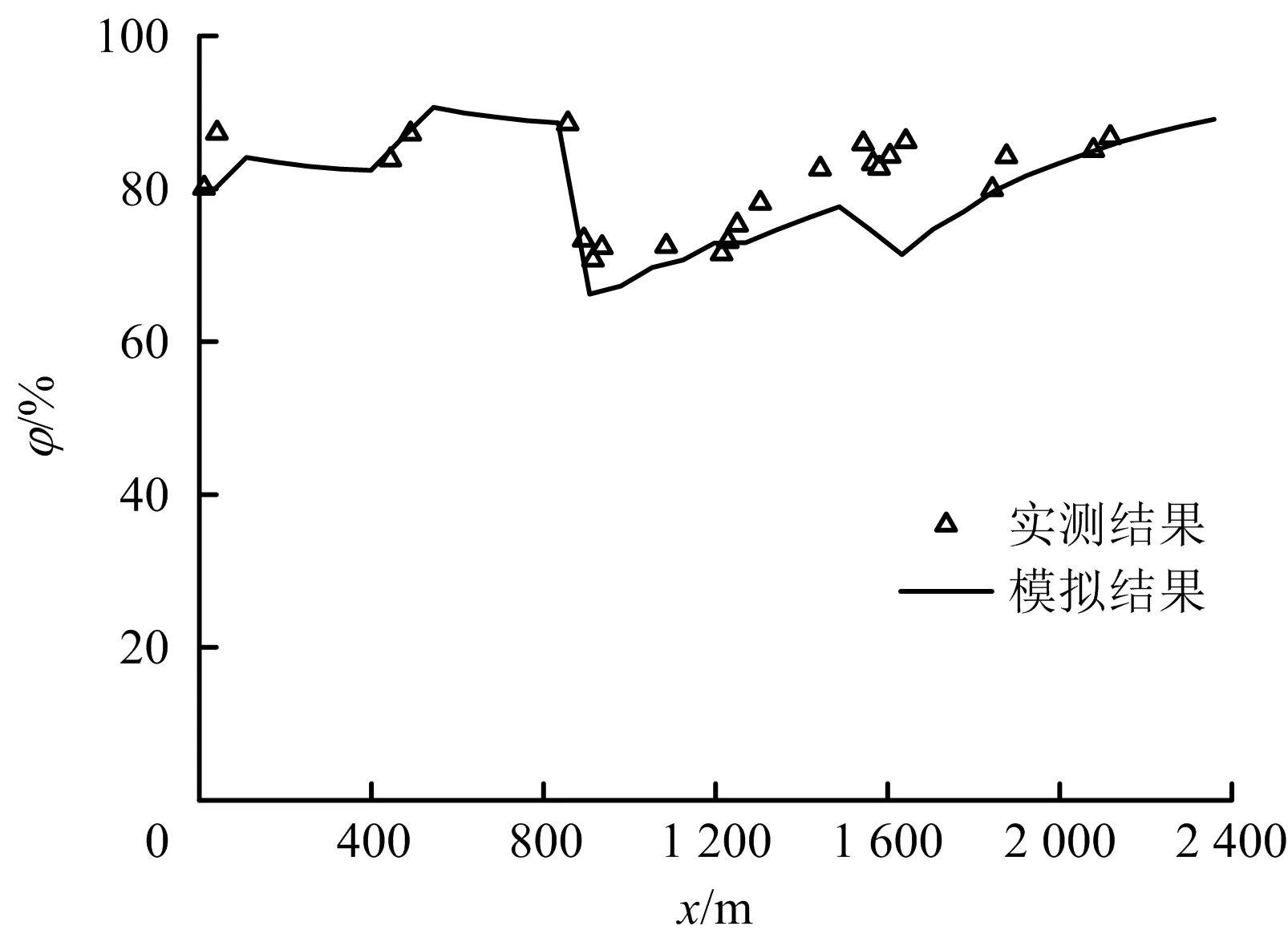
图6 风流相对湿度变化Fig.6 Change curve of airflow’s relative humidity

随着风流的进入，围岩与风流间进行着热湿交换。大柳塔煤矿52505综采工作面附近典型湿源分布情况如表2所示。在52505运输巷部分，散湿地点较多，如52505运输巷2-3联巷水幕上风侧、52505运输巷2-3联巷水幕下风侧、52505运输巷10-11联巷水幕上风侧、52505运输巷10-11联巷水幕下风侧等，导致运输巷中风流湿度较大。而在运输巷的尾部以及工作面，随着热源的增多，风流温度升高，使得相对湿度反而有所下降。

表2 大柳塔煤矿52505综采工作面典型湿源分布情况Table 2 Distribution of classical wet source of 52505 fully-mechanized face in Daliuta Coal Mine

风流温度与壁面温度对比变化如图7所示。从图7中可以看出，围岩壁温的变化要比风温、风流湿度的变化更为复杂，这是由于壁温的变化是壁面与风流之间热交换、壁面与风流之间湿交换以及围岩内部导热之间综合作用的结果。

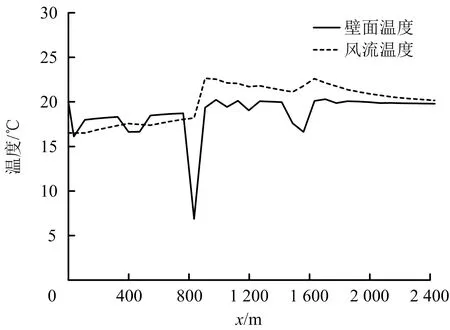
图7 风流温度与壁面温度对比变化Fig.7 Change curve comparison between airflow’s temperature and wall temperature

4 结论

1)充分考虑了壁面水分蒸发以及原始岩温对风流温湿度的影响，建立了数值分析模型，并以大柳塔煤矿52505综采工作面为例，计算得到了与实测参数较为一致的模拟结果，验证了该数值方法的有效性。

2)风流温度受原始岩温、入风流温度、局部热源强度等多方面因素的影响；风流相对湿度与入风流温湿度以及井下湿源的数量和强度有关。

3)巷道壁温作为将围岩温度场与风流参数之间关联起来的主要因素，对模拟结果影响较大，其数值受壁面与风流之间热交换、湿交换的影响，同时还与围岩原始岩温有关。