基于可变模糊集理论的硫化矿炸药自爆危险性评价*

赖 勇，阳富强

(福州大学 环境与资源学院，福建 福州 350116)

0 引言

硫矿资源是社会经济发展中的重要资源，我国已探明硫矿产地1 437多处，储量约58亿t[1]。在硫化矿床进行开采作业时，常利用炸药对矿石进行爆破，但在开采过程中硫化矿石及其氧化产物与炸药接触时会发生放热反应，导致温度过高，发生爆炸事故[2]。随着开采深度的增加，矿井内部的温度不断升高，在用炸药进行爆破作业时，炸药自爆的危险性增加。国内外曾多次发生硫化矿山炸药自爆事故。例如，新疆富蕴蒙库铁矿、内蒙古乌努格土山铜钼矿、广东云浮硫铁矿、巴布亚新几内亚Lihir金矿、美国Meikle金矿等都曾发生过矿石炸药自爆事故[3-5]。因此，开展硫化矿床炸药自爆危险性评价，对减少炸药自爆事故具有重要意义。

目前，硫化矿床炸药自爆的研究较少且主要集中在炸药自爆机理。例如，机械活化理论认为在矿床开采过程中，矿石经各种形式的机械力作用(地压、摩擦力等)，使矿石的物理化学性质发生改变并提高化学反应活性，在一定环境条件下更易发生氧化自热现象[6]。微生物作用机理认为有可氧化硫化矿物的微生物存活于氧化矿带中，在开采过程中微生物在合适的环境下会对矿物进行氧化从而放热[7]。此外，也有学者对硝酸铵的稳定性进行研究，Sun等[8]论证了无机酸对硝酸铵热稳定性的催化效应；Xu等[9]发现亚硝酸钠能够降低乳化炸药的起始分解温度。还有部分学者对炸药自爆危险性进行研究，例如，叶晓晖等[10]利用可拓综合模型对炸药自爆危险性进行评价；罗凯等[11]基于未确知测度模型对硫化矿山炸药自爆危险性提出了新的评价方法；阳富强等[12]利用云模型对硫化矿床开采中炸药自爆危险性进行危险性分析。硫化矿床炸药自爆的研究主要侧重炸药自爆机理研究，对于炸药自爆危险性评价的研究较少，相关的炸药自爆危险性评价研究成果基本上都是用单一模型对样本进行评价，或只能将评价标准处理成点的形式，不能对复杂的井下开采条件进行有效评价。本文将采用可变模糊集理论对影响硫化矿炸药自爆的因素进行分析，利用熵权法确定各影响因素权重，减少主观性。研究结果可为评价高硫矿山炸药自爆危险性提供参考依据，减少矿山炸药自爆事故。

可变模糊集理论由陈守煜在2005年创立[13]，该理论能够有效分析具有模糊性、动态性、不确定性特征的复杂系统[14]。目前该理论主要应用于水利工程、地质灾害等领域[15-17]并已取得成效。由于硫化矿床开采环境复杂，影响炸药自爆的因素具有模糊性和动态性等特点，因此，应用可变模糊集理论对硫化矿床开采中炸药自爆危险性进行评价。

1 炸药自爆危险性可变模糊评价模型

1.1 建立指标体系

对于硫化矿床开采中炸药自爆危险性评价，合理的选择评价指标能够使评价结果更为准确。炸药自爆的危险性与不安全的环境条件、不安全的物质状态以及装药时间有着极为紧密的关系。其中，环境条件主要为矿井内温度、湿度；物质状态主要为矿石自身的物化性质以及炸药的种类。硫化矿床开采中炸药自爆危险性评价的指标选取主要依据过往的自爆事故原因与已有的研究成果，并结合实际的生产情况，经筛选后确定。由于矿井内部环境复杂，在选取指标时应以灵敏性、可变性、易得性及代表性等为原则[14]。

1.2 评价模型与方法

可变模糊评价的具体方法步骤如下：

1)确定样本特征值矩阵

确定待评价样本的指标特征向量x=(x1x2…xm)，其中m为样本指标特征值的个数。

2)确定指标评价区间矩阵

将待评价样本的各指标按照c个级别划分成评价区间，令1级最好，c级最差，区间等级按数字顺序分布，可得到指标评价区间矩阵：

(1)

式中：[aih，bih]为指标i的h级别的标准值区间；aih，bih分别为区间的上下限。

3)根据Iab确定可变范围评价区间矩阵：

(2)

式中：[cih，dih]为指标i的h级别的可变范围值区间；cih，dih分别为区间的上下限。其中[cih，dih]有：

(3)

4)据矩阵Iab，按指标i的物理特性与实际情况，确定指标i级别h的点值矩阵：

(4)

公式(4)中的Mih为：

(5)

式中：h=1,2,…，c。

5)将样本指标特征值xij与Mih比较大小，若xij≤Mih，其隶属函数计算公式为：

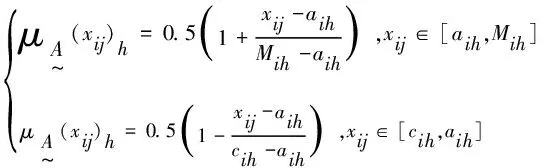
(6)

若xij>Mih，则其隶属函数计算公式为：

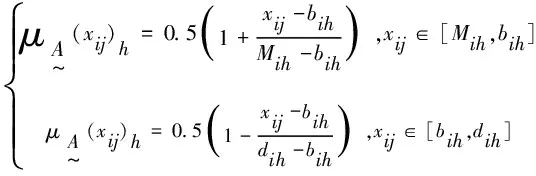
(7)

根据指标特征值xij与Mih，再利用公式(6)、(7)可得相对隶属度矩阵：

(8)

6)确定指标权向量

熵权法是依据各项指标变异程度，利用信息熵的大小来计算各指标权重的1种方法。本文利用熵权法求得炸药自爆影响指标权重w={w1,w2,…,wn}。

7)确定可变模糊综合评价模型

不同参数组合均可得到相应的非归一化综合相对隶属度矩阵，对其进行归一化，可得到归一化的各指标综合相对隶属度值。由公式(9)可得样本对级别h的综合相对隶属度向量：

(9)

式中：wi为指标权重；m为指标数；α为优化标准参数，α=1为最小一乘方准则，α=2为最小二乘方准则；p为距离参数，p=1为海明距离，p=2为欧氏距离。α与p共有4种不同组合。

8)综合评价

由式(10)可得级别特征值H：

Hj=(1,2…c)·uhj

(10)

并结合判断准则：

(11)

根据归属级别Hj的等级对硫化矿床开采中炸药自爆危险性进行评估。

2 实例运用

2.1 评估体系的建立及其样本的特征值

参考有关硫化矿床炸药自爆危险性评价的文献[11]，并结合实际生产情况，选定水溶性铁离子含量、硫化矿石含水量、炸药类型、装药时间等8个影响因素作为评价炸药自爆危险性的综合评价指标，具体指标见表1。根据以往的炸药自爆事故调查报告以及相关的自爆研究，对综合评价指标进行分级与取值[11]。将综合评价指标分为Ⅰ，Ⅱ，Ⅲ和Ⅳ4个级别，依次对应自爆危险性小、自爆危险性一般、自爆危险性大以及自爆危险性极大。其中，炸药类型与装药时间的等级划分与取值是根据炸药的耐热性和实际装药时间与计划装药时间对比决定的。

以某高硫金矿为例，其主要成分为黄铁矿。该矿山的生产事故记录显示，矿山曾发生过自燃事故，未发生过炸药自爆事故。根据炸药自爆危险性评价指标得到矿山的危险评价指标特征值，如表2所示。

表1 炸药自爆危险性评价指标与等级划分Table 1 The risk evaluation indicators and grades of explosive self-explosion

表2 某高硫金矿炸药自爆危险性指标特征值Table 2 The risk indicators characteristic values of self-explosion for a high-sulfur gold mine

2.2 相对隶属度的计算

由表1可得某高硫金矿的炸药自爆危险性的指标评价区间矩阵：

由指标评价区间矩阵Iab和公式(3)可得可变范围评价区间矩阵：

由指标评价区间矩阵Iab和公式(5)可得：

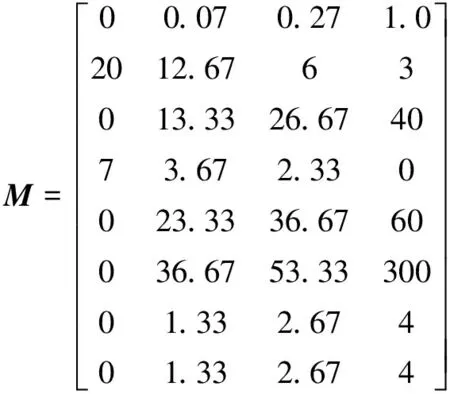
将指标特征值xij与Mih比较大小，然后根据公式(6)、(7)计算出矿山的相对隶属度矩阵：

根据熵权法计算出硫化矿床开采中炸药自爆危险性各评价指标对应的权重值W=(0.127,0.114,0.146,0.243,0.094,0.114,0.081,0.081)。

2.3 硫化矿山炸药自爆综合等级特征值计算

由公式(9)求得α与p共有4种不同组合情况下的未归一化的综合隶属度矩阵，再对其进行归一化处理，得归一化后的综合相对隶属度矩阵。再根据公式(10)、(11)得到级别特征值H，具体数值见表3。

表3 某高硫金矿炸药自爆综合等级特征值Table 3 The comprehensive grade characteristics values of self-explosion for a high-sulfur gold mine

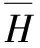
3 结论

1)硫化矿床的实际开采条件复杂，影响炸药自爆的因素多，且各因素间会相互影响。可变模糊集理论对影响炸药自爆指标的范围进行分析，兼顾评价指标所具有的模糊性、动态性，解决了将评价标准处理成点而导致评价结果不准确的问题。

2)根据实际情况选取8项影响炸药自爆危险性的综合评价指标对炸药自爆危险性进行评价。采用熵权法求得各项指标的权重，再利用可变模糊评价模型对矿山的特征值进行计算，得出某高硫金矿的炸药自爆危险性等级为Ⅱ级，自爆危险性一般，计算结果与实际情况一致，表明该方法有效。

3)可变模糊集理论处于不断发展和完善阶段，将该理论应用于实际生产中还有待改进，如可变模糊集理论不能够完全消除模型可变参数取值范围的主观性等。此外，硫化矿床在实际开采中影响炸药自爆的因素尚未被完全理解，需要对炸药自爆机理进行更深入的研究。