混合个数未知的多元正态混合模型的贝叶斯推断
2019-03-05刘鹤飞宗凤喜
刘鹤飞,王 坤,宗凤喜
(曲靖师范学院 数学与统计学院,云南 曲靖 655011)
0 引言
混合模型是一种常见的统计学模型,在工业统计,生物医学统计、经济管理、人工智能等领域都有着非常广泛的应用。张香云和宋红凤[1]研究了基于Gibss抽样的正态混合模型的参数估计。蔡鸣晶[2]研究了正态混合模型的Bayes分析,利用贝叶斯方法对正态混合模型进行参数估计。尤芳[3]研究了EM算法、MCEM算法、Gibbs抽样这三种算法对混合模型参数估计的效果差异。但是以上的方法都是在混合个数明确已知的情形下,直接对模型中的未知参数进行估计。Richardson[4]研究了混合个数未知时有限正态混合模型的模型选择的问题,利用可逆跳MCMC算法计算混合个数的后验概率,选出后验概率最大的那个作为模型的混合个数。
本文在已有研究的基础上,将观测变量从一维扩展到了多维,研究混合个数未知的多元正态混合模型。先采用可逆跳MCMC算法对模型中未知的混合个数进行选择,然后在混合个数确定的情形下,用传统的MCMC算法对混合模型中的未知参数进行贝叶斯估计。
其中,在利用可逆跳MCMC算法时,需要对模型中所有的待估参数进行分裂与合并,而对于多维观测变量来说,还要求协方差矩阵都必须是正定矩阵,即利用可逆跳MCMC算法分裂与合并协方差矩阵时,要保证每一个协方差矩阵Σ都是正定矩阵,这是一维观测变量模型使用可逆跳MCMC算法时所不曾遇到的问题。
1 模型描述
假设yip是模型的观测变量,其中i=1,2,3…,N是观测对象,P是多元正态分布的维数。则多元正态混合模型的定义为:

其中,yi是观测向量,且y1,y2,…,yN相互独立,K是模型的混合个数,表示模型是由K个独立的多维正态分布混合而成,θj就是第j个混合部分的正态分布的参数,即θj=(μj,Σj)。wj是第j个混合部分的权重,0 为了研究的方便,本文定义一个隐状态Zi,其中: 当隐状态Z给定的条件下,观测向量来自于与其状态对应的多元正态分布,即: 上式就是K个混合部分的多元正态混合模型的数学定义。 将模型中的观测变量记为Y,隐状态向量集合记为Z,权重向量记为W,多元正态分布的参数(μ,Σ)记为θ,则该模型的贝叶斯推断问题为相应的MCMC算法的具体执行步骤为: 步骤1:更新隐状态Z; 步骤2:更新权重W; 步骤3:更新多维正态分布的参数θ; 步骤4:将一个混合成分分裂成两个混合成分或者将两个混合成分合并成一个混合成分。 步骤1至步骤3是传统的MCMC算法,使用Gibbs抽样和MH算法即可,其中步骤3更新多维正态分布的参数θ又可以分解为两小步,更新多元正态分布的均值向量μ和更新多元正态分布的协方差矩阵Σ,步骤4是可逆跳步,这一步是进行模型选择的关键,在这一步中,可能增加一个混合成分或者减少一个混合成分,并以一定的概率接受这种改变。 贝叶斯学派最基本的一个观点是,任何一个未知参数θ都可以看作一个随机变量,应该用一个概率分布去刻画θ的未知状态,这个概率分布通常被称为未知参数的先验分布[5]。本文参考已有文献的选取经验,为模型中的各个参数选择的先验分布为: 其中,α是狄尼克雷分布D中的超参数;μ0j是第j个多维正态分布的先验分布均值,Λ0j是第j个多维正态分布的均值的先验协方差矩阵,μ0j和Λ0j都是超参数;Wishartp表示P维的威希尔分布,R0j和ρ0j是威希尔分布中的两个超参数。在本文的研究中,混合个数也是未知的,在贝叶斯推断中也应该看成是一个未知参数,在这里选择离散的均匀分布作为该参数的先验分布。 1995年,Green[6]提出了可逆跳跃MCMC方法,该方法通过在可变维参数空间中跳跃式抽样,实现模型选择的目的。1997年,Richardson和Green[4]正是利用这种可逆跳MCMC方法,对于正态混合模型中未知的混合个数进行选择。本文就是在此基础上,将一元正态混合模型扩展到多元正态混合模型,以增加一个混合部分为例,该算法的具体执行过程描述如下: (1)从当前的K个混合部分中等概率随机的挑选一个; (2)从事先给定的分布中抽取一个随机数向量; (3)利用所抽取的随机数向量,将选中的混合部分的参数分裂成两个混合部分; (4)以概率min(1 ,A)接受这个跳跃,其中: A=似然比×跳跃比×先验比×建议比×雅克比 假设当前的混合个数为K,则对于P维观测变量的多维正态混合模型来说,此时的权重向量是K维的,并且有K个P维的均值向量μ,有K个P维正定的协方差矩阵Σ。根据可逆跳MCMC算法的原理,参数分裂之后,K维的权重向量变成K+1维的,且增加一个P维均值向量μ和一个P维的协方差矩阵Σ,并且协方差矩阵必须是正定矩阵。 将选中的待分裂的混合部分标记为j*,将j*分裂后的两个混合部分分别标记为j1,j2。则生成随机数分裂权重W的方式为: 生成随机数分裂均值向量μ的方式为: 生成随机数分裂协方差矩阵Σ的方式非常特殊,根据可逆跳MCMC算法参数分裂原理的要求,需要保证分裂和合并的过程是可逆的,即分裂和合并的过程要一一对应而且能完全覆盖整个参数空间,另外,还要保证协方差矩阵Σ是正定矩阵这个特殊的要求。所以,协方差矩阵Σ的分裂和合并也是将一元正态混合模型的可逆跳MCMC扩展到多维正态混合模型的可逆跳MCMC时的困难之处。本文根据正定矩阵的Cholesky分裂原理,提出了一种分裂和合并的方法,符合以上所有的条件,。 因为正定矩阵都是对称矩阵,所以P维协方差矩阵Σ中有个自由元素。根据正定矩阵的分裂原理,从标准正态分布中生成/2个随机数,将这些随机数按次序排列成一个标准的下三角矩阵L,对协方差矩阵Φj*进行分裂的时候,令Φj1=Φj*,Φj2=L∙LT即可。对协方差矩阵Φj1和Φj2进行合并的时候,令Φj*=Φj1,然后对Φj2进行Cholesky分裂,就可以得到相应的随机数,这个分裂和合并的方法是可逆的,而且理论上能取到参数空间的所有值,更重要的是可以保证分裂和合并的过程中每一个协方差矩阵都是正定矩阵。 对本文来说,贝叶斯后验即P(Z,W,θ|Y),尤其是对模型中的未知参数W和θ进行估计,其中θ包括均值向量μ和协方差矩阵Σ。由于这个后验分布非常的复杂,本文采用MCMC方法来对后验分布进行后验模拟,下面来推导后验模拟时需要用到的满条件后验分布: 因为: f是在第j个混合部分的参数(μj,Σj) 下,观测向量yi的似然函数。 由于各混合部分的权重只与观测变量的隐状态的取值有关,所以: 又因为权重向量W的共轭先验分布是对称的狄尼克雷分布所以权重向量W的满条件后验分布[7]为: 其中,nj是隐状态为j的观测变量的个数。 进一步,推导多元正态分布均值向量μ的满条件后验分布P(μ|Y,Z,W,Σ),因为一旦所有观测变量的隐状态确定的话,权重向量W即可随之确定。此时第j个多维正态分布的均值向量μj只与观测变量Yj及协方差矩阵Σj有关,也即其中,Yj是隐状态取值为j的观测变量的集合,Σj是第j个多维正态分布的协方差矩阵。 因为多维正态分布N(μ,Σ)的联合概率密度函数为: 由于μj的共轭先验分布为N(μ0j,Λ0j) ,其中μ0j和Λ0j是超参数,都可以看成是已知的,所以μj的后验密度的形式为: 忽略上式中的常数因子,将其简化为: 这表明,μ的后验密度仍然是P维正态分布,所以为均值向量μ选择共轭多元正态分布是合理的,且μk后验均值向量协μjp协方差矩阵Λjp分别为: 也即,μj的满条件后验分布[8]为: 其中,nj是观测变量中隐状态为j的总个数是隐状态为j的所有观测向量的均值向量。 最后来推导多维正态分布N(μj,Σj) 的协方差阵∑j的满条件后验分布[9]。 ∑j的先验分布是一个威希尔分布Wishartp(R0j,ρ0j) ,其概率密度函数为: 记Yj为隐状态为j的观测变量的集合,则Σj的满条件后验分布的密度函数有以下形式: 上式表明,Σj的满条件后验分布为: 其中,nj是隐状态为j的观测变量的总个数,IWp表示P阶的倒威希尔分布。 上面推导出了所有未知参数的满条件后验分布,但是在混合模型的研究中,还有一个非常重要的问题就是标签转换。因为如果不处理好标签转换问题,在迭代的过程中,不同的混合部分就有可能发生混乱,肯定会影响估计的结果。交换抽样技术[10]是现在最常见的解决混合模型标签转换的方法之一,但是也有很多文献是通过对模型中某个特定的参数进行控制来解决标签转换这个问题的。比如,Richardson和Green[4]通过限制均值μ1<μ2<…<μn来解决就是一个非常好的例子。本文为了防止不同混合部分下的多维正态分布的参数在迭代的过程中发生混乱,采用限制均值向量的第一维分量的大小的方法来解决这一问题。在每一次迭代更新参数之后,比较μ1,1,μ2,1,…,μk,1的值,如果μ1,1<μ2,1<…<μk,1,则进行下一轮的迭代更新,否则按照不同混合部分均值向量的第一维分量从小到大的顺序重新排序,并且重新分配隐状态的标签值,然后再进行下一轮的迭代。通过这种方法就可以保证在迭代的过程中不同隐状态下的参数不会发生混乱。 在真实的模型中,本文取混合个数K=2,观测对象的个数N=500,多元正态分布的维数P=2,两个多元正态分布的权重分别为0.5和0.5,两个多元正态分布N(μ,Σ)的均值向量和协方差矩阵分别为 取狄尼克来分布中的超参数α=1,多元正态分布均值向量中的超参数为2阶单位矩阵,j=1,2;威希尔分布中的超参数ρ0j=6,j=1,2;R0j=I,I为2阶单位矩阵,j=1,2。 利用可逆跳MCMC算法选择模型中的未知混合个数时,迭代的总次数为5万次,删去前面的3万次,用后面的2万次的迭代结果来计算未知混合个数K的后验概率,图1是混合个数的迭代路径图,表1是混合个数的后验结果。 图1 隐状态个数的迭代路径图 表1 隐状态个数的后验结果 根据表1混合个数K的后验概率,本文选择模型的混合个数为2,接下来再用马尔科夫链蒙特卡罗算法对混合个数确定时模型中的所有参数进行贝叶斯估计,超参数的取值不变,取MCMC算法的迭代次数为1万,去掉前面的5千次,用后面5千次迭代的后验均值作为参数的估计值,估计结果见表2。 表2 各参数的MCMC迭代真值和估计值结果 本文研究了混合个数未知的多元正态混合模型后的贝叶斯推断,利用可逆跳MCMC算法对未知的混合个数进行了贝叶斯模型选择,给出了算法的具体执行步骤,在分裂和合并多元正态分布的协方差矩阵Σ时,除了要满足可逆跳跃算法的要求,还必须保证分裂和合并过程中每一个协方差矩阵都必须是正定矩阵,本文根据正定矩阵的Cholesky分裂原理,提出了一种符合以上所有要求的协方差矩阵的分裂和合并的方法,这种方法可以推广到其他多维分布协方差矩阵的分裂和合并中去。 确定出模型真实的混合个数以后,即当混合个数已经确定时,利用MCMC算法对模型的其他未知参数进行了贝叶斯估计,将表2中的各未知参数的估计值与事先确定的模型的真实值进行对比,显示该方法的估计效果比较好。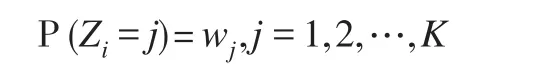

2 贝叶斯推断原理
3 先验分布

4 可逆跳跃MCMC过程


5 后验推断


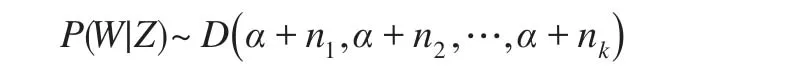









6 数值模拟



7 结论
