基于FAHP-CEEMDAN的指标权重确定方法
2019-03-05张振刚
张振刚,盛 勇,欧 晨
(华南理工大学 工商管理学院,广州 510641)
0 引言
在综合评价方法中,指标权重反映了决策者对某一对象不同属性的综合度量,在评价结果的科学合理性与否起着至关重要的作用。自从1970年Saaty[1]提出AHP(层次分析法)以来,该方法在综合评价指标权重确定中得到了广泛认可与应用。随后,为了表达决策者模糊偏好,Buckley[2]引入模糊理论中的模糊数来表示两两指标间的重要程度,首次提出了FAHP。随着模糊理论的发展,目前较为常用的模糊数有三角模糊数、梯形模糊数与直觉模糊数及区间直觉模糊数等[3-5]。而相比于精确数判断矩阵,这些模糊数判断矩阵的解法也相对复杂。L.Mikhailov[6]提出了FPP模型并采用线性规划的方法来求解判断矩阵。S Bodjanova,X Liu等[7,8]采用去模糊化的思想得到特殊点,然后根据这些特殊点构造精确判断矩阵求取权重。针对零权重以及判断矩阵内在不一致并可能产生多解的问题,Wang,Y.-M.[9]提出了LFPP模型。以上方法,均是针对单个或者少数专家的判断矩阵的解法。
随着社会的不断进步,经济社会活动中的决策问题变得日益复杂,仅仅依靠单个或少数决策者做出有效的决策越来越困难[10]。为了保证评价的客观性,需要邀请多位专家对指标的重要性进行评估并确定权重,从而形成了群决策。目前群决策问题引起了广泛的关注,而对多位专家给出的重要性评估如何进行集结是一个研究热点。当前集结的方式大概可以分为两类:一是通过某种方法将专家的判断矩阵进行集结后再处理该综合集结矩阵[11-13];二是先处理各个专家的判断矩阵,然后再进行综合集结[14-16]。由于不同专家意见具有较大的主观性、模糊性以及差异性,影响最终决策的指标非常复杂,不同专家的模糊决策信息提取也较为困难。再者,目前的研究大都是构建各个专家的判断矩阵,若专家数量过多,再对其进行建模计算集结会十分复杂和困难[17]。
针对以上问题,本文采取后一类集结方式的思想,重点研究了FAHP与去除主观任意性的权重获取与优化策略——改进集合经验模态分解(CEEMDAN)方法,视各个专家评价值为一系列非平稳信号,利用信号分解提取技术,提取专家评价值中的客观趋势信息,去除随机扰动主观判断信息来优化评价值并求取最终指标权重值。
1 改进集合经验模态分解(CEEMDAN)
改进集合经验模态分解是由法国学者Colominas等[18]提出,针对非平稳信号将其分解为各个本征模函数(IMF)之和的一种信号处理方法。该方法无需设定拟合基函数,可根据数据自身的尺度特征来进行分解,适用于各种类型的信号分解。相比于传统的EMD(经验模态分解),CEEMDAN在分解的每一阶段添加自适应的白噪声,计算唯一的残余信号,从而能更有效避免模态混叠效应、端点效应,提高信息序列分解的准确度。目前,该方法是提取信号以及均值趋势非常有效的一种方法,已广泛应用于天文测绘、地震预测、机械诊断与金融时间序列分析等。CEEMDAN的具体操作步骤如下:

步骤2:向分解后的r1(t)信息序列中继续添加m次高斯白噪声并分别运用EMD进行分解,进而求取第2个IMF分量均值。设Ej(·)为经过EMD分解后的第j个IMF分量,则信息序列
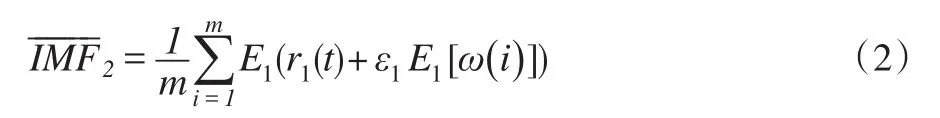
步骤3:对于k=2,3,…,n,类比上述求解方式,计算第k个残余分量如下:的第2个IMF分量为:

步骤4:重复步骤2,分解直至平均包络线为零,得到第k+1个IMF分量:
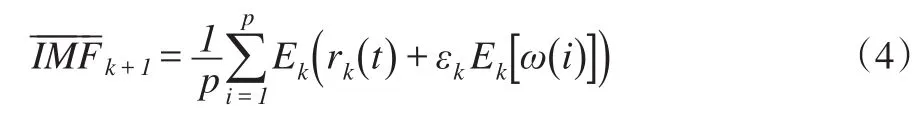
步骤5:重复以上步骤,直到不能从中提取满足IMF条件分量[19]时,循环结束,最终的余量信号为:

式中,rn为残余函数,代表信息序列的平均走向趋势。分解过程中,通常m取102数量级,εi取10-2数量级。
2 模糊层次分析法
模糊层次分析法的基本思路是采用“模糊矩阵”替代AHP中的专家“判断矩阵”。模糊矩阵的构造有多种方法,其中最常见的是用三角模糊数代替精确数来表示判断的模糊性。实践证明,使用“三角模糊数”语言变量带有模糊性的方案能得到比较满意的结果。
2.1 三角模糊数
三角模糊数=(l,u,m)根据其隶属度函数可定义为:
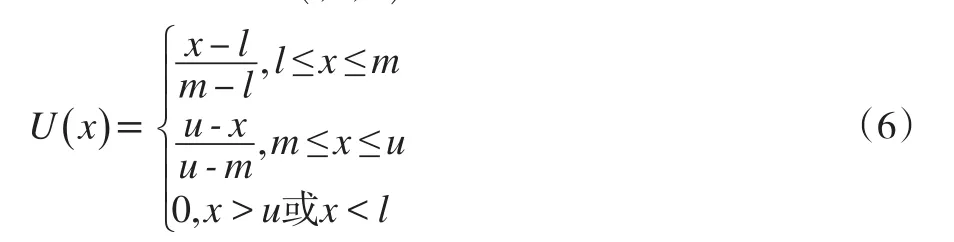
式中,m是三角模糊数的中值,l与m分别为相应的左端点和右端点。
2.2 三角模糊数标度的研究
在实际中,由于大多数语言表达通常具有一定的模糊性,运用三角模糊数来表达这种模糊性。表1给出了不同的互反三角模糊数评估标度:

表1 三角模糊数标度比较
文献[20]将传统的层次分析法标度拓展到模糊数,文献[21]与之相对应扩大了模糊数范围。对于一个指标相比于另一个指标重要程度势均重要(不相上下)时,三角模糊数与其互反矩阵是等同的(1/2,1,2)。这样,专家在给出判断矩阵时便能很好地体现两指标对比不相上下的模糊情况(而并非完全等同)。因而,本文采用文献[21]的三角模糊数。
2.3 基于LFPP模型的单模糊层次分析法
由于传统的模糊层次分析法存在负隶属度函数产生无效解、判断矩阵的不一致性会造成多解以及上三角与下三角元素不同会产生不同的优先权重向量等缺陷,Wang和Chin[9]提出了基于LFPP模型的单模糊层次分析法。目前,该方法已广泛应用于决策方案选择与综合评价中,并取得了良好的效果。
运用单模糊层次分析法作指标间的两两比较判断时,采用模糊数来表示一个指标相比于另一个指标的重要程度。设为一指标集,根据表1中改进的三角模糊数,则表示各指标两两比较的模糊互反判断矩阵为:
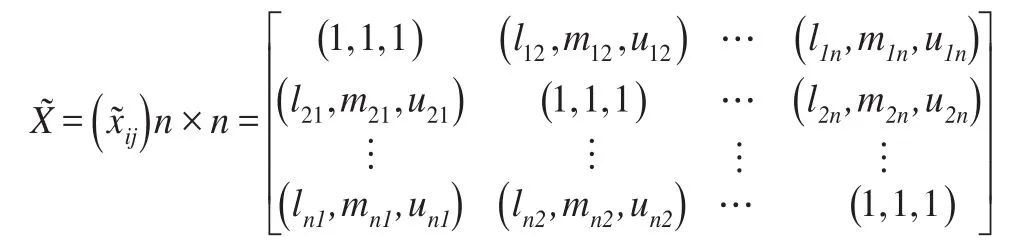
其中,对于任意的i,j=1,2,…,n且i≠j,应满足:

将以上互反模糊判断矩阵取对数,可得到以下方程:

于是隶属度函数式(1)可改写为以下形式:隶属于三角模矩阵


其中δij与εij表示满足约束条件的偏差变量,ωi为专家对指标i的评价值,M是一个充分大的常数(为得到最优λ,通常取M=1011)[22]。另外,这里需满足否则重新返还专家进行矩阵一致性修正。这样,便可以求解单个专家的判断矩阵得到各个指标的评价值。
3 基于FAHP-CEEMDAN的指标权重确定方法
3.1 专家指标评价值的组成分析
在实际的评价过程中,通常所筛选的专家是熟悉该领域并且水平相差不大的专家,不过每位专家所处的社会环境、个人经验不同[23],可能给出不同程度的判断矩阵。由此,根据模糊层次分析法计算得出的指标评价值可能是一系列不规则、并非平稳的数值序列。在相当程度上,可以将其视为非平稳信息序列,进行信号提取处理,从而获得信息序列的平稳客观趋势信息。采用CEEMDAN法对处理各专家的评价值和最终集成结果如图1所示:
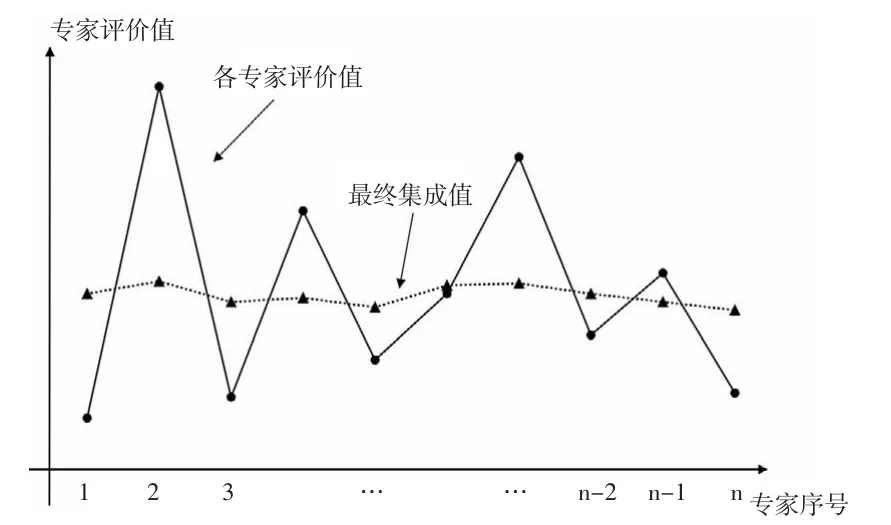
图1 专家评价集成值
图1中,圆点为专家的评价值(采用折线相连),三角形则表示最终集成结果。不难看出,各专家的评价值围绕着最终集成值上下波动。这表明在消除各个专家的主观个人偏好与偏差评价值以后,各专家对待评价指标的客观值往往趋近于一条波动不大的平稳曲线(图1虚线)。因此,可以这样推断:群体的最终一致评价值便是去除主观个人偏好及评价偏差后的最终结果。换句话说,即去除一致评价值,各个专家评价值所剩下的残余量反映着专家的主观偏好与主观判断偏差,是一系列无规则混乱的点。
因此,可认为专家的评价值包含两部分成分:主观判断成分与客观趋势成分。主观判断成分即主观个人偏好与偏差评价值,而客观趋势成分即是专家群体最终一致趋势评价值。
3.2 基于FAHP-CEEMDAN的指标权重确定策略
假设C={C1,C1,…,Cm}为待评估指标集,有q={E1,E2,…,Eq}位专家采用1.2节的标度对m个指标进行两两对比给出各自的判断矩阵,试确定各个指标的权重。下面给出具体的求解步骤:
步骤1:根据1.3节的单模糊层次分析法,计算得出q位专家对于指标Ci(i=1,2,…,m)的评价值:

步骤:2:将信息序列ω(Ci)序列加入m=100次高斯白噪声并形成的m组新序列分别进行EMD分解并求取IMF分量均值,得到第1个均值分量,此分量代表专家对指标Ci的评价值中受主观判断因素影响最大的低频成分。
步骤3:向步骤2中分解出的残余分量ri1(t)继续添加白噪声分别进行分解,并求取IMF分量均值,得到第2个均值分量,此分量代表专家对指标C的评价值中i受主观判断因素影响次大的低频成分。
步骤4:重复步骤2和步骤3多次,直到不能从中提取满足IMF条件分量[19]时,循环结束,此时rin(t)(t=1,2,…,q)信息序列就代表了专家对指标Ci评价值中的客观趋势成分。
步骤5:同理,分别求取m个指标Ci(i=1,2,…,m)的残余分量信息序列rt(Ci)(i=1,2,…,m)。
4 实例分析
在科技机构改革中,需要对科学研究与技术开发机构进行调研分析,确定科学研究开发机构的创新能力评价指标权重。调研组综合制定了4个一级评价指标:创新投入能力(C1),创新管理能力(C2),创新产出能力(C3)和创新社会效应(C4)。现邀请了15位该领域的专家进行综合评价以确定各个指标的权重。
(1)将现有15位专家进行编号{E1,E2,…,E15}。专家采用1.2节的改进标度给出了各自的模糊判断矩阵(见表2)。限于篇幅,本文只列出专家E1的判断矩阵,其他专家的判断矩阵不一一列出。

表2 专家E1给出的模糊判断矩阵
(2)根据1.3节的模型,令M=1011,采用Excel建模规划求解得到专家E1对各个指标的评价值为ω1=2.713,ω2=2.517,ω3=3.618,ω4=1.602(未标准化),λ=0.041其他专家采用相同解法,结果如表3所示:
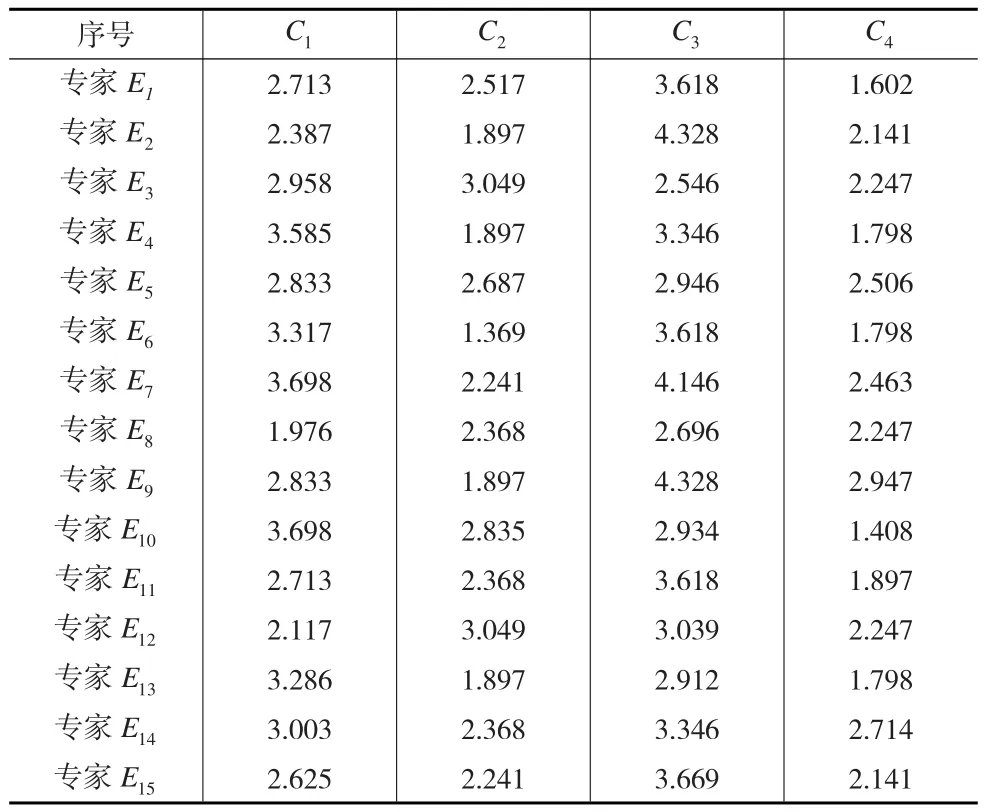
表3 采用LFPP-FAHP所得4个指标评价值
(3)利用R语言编程CEEMDAN分解模型,分别分解各个专家的评价信息,得到残余分量和IMF分量图如图2:

图2 C1至C4评价值分解比较
图中实点代表分解前的专家评价值,空心圆点代表CEEMDAN分解后已达阀值条件[17)]的分量之和,即由专家矩阵获得的评价值的主观判断成分。空心圆点代表分解后的残差量,即专家评价值的客观趋势成分。由于去除IMF分量后的残差量的趋势变动较为缓慢趋于一条平稳曲线,可认为随机波动成分(主观成分)已经大致消除。因此,可以认为各专家真实客观的评价值即是该一系列空心圆点。
(4)因空心圆点已基本消除专家评价值的主观成分,并缓慢趋近于一条波动很小的平稳曲线,同时在同领域专家水平相差不大的情况下,已无需再通过求取专家权重的方式集成客观趋势成分。最后,采用第3.2节几何均值法即可获得专家群体对各个指标的客观趋势权重
5 结论
针对不同专家判断矩阵确定权重的模糊性较大以及主观意见不统一的问题,本文提出了一种基于FAHP-CEEMDAN的新的权重确定方法。该方法将FAHP与CEEMDAN二者有机结合起来:前者确定专家模糊判断矩阵并优化获取指标的评分值,后者采用信号处理技术,提取多名专家权重的客观趋势成分,最后采用该成分的几何均值作为最终权重结果。与其他方法相比,该集成专家评价值的方法能更好地排除专家主观判断的成分,保留客观趋势成分,从而反映出待评对象的真实客观情况;其次是该方法还可以运用于大规模群体决策以及群体判断信息客观趋势的把握。本文提出的方法可以有效解决现实生活中的评价指标权重确定问题,进一步丰富和发展了群决策求取权重的方法。最终权重结果会受到专家数量关系一定程度的影响。
