能值型综合能效指数编制的构想
2019-03-05胡萌
胡 萌
(青岛大学 经济学院,山东 青岛 266071)
0 引言
节能减排是我国的基本国策,是可持续发展的要义之一。研究经济系统对能源系统的利用水平是能源经济学和能源统计学的重要课题之一。对这一问题的研究先后出现过两个概念,一是能源利用效益,二是能源利用效率,目前,两个概念被混淆并更多地使用后者。李为正(1984)[1]就明确区分了两者:能源利用效益是能源利用过程中所产生的经济效果与被使用的能源量之比。能源利用效率是能源利用过程中被有效利用的能源量与被使用的全部能源量之比,是一个没有量纲的相对数,与物理学上的“效率”概念基本相同,Patterson(1996)[2]也称其为热力学能源效率,而将能源利用效益称为经济学能源效率。显然,能源利用效率是单纯的能源系统内的概念,它是一个热效力概念,投入和产出都以热值单位来衡量。能源利用效益才是能源系统和经济系统相结合的概念,可以描述能源系统的投入与经济系统的产出之比,前者以投入能源的热值单位表示,后者以产出(产品或服务)的数量或产值来表示。特定总体内各种产出的能源利用效益的综合称为综合能源利用效益,如今被广泛使用的单位GDP能耗、单位工业增加值能耗等指标(经常也被称为能源强度)都属于反映综合能源利用效益的指标,且是价值型指标。基于这些指标展开的相关研究也形成了持续且丰富的成果,其中一类是关于能源强度的变动(能源强度指数)及其因素分解的研究,历年被引用次数较高的研究成果包括但不局限于文献[3-10]的研究。上述能源强度指数的优点是数据需要量少,编制简单,但是在真实地反映综合能源利用效益(以下简称能效)及其变动上还存在重要缺陷。本文以统计指数理论为分析框架,探讨一种新型的综合能效指数——能值型综合能效指数的编制构想,并基于它建立因素分解分析的构架,以期更为科学地反映综合能效随时间的变动和在空间上的差异。
1 个体能效指标和个体能效指数
要研究综合能效指标和指数,先要分析个体能效指标和指数。按照本文对能效的定义,个体能效是单个产出的能效,它是生产一单位产品或服务所需投入的能源数量,即单位产品能耗,简称单耗。个体能效指数则是个体能效指标的变动,即单耗的变动,表示为:
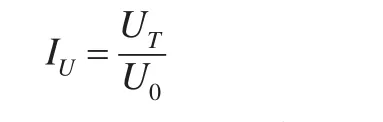
其中,IU为个体能效指数,U为产品单耗,T为报告期或对比主体,0为基期或参照主体。
对于单耗指标,其分母应使用实物量单位而非价值单位,依实际需求的特性不同,产出的实物量可采用不同单位,如重量、面积、长度等,因为使用价值单位会受到价格变动的影响。例如:某年生产1吨焦炭消耗250千克标准煤,如果明年这个数字为230千克,就可以说焦炭的能效提升了。如果某年生产1千元焦炭消耗250千克标准煤,而明年焦炭价格上升20%,则生产1千元焦炭只需消耗208千克标准煤,显然,焦炭单耗的下降是价格上升导致,并非其能效的上升,生产1吨焦炭消耗的能源数量并无下降。因此,个体能效指标中的产出使用实物量单位,能够反映为生产一定数量的实际产出而非名义产出所消耗的能源数量。一个特定总体,比如一个企业、一个行业、一个产业、一个地区等的能源利用效益,应是指其生产的各种产出的单耗的综合值,称为综合单耗或综合能效。因此应以该值来比较不同总体的能效的空间差异和同一总体的能效的时间差异,这就需编制综合单耗或综合能效指标,继而计算综合能效指数以反映总体中多种产品单耗的综合变动。
2 价值型综合能效指数及其存在的问题
徐国祥(2011)[11]认为统计指数理论对于总体对象的研究采取的是自下而上的思路,即通过同度量因素将总体中的各经济变量转换成可以加总的总量指标,然后以总量指标对比所得到的相对数来说明总体这个复杂现象量的综合变动。在将个体能效指标加总的过程中,价值型综合能效指标引入的同度量因素是价格,它是当前普遍使用的一种综合能效指标,一般有两种形式,一是总产值综合能效指标;二是增加值综合能效指标,相应地也形成这两种指数。总产值综合能效指数的计算公式为:
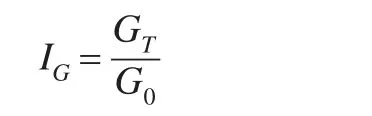
其中,G为价值型综合能效指标,即单位总产值能耗,其计算公式为:
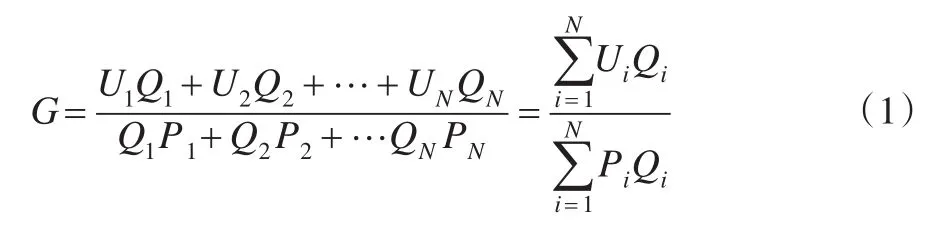
式中:U、Q、P分别为产品单耗、产品数量和产品单价,N为产品种类。
总产值综合能效指标的统计意义明确,它以价格为同度量因素,反映了产品篮子的总能耗与产品总价值之比,因此,从指标构造的逻辑来说比增加值综合能效指标(单位增加值能耗)更清晰,增加值综合能效指标实际上是其衍生指标,两类指标之间存在着一定的数量关系。即:

可见,总产值综合能效相同的情况下,增加值率越高,增加值综合能效指标值越低。利用价值型综合能效指数反映能效的综合变动存在诸多问题,不能真实地反应综合单耗的变动,主要体现在:
2.1 价值型综合能效指标的分母计算存在问题
两种价值型综合能效指标的分母都是价值量。总产值型综合能效指标的价值量是总产值,存在重复计算,不能反映某一特定产品的生产过程对应的能效水平,与分子的计算口径不一致。比如,计算钢铁制造业的总产值综合能效指标,分母是钢铁制造业的总产值,其中至少包含了铁矿石采掘业的总产值,因此,价值量(分母)对应的是铁矿石和钢铁制造两个生产过程,而能耗(分子)对应的是钢铁制造过程,分子和分母的计算口径是不一致的。此外,总产值的大小与重复计算程度有关。比如,工业总产值的重复计算程度取决于生产的分工程度,分工越深化,重复计算越多,总产值能效指标值就越低。因此,如果比较两个地区的总产值能效,指标值低的地区并不一定代表其能效水平高,可能是其分工程度比较细,导致总产值重复计算程度高,而使得产值能耗指标值低。增加值综合能效指标则避免了上述口径不一致和重复计算的问题,但是该指标没有依照统计指标的原理进行构造,且中间消耗匹配的正确性会影响到指标的计算结果。
2.2 价值型综合能效指数易受价格和产品结构影响
鉴于增加值综合能效指数是总产值综合能效指数的衍生形式,以下以总产值综合能效指数为例进行分析。根据公式(1),以价格作为同度量因素,价格高的产品对综合能效指标的影响大。分子,即总能耗一定的情况下,单位价格越高,分母的值就越大,单位总产值能耗就越低,但这并不意味着综合单耗就越低。本文通过一个简化的例子予以说明。
例如两个企业1和2,都生产产品A和产品B,有关生产数量、产品单耗、产品价格的情况见表1。
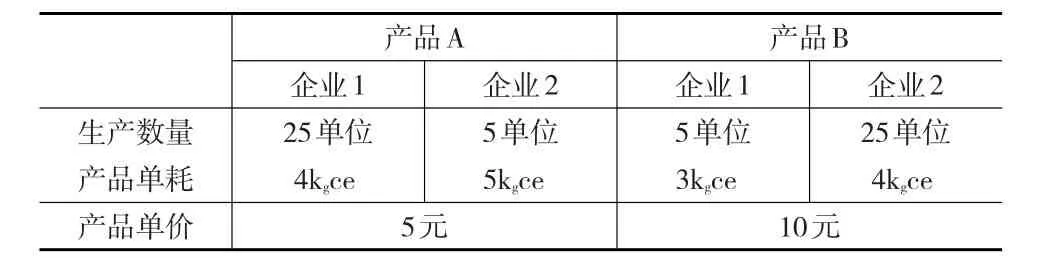
表1 两个企业的生产状况数据
企业1两种产品的单耗都要低于企业2,显然,企业1比企业2具有更低的单耗水平或更优的能效。
如果以总产值综合能效指数(IG)衡量,计算得到两个企业的综合能效指标及指数为:

据此,得到的结论是:企业2的表现优于企业1,综合能效更优。显然,这与实际相违。从公式(1)可以看出,产品单耗U、价格P和产量Q都会对该指数产生影响。在产品单耗一定的前提下,价格高的产品生产的越多,综合能效就越优。
以上是企业之间的横向对比。从纵向比较来看,假如企业1在报告期两种产品的价格和单耗都不变,生产结构的调整也会使其综合能效指数发生变化。基期,企业1依然生产A产品25单位,每单位要消耗能源4kgce,生产B产品5单位,每单位消耗能源3kgce;报告期,企业1少生产价低的A产品5单位,多生产价高的B产品5单位,则报告期和基期该企业的综合能效指标及指数分别为:
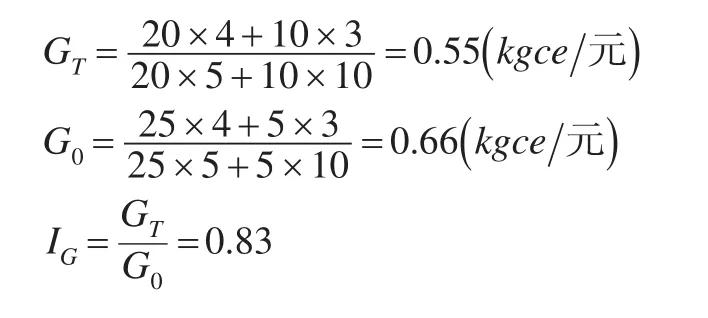
报告期企业1的综合能效改进了,但是,该企业两种产品的单位能耗都没有下降,总产值综合能效指数失真。为了体现综合能效的改善,企业1并不需要真正降低各种产品的单位能耗,只需要调整产品结构,生产更高比重的价高产品即可。
再从价格变动角度看,如果价格指数缩减不能真正反映价格变动水平,总产值综合能效指数也不能反映综合能效的真实变动。例如,上述企业1,假定报告期其产品单耗和生产结构都不变,只有产品价格发生变化,产品1的价格上涨10%,达到5.5元,产品2的价格上涨20%,达到12元,如果能够正确对价格变动进行缩减,则报告期综合能效指标值应保持不变,或者综合能效指数应该为1。
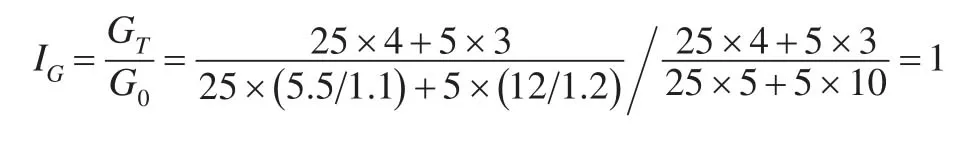
如果缩减时利用的价格指数被低估了,两种产品的价格指数低估为5%和15%,则综合能效指数为:
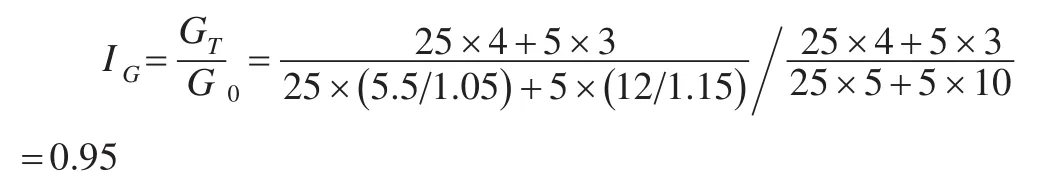
据此得出错误结论,报告期比基期综合能效优化了。综上,综合能效的好转除了产品单耗下降之外,还可由以下两种情况导致:一是调整产品结构,生产更多的高价产品;二是低估价格缩减指数,而这两种方法促成的综合能效的提升显然并非实际综合单耗的下降,因此,用总产值和增加值能效指标构建的综合能效指数受到产品单耗、价格指数、以产值计算的生产结构三方因素的综合影响,无法直接、真实地反映综合能效的变化。
3 能值型综合能效指数的编制构想
3.1 能值型综合能效指数的构造
总产值型综合能效指数存在上述问题的原因在于以Pi作为同度量因素存在的内在缺陷。将式(1)变形为:

本文考虑,如果不以价格,而以能值作为同度量因素,就可以避免上述问题。所谓能值,即单位产品的必要能源含量,它是产品和必要能源的交换,就如价格是产品和必要货币的交换。价格是由竞争性的市场决定的,供给和需求的双向出清决定了价格水平,因此,价格并非由某一个企业的生产成本决定,而是由市场一般成本水平来决定。同理,产品的能值,即所谓必要能源含量,也应该由市场一般能耗水平来决定,它是市场均衡的技术条件下生产一单位产品需要消耗的能源数量。实际选取时可以采用中等或一般技术水平企业的产品单耗,或政府职能部门、行业协会、能源机构等相关专业组织制定的指导性单耗,或称标准单耗。能值型综合能效指标(E)和指数(IE)的计算公式如下:
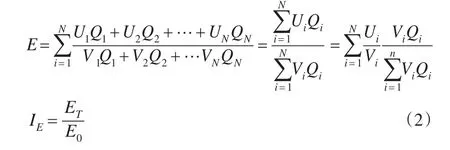
其中:V为产出的能值。使用能值作为同度量因素的好处在于:第一,能值是特定生产过程或特定产品的能耗,不存在重复计算的问题。以上述钢铁行业为例,如果计算钢铁制造业的综合能效,使用的是钢铁生产过程的能值,该值中不涉及铁矿石的能值,因此不会有重复计算,也不会与分子的口径不一致。第二,如前述,在产值型综合能效指标式(1)中,综合能效指数的失真关键在于产品的价格Pi高但是单耗Ui未必高,两者不存在必然的正相关,但是某种产品的能值高,即在社会平均技术水平下,生产一单位该产品的一般单耗越高,则对于某个特定生产者而言,该产品的个体单耗也相应高,Vi和Ui一定是正相关。这样,假如某个产出i的实际单耗Ui高,但匹配的Vi也高,不会出现Ui高Pi可能低的缺陷会降低,权数增加,那么,产出结构更为能源密集型的生产者就不会因较高的个体单耗而获得不利的综合能效值,避免了价值型综合能效指标存在的上述缺陷。实际上,能值型综合能效指标反映了产品篮子的相对综合能效,即以某个主体的个体单耗水平而言,它生产特定产品篮子所需的综合能耗与社会一般技术条件下生产该产品篮子的标准综合能耗的比值。
仍以企业1和企业2为例,假设两个企业有关的生产情况和表1完全一样,生产一单位产品A的能值为4.5kgce,一单位产品B能值为3.5kgce,具体到两个企业,生产产品A的个体单耗都低于产品B。
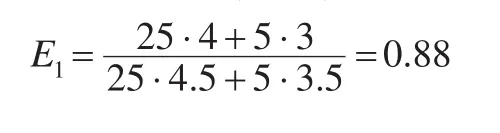

能值型综合能效指数IE的计算结果客观反映了企业1的综合能效水平优于企业2。
3.2 能值型综合能效指数优良性的一般论证
将上述过程推广到一般。仍然是企业1和企业2,都生产产品A和产品B,产品A的单价为PA元,能值为VA,产品B的单价为PB元,能值为VB。企业1生产产品A的数量Q1A单位,每单位要消耗能源U1A,生产产品B的数量Q1B单位,每单位消耗能源U1B;企业2生产产品A的数量为Q2A单位,每单位消耗能源U2A,生产产品B的数量为Q2B单位,每单位消耗能源U2B。假设企业1的单耗优于企业2,简化起见,假设至少有一种产品的单位能耗不高于企业2,这就包括以下几种情况:
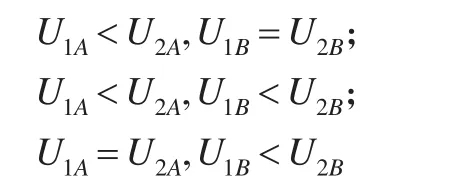
并且,一般情况下,生产产品A的单耗高于产品B,即VA>VB,因此,对于两个企业,都有:UA>UB,但是PA与PB的大小关系不确定。
分别计算两个企业的能值型综合能效指标(E1和E2)和产值型综合能效指标(G1和G2):

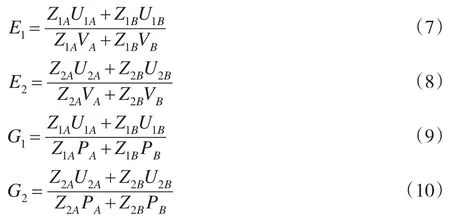
Z为比例系数,没有统计意义只有数量意义。企业1生产的能值高产品的比重大,企业2的小,即:
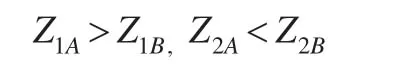
由于能值高的产品特定能耗也高,对于两个企业都有:
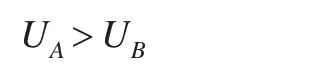
分别计算能值型综合能效指数和产值型综合能效指数得到:


式(11)和式(12)的值哪个大于1,哪个指数就能够正确反映企业1的综合单耗高于企业2的事实。对于式(12),W是两个企业实际总能耗的比值,该值大于1;如果PA<PB,由于Z1A>Z2A,可以确定如果PA>PB,则对于式(11),由于能值和实际单耗之间的正相关关系,VA一定大于VB,所以,的值总是大于1。因此,虽然根据公式无法直接确定式(11)和式(12)的值是否大于1,但是可以比较式(11)和式(12)哪个值会更大,显然,具有更大值的指数更能正确反映企业2的综合单耗高于企业1的事实。两个表达式的左半部分即W相同,式(12)的大于1还是小于1取决于两种产品价格的比较。而对于式(11)中的,由于能值和实际单耗之间的正相关关系,其取值必然大于1。也就是说,针对具体的相关数据进行计算时,如果PA<PB,VA>VB,即产品篮子的价格和能值负相关时,能值型综合能效指数一定优于价值型综合能效指数;而PA>PB,VA>VB时,即价格与能值正相关时,两个指数的变动方向理论上是一致的,无法确定优劣,实际计算结果须视具体数据而定。综上可以得出结论,总体上,能值型综合能效指数优于产值型综合能效指数。
4 能值型综合能效指数的因素分解框架
使用能值型综合能效指数,同样可以对其变动进行因素分解分析。先就能值型综合能效指标而言,理论上说,由于剔除了价格因素的影响,相对于价值型综合能效指标,影响它的因素只有两个,一是产品单耗,二是产品结构。降低产品单耗、生产更多能值低的产品都会引起指标值的下降。将指标变形为:
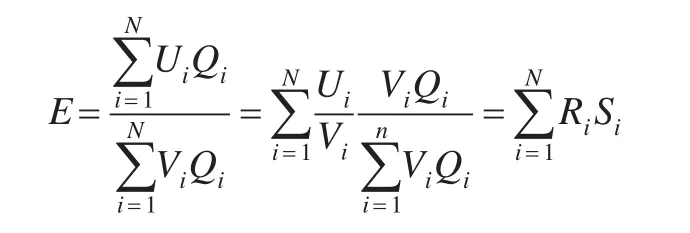
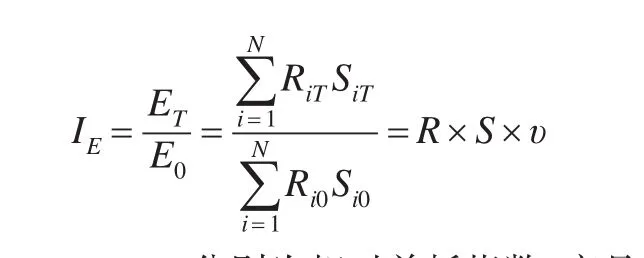
R、S、υ分别为相对单耗指数、产品结构指数和分解残值,相对单耗指数反映各种产品相对单耗的变动对综合能效指数的影响,产品结构指数反映产品结构变化对能值型综合能效指数的影响。
Liu等(2003)[12]曾经总结了能源研究领域使用的八种主要的指数分解方法,其中有四种方法是无残值的,它们是Fisher Ideal、Stuvel、Vartia I和Sato-Vartia方法。该方法针对的是传统的能源强度指数,即增加值综合能效指数,对于部门能源强度和产业结构两因素分解而言,以DI表示总能源强度指数,I表示部门能源强度指数,C表示产业结构指数,则有:
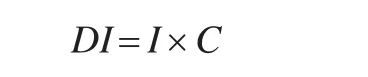
上述分解思路可以直接套用到本文提出的能值型综合能效指数上,此时,被分解的指数是能值型综合能效指数IE,两因素为相对单耗R和产品结构S。利用这四种方法对能值型综合能效指数进行因素分解,得到的有关分解式见表2。
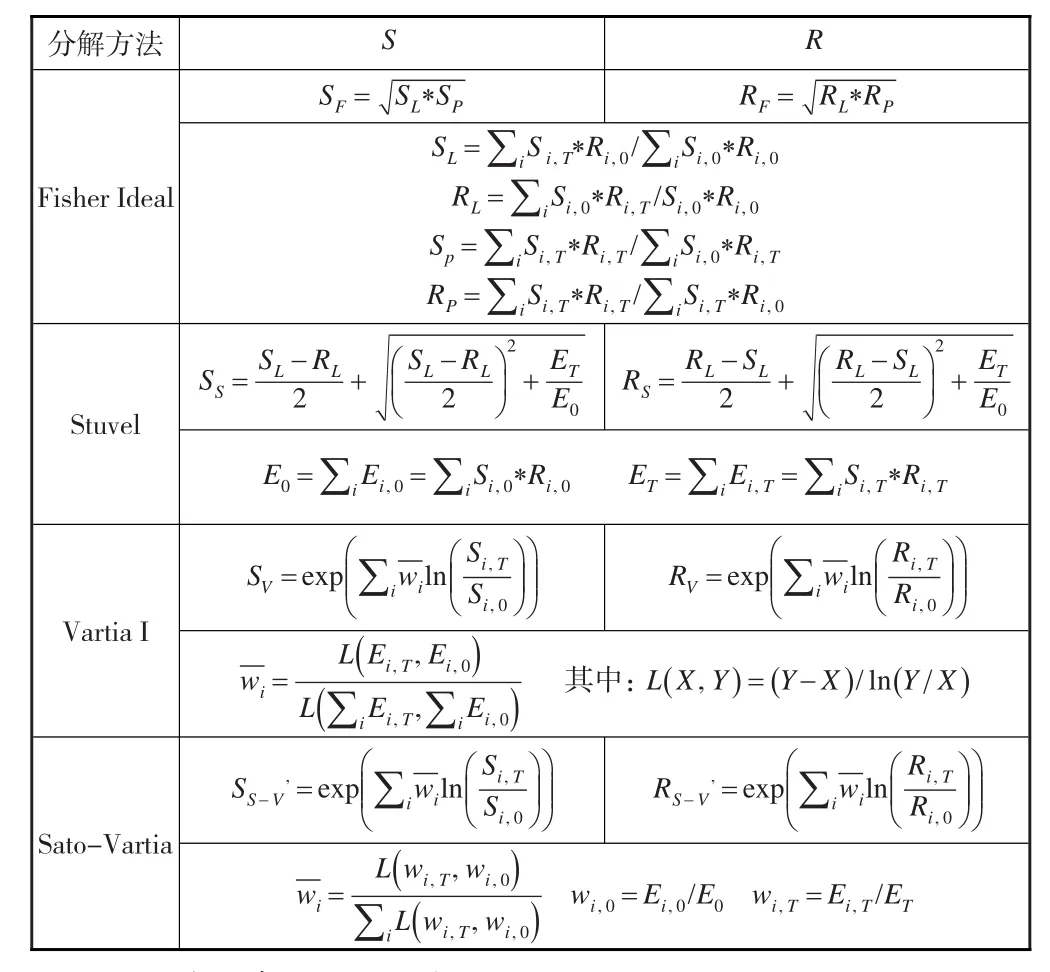
表2 能值型综合能效指数的因素分解式
5 实证分析——以中国钢铁行业为例
根据本文提出的能值型综合能效(以下简称综合能效)指数理论和编制方法,本文以中国六大高耗能行业之一的钢铁工业为例进行了实证分析。受制于数据可得性,选择了2012—2014年这三年作为样本。钢铁工业主要产品产量和相应的实际单耗数据来自于《中国钢铁工业年鉴》。主要产品的标准能耗数据(能值)来自于工业和信息化部颁发的《全国工业能效指南2014》。经过计算得到如下结果。
(1)2012—2014年间,中国钢铁工业的综合能效逐年提升。
2012—2014 年间的综合能效指标值如图1,可以看出,三年的综合能效分别为1.33、1.3和1.26,能源利用效益是逐年提升的。

图1 2012—2014年综合能效指标
(2)产品相对单耗的变动有利于综合能效的优化,但是产品结构的变动不利于综合能效的提升。
利用上述方法,本文进行了2014年与2012年相比的综合能效指数的因素分析,结果见表3。四种分解结果基本上是一致的,体现了分解结果的稳定性。深入来看,能值较高的粗钢产量占比最高、其产量比重的上升对综合能效下降的不利影响较大。此外,能值也较高的高碳烙铁产量比重的大幅上升亦是一个不利因素,它们共同导致产品结构的变化不利于节能降耗。总体上,相对单耗的下降有利于综合能效的提升。除了产量占比很低的电炉锰铁的相对单耗上升较大外,其他产品的相对单耗都是下降的。因此,优化产品结构是钢铁工业今后进一步节能降耗的关键所在。

表3 2012—2014年综合能效指数的因素分解
6 结论
基于统计指数理论编制一个能真实反映综合能源利用效益的统计指数具有十分重要的意义,该指数应该成为经济指数家族的成员。价值型综合能效指数存在的主要问题:一是价值型综合能效指标的分母计算存在问题;二是价值型综合能效指数易受价格和产品结构影响。能值型综合能耗指数采用能值作为同度量因素,能够避免上述缺陷,在真实地反映综合能效变动方面具有更优性。此外,价值型综合能效指数受产品单耗、产品价格、产品结构三因素的影响,而能值型综合能效指数只受产品单耗和产品结构两因素影响,后者更能直接反映综合能效的变化。因此,应重视能值型综合能效指数的编制和应用,使其成为反映综合能效的基本指数。本文以中国钢铁工业为例,应用上述理论和方法进行实证分析的结果表明,2012—2014年,钢铁工业的综合能效是提升的,其中,相对单耗的降低是有利因素,而产品结构的高耗能化是不利因素。
