拓扑绝缘体中的拓扑不变量及其数值计算
2019-03-02何院耀
孙 倩, 何院耀
(1.西北大学 物理学院,陕西 西安 710127;2.中国人民大学 物理学系,北京 100872)
拓扑量子态中没有自发对称性破缺,也没有局域序参量,因而不能用Landau-Ginzburg理论来描述[1-6]。因此,我们需要用某种“全局序参量”来描述拓扑相的物理性质,就是整数化的拓扑不变量。物理上,拓扑不变量与拓扑相中量子化的霍尔电导率直接相关,比如量子霍尔效应中的霍尔电导率和拓扑绝缘体(量子自旋霍尔效应)中的自旋霍尔电导率。
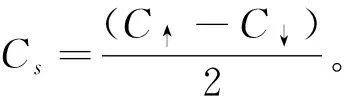
(1)
在下文中,用C表示系统自旋向上或自旋向下部分的陈数,而在具体数值计算中分别计算C↑和C↓,并得到拓扑不变量自旋陈数Cs。由于拓扑不变量只在零温有良好定义,因此,本文的计算都是在零温,对于系统基态的计算。
1 拓扑不变量计算公式
1.1 3种常用公式及其适用条件
针对不同的系统,二维系统中陈数C有多种不同的计算公式,最常见的有以下3种。
第1种计算公式是非常著名的TKNN不变量,在文献[4]中首次从能带理论出发被推导出来。TKNN不变量的原始表达式为
Pst=
(2)
其中,波矢k=(kx,ky),BZ表示倒空间布里渊区,H=H(k)为系统倒空间哈密顿量(矩阵),|t〉,|s〉和Et(k),Es(k)分别为布洛赫本征态和相应的本征能量,即有
H(k)|s〉=Es(k)|s〉H(k)|t〉=Et(k)|t〉。
(3)
TKNN不变量可以进一步写成Berry曲率在系统布里渊区上的积分,如下
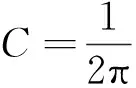
(4)
其中,Ωxy(k)为Berry曲率,a∈Occ表示被占据的能带。
第2种是专门针对两能带系统的计算公式。两能带系统哈密顿量可以简化为H(k)=d(k)·σ+d0(k),其中矢量d(k)=[dx(k),dy(k),dz(k)],σ=(σx,σy,σz)为泡利矩阵组成的矢量,d0(k)为与kx,ky相关的能量常数项(费米能级EF=d0(k))。则该两能带系统的陈数[5]可以表示为
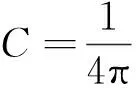
(5)
其中,
d=|d(k)| =
第3种是从零频率单粒子格林函数G(ω=0,k)矩阵出发构造的陈数计算公式[10-18],其表达式为

Tr{P(k)[∂kxP(k)·∂kyP(k)-
∂kyP(k)·∂kxP(k)]}。
(6)
其中,P(k)是由G(ω=0,k)矩阵本征值大于0的本征态构造的投影矩阵
G(0,k)|μi(k)〉=μi|μi(k)〉,
(7)
式(6)中Tr表示对矩阵求迹。
由上面3种不同的拓扑不变量的表达式可以看出,拓扑不变量是对布里渊区的积分,体现出其非局域性。式(4)中的TKNN不变量公式表明,只有费米能级处于系统的能隙中才能得到整数化的陈数,即整数化的拓扑不变量只对于绝缘体才有意义。从计算角度看,第1种计算式(2)需要得到系统的倒空间哈密顿量矩阵,并对角化得到本征值和本征态;第2种计算式(5)需要将倒空间2×2哈密顿量矩阵写成d矢量的形式;第3种计算式(6)需要先计算零频率的单粒子格林函数矩阵,然后构造P(k)投影矩阵;之后的积分计算对于3种公式是相似的。从物理角度看,虽然式(5)只能用于计算两能带系统的拓扑不变量,但是计算相对更简单;式(2)和式(6)均可用于一般的多能带系统。从公式的可扩展性看,式(2)和式(5)均是直接从无相互作用推导而来,只能用于计算无相互作用系统陈数;式(6)从单粒子格林函数出发,可以自然地用于有电子相互作用的系统中。
1.2 3种计算公式等价性的证明
根据上面3种不同的陈数计算公式,接下来证明在无相互作用系统中,式(2)、式(4)和式(5)、式(6)是等价的。
首先,证明在无相互作用两能带系统中,式(2)和式(5)的等价性。两能带系统的倒空间哈密顿量可表示为H(k)=d(k)·σ+d0(k),可得到其两个本征能级和本征态,分别为
E±(k)=d0(k)±d(k),
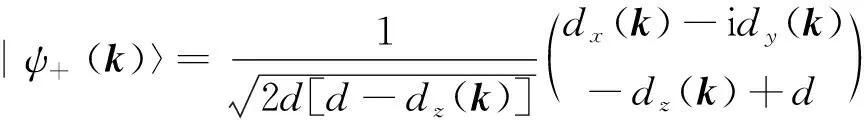
(8)
系统的费米能级EF=d0(k)。式(2)中求和要求Es
(9)
计算倒空间哈密顿量矩阵的一阶导数∂kxH(k)和∂kyH(k)得到
〈ψ-|∂kiH(k)|ψ+〉=
〈ψ+|∂kiH(k)|ψ-〉=
(10)
其中,ki=kx,ky。根据式(10),可以得到
〈ψ-|∂kxH(k)|ψ+〉〈ψ+|∂kyH(k)|ψ-〉-
〈ψ+|∂kxH(k)|ψ-〉〈ψ-|∂kyH(k)|ψ+〉=
[〈ψ-|σα|ψ+〉〈ψ+|σβ|ψ-〉-
〈ψ-|σβ|ψ+〉〈ψ+|σα|ψ-〉]=
〈ψ-|[σα,σβ]|ψ-〉。
(11)
式(11)中的求和共有9项,但是,由于[σγ,σγ]=0,γ=x,y,z,其中只有6项不为零。将式(8)中的两个本征态波函数代入式(11),可得
〈ψ-|∂kxH(k)|ψ+〉〈ψ+|∂kyH(k)|ψ-〉-
〈ψ+|∂kxH(k)|ψ-〉〈ψ-|∂kyH(k)|ψ+〉=
2i{(∂kxdx∂kydy-∂kxdy∂kydx)·〈ψ-|σz|ψ-〉+
(∂kxdz∂kydx-∂kxdx∂kydz)·〈ψ-|σy|ψ-〉+
(∂kxdy∂kydz-∂kxdz∂kydy)·〈ψ-|σx|ψ-〉}=
(∂kxdz∂kydx-∂kxdx∂kydz)·dy+
(∂kxdy∂kydz-∂kxdz∂kydy)·dx}。
(12)
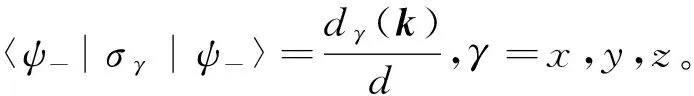
d·[(∂kxd)×(∂kyd)]=
dz(∂kxdx∂kydy-∂kxdy∂kydx)+
dy(∂kxdz∂kydx-∂kxdx∂kydz)+
dx(∂kxdy∂kydz-∂kxdz∂kydy)。
(13)
将式(12)和式(13)代入式(9)得到
(14)
最后,将式(14)的结果代入到式(2)即得到
(15)
式(15)即为第2种陈数计算式(5),由此即证明了式(2)和式(5)在两能带系统中的等价性。
其次,证明在无相互作用系统中公式(4)和公式(6)的等价性。首先,需要计算动量空间单粒子格林函数矩阵G(ω,k),其中ω为一般的复频率。利用格林函数运动方程方法可以得到无相互作用系统G(ω,k)表达式
G(ω,k)=[ω-H(k)]-1。
(16)
其中,H(k)同上为倒空间哈密顿量矩阵。则有零频率单粒子格林函数G(ω=0,k)表达式为
G(ω=0,k)=-[H(k)]-1。
(17)
可见G(ω=0,k)和H(k)矩阵有相同的本征态,且本征值有相应变换关系
H(k)|a(k)〉=Ea(k)|a(k)〉,
G(0,k)|a(k)〉=-[H(k)]-1|a(k)〉=
-[Ea(k)]-1|a(k)〉。
(18)
将式(18)代入式(7)可得
(19)
根据式(19)可以计算P(k)的一阶导数如下
|b(k)〉〈∂kxb(k)|),
|c(k)〉〈∂kyc(k)|)。
(20)
进一步公式(6)中的Trace可以用完备的本征波函数展开来计算,如
Tr[P(k)TxTy]=
Tr[P(k)TyTy]=
(21)
其中,∑k|e(k)〉〈e(k)|=1。在式(21)中,将式(19)结果代入可得
〈e(k)|P(k)=
(22)
将式(22)代入式(21)可得
(23)
式(6)中Trace部分可简化为
Tr{P(k)[∂kxP(k)∂kyP(k)-
∂kyP(k)∂kxP(k)]}=
(24)
根据式(24)结果,需要计算TxTy和TyTx。利用式(20)得到TxTy表达式
TxTy=
|b(k)〉〈∂kxb(k)||∂kyc(k)〉〈c(k)|+
|b(k)〉〈∂kxb(k)||c(k)〉〈∂kyc(k)|}+
(25)
以及TyTx表达式
TyTx=
|c(k)〉〈∂kyc(k)||∂kxb(k)〉〈b(k)|+
|c(k)〉〈∂kyc(k)||b(k)〉〈∂kxb(k)|}+
(26)
可见TxTy和TyTx表达式的求和中均有4项,其中三项是二重求和,一项是一重求和。将式(25)和式(26)结果代入式(24)可得
〈∂kye(k)||∂kxe(k)〉]+
〈e(k)||∂kyb(k)〉〈∂kxb(k)||e(k)〉}。
(27)
式(27)两项相减后,原TxTy和TyTx表达式求和中有两项分别抵消,剩余两项,即为式(27)结果。注意到式(27)结果第二项(即二重求和项)等于0,原因为
〈e(k)||∂kxb(k)〉+〈∂kxe(k)||b(k)〉=
∂kx[〈e(k)||b(k)〉]=0,
〈∂kyb(k)||e(k)〉+〈b(k)||∂kye(k)〉=
∂ky[〈b(k)||e(k)〉]=0。
(28)
由式(28)可得
〈e(k)||∂kxb(k)〉=-〈∂kxe(k)||b(k)〉,〈∂kyb(k)||e(k)〉=-〈b(k)||∂kye(k)〉。
(29)
结合式(29)可以得到
(30)
其中,最后一步相等可理解为将第二步第一项求和中b和d互换,即与第二项求和完全相同,所以结果为0。结合式(24)、式(27)和式(30),可得
Tr{P(k)[∂kxP(k)∂kyP(k)-
∂kyP(k)∂kxP(k)]}=
〈∂kye(k)||∂kxe(k)〉]。
(31)
根据式(4)可计算Berry曲率
〈∂kya(k)||∂kxa(k)〉]。
(32)
结合式(31)和式(32)得到
Tr{P(k)[∂kxP(k)∂kyP(k)-
∂kyP(k)∂kxP(k)]}=iΩxy(k)。
(33)
最后将式(33)结果代入式(6),即得到

Tr{P(k)[∂kxP(k)·∂kyP(k)-∂kyP(k)·∂kxP(k)]}=
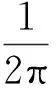
(34)
式(34)结果即为式(4),亦即式(2),由此证明了式(34)与式(2)和式(4)的等价性。
通过以上解析计算,可以发现上述3种不同的计算陈数的公式在无相互作用系统中是完全等价的。其中,式(2)和式(6)也可用于计算多能带系统拓扑不变量;式(6)还可以拓展应用于有相互作用系统中拓扑不变量的计算。
2 应用实例:Kane-Mele模型
2.1 数值计算细节
下面以具体模型为例讨论上述拓扑不变量的数值计算。由于第3种计算式(6)的广泛适用性,在以下的计算中均选用式(6)做数值计算。式(2)、式(4)和式(5)的数值计算与式(6)很相似,这里不做讨论。为不失普遍性,我们选取一般化的Kane-Mele模型(honeycomb晶格)作计算,模型哈密顿量如下
(35)
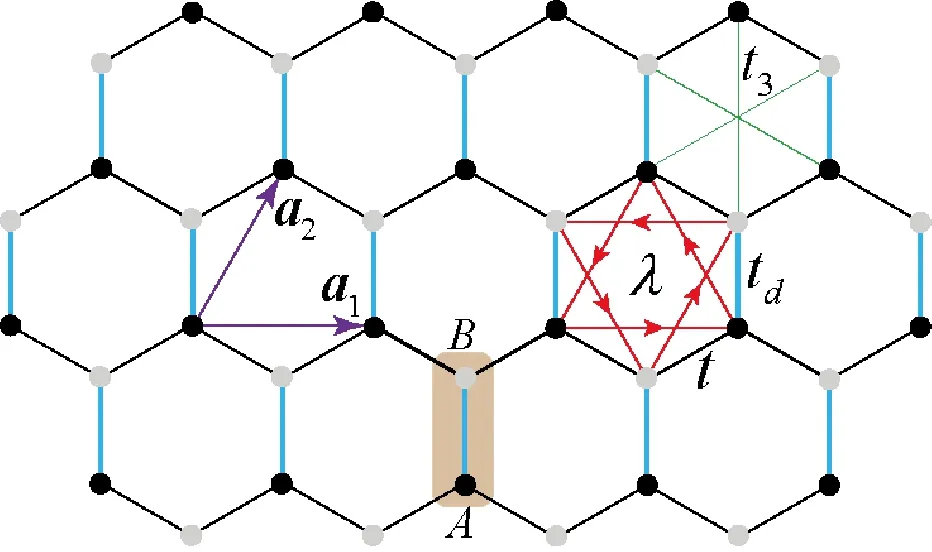
图1 二维honeycomb晶格以及Kane-Mele模型中各项电子跃迁示意图Fig.1 Lattice geometry of 2D honeycomb lattice with hopping parameters in Kane-Mele model
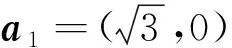
[H(k)]σ=
g(k)=
(36)
其中,自旋向上ξ↑=+1和自旋向下ξ↓=-1。式(6)的数值计算中需要计算布里渊区上的积分,我们用最简单的梯形法作积分,但是,由于honeycomb晶格的布里渊区是平行四边形,而不是矩形,首先,需要做一个Jacobi变换,将系统的布里渊区变成一个矩形,再用梯形法作数值积分。一般地,任何非正方晶格的布里渊区均可由Jacobi变换变成矩形,所以下面的计算可以推广到所有晶格的情形。honeycomb晶格的布里渊区边界为
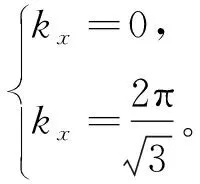
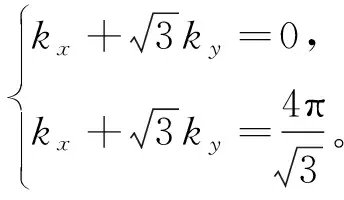
(37)
引入如下的Jacobi变换以及逆变换
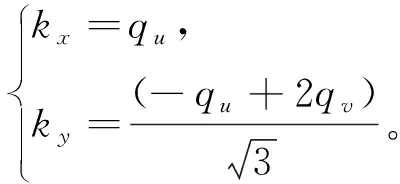
(38)
可得新变量qu,qv取值范围为矩形,即
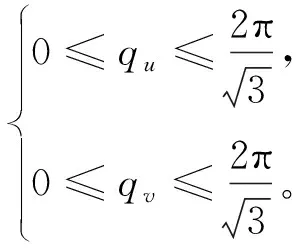
(39)
这个Jacobi变换相应的Jacobi行列式为
(40)
综合式(37)~(40),在honeycomb晶格的布里渊区上的积分可以转化为矩形区域的积分
I=∬k∈BZf(kx,ky)dkxdky=
(41)
其中,有
(42)
将式(41)和式(42)代入式(6)可得
C=∬k∈BZf(kx,ky)dkxdky=
(43)
其中,
Tr{P(k)[∂kxP(k)·∂kyP(k)-∂kyP(k)·∂kxP(k)]}。
(44)
为方便数值计算,需要将P(k)对kx和ky的一阶导数转化为对qu和qv的一阶导数。引入Q(qu,qv)函数矩阵,
Q(qu,qv)。
(45)
计算P(k)对kx和ky的一阶导数为
(46)
将式(46)代入式(44),得到
Tr{P(k)[∂kxP(k)·
∂kyP(k)-∂kyP(k)·∂kxP(k)]}=
(47)
将式(47)代入式(43),即可得到陈数表达式为
∂quQ]}。
(48)
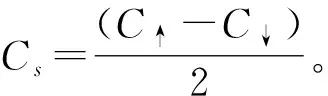
2.2 计算结果
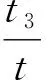
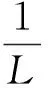
2)在每个对应的绝缘体相中,自旋陈数在热力学极限下都是整数化(量子化)的;
3)在不同绝缘体之间的拓扑相变处,自旋陈数具有跳变,这个跳变是拓扑相变基本的特点之一。
由此可见,上述自旋陈数Cs有效和正确地描述了Kane-Mele模型的完整相图。
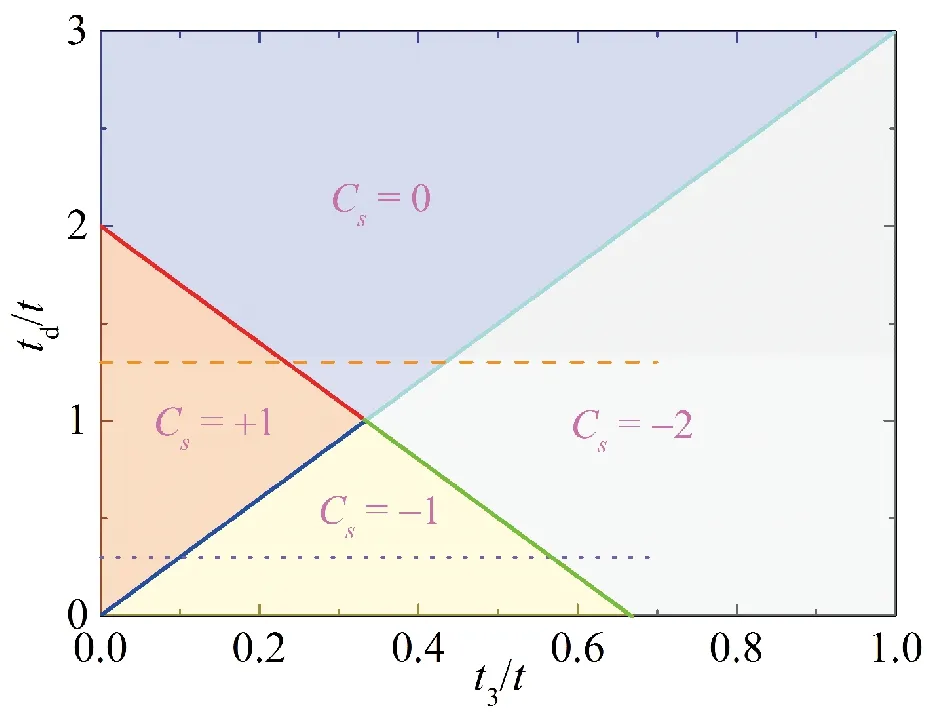
图2 Kane-Mele模型t3-td相图(λ=0.2t)Fig.2 The t3-td phase-diagram of Kane-Mele model with λ=0.2t
通过以上Kane-Mele模型中拓扑不变量的计算,检验了上述拓扑不变量的计算范式,展示了计算方法的正确性。
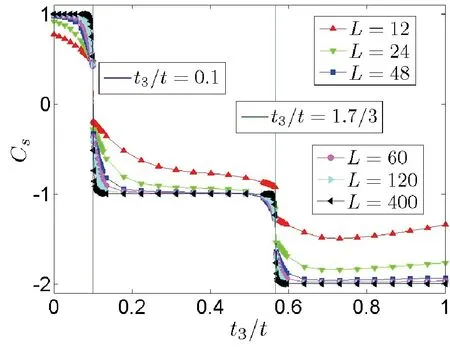
图自旋陈数Cs的计算结果Fig.3 Results of calculated spin Chern number Cs for with λ=0.2t
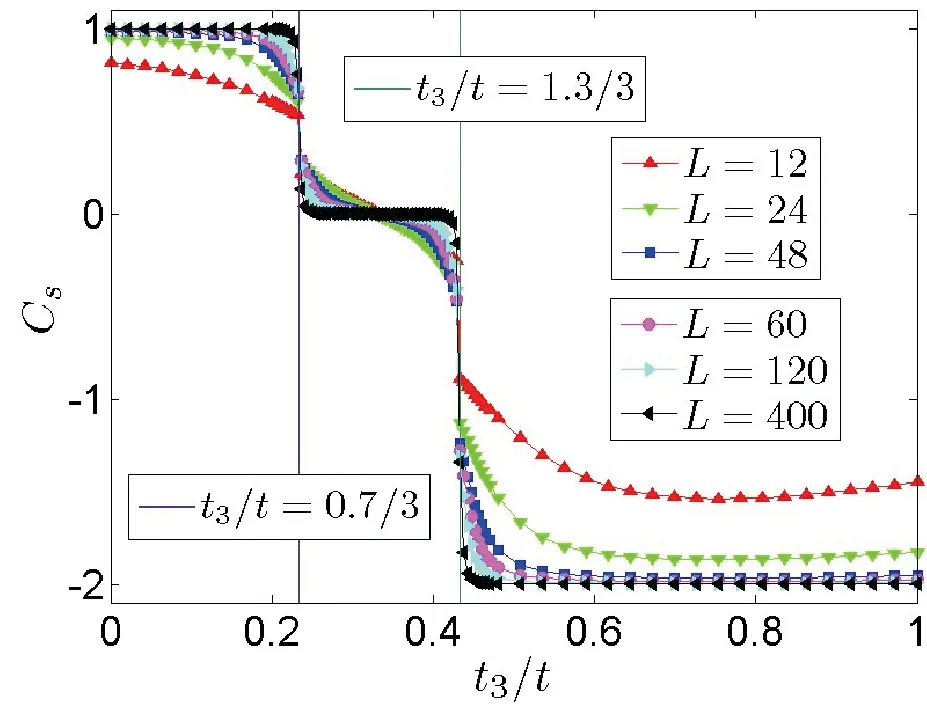
图自旋陈数Cs的计算结果Fig.4 Results of calculated spin Chern number Cs for with λ=0.2t
3 结 语
首先,证明了在无相互作用系统中,常用到的3种拓扑不变量计算公式的等价性,并给出了详细的证明推导过程;其次,我们给出了从零频率单粒子格林函数出发推导的拓扑不变量公式的完整数值计算过程;最后,用拓扑不变量公式做了Kane-Mele模型中拓扑不变量的数值计算,根据拓扑不变量的值计算出了Kane-Mele模型的完整相图,展示了本文中阐述的计算拓扑不变量方法的有效性和正确性。本文的工作对于无相互作用拓扑绝缘体系统的研究,特别是分类有比较重要的意义。此外,何院耀在文献[19-20]中详细研究了利用式(6)结合量子多体数值计算方法(如量子蒙特卡洛算法)计算有相互作用拓扑绝缘体系统的拓扑不变量,与本文的工作形成互补。这些工作连同本文工作一起,共同构成了计算拓扑绝缘体(无相互作用和有相互作用)系统中拓扑不变量的一套完整的方法,对于拓扑绝缘体的研究具有重要意义。
