基于PSM和DID法的湿地自然保护区保护效果分析——以黑龙江省三江和挠力河国家级自然保护区为例

刘子刚,王 琦,彭爱珺,杨 飞

(1.中国人民大学 环境学院,北京 100872;2.中国科学院 地理科学与资源研究所,资源与环境信息系统国家重点实验室,北京 100101)

建立湿地自然保护区是湿地保护的最主要的手段之一[1]。截至2015年底,我国已建立湿地自然保护区600多个,湿地保护面积2 391万hm2,湿地保护率为44.60%[2]。科学地评估自然保护区的保护效果对于湿地有效保护和管理具有重要意义。

国内外研究主要从生物多样性[3-8]、景观格局变化[9-19]、生态系统价值和健康[20-23]等方面,通过对保护区建立前后变化或者保护区内外差异的对比评估自然保护区的保护效果。但是,由于保护区建立前后,区内外自然禀赋存在差异会导致评估结果产生选择性偏差[24-25]。

双重差分(difference in difference, DID)模型[26]和倾向得分匹配(propensity score matching,PSM)模型目前在已广泛应用于政策和项目评估,涵盖经济学[27-31]和社会学领域[32-36],资源环境[37-42]领域也有涉及。双重差分模型原理借鉴自然实验方法,选取不受政策影响的对照组,将两组的同一指标的变化量进行比较,差值就是该项目或政策的真实效果[43]。倾向得分匹配法的原理是找到与实验组(treatment group)所有相关的预处理特征类似的对照组(control group),对照组产生的不同结果就可以归因于该项目[44]。该方法的主要特点在于通过匹配变量的选取控制可观测变量对估计结果的影响[45]。

本文运用遥感数据对黑龙江省三江和挠力河国家级湿地自然保护区建立前后湿地变化特征进行描述性统计,运用线性回归模型、多项Logit模型、双重差分模型、倾向得分双重差分模型评估自然保护区的保护效果,并对结果进行对比分析,试图找到科学的方法得出更加真实的结果,为湿地自然保护区的建立和有效管理提供科学依据。

1 研究区概况

本文选择三江国家级自然保护区和挠力河国家级自然保护区为研究区。这两个保护区位于黑龙江省东北部三江平原腹地,是三江平原典型湿地的代表。研究区地理位置见图1。

图1 研究区地理位置Fig.1 Location of the study area

1.1 基本情况

三江自然保护区面积为198 100.00hm2,地理位置为46°40′N～46°52′N,132°05′E～132°26′E,平均气温2.2℃,平均海拔50.00m,年降水量540.00 mm;挠力河自然保护区面积160 595.40 hm2,地理位置为46°30′N～47°22′N,132°22′E～134°10′E,平均气温2.31℃,平均海拔50.00m,年降水量546.00 mm。两个自然保护区地理位置接近,均为内陆湿地与水域生态系统,气候均为温带大陆性季风气候。但两个保护区建立时间不同,三江自然保护区建立于1994年,挠力河自然保护区建立2002年(国家级)。因此,本文将挠力河自然保护区作为对照区,分析三江自然保护区的保护效果。

1.2 湿地变化情况

图2 三江和挠力河自然保护区1980—2000年湿地率变化Fig.2 The changes of wetland rate in Sanjiang and Naolihe Nature Reserve from 1980 to 2000

图2显示了1980—2000年三江和挠力河保护区湿地率变化情况。可以看出,整个三江平原湿地率较低,且一直呈现下降趋势。1980—1990年,三江与挠力河自然保护区均未成立,湿地率均大幅下降。其中,三江自然保护区下降幅度较大,由96.53%下降到86.10%;挠力河自然保护区由87.28%下降到84.69%。1990—2000年,三江自然保护区(建立于1994年)湿地率略有上升,由86.10%上升到86.49%,增加了0.39%;挠力河自然保护区此时尚未建立,湿地率下降幅度较大,由84.69%下降到80.68%。这说明,从1980—1990年湿地变化情况来看,三江自然保护区的建立是有效果的。但是,由于存在选择性偏差,为了得到更为真实的保护效果,需要进行进一步的分析。

2 变量选取与数据来源

选择湿地面积作为因变量,海拔、坡度、距河流的距离、径流量、距居民点的距离、人口数量和GDP等作为自变量。考虑到保护区周边为国有农场,农业机械化比较发达,本文选取农业机械总动力反映农业生产对保护区的影响,变量具体情况如表2。

自然地理数据来源于中国科学院地理科学与资源研究所，以GIS和RS技术为支撑,基于三江平原1990年、2000年土地利用现状图及LandsatTM/ETM+遥感影像图,提取了两个自然保护区的湿地面积和湿地率数据。社会经济数据来源为黑龙江统计年鉴和黑龙江垦区统计年鉴。

利用ArcGIS软件的渔网分析功能将两个保护区划分为100m×100m的像元,将两个保护区的像元分别编号,三江自然保护区划分为192 947个像元,挠力河自然保护区204 771个像元,提取每个像元的属性信息,包括海拔、坡度、距最近河流距离、距最近居民点距离、径流量、湿地面积等。其中,径流量由降水量和蒸散量的差值得到。GDP、人口数据等结合土地利用数据和夜间灯光数据通过ArcGIS软件中计算得到。

3 模型构建

为了科学地评估保护效果,选取多项Logit模型、线性回归模型、双重差分模型和倾向得分匹配模型分别对保护区的保护效果进行分析。

3.1 线性回归模型

将自然保护区建立与否作为自变量,湿地面积作为因变量进行线性回归,并控制尽可能多的变量以减少遗漏的变量误差,建立模型如式(1)。

WAi=α0+α1Policyi+α2Dst_Riveri+α3Net_flowi+α4Demi+α5Slope5i+α6Dst_peoplei+α7Ag_mαi+α8GDPi+α9Popi+εi

(1)

式中:Policyi是虚拟变量,像元i位于三江自然保护区为1,位于挠力河自然保护区为0;Dst_Riveri是像元i距河流的距离;Dst_peoplei是像元i距居民点距离;Net_flowi是像元i的径流量;Demi是像元i的海拔;Slopei是像元i的坡度;Popi是像元i的人口数量;GDPi是像元i的GDP;Ag_mαi是像元i的农业机械总动力;α1～α9是系数。

3.2 多项Logit模型

多项Logit模型可以通过对比不同时间段各种因素对湿地变化的影响。选择三江自然保护区建立前的时间段1980—1990年,以及建立后的时间段2000—2010年,将湿地面积变化划分为多值变量,湿地面积不变,定义为0,概率为P0;面积增加为1,概率为P1;面积减少为2,概率为P2。自变量均取不同研究时间段的均值。模型如式(2)和式(3)。

(2)

(3)

式中:Popi是像元i的人口数量,GDPi是像元i的GDP,Ag_mαi是像元i的农业机械总动力。β1，β2，β3是系数,反映了各自变量对因变量的影响方向和大小。

3.3 双重差分模型

双重差分模型借鉴了自然实验的方法,建立实验组与对照组,将建立保护区的真实影响分离出来。为反映三江自然保护区建立前后的变化,选取其建立前的1990年与建立后的2000年的数据,构建双重差分模型如式(4)。为了更好地估计保护区建立的政策效果,控制了影响湿地面积变化的其他因素。

WAit=α0+α1policyi+α2yeart+

α3policyi·yeart+α4Xit+εit

(4)

式中:WAit是像元i的湿地面积;policyi是保护区虚拟变量,当像元i位于三江自然保护区内,取值为1,反之为0;yeart是时间二值虚拟变量,保护区建立后,t=2,yeart=1;保护区建立前,t=1,yeart=0;policyi·yeart是时间与保护区虚拟变量的乘积;Xit是一组随时间变化的可观测的影响变量Yit的控制变量。

选取挠力河自然保护区作为对照组,两个保护区对比的保护效果为:

ΔWA1-ΔWA2=α3+Δε1-Δε2

(5)

式中：ΔWAi=WAi2-WAi1。由式(5)可见,建立保护区变量和时间的交互项系数α3即为真正用来度量实验组政策效应的量。

3.4 双重差分倾向得分匹配模型

双重差分倾向得分匹配模型是对双重差分模型进一步修正,消除选择性偏差,使保护区建立成为随机事件,能够得出更为真实的建立保护区的政策效果。具体步骤为:

1)以保护区为因变量,建立Logit回归模型。模型的一般公式为

(6)

其中,Y为因变量,即是否建立自然保护区的二维虚拟变量,保护区内为1,反之为0;Xi为一组协变量,即研究对象的一些基本特征变量,为径流量、坡度、湿地距居民点的距离、湿地率。利用公式(6)进行Logit回归得出各协变量回归估计的系数。

2)计算各个研究对象的倾向得分。将第一步中回归估计出系数带入到原方程中,并将各个研究对象协变量的取值带入。

3)依据计算所得的倾向得分,进行匹配,得到实验组和对照组。

4)匹配后剔除多余数据直接进行双重差分模型计算。

4 结果分析

4.1 倾向得分估计结果

以建立保护区为因变量,三江保护区为实验组,赋值为1;挠力河为对照组,赋值为0。选取坡度、距居民点距离、径流量、湿地率等变量进行倾向得分匹配。使用保护区建立前的1990年数据,利用stata14.0软件进行统计。Logit回归结果(表1)显示,选取的协变量回归系数均显著,说明协变量均对保护区的建立有显著的影响,保护区建立与上述因素存在相关性,建立保护区不是随机事件。

为考察匹配效果,采用核密度函数图(图3)进行匹配平衡检验。由图3可见,匹配前,实验组和对照组的倾向得分值的概率分布存在明显若异,说明出现样本选择偏误问题,如果选取两组样本进行分析,得到的计量估计结果存在偏误,这也说明如果直接采用双重差分模型进行保护效果评估其结果存在混杂偏误。然而,进行匹配之后,实验组和对照组的差异大幅度降低,两组样本倾向得分值的概率分布更加接近,说明得出较为合适的匹配样本,匹配效果较好。

表1 Logit回归估计结果Tab.1 Results of Logit regression model

4.2 不同模型结果比较

多项Logit模型、线性回归模型、DID模型和PSM+DID模型结果比较如表2。

多项Logit模型通过比较两个时间段保护区像元GDP、人口、农业机械总动力变化引起面积变化的可能性,来比较保护区保护效果。对于面积增加的像元,随着GDP的增加,湿地面积增加的可能性变小。建区前,湿地面积增加的概率减少12.4%,建区后则减少87%。对于面积减少的像元,建区前,GDP增加会使面积减少的概率减少97.9%,建区后则增加2.4%。人口与农业机械总动力的变化对湿地面积变化的影响均会随着保护区的建立而变小,说明保护区建立会使得人为因素对湿地面积的改变的影响变小。

线性回归模型结果表明,建立保护区对2000年的湿地面积产生了负向影响,即建立保护区会比不建保护区湿地率减少1.85%,且在1%的水平下显著,说明保护区建立并没有起到保护效果。

双重差分模型结果可知建立保护区导致湿地面积增加,且在1%的水平下显著,建立保护区比不建保护区湿地率增加4.67%。

PSM+DID模型结果表明建立保护区导致湿地面积增加,且在1%的水平下显著,建立保护区比不建保护区湿地率增加6.18%。

图3 核密度函数图Fig.3 Kernel density function

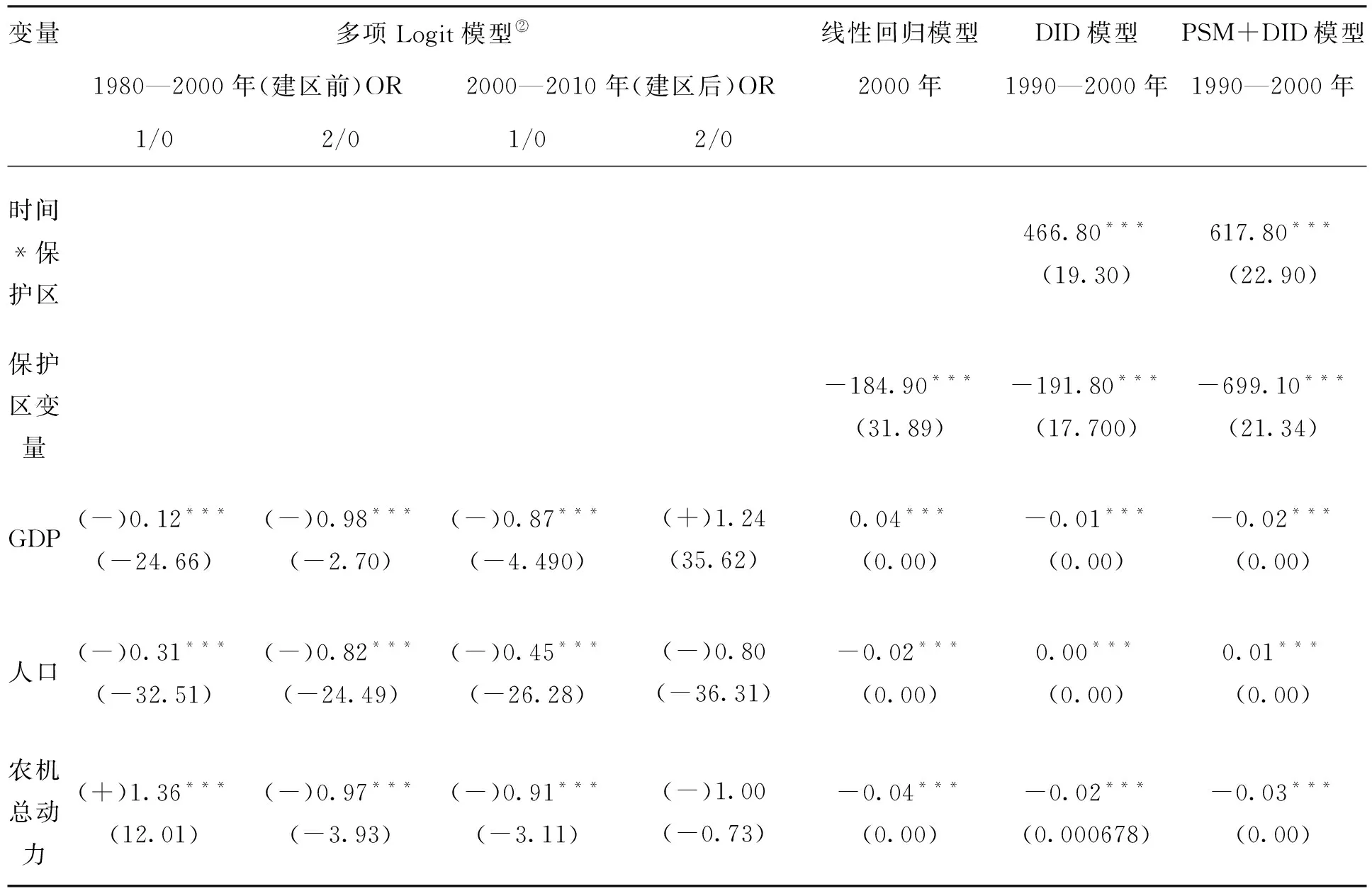
变量多项Logit模型② 线性回归模型DID模型PSM+DID模型 1980—2000年(建区前)OR 2000—2010年(建区后)OR 2000年 1990—2000年 1990—2000年 1/02/01/02/0时间*保护区 466.80***(19.30)617.80***(22.90) 保护区变量 -184.90***(31.89)-191.80***(17.700)-699.10***(21.34) GDP (-)0.12***(-24.66)(-)0.98***(-2.70)(-)0.87***(-4.490)(+)1.24(35.62)0.04***(0.00)-0.01***(0.00)-0.02***(0.00) 人口 (-)0.31***(-32.51)(-)0.82***(-24.49)(-)0.45***(-26.28)(-)0.80(-36.31)-0.02***(0.00)0.00***(0.00)0.01***(0.00) 农机总动力 (+)1.36***(12.01)(-)0.97***(-3.93)(-)0.91***(-3.11)(-)1.00(-0.73)-0.04***(0.00)-0.02***(0.000678)-0.03***(0.00)

续表2

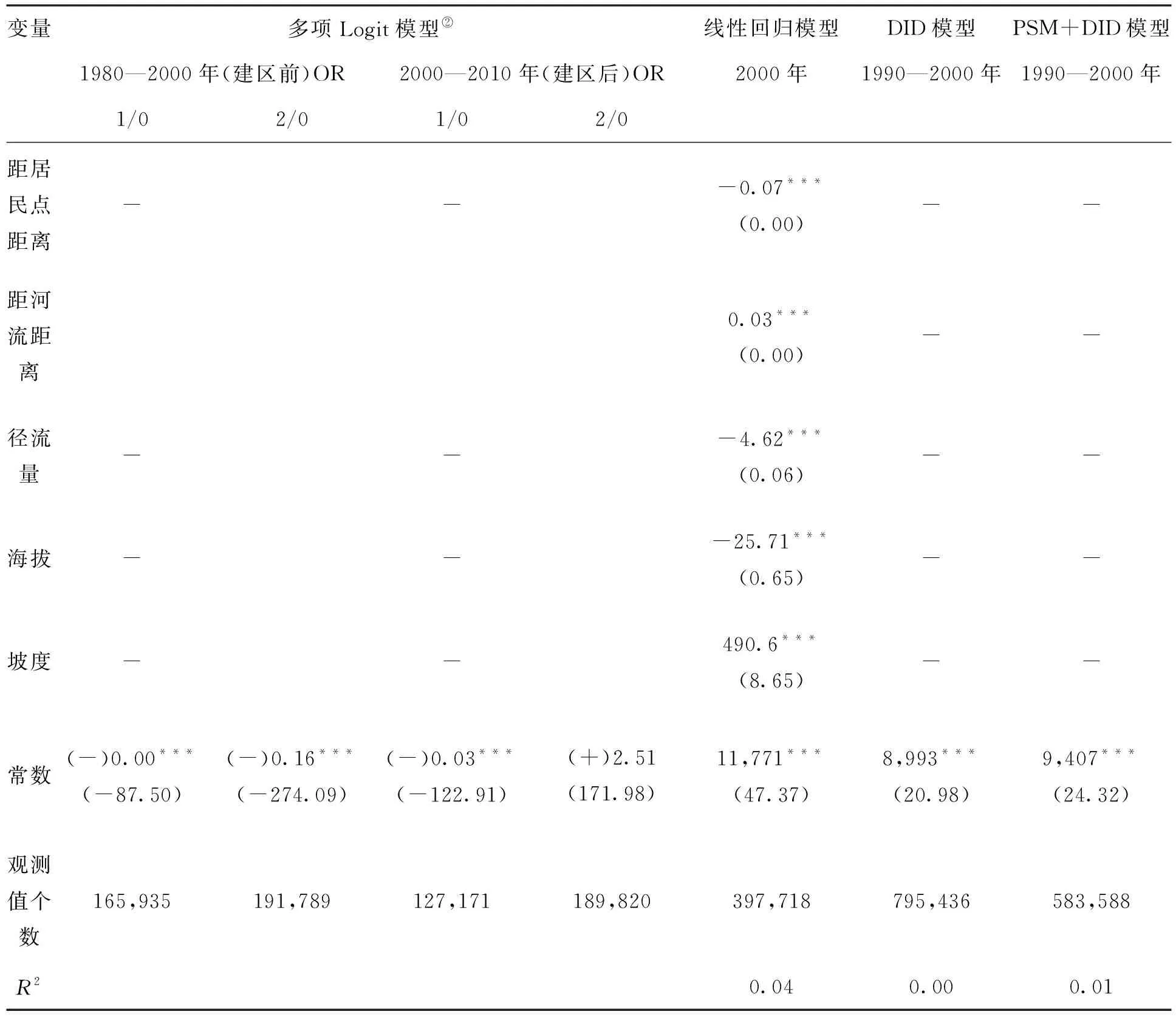
变量多项Logit模型② 线性回归模型DID模型PSM+DID模型 1980—2000年(建区前)OR 2000—2010年(建区后)OR 2000年 1990—2000年 1990—2000年 1/02/01/02/0距居民点距离 ---0.07***(0.00)--距河流距离 0.03***(0.00)-- 径流量---4.62***(0.06)-- 海拔---25.71***(0.65)-- 坡度--490.6***(8.65)-- 常数(-)0.00***(-87.50)(-)0.16***(-274.09)(-)0.03***(-122.91)(+)2.51(171.98)11,771***(47.37)8,993***(20.98)9,407***(24.32) 观测值个数165,935191,789127,171189,820397,718795,436583,588 R20.040.000.01

注:① 系数下面括号内数字表示标准差,*表示10%水平下显著,**表示5%水平下显著,***表示1%水平下显著。② 在多项Logit模型中,括号内为系数的正负,反映自变量对因变量影响的方向;OR(Odds Ratio)为几率比,反映影响的大小。1/0表示面积增加和面积不变的比率P1/P,2/0表示面积减少和面积不变的比率P2/P。

5 结论与讨论

从湿地变化情况来看,1980—1990年,三江与挠力河自然保护区湿地率均大幅下降;1990—2000年,三江自然保护区湿地率略有上升,增加了0.39%;而挠力河保护区湿地率仍在下降。说明三江自然保护区的建立以后,湿地退化的趋势有所减缓。但是,从湿地变化情况并不能得出保护区建立的真实效果。

为了得到更为真实的保护效果,本文采用线性回归模型、多项Logit模型、双重差分模型、倾向得分匹配双重差分模型对三江自然保护区的保护效果进行了分析。不同模型的结果具有显著差异。多项Logit模型从时间跨度对比得出建立保护区会使人为干扰因素对湿地面积变化产生的影响缩小,保护效果为正,但该模型无法满足保护区建立前后其自身禀赋相同的条件;线性回归模型的结果表明建立保护区会比不建保护区湿地率减少1.85%,但该模型的分析并未涉及时间前后对比,未考虑政策的滞后性;双重差分模型结果表明建立保护区比不建保护区湿地率增加4.67%;双重差分倾向得分匹配模型结果表明建立保护区比不建保护区湿地率增加6.18%。

建立自然保护区是一个非随机过程,寻找对照组对于分析建立保护区的政策效果十分重要,一般来讲无法做到使实验组和对照组完全一致。运用双重差分模型和倾向得分匹配模型,目的是创造一种自然实验,在实验区和对照区选择具有可比性的样本进行分析,使保护区建立成为一种随机过程。通过本研究发现双重差分模型和倾向得分匹配模型应用于湿地保护效果评估是适用的,能够有效降低选择性偏差,从而得到更加真实的保护效果。