基于小波相干分析的阵发性房颤自动检测方法
2019-03-02孙亚楠韦杰英
王 迪,李 强,孙亚楠,韦杰英,张 瑞
(西北大学 医学大数据研究中心, 陕西 西安 710127)
心房颤动(atrial fibrillation, AF),简称房颤,是临床上最为常见的心律失常之一,往往会导致严重的并发症(如心力衰竭和中风等)[1]。心电图(electrocardiogram,ECG)是由心电图仪记录反映心脏兴奋的电活动过程,对房颤的诊断与治疗具有重要的参考价值[2]。图1显示一个正常心动周期内的心电图波形,其中P波表示心房去极化过程,QRS复合波表示心室去极化过程,T波表示心室复极化过程。房颤发作时,心电图的改变主要表现在两个方面:①RR间期绝对不规则;②P波缺失,代之以大小不等、间距不均、形态各异的f波。图2显示了正常心律和心房颤动的心电图片段。
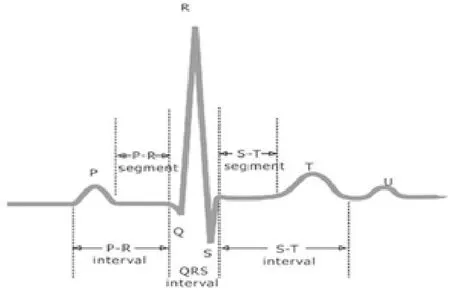
图1 一个正常心动周期的心电图波形Fig.1 ECG of a normal cycle
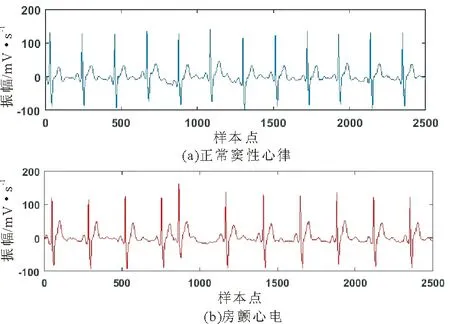
图2 窦性心律与房颤心电Fig.2 Sinus rhythm and atrial fibrillation
根据房颤发作持续时长,可分为阵发性房颤、持续性房颤和永久性房颤。其中阵发性房颤发作突然且持续时间短暂,临床上易被漏诊,因此往往需要长时程的心电监测。传统的房颤检测主要是医生根据经验进行视觉诊断,但长时程的心电数据使得这一过程较为耗时。此外,仅依靠视觉观察往往难以捕捉阵发性房颤在心电图上所表现出的短暂且微弱的波形变化,从而造成较多漏诊。因此,研究阵发性房颤的自动检测具有十分重要的临床意义。
关于阵发性房颤自动检测的研究可大体分为两类:基于RR间期不规则的方法和基于P波缺失的方法。1983年Moody G.B.采用马尔可夫过程模型对RR间期序列进行分解并得到RR间期预测数组,当该数组的平均误差超过某一给定的阈值时,则认为对应于一个房颤片段[3]。Duverney D. 利用小波多尺度分析技术将RR间期时间序列分解成不同的频域水平,进而突出高频段的房颤起点与终点,最后利用分形法来分类窦性心律与房颤[4]。Tateno K.等提取了RR间期和RR间期差的房颤标准密度直方图,并采用柯尔莫哥洛夫史密诺夫检验评估待测密度直方图与标准直方图的差异度,如果差异度小于某一给定的阈值,则认为该段信号为房颤心电[5]。然而,值得注意的是,RR间期不规则并非唯一对应于房颤,这一现象也会出现在其他心律失常之中(如房扑、多源性房速等)。此外,当房颤发作时,如果出现房室传导阻滞等心脏异常情况时,其心电图中RR间期也可能是规则的。因而,仅依赖房颤不规则这一特征显然不能全面刻画房颤。基于此,结合心房活动(即P波特征)进行研究分析可大大提高房颤检测的准确率[6]。已有的基于P波特征的房颤检测方法主要分为两类:时域法和频域法。时域法主要是对P波间期、P波离散度、P波变异性等概念进行定量分析。此类方法对P波形态的依赖性较小,而且重复性较好。其中P波离散度最早由Dilavefis P.E.等人提出,是指在常规的12导联心电图中最大与最小P波间期之差,其基准值一般设定为4s[7]。P波变异性[8]由Andrikopoulos G.K.等人中提出,将其定义为P波间期标准差的平方。该参数类似于P波离散度,能够反映心房活动在传导过程中的变异性。频域法则是通过对心电图中的P波或f波作快速傅里叶变换,比较分析房颤发作时各个频域段的特征进行房颤检测。文献[9]和[10]利用傅里叶变换对信号时域和频域之间进行全域变换,进而对信号进行相干分析后得到时间段内的相干系数。Ortigosa等人对心电信号进行广义傅里叶变换,提取心房活动特征并结合支撑向量机完成阵发性房颤的自动检测[11]。白鹏飞等人利用小波包变换处理滤波后的心电信号,同时重构出P波主频带波形并确定P波的始末位置,最后将所提取P波的形态学特征与人工神经网络结合完成阵发性房颤的自动检测[12]。
为了充分运用心电信号的时频局部特性及瞬时特性,本文提出一种基于小波相干分析的阵发性房颤自动检测方法。首先,对所有的心电信号进行预处理,包括去除噪声、分段处理、选取模板等;其次,对模板与待测心电信号进行小波相干分析得到小波相干图;进而,计算小波相干值的均值、比率以及交叉小波相位角方差,构成房颤心电特征;最后,将所提取特征结合超限学习机完成阵发性房颤的自动检测。
1 方 法
阵发性房颤自动检测的本质就是一个两类分类问题。本小节将系统介绍相关基础理论知识、心电信号的预处理、房颤心电特征提取方法以及超限学习机。
1.1 理论基础
1.1.1 连续小波变换 连续小波变换(continuous wavelet transform, CWT)是一种时间窗和频率窗都可改变的局部化分析方法[13],可以在预先定义的尺度上对原始信号进行多尺度滤波,能够对非平稳的心电信号由粗及细地进行局部化分析[14-15]。
给定一段心电信号x(t)∈L2(R),则该心电信号的连续小波变换可以定义为
(1)
式(1)中:a为尺度因子,b为平移因子,Ψa,b(t)为小波基函数。通过对信号进行连续小波变换,可以得到信号在不同尺度下对应带通的信息。
1.1.2 小波相干分析 小波相干分析[16]是将小波变换和相干分析相结合的一种分析方法,可以分析两列信号的相互依赖关系尤其可用于刻画模板与待测心电信号在不同频率点上的相关程度。
任意给定两段长度为N的信号x和y,分别实施连续小波变换得到其小波系数为CWTx(a,b)与CWTy(a,b)。进一步,采用交叉小波变换得到交叉小波谱WCSx,y(a,b)为
(2)
其中CWTy*(a,b)表示CWTy(a,b)的复共轭。基于此,可计算交叉小波相位角为
(3)
其中I和R分别代表交叉小波谱的虚部和实部,φxy∈[-π,π]。
为了更好地得到信号之间的同步信息,在计算小波相干值之前,我们需要对小波谱做平滑处理。定义平滑函数为
S(W)=Sa[St(W)]
(4)
其中Sa表示对尺度轴做平滑,St表示对时间轴作平滑,分别表示为
(5)
Sa(CWTx(a,b))=CWTx(a,b)*c2Π(0.6a)。
(6)
在式(5)中,c1是标准化系数,*代表卷积运算。在式(6)中,c2是标准化系数,Π是矩形函数,参数0.6是根据经验确定的尺度[17]。
在上述工作的基础上,信号x和y的小波相干值(wavelet coherence,WTC)定义为
WTCxy(a,b)=
(7)
1.2 阵发性房颤的自动检测
1.2.1 预处理 心电信号是一种非平稳信号,在采集过程中容易受到各种背景噪声的影响(主要包括工频干扰、肌电干扰和基线漂移等)。本文首先采用FIR数字滤波器[18]去除心电信号中的基线漂移;其次,采用小波变换[19]对原始心电信号进行分解并对高频系数进行软阈值处理;最后通过小波重构得到去噪后干净的心电信号。图3显示了一段心电信号(时长10s)去噪前后的效果。将去噪之后的心电信号进行无重叠的分段处理,分段后每个心电片段长度为10s(2500个采样点),并从数据集中随机选取一段10s正常心电片段作为模板。
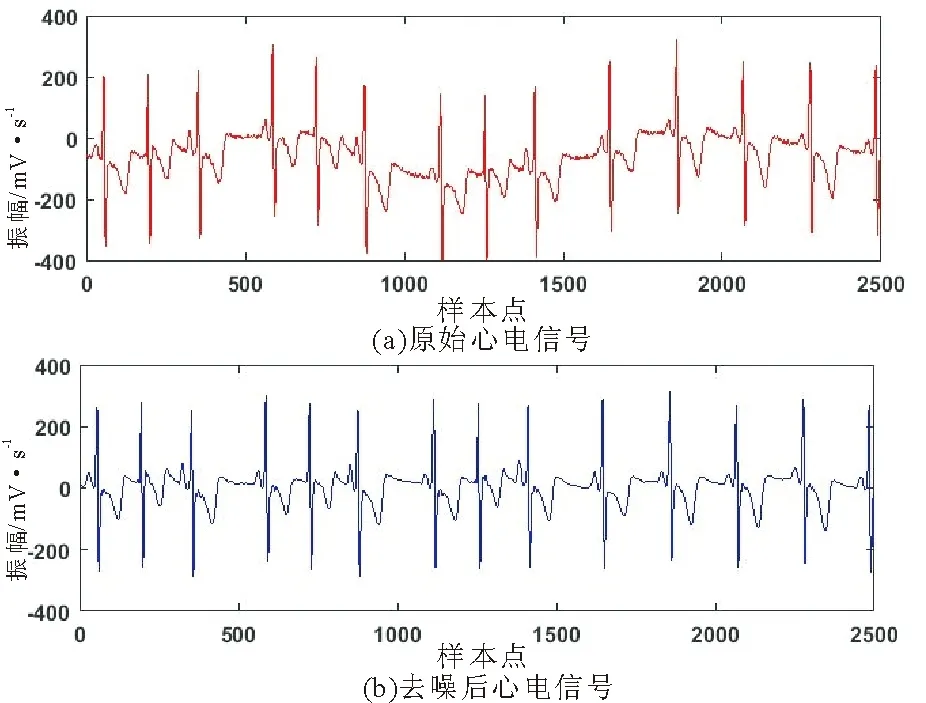
图3 心电信号去噪效果Fig.3 Thedenoising performance of ECG
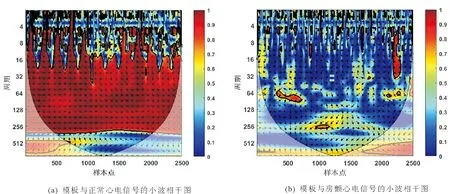
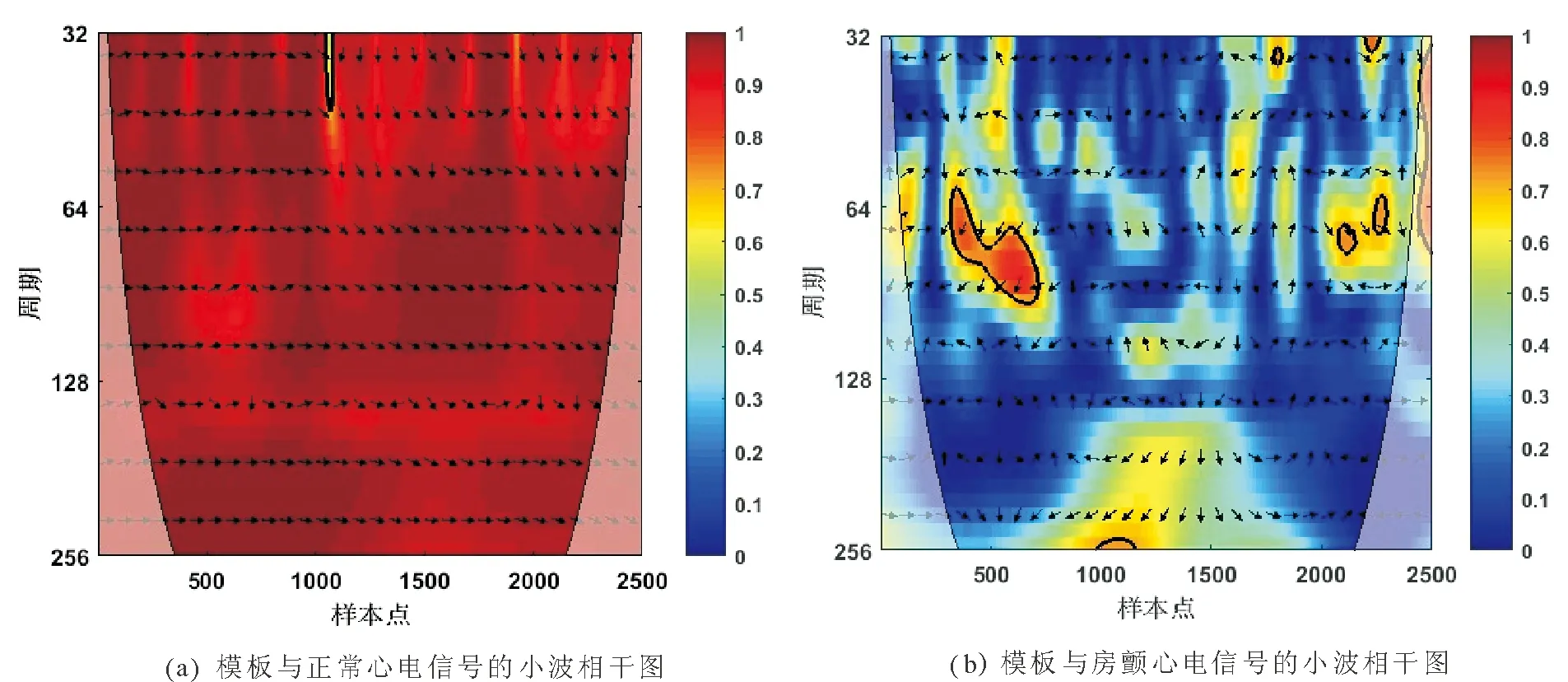
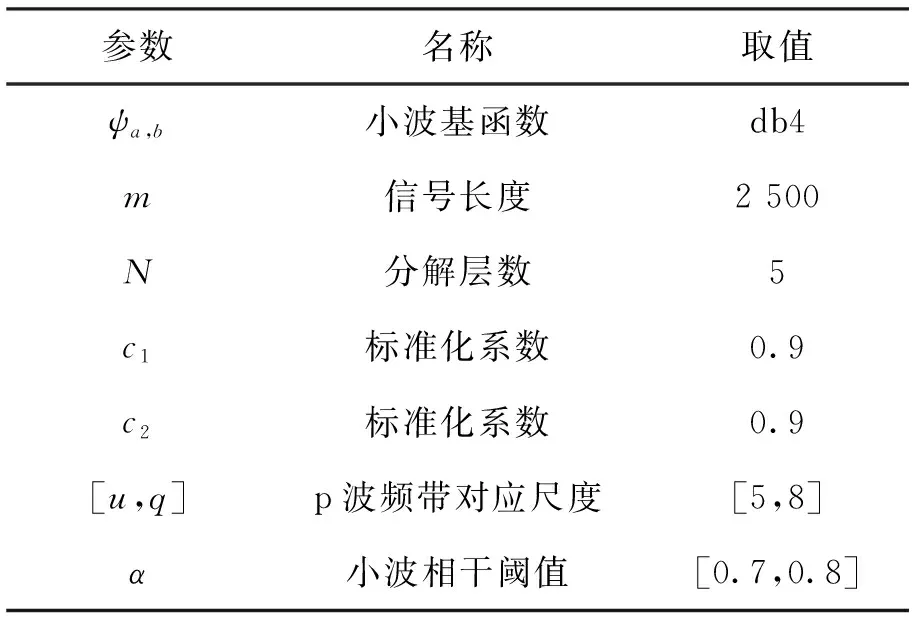
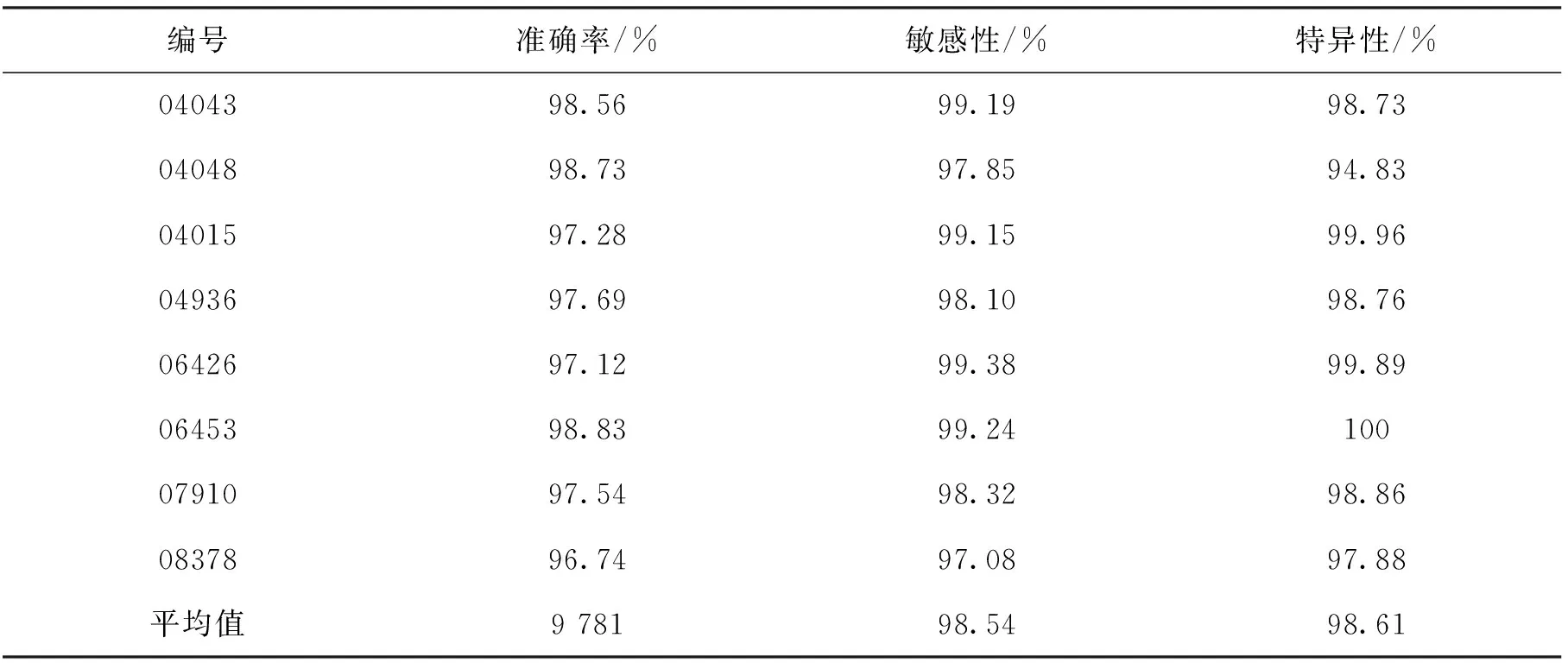
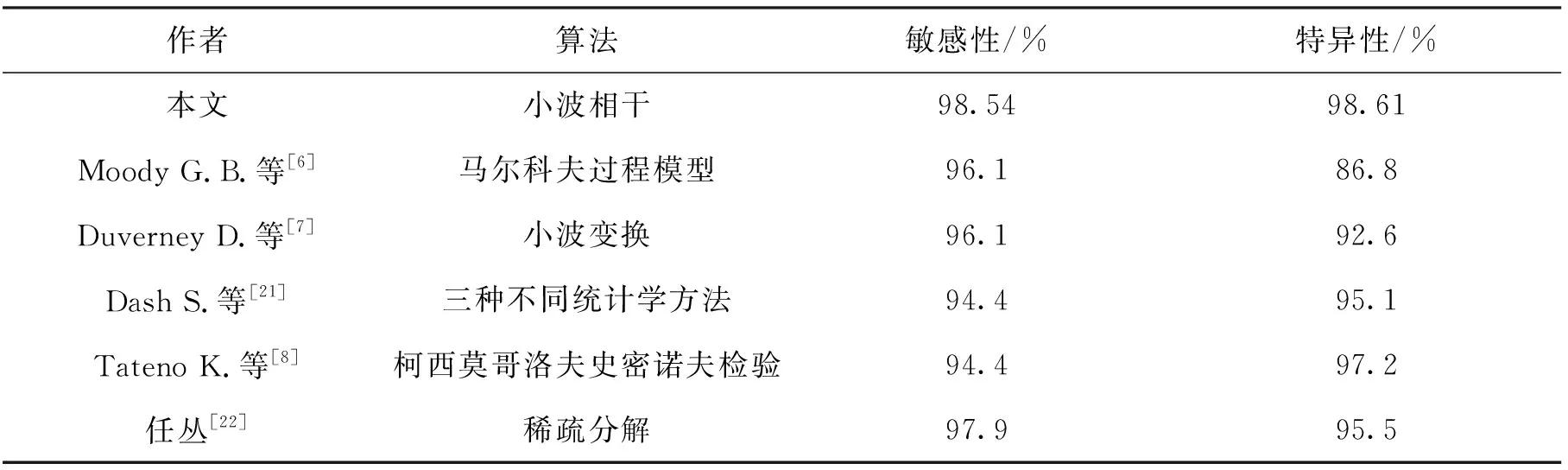
1.2.2 特征提取 给定模板心电片段Y={y(1),y(2),…,y(m)},并设X={x(1),x(2),…,x(n)}为待测心电信号,其中m,n表示信号长度且m 房颤发作时P波缺失而代之以f波(房颤波),且P波与f波重叠的频带范围一致。因此,可以提取并分析P波所在尺度上的小波相干图,如图5所示。其中,图5(a)是模板与正常心电信号的小波相干图,图5(b)是模板与异常心电信号的小波相干图。图中色标代表小波相干值,黑色箭头表示交叉小波相位角,这里仅标出了WTC≥0.5时的交叉小波相位角。从图5可以看出,相比于正常心电与模板匹配的小波相干图,房颤心电与模板匹配的小波相干值整体接近于0,且交叉小波相位角分布较为分散。基于此,本文采用3个度量指标来刻画上述差异,并将其作为所提取的房颤心电特征。具体步骤可总结为如下算法。 算法1(房颤心电特征提取方法) 给定心电信号X。 步骤2采用小波多尺度分析技术分别对Y和Xi进行连续小波变换,得到各自r到t层的低频小波系数,并根据公式(2)和(3)分别计算Y和Xi之间的交叉小波谱WCSXi,Y(a,b)和交叉小波相位角φXiY。记交叉小波相位角为 步骤3利用平滑函数S对交叉小波谱做平滑处理,进而得到小波相干值WTCXiY(a,b),记为 步骤4分别以样本点与周期为x轴与y轴,小波相干值为坐标(x,y)处的值,绘制模板与待测心电信号的小波相干图。 为心电信号X的房颤心电特征。 1.2.3 超限学习机 超限学习机(extreme learning machine,ELM)是2006年由Huang等人提出的一种新的学习算法[20]。原始ELM算法针对单隐层前馈神经网络,输入层与隐层的连接权重和阈值随机选取,采用可微或不可微的激活函数。与其他学习算法相比,ELM学习速度快、泛化精度高,且不易陷入局部最小值。 图4 待测信号与模板匹配对应的小波相干图Fig.4 The wavelet coherence map sbetween the template EEG and the present EEG 图5 特定尺度下待测信号与模板匹配对应的小波相干图Fig.5 The wavelet coherence maps between the template EEG and the present EEGat specific scales (8) 这里wj=[w1j,w2j,…,wnj]T是连接输入层与第j个隐单元的权值向量,bj是第j个隐单元的阈值,βj=[βj1,βj2,…,βjm]T是连接第j个隐单元与输出层的权值向量;wj·xi表示wj与xi的内积。假设网络中的实际输出与期望输出相同,则网络的学习过程即为求解到如下线性方程组: Hβ=T。 (9) 这里,H,β,T的定义如下: H= (10) β=[β1,β2,…,βL]T,T=[t1,t2,…,tN]T。 (11) 本文采用MIT-BIH心房颤动数据集[6],该数据集包括25个时长为1h的心电图记录,采样率250Hz,分辨率12-bit。本文从中随机选取8个心电记录进行数值实验,所有实验均在Matlab R2016中运行。 数值实验中,所有数据被随机均分为训练集和测试集。实验执行50次并取其平均结果作为最终分类性能的度量。 在特征提取过程中,首先对心电信号进行等长分段处理,每段心电数据长10s(2500个点),并做连续小波变换。正常与房颤心电图中最大区别在于P波缺失代之以f波(房颤波),且P波、f波重叠的频带范围为3~12Hz,故在小波相干图对应的P波尺度范围内进行特征提取。由于存在个体差异性,且模板的选择具有一定随机性,不适用于所有心电信号,因此根据临床验证对α进行取值。 表1 参数选取表Tab.1 Parameter selection table 首先,验证小波相干值的均值、比率、交叉小波相位角方差这3个单一特征的有效性与可行性,图6展示上述3个特征的箱线图。由图6可见,房颤心电的小波相干值均值和比率低于正常心电的对应值,房颤心电的交叉小波相位角方差高于正常心电的对应值,且均无异常值。这说明本文所提取特征可以有效区分正常心电与房颤心电模式。 其次,采用交叉验证来验证所提自动检测算法的可行性与有效性。在所选取的8个心电记录中随机选择7个作为训练集,剩余1个作为测试集。以此类推,最终取8组实验结果的平均值作为最终分类结果。表2列出了每组实验的准确率、特异性和敏感性以及平均值。从表中可以看出,本文所提算法具有优良的分类性能。 图6 本文所提取特征的箱线图Fig.6 The boxplot of the wavelet coherence analysis 编号准确率/%敏感性/%特异性/% 0404398.5699.1998.730404898.7397.8594.830401597.2899.1599.96 0493697.6998.1098.76 0642697.1299.3899.89 0645398.8399.241000791097.5498.3298.860837896.7497.0897.88 平均值9 78198.5498.61 表3 本文所提方法与已有方法的检测性能比较Tab.3 Performance comparison between the proposed method and some existing methods 最后,将本文所提算法与已有算法进行比较(见表3)。从表中可以看出,本文所提算法的平均敏感性及特异性达到SE=98.54%及SP=98.61%,均高于其他算法。 本文提出了一种基于小波相干分析的阵发性房颤自动检测方法。首先,对所有的心电信号进行预处理,包括去除噪声、分段处理、选取模板等;其次,对模板与待测心电信号进行小波相干分析得到小波相干图;进而,计算小波相干值的均值、比率以及相位角方差,构成房颤心电特征;最后,将所提取特征结合超限学习机完成阵发性房颤的自动检测。本文采用MIT-BIH心房颤动数据库进行数值实验,实验结果表明,本文所提算法具有良好的检测性能,可以为临床诊治提供一定的辅助作用。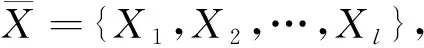
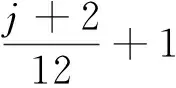
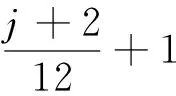
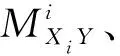
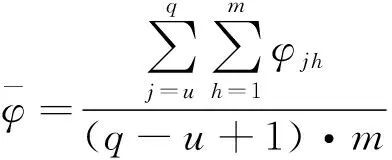
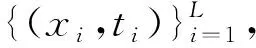
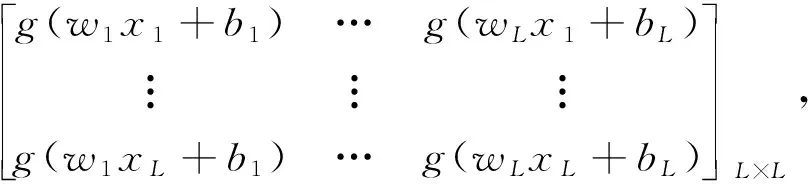
2 数值实验结果与分析
2.1 心电数据
2.2 结果与分析

3 结 语
