兰州市交通拥堵研究

汤旻安,王攀琦

(1.兰州交通大学 自动化与电气工程学院, 甘肃 兰州 730070;2.兰州理工大学 机电工程学院,兰州 730050)

城市化与机动化发展水平的提高,对整个交通运输的格局产生了根本性的改造。然而,城市交通供求矛盾的情况也日渐凸显,道路交通拥堵情况逐渐加剧。道路拥堵带来了交通管理矛盾突出、环境污染、能源消耗显著以及应对突发事件的响应时间延长等城市综合问题。

兰州市属于典型的河谷地形,这种地形条件下城市交通路网的形成受到严重的制约。整个市区呈一字型分布,城区的划分也根据这一地形进行功能分区。黄河穿过城市中心,将市区分为南北两个部分,东西方向的主干道承载了兰州市交通的大部分客流,而南北方向则不够通达,其交通状况整体表现为东西交通量大,南北闭塞的局面。除了两山夹黄河的天然屏障,近年来机动车的增加也是一个不容忽视的影响因素。除了上述这些原因,铁路对兰州市路网的二次分割加剧了交通拥堵现状[1-2]。

图1 兰州市地形图Fig.1 Lanzhou topographic map

城市交通拥堵问题是一个复杂的系统性问题,对其进行研究具有巨大的现实意义[3]。本文挖掘兰州市交通评价体系中交通的参数,利用因子分析法(FA)和聚类分析对兰州市交通拥堵状况进行评价。首先,利用因子分析方法对交通量各参数提取公共因子,其次,利用聚类分析发掘各路口的相关性。除此之外,利用主成分分析法在保证数据完整性的条件下对各项参数降维,将其数据分析结果与因子分析的数据处理结果进行对比,进行综合分析验证。Wen等人指出,缓解交通拥堵的基本原则是科学定量地描述交通拥堵[4]。本研究通过综合运用因子分析和聚类分析进行理论探索和实证分析,对兰州市交通拥堵状况作出了合理的评价，将为地方政府的交通管理提供科学的决策方法。

1 因子分析法

因子分析是一种多元统计分析技术,在解决多变量问题时,具有显著的优点,其主要思想是将原始的变量进行分组,得到每组变量的相关性,从新得到的n组变量中提取出新的公共因子,可以同时处理许多因素相互影响的复杂体系[5]。正是这些特性,使得它在特征提取、数据压缩方面都有着广泛的应用。造成交通拥堵影响的因素有很多,用因子分析对各个因素的数据进行规格化处理,发掘造成兰州市交通拥堵的潜在因素。

设对兰州交通有影响的因素数目为N,选取路口数目为M,则原始数据矩阵为

(1)

xij为第i个路口第j个指标的观察数据,i=1,2,…，M；j=1,2,…,N。

因子分析中每一个变量用新公共因子的线性函数与特殊因子之和表示,公式为

Xi=ai1F1+ai2F2+…+aimFm+εi,

(i=1,2,…，p)

(2)

其中,F1,F2,…，Fm为求取的新的公共因子,εi为特殊因子。

此模型用矩阵表示为

X=AF+ε。

其中,

(3)

矩阵A称为因子载荷矩阵,aij称为因子载荷。

因子分析的计算从协方差矩阵入手,可以证明,经过标准化处理后的数据的协方差矩阵就是X的相关系数矩阵。因此,可以直接利用上文主成分分析得到的相关系数矩阵进行分析。

求解因子载荷阵的具体方法如下:

1)计算标准化处理后的数据的相关系数矩阵,并通过相关显著性检验方法检测因子分析法对所取样本数据的适用性。

2)计算相关系数矩阵的特征根及其对应的特征向量,根据特征值的大小(一般取大于1的特征值)和累积方差贡献率(累积贡献率达80%以上)来确定因子个数。

3)利用相关系数矩阵的特征根和特征向量计算因子载荷矩阵，

(4)

因子分析法的目的是为了减少变量个数,实现降维,因此,得到的公因子数目是小于变量数目p的。

由因子载荷矩阵可知,因子载荷矩阵第j列元素的平方和

(5)

又因为第j列元素的平方和为

(6)

所以有λj=gj2,各个因子的方差贡献gj2即是其对应的各第j个特征根。

确定要提取的因子即是选取方差贡献大于1的因子,也可以利用累积方差贡献率来确定要提取的因子的个数m。

4)计算因子得分系数[6-7]。

2 聚类分析

聚类分析用来分析衡量同类样本的类似性,即将高维空间数分布的结构特征用二维图像显示,利用对二维图像的识别能力考察高维空间数据分布结构的特征。利用这一特性,从各路口的历史数据中获得路口间交通流量的相似性和相关性,找出各路口间的相互关系[8]。对高维数据点Xi(xi1,xi2,…,xim),其二维显示的对应点为Yi(yi1,yi2),则yi1,yi2应是xi1,xi2,…,xim的某种函数。这里采用非线性映射方法(NLM)得到二维图像。根据NLM方法,多维空间中的点经过投影后，点与点之间的距离必然会产生误差。

在m维空间，矢量Xi和Xj的距离为

(7)

在二维空间中,矢量Yi和Yj的距离为

dij=dis(Yi,Yj)。

(8)

映射时的误差函数为

(9)

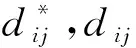
3 数据获取与处理

交通拥堵的原因是多方面的,从不同的角度都可以对其进行评价。道路交通拥堵评价指标可分为交叉口指标、路段指标、区域指标,城市交叉口作为路网的节点和交通的咽喉,对于一个城市交通状况的评估和改善有着重要的意义,本文选择交叉口指标来进行研究[11]。

3.1 数据的获取

交通量不是一个静止量,随时处于变动之中,但其变化具有统计规律性。在调查时,每个路口的4个方向都要设置调查组。调查时为了使数据更有说服力,需要对相对拥堵的多个路口都进行测量统计,最终再从其中几个路口进行研究分析。

为了对兰州市交通拥堵的主要原因进行分析,选取了8个交叉路口及其交通量参数:机动车量、非机动车量、引道延误、车速、路段均速、效率指数、饱和度等。车速是衡量道路通行能力的重要参数。车辆在区段行驶时,往往受到各种因素的影响,如道路线形、车行道宽度、路面状况、车辆性能、停靠站位置、交叉口交通状况及气候条件等。

3.2 数据整合

在交通量的测量中,需要将不同类型车辆换算成标准车辆,然后进行汇总，换算系数如表1所示。

获取数据时,由于观测或者记录的原因,可能会导致有些数据明显不合理,在实际分析中要淘汰这些数据。在分析中如果出现了参数未按要求记录、延误时间为负、明显地超过了合理范围等情况就认为数据失效。因此,必须对无效数据进行剔除。

除此之外,在实际的提取数据的过程中,不可避免地会存在设备故障、操作失误而造成的个别数据丢失。这时需要对丢失的数据进行弥补，常用的技术就是均值弥补,即用集中变量的均值来代替丢失的数据。还可能有个别数据离群较远,或者叫作异常值、极端值，一般情况下,这种数据应直接舍去。

从兰州市主要的拥堵路口路段中选取一些具有代表性的路口进行分析。通过实地检测,选取8个路口,得到各交通流信息如表2所示。

表1 标准车换算系数Tab.1 Conversion coefficient of standard vehicle

数据来源:兰州市交通规划调查报告

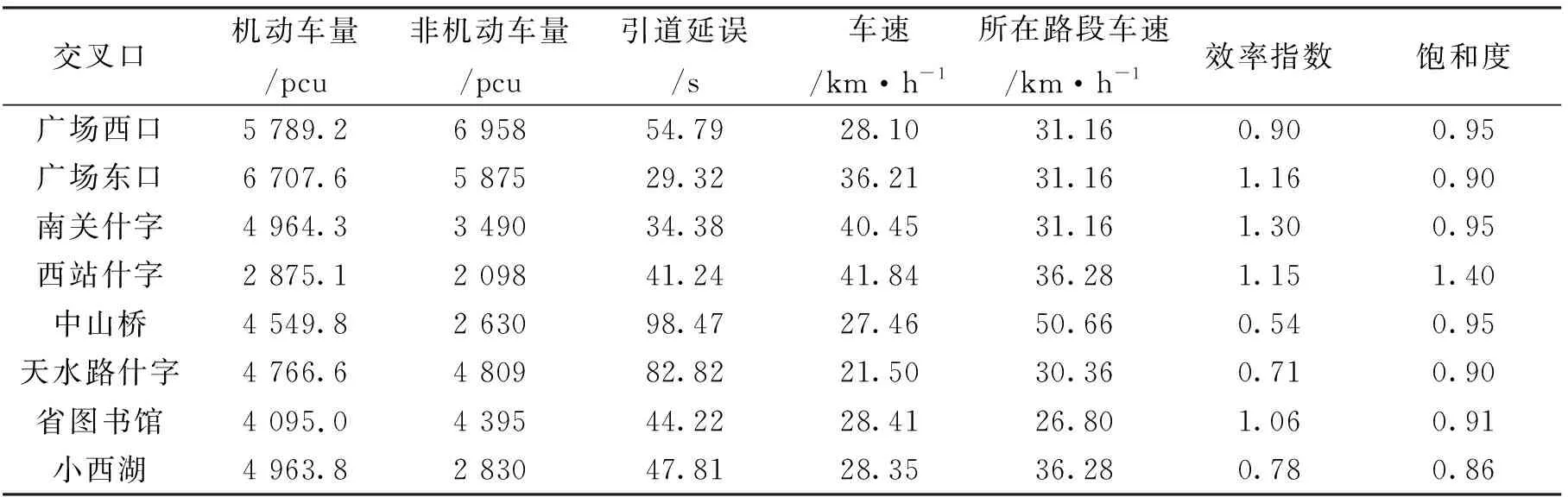
表2 兰州各路口交通参数值Tab.2 Traffic parameters of each intersection in Lanzhou

数据来源:兰州市交通规划调查报告。

4 仿真结果分析

4.1 因子分析结果

本文采用SPSS软件进行因子模型分析[12],进行因子分析的7个指标:机动车量(B1)、非机动车量(B2)、引道延误(B3)、车速(B4)、路段均速(B5)、效率指数(B6)、饱和度(B7)。

经计算得到相关系数矩阵及相关显著性检验如表3所示。上下两部分分别为原始变量相关系数矩阵和相关系数显著性检验的P值,从上半部分可以看出,矩阵中存在大量高值相关系数,下半部分P值存在很多小于0.05的数值,上下两部分均表明原始变量之间存在着较强的相关性。

表3 相关系数矩阵及相关显著性检验Tab.3 Correlation matrix and relevant significance test

表4为特征根及方差贡献情况。初始特征值用于选择和确定要提取的因子,共有3项,分别为特征值、方差贡献率、累积方差贡献率。在表4中共有两个因子的特征根大于1,所以应提取两个因子，如表5所示。从旋转前因子方差贡献率可以看到,提取出的两个因子可以解释原始变量81.383% 的信息,具有代表性。对比旋转前后方差贡献情况可以看出,旋转后两个因子的特征根和方差发生改变,但其累积方差贡献率与旋转前保持一致。

表4 特征根与方差贡献Tab.4 Characteristic root and variance contribution

因子旋转的目的在于使因子载荷简单化,便于对测量数据点进行分组。从表5可看出,两个因子在不同原始变量上的载荷范围没有明显的差别,因此要对因子载荷进行旋转。

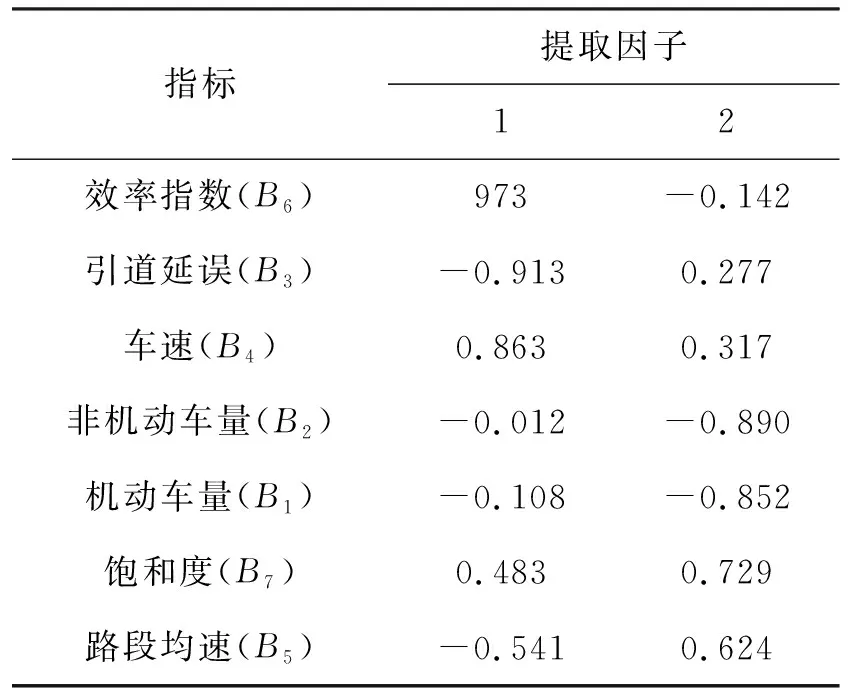
表5 旋转前因子载荷阵Tab.5 Factor load array before rotation

从表6可以看出,旋转后载荷系数两极差异显著。第一公因子在指标B6(效率指数)、B3(引道延误)、B4(车速)、B5(路段均速)上有较大载荷,这表明这些指标有较强的相关性,归为一类,从影响因素来看,这些指标主要受道路条件的制约,对于兰州,对道路限制最大的是两山夹一河的特殊地形,因此可以把第一公因子命名为“地形因子”。第二公因子在B1(机动车量)、B2(非机动车量)、B7(饱和度)上有较大载荷,而这3个因子都是关于交通量的指标,因此,可以将其命名为“交通量因子”。

从相关系数矩阵出发来进行因子分析,这里的B1～B7是标准化变换之后的变量。此外,因子得分是利用旋转后的因子载荷阵得到的。根据因子分析的数学特性可以得出,得分值越大的因子,其对新因子的影响也越大[13]。从表7和图2可以看出, 7个指标中， 3(引道延误)、 4(车速)、 5(路段均速)、6(效率指数)与地形关系较大,1(机动车量)、2(非机动车量)、7(饱和度)与交通量关系较大。

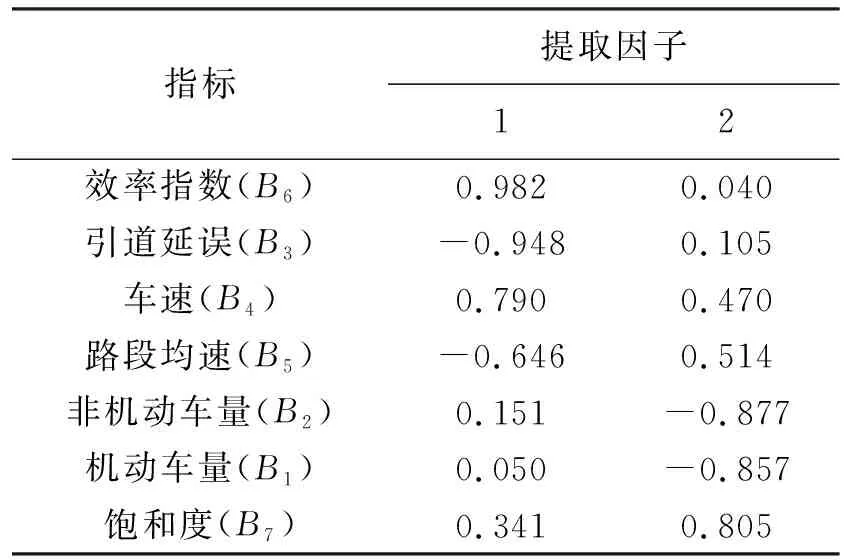
表6 旋转后因子载荷阵Tab.6 Factor load array after rotation

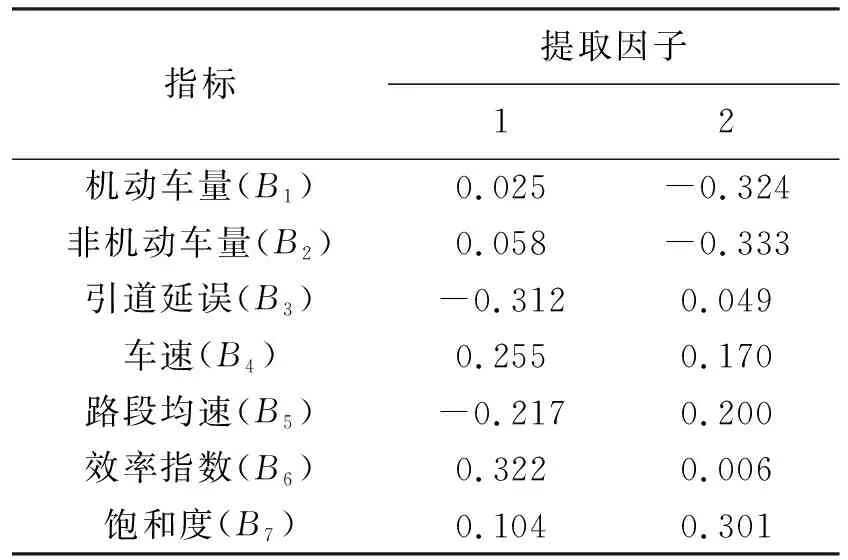
表7 因子得分系数矩阵Tab.7 Component score coefficient matrix

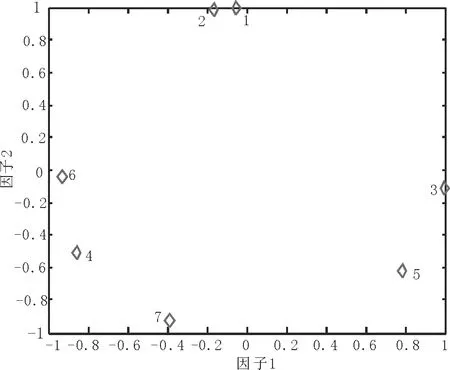
图2 各因子得分图Fig.2 Score of each factor

通过图3可以看出，各交通路口联系的紧密程度,南关什字 (3)、中山桥 (5)、小西湖(8)的3个路口数据在二维空间的距离比较接近,说明这3个路口之间的联系较为紧密。同样得出,天水路什字(6)和省图书馆(7)两路口关系较大。各路口的分类在二维平面图上是按照一定的方向和顺序邻次排列的,自右向左,拥堵程度逐渐增加。因此,各个路口之间不是相互独立的,反而有着一定的联系。不同的拥堵类别,客观地反映了地理、车流对交通状况的影响。在对交通流进行控制和疏导时,对于联系紧密程度不同的路口,应分别考虑各路口之间的相互影响,以便实现合理疏导。

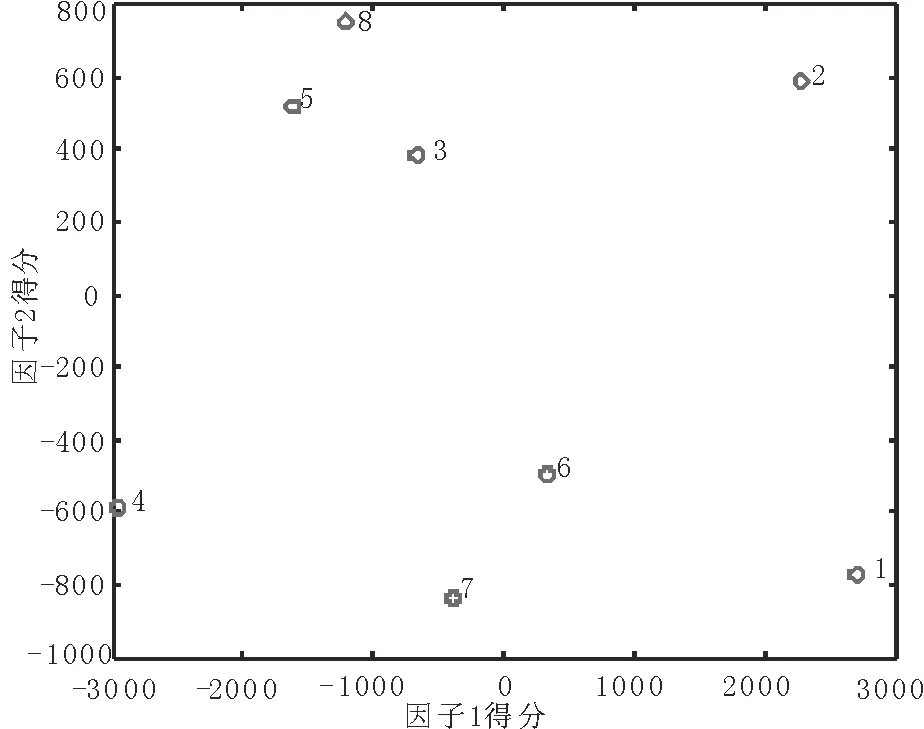
图3 高维数据映射到二维空间的结果图像Fig.3 High-dimensional data is mapped to the result image in two-dimensional space

4.2 主成分分析与因子分析的对比

PCA是一种多元统计分析技术。它是一种基于目标统计特性的正交变换方法,变换后的新分量正交或不相关,同时可以反映原始变量的绝大部分信息[14]。分析结果如图4所示。

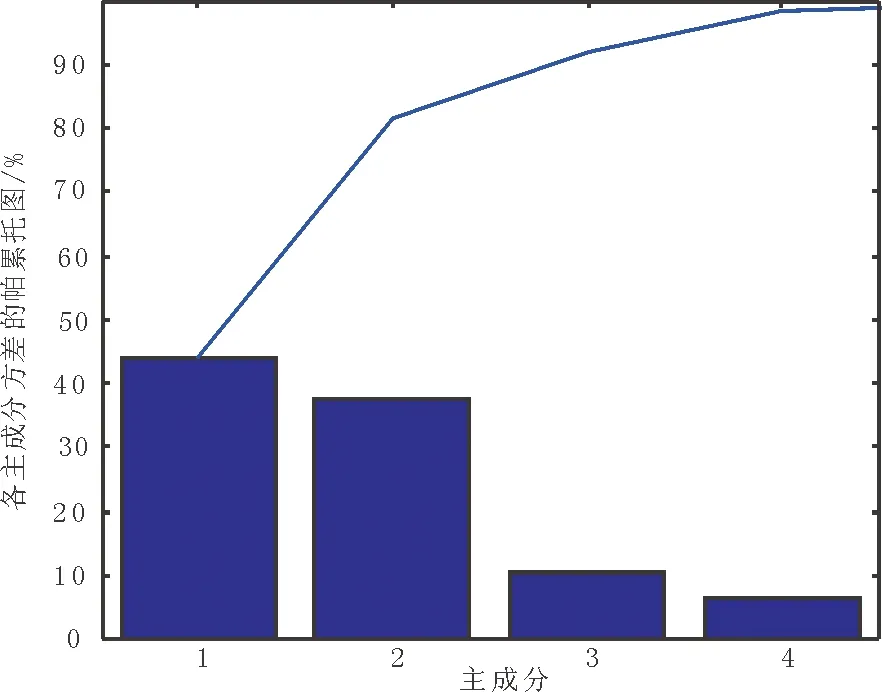
图4 各主成分方差的帕累托图Fig.4 Pareto charts for variance of the principal components

通过图4可以简明地看出，各个新主成分的各自贡献率及其对应的累积贡献率的大小,选取前3个成分：机动车量(1)、非机动车量(2)、引道延误(3),其累积贡献率为91.763 5%(大于85%),因而前3个主成分即可作为提取的主成分,来代表全部7个变量的大部分信息。根据前3个主成分得分,用其贡献率加权,可分别求出8个路口各自的得分[15]。

运用PCA仿真分析得到,造成兰州市交通拥堵的主要原因包括机动车和非机动车交通量过大，混合交通流量往往会加剧交通的拥堵。由于受自行车和行人影响,机动车减速、停车等待、占用路面等问题总是导致道路堵塞。因此,与机动车交通流量相比, 混合交通流量加重了交通拥堵[16]。其次,引道延误方差贡献率也较大,而道路条件是对引道延误的主要制约因素,说明兰州市的特殊地形同样是交通拥堵的巨大诱因。

综上所述,兰州市的道路条件,即河谷狭长地形以及车流量是导致兰州市交通拥堵现状的首要因素,与因子分析提取出的两个新因子“地形”、“交通流”的结论是一致的,因此把二者视作拥堵治理的重点对象。

5 结 语

本文综合运用了因子分析法和聚类分析对兰州交通拥堵状况进行了分析。首先，利用因子分析法建立因子分析模型,提取出不可观测的潜在变量,分别为车量因子和地形因子。然后，利用聚类分析对8个交叉口进行分类,分析了路口之间的相关性。最后，运用主成分分析法提取主成分,与因子分析进行对比。运用PCA 法提取出了机动车量、非机动车量、引道延误这3个新主成分。这一仿真结果证实了因子分析结果的正确性。可以证明,二者分析结果一致,因此，总结兰州市交通拥堵的主要因素为兰州市特殊的地形和混合交通量。本文的研究结果为兰州市交通拥堵治理提供了明确的方向。此外,还可以把路段和交叉口各个交通量结合在一起同时进行因子分析,这将对兰州市交通拥堵的缓解和治理有重要的指导意义。