全国高考数学解答题答题规范及得分要领系列讲座（2）

■北京市第十二中学 高慧明

一、离散型随机变量的分布列

例12015年,我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖。以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法。目前,国内青蒿人工种植发展迅速。调查表明,人工种植的青蒿的长势与海拔、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定人工种植的青蒿的长势等级:若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级。为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到表1中的结果:

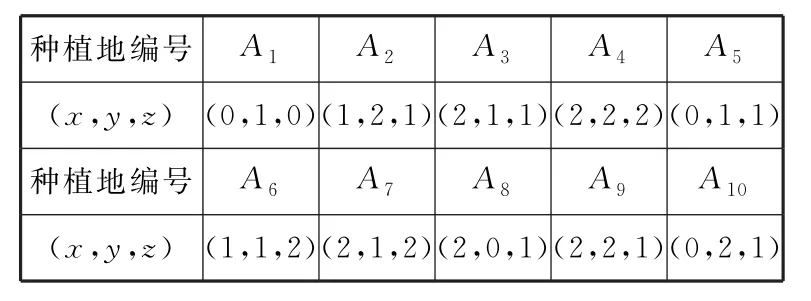
表1

(1)在这10块青蒿人工种植地中任取两地,求这两地的空气湿度指标z相同的概率;

(2)从长势等级是一级的人工种植地中任取一块,其综合指标为m,从长势等级不是一级的人工种植地中任取一块,其综合指标为n,记随机变量X=m-n,求X的分布列与数学期望。

审题思路：(1)对事件进行分解→求出从10块地中任取两块的方法总数→求出空气湿度指标相同的方法总数→利用古典概型求概率。

(2)确定随机变量X的所有取值→计算X取各个值的概率→写分布列→求期望。

规范解答：(1)由表可知:空气湿度指标为0的有A1;空气湿度指标为1的有A2,A3,A5,A8,A9,A10;空气湿度指标为2的有A4,A6,A7。所以空气湿度指标z相同的概率为

(2)计算10块青蒿人工种植地的综合指标,可得表2:

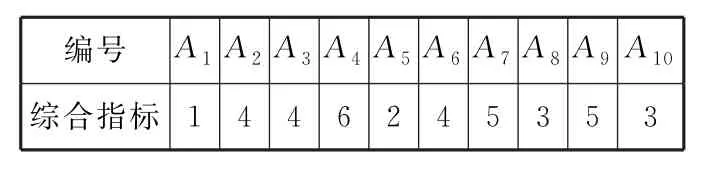
表2

其中长势等级是一级的(ω≥4)有A2,A3,A4,A6,A7,A9,共6个,长势等级不是一级的(ω＜4)有A1,A5,A8,A10,共4个。

所以X的分布列为表3:

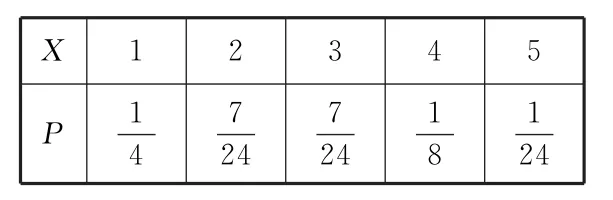
表3

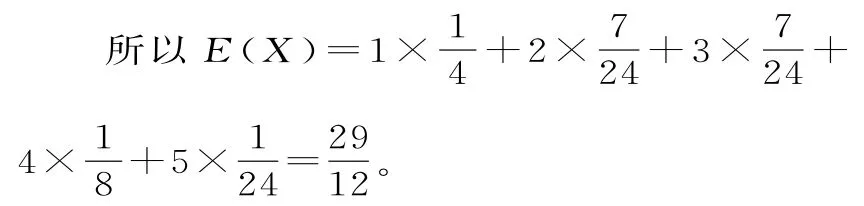
答题模板：第一步,定元:根据已知条件确定离散型随机变量的取值。

第二步,定性:明确每个随机变量取值所对应的事件。

第三步,定型:确定事件的概率模型和计算公式。

第四步,计算:计算随机变量取每一个值的概率。

第五步,列表:列出分布列。

第六步,求解:根据公式求数学期望。

评分细则：(1)列出空气湿度相同的情况给2分;计算概率时只要式子正确给2分。

(2)列出长势等级的给2分,只要结果正确无过程的也不扣分;计算概率的式子正确给3分;正确写出分布列给1分。

二、直线与圆锥曲线的位置关系

例2在平面直角坐标系x O y中,已知椭圆的离心率为在椭圆C上。

(1)求椭圆C的方程。

审题思路：(1)由椭圆C上的点满足条件→得到a,b的关系式用基本量法求得椭圆C的方程。

规范解答：(1)由题意知又,解得a2=4,b2=1。所以椭圆C的方程为

②设A(x1,y1),B(x2,y2)。

将y=k x+m代入椭圆E的方程,可得(1+4k2)x2+8k m x+4m2-16=0。

因为直线y=k x+m与y轴交点的坐标为(0,m),所以

答题模板：第一步,求圆锥曲线方程:根据基本量法确定圆锥曲线的方程。

第二步,联立消元:将直线方程和圆锥曲线方程联立得到方程A x2+B x+C=0,然后研究判别式,利用根与系数的关系。

第三步,找关系:从题设中寻求变量的等量或不等关系。

第四步,建函数:对于范围最值类问题,要建立关于目标变量的函数关系。

第五步,得范围:通过求解函数值域或解不等式得到目标变量的范围或最值,要注意变量条件的制约,检查最值取得的条件。

评分细则：(1)由a2-c2=b2直接得b=1,扣1分。

三、解析几何中的探索性问题

例3已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点。

审题思路：(Ⅰ)设A B的方程y=k(x+1)→利用待定系数法求k→写出方程。

规范解答：(Ⅰ)依题意知直线A B的斜率存在,设直线A B的方程为y=k(x+1),将y=k(x+1)代入x2+3y2=5,消去y整理得(3k2+1)x2+6k2x+3k2-5=0。

设A(x1,y1),B(x2,y2),由题意可知

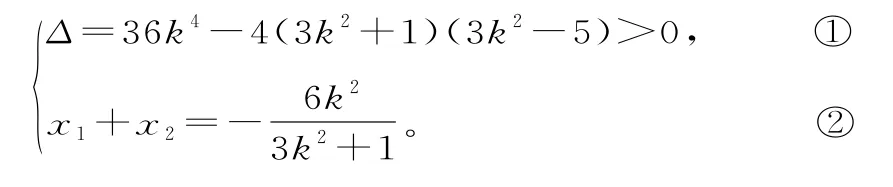
(2)当直线A B与x轴垂直时,此时点A,B的坐标分别为当

答题模板：第一步,先假定:假设结论成立。

第二步,再推理:以假设结论成立为条件,进行推理求解。

第三步,下结论:若推出合理结果,经验证成立则肯定假设;若推出矛盾则否定假设。

第四步,再回顾:查看关键点,易错点(特殊情况、隐含条件等),审视解题规范性。

评分细则：(1)不考虑直线A B斜率不存在的情况扣1分。

(2)不验证Δ＞0,扣1分。

(3)直线A B的方程写成斜截式同样给分。

(4)没有假设存在点M不扣分。