基于分数布朗运动和随机利率下两值期权定价

邓婷婷，韦才敏

（汕头大学数学系，广东 汕头 515063）

0 引言

金融衍生品定价问题一直是数理金融的核心内容之一.期权作为股票的衍生产品，很多学者对其定价问题进行了深入的研究.自从1973年著名的B-S期权定价模型及其定价公式提出后，有关期权定价理论及应用得到了迅速的发展.由于经典的B-S模型是在理想的假设条件下得到的，因此并不符合实际的金融市场.由于分数布朗运动具有自相似性和长程依赖性等特性，在金融市场模型中用分数布朗运动取代标准布朗运动早已经被众多学者认可.这与人们对金融市场的直观感觉一致，使得其成为了描述标的资产价格过程的一个有力工具.关于分数布朗运动的最早研究成果可追溯到Kohnogorov，并命名为Wiener螺线[1].Mandelbrot和Van Ness[2]首次提出了分数布朗运动.Decreusefond等人[3]阐述了分数布朗运动相关理论与应用.Carmona等人[4]给出了分数布朗运动的随机积分.Elliot和Hoke[5]研究了在Hurst指数在H∈（0.5,1）情况下的分数布朗运动，通过Wick积分的方法得到了Girsanov定理和分数Itô公式.Necula[6]分析了在分数布朗运动环境下的期权定价.

利率是影响金融市场变化的最基本的因子.市场利率在短期情况下，一般可被认为是稳定的，可看作是常数.但在长期情况下，由于经济发展状况、股市的起伏以及国家政策等因素都会引起市场利率的波动，因而，利率是一个随时不断变化的量.很多研究者开始对经典的B-S定价模型进行改进，使其更符合实际情况.Kim[7]研究了随机利率下的期权定价问题，得到了其定价公式，并在此基础上进行了相关的实证分析.Zhang等[8]人研究了基于随机利率投资策略的看涨期权定价.康文娟和李翠香[10]研究了标的资产服从几何布朗运动，利率服从Vasicek模型，用多维Girsanov定理和测度变换推导出相关性数字期权的定价公式.张娟和金志明[11]在随机利率的基础上运用鞅方法推导出欧式期权价值过程所满足的微分方程.李康乐[12]通过市场历史数据对MHL，Vas，CIR和BrS四种随机利率下的期权定价模型进行了统计分析，得到了随机利率对期权定价影响的实证分析结果.许聪聪[13]主要致力于期权定价问题的研究，运用鞅论、随机分析等现代数学工具研究随机利率模型下的期权定价问题，并得到了相应定价公式.

此外，与标准的交易所交易的期权相比，仍存在着以满足市场特殊要求的新型期权产品，有时它们被附加在所发行的债券中以增加对市场的吸引力.两值期权是一种具有不连续收益的新型期权，只有标的资产的价格超过执行价格才会有收益.目前关于两值期权的研究有：郭华英[14]探究了标的资产服从标准布朗运动和假定利率服从Hull-White随机利率的两值期权的定价问题.满圆圆[15]研究了在标的资产服从几何布朗运动下，运用Girsanov定理进行测度变换，再利用Bayes法则消除随机项，得到两值期权的定价公式.王海叶[16]推导了在无风险利率、股价波动率变化的市场模型中两值期权的定价公式.孙天宇和刘新平[17]利用对冲的思想和偏微分方法，研究了股票价格满足几何布朗运动情况下有交易成本和支付红利的两值期权定价问题.

本文在上述研究的基础上，将标准布朗运动的Vasicek随机利率模型下的两值期权问题推广到Hurst指数为H∈（0.5,1）的分数布朗运动Vasicek随机利率模型下的两值期权定价问题.利用偏微分方程的相关知识求解此模型，从而推导出两值期权的定价公式，期望能得到更贴近市场真实值的结果.

1 预备知识

两值期权（binary option）是由合同条款变化而产生的新型期权，具有不连续收益的特点，其收益与期权为实值状态时的盈利程度无关[18].即期权在到期日处于实值状态时，其收益为事先约定的固定数额；若处于虚值状态时，其收益为零.以两值看涨期权为例，它分为两种类型：

（1）现金或无值看涨期权（cash-or-nothing call）（简写为CONC）：在到期日股票价格低于敲定价格时，则期权价格为零；而当股票价格超过敲定价格时，则期权卖方将支付1元给期权买方.

（2）资产或无值看涨期权（asset-or-nothing call）（简写为AONC）：在到期日股票价格低于敲定价格时，则期权价格为零；而当股票价格超过敲定价格时，则期权卖方将按规定支付股价给期权买方.

引理1 在分数Vasicek随机利率模型下，假设 V＝V（St，rt，t）是一个关于 St，rt和t的三元函数，无风险利率rt满足以下随机微分方程

其中a，b，σr都是正常数，a表示利率的调节速度，b表示长期利率，σr表示即期利率的波动率.

风险资产股价遵循几何分数布朗运动

其中St表示 t时刻的股票价格，σ 表示股价波动率，是带有Hurst指数H（0＜H＜1）相关系数为ρ的分数布朗运动，并且满足

从而得到

证 根据Taylor展式得

由于

将上式及（1），（2）带入（4），得

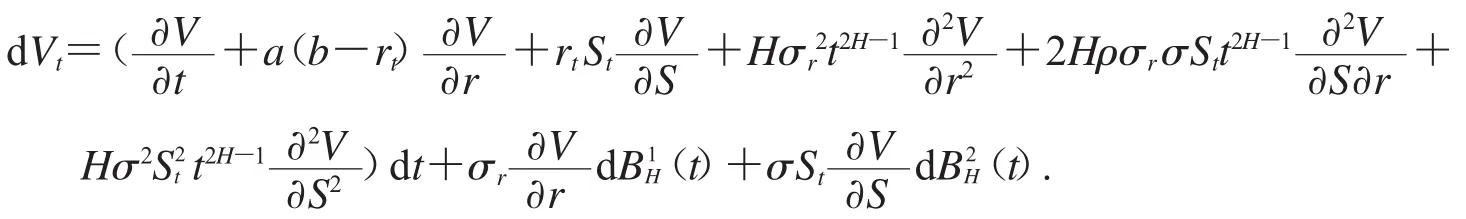
定义1.1[9]假设（Ω，F，P）是一个完备的概率空间，Hurst指数为H（0＜H＜1）的分数布朗运动 B（Ht）＝{B（Ht），t≥0}是一个连续的高斯过程，且满足：

（1）B（H0）＝E（B（Ht））＝0；

当 H＞0.5 时，B（Ht）具有长期相关性，即 r（n）＝E（B（H1））（BH（n＋1）－BH（n））＞0，并且.Hu和φksendal在H＞0.5时通过Wick积和分数白噪声理论证明了Itô型分数B-S市场无套利且完备的.

2 零息票债券定价

由于利率本身是不可交换的资产，所以在风险管理和衍生产品定价等研究中，用一种较为常见的金融工具—零息票债券作为利率的载体，因此想要对Vasicek随机利率下的分数布朗运动进行期权定价，首先给出零息票债券定价公式.

零息票债券是一种不支付利息的债券，通常在到期日按面值支付给债券持有者.以P（t，T）表示在t时刻零息票债券的价值.不失一般性，假设零息票债券是一张在到期日T时换取1元现金的债券，即P（T；T）＝1.由于在随机利率的假设下，零息票债券是时间和利率的函数，即P＝P（rt，t，T）.下面将利用风险对冲原理来计算t时刻零息票债券的价格 P（rt，t；T）.

2.1 零息票债券所满足的偏微分方程

引理2[19]在分数Vasicek随机利率模型下，到期日为T的零息票债券在t时刻的价格满足的偏微分方程为

2.2 零息票债券的定价公式

根据零息票债券所满足的偏微分方程（即引理2），可以得到零息票债券的定价公式.定理1在分数Vasicek随机利率模型下，到期日为T的零息票债券在t∈[0,T]时刻的价格为

其中

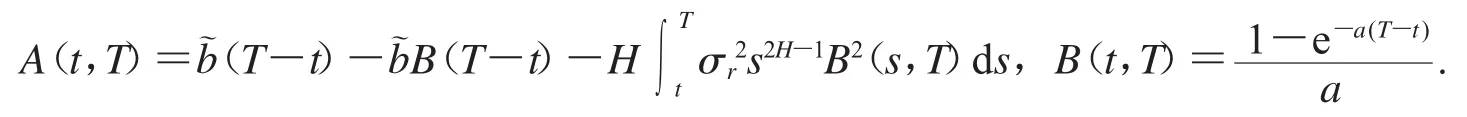
证明：根据利率的随机性和零息票债券是无风险的特点（dP＝rtPtdt），t时刻零息票债券的价值可以表示为

由（5）可得，零息票债券在t时刻的价格具有如下形式的解

且满足 A（T，T）＝0，B（T，T）＝0.

对（6）两边分别对t求一阶偏导，对r求一阶、二阶偏导可得

代入（5）并化简可得

有

从而定理得证.

3 分数布朗运动和Vasicek随机利率下的两值期权定价

3.1 基本假设

借助B-S模型的基本假设，给出如下假设：

1）市场上的资产是完全可分的，可进行连续交易，允许对资产进行卖空；

2）市场是完备的，所有未定权益可复制；

3）市场上的投资者可按无风险利率任意的借入和借出；

4）股票在期权生存期内不支付红利；

5）市场上不存在套利机会，且不存在税收和交易成本；

6）Δ－对冲原理构造投资组合的期望回报率等于无风险利率.

3.2 两值期权所满足的偏微分方程

引理3 在分数 Vasicek 随机利率模型下，t∈[0，T]时刻两值期权 Vt＝V（St，rt，t）所满足的偏微分方程为

证明：首先利用Δ－对冲原理构造投资组合，该投资组合由1份期权，Δ1t份股票和Δ2t份零息票债券构成，则在t时刻该投资组合的价值为

在[t，t＋dt]时间内，投资组合价值的变化为

由于投资组合在[t，t＋dt]时间内是无风险的，将（3）式以及零息票债券的微分代入上式，整理得

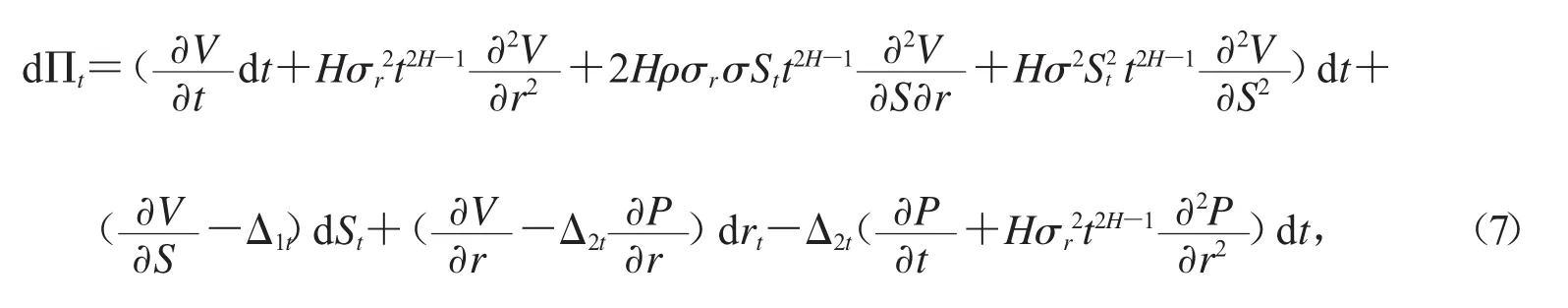
为了消除（7）式中的随机项，令

将上式代入（7）式，并注意到（5）式，得

由于投资组合是无风险的，则根据无套利原理得

联立（8）和（9）式可得

在到期日t＝T时，有

从而引理3得证.

3.2.1 现金或无值期权的定价公式

根据引理3，对现金或无值看涨期权（CONC）进行定价.

定理2 假设即期利率rt满足（1）式，股票价格St满足（2）式，则执行价格为K到期日为T的现金或无值看涨期权（CONC）在t∈[0，T]时刻的价值是

其中

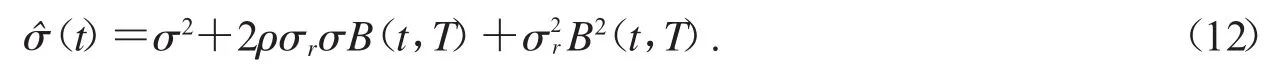
证明：由于这是一个涉及到两个变量的变系数抛物方程的边值问题，直接求解较困难，因此需要通过代换引进新的价格体系.通过引入新的组合自变量和新的未知函数，使得新的未知函数适合的是低一维的定解问题.

对定解问题（9），（10）式引入新的组合自变量（即作自变量代换）以及新的未知函数（即作未知函数代换）

经过初等计算，得

将它们代入（10）式，并在两边同除 P（rt，t，T），得到

将变量代换式（13）以及零息票债券价格 P（rt，t，T）适合方程（5）式代入上式，得到函数在区域{y∈R＋，t∈[0，T]}上适合方程

在边界t＝T上适合的定解条件

令 ξ＝lny，得

则（13）变形为

将上式代入（16），得

将其代入（17），得

其中边界条件是μ（η，0）＝H（*eη－K）

由热传导方程经典解求得方程的解具有如下形式解：

经过变量代换，有

其中

即定理得证.

推论1 假设即期利率rt满足（1）式，股票价格St满足（2）式，则执行价格为K，到期日为T的现金或无值看跌期权（CONP）在t∈[0，T]时刻的价值是

3.2.2 资产或无值期权的定价公式

定理3 假设即期利率rt满足（1）式，股票价格St满足（2）式，则执行价格为K，到期日为T的资产或无值看涨期权（AONC）在t∈[0，T]时刻的价值是

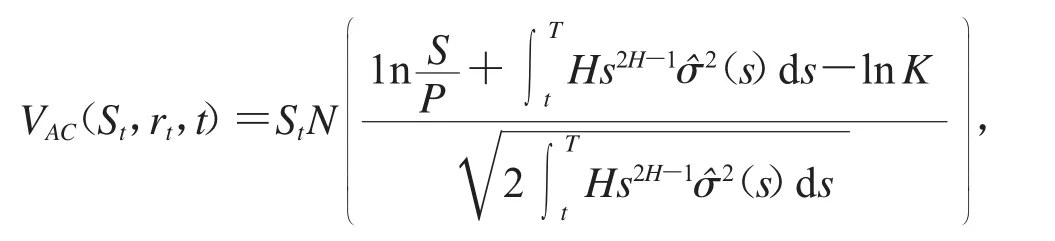
证明：由两值期权所满足的偏微分方程（即引理3）可以得到资产或无值看涨期权定价模型如下

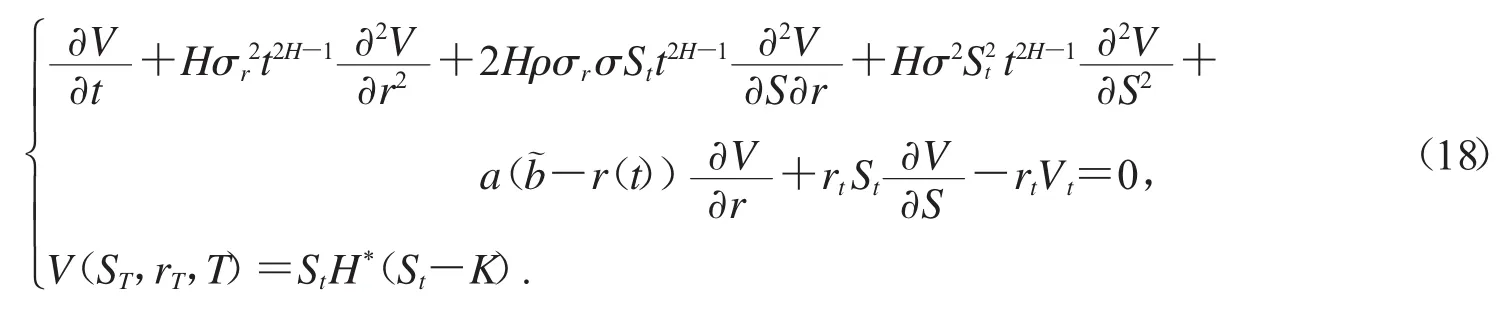
由于资产或无值看涨期权偏微分方程组与现金或无值看涨期权的偏微分方程组的区别在于边界条件不同，故可采用相同的研究思路，变量代换后得

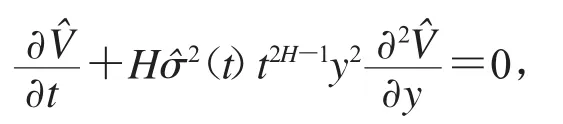
在边界t＝T上适合的定解条件

因而有

其中边界条件是μ（η，0）＝eηH（*eη－K）.

方程的解由热传导方程经典解释论，具有如下形式解：

经过变量代换，得

即定理得证.

推论2 假设即期利率rt满足（1）式，股票价格St满足（2）式，则执行价格为K，到期日为T的资产或无值看跌期权（AONP）在t∈[0，T]时刻的价值是

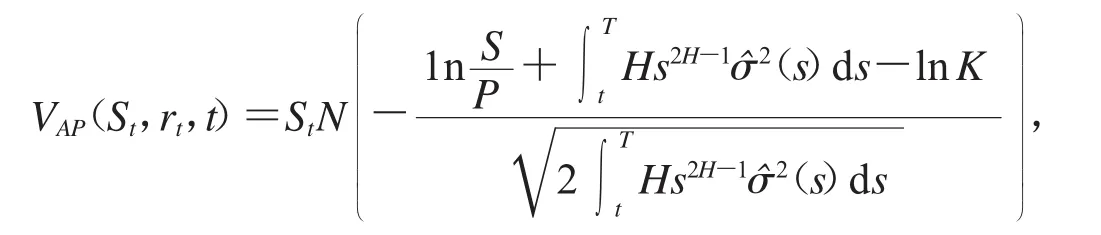
4 结语

本文研究了分数布朗运动和Vasicek随机利率下的两值期权定价问题.由于利率是不断变化的且具有长记忆性，因此考虑随机利率情况下的长记忆型模型更加符合金融市场的实际情况.所得结果丰富了两值期权定价理论，同时为决策者的投资决策提供了相应的参考依据，具有一定的现实意义.对于两值期权定价，还有很多问题值得进一步研究.例如，次分数随机利率、混合分数随机利率下的两值期权等.