次分数布朗运动下带红利的两值期权定价*

叶芳琴，刘文倩，林先伟

（1.汕头大学商学院，广东 汕头 515063；2.汕头大学理学院，广东 汕头 515063）

0 引言

1973年，Black和Scholes提出了著名的B-S定价公式，期权定价理论由此得到了迅速发展[1].然而，在实际的金融市场中，金融资产价格之间具有长期相关性等特点，且金融资产收益率呈现“尖峰肥尾”的特征.1989年，Peter[2]提出用分数布朗运动刻画金融资产价格的变化过程.同时，Bjork和Hult[3]以及Kuznetsov[4]研究发现分数布朗运动描述金融资产的价格变化，会导致此时的金融市场允许有套利机会.国内外的大量学者，采用了修正的分数布朗运动来刻画金融资产价格变化的行为模式，如次分式布朗运动.由于，次分式布朗运动是一种比分数布朗运动更为普遍的高斯过程，它不仅具有自相似性和长记忆性等分数布朗运动具有的性质，而且可将其应用于金融[5].Yan等人[6]给出了次分数布朗运动的随机积分，并指出次分数布朗运动可以用来刻画金融资产的随机波动性.肖炜麟等人[7]研究了在次分式布朗运动环境下带交易费用的备兑权证定价问题，通过引入关于次分数布朗运动的随机积分和偏微分方程技术，得到了在次分数布朗运动下备兑权证的定价模型.李丹等人[8]研究了在次分数布朗运动环境下可转换债券的定价问题，并通过次分数布朗运动的随机积分理论和保险精算的方法，得到了可转换债券的定价公式.

两值期权（binary option）是一种新型的，具有不连续收益的期权.在到期日标的资产价格低于执行价格时该期权一文不值，而当标的资产价格超过执行价格时该期权一文不值，而当标的资产价格超过执行价格时该期权支付一个固定数额.关于两值期权定价的相关研究相对较少.Thavaneswaran等人[9]用模糊集理论的方法对两值期权的定价问题做了一定的研究.袁国军[10]研究了CEV过程下一类两值期权定价的数值解法问题等.

本文在上述研究的基础上，探讨了在次分数布朗运动下带红利的两值期权的定价问题.利用随机分析理论和偏微分方程的方法，建立了次分数布朗运动环境下两值期权的定价模型.通过用偏微分方程的相关知识对此定价模型求解，得到了次分数布朗运动下两值期权定价公式.

1 预备知识

两值期权就是新型期权的一种，两值期权是合同条款变化而产生的新型期权.一般分为两种类型[11]：

（1）现金或无值看涨期权（简写为CONC）：在到期日，若股票价格低于执行价格，则期权价值为零；若大于执行价格，则按规定支付现金1元.

（2）资产或无值看涨期权（简写为AONC）：在到期日，若股票价格低于执行价格，则期权价值为零；若大于执行价格，则按规定支付股价.

引理[7]（次分数Itô公式）假设随机过程St满足以下随机微分方程：

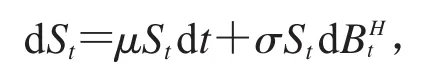
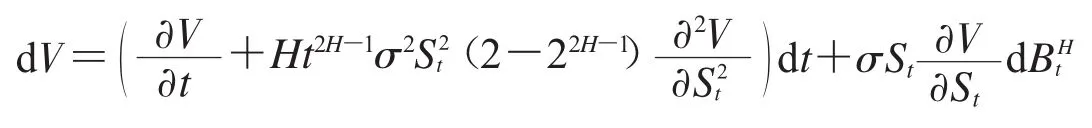
2 基本模型

其中，r是常数，表示无风险利率.

风险资产（如股票）价格St满足下面随机微分方程：

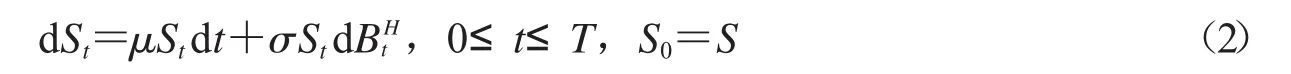
在这里μ，σ是常数，分别表示预期收益率，波动率.

为了得到次分数布朗运动下两值期权定价模型，我们考虑到期日为时间T，敲定价格为K，并作以下假设：

（1）假设资产价格满足（2）式；

（2）无交易费用和税收，允许卖空；

（3）不存在无风险套利机会；

（4）交易是连续进行的.

在风险中性测度条件下，我们利用Δ对冲策略，得到次分数布朗运动下两值期权定价模型.令V＝V（St，t）表示CONC（或AONC）的价格.构造一个投资组合Πt，在时刻t投资组合 Πt的值为：Πt＝Vt－ΔtSt.应用次分数 Itô 公式，在[t，t＋dt]时间段内，

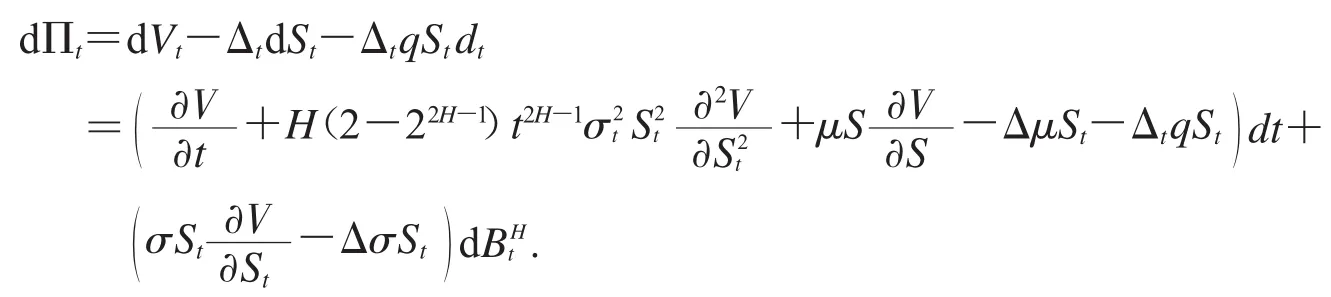
为了使投资组合 Πt在[t，t＋dt]无风险，取，从而可得

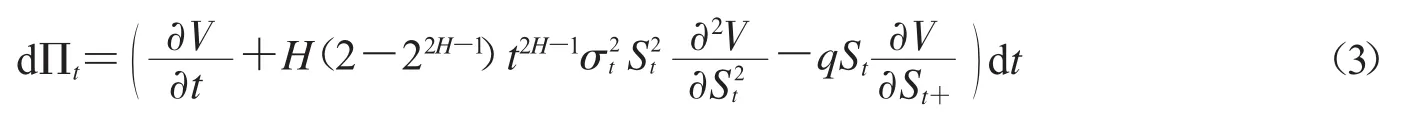
由假设（3），可以得到

将式（3）代入（4），得到

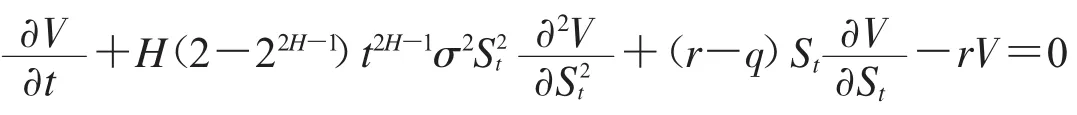
因此，得到在次分数布朗运动下带红利的两值期权定价模型如下：

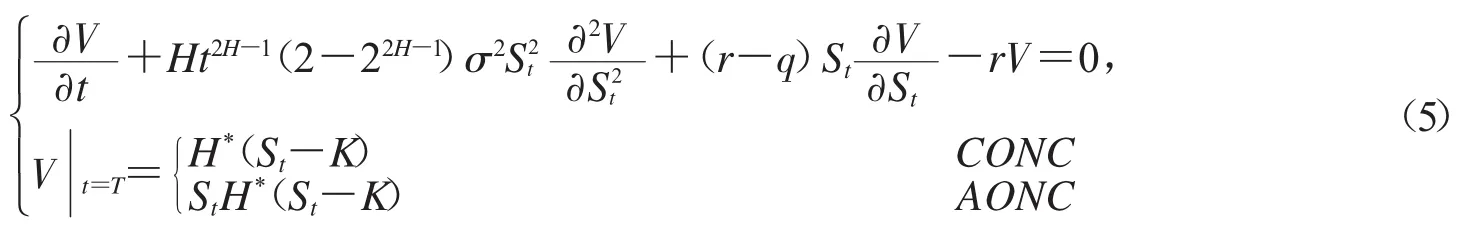
这里，H（*ξ）是Heviside函数.如果ξ＞0，那么H（*ξ）＝1.如果ξ＜0，那么H（*ξ）＝0.

3 两值期权定价公式

3.1 现金或无值期权定价公式

定理1 假设股票价格满足（2）式，在时刻t现金或无值看涨期权的定价公式为：

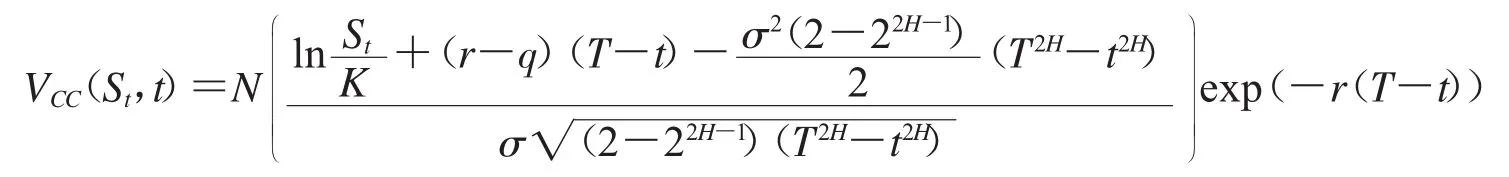
证明：由方程组（5）可以得到现金或无值看涨期权定价模型如下：

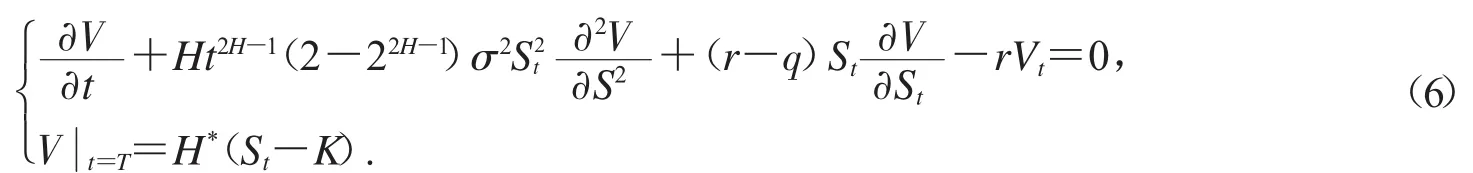
因此方程组（6）转变成如下方程组

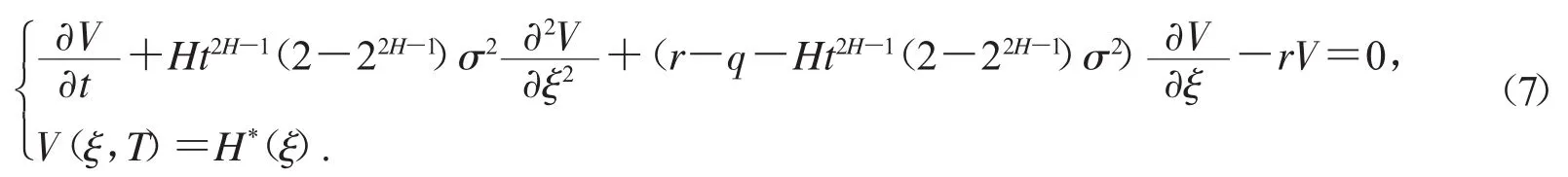
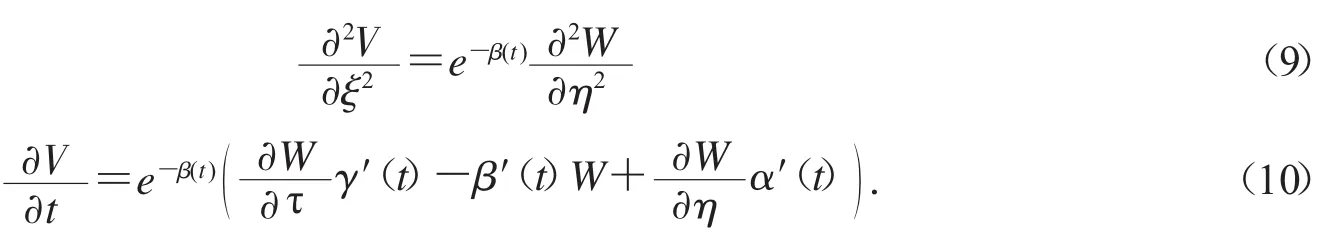
将（8），（9）和（10）代入上述方程，可以得到

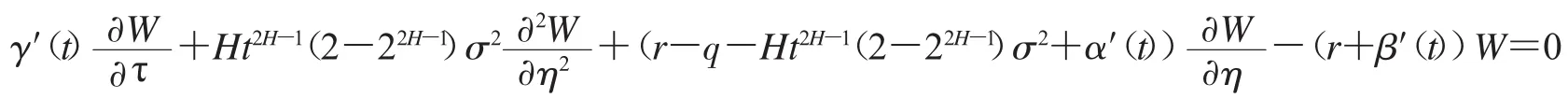
结合终值条件：α（T）＝β（T）＝γ（T）＝0，则得到

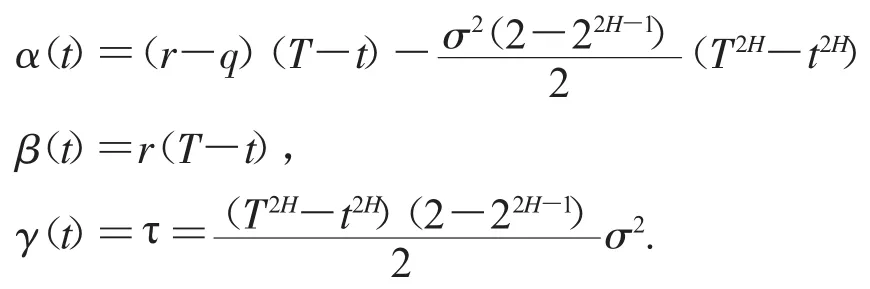
因此，方程组（6）转化为如下行形式：

方程组（11）的解可以用Possion公式如下表示：

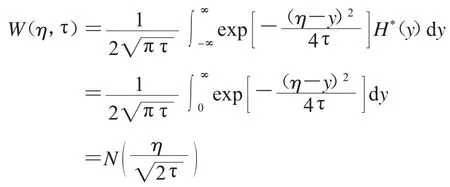
经过变量代换，我们有

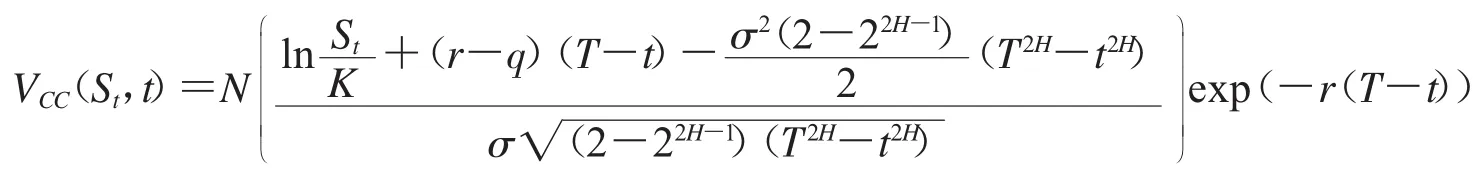
推论1 假设股票价格满足（2）式，在时刻t现金或无值看跌期权的定价公式为：

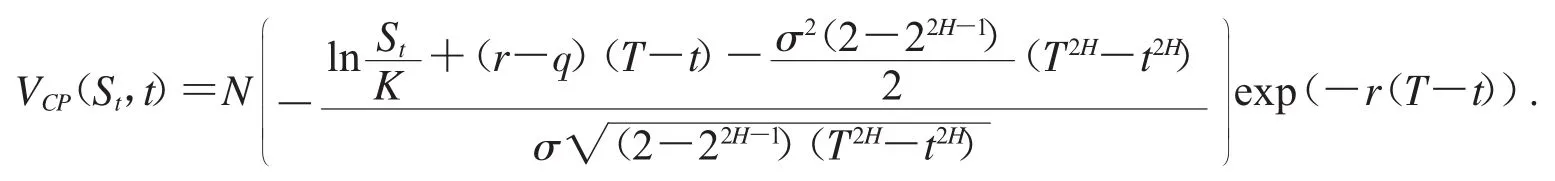
3.2 资产或无值期权定价公式

定理2 假设股票价格满足（2）式，在时刻t现金或无值看涨期权的定价公式为：

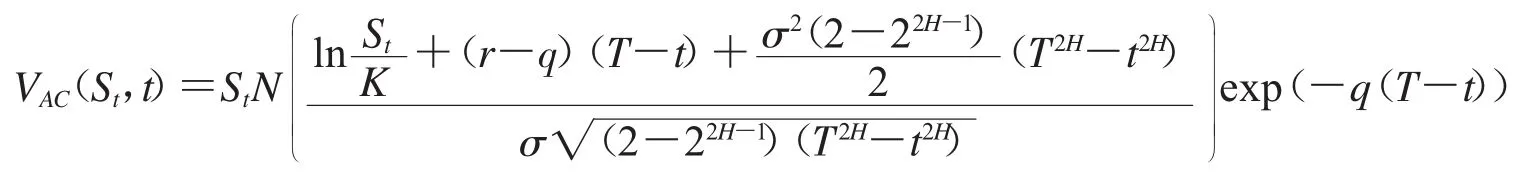
证明：由方程组（6）可以得到资产或无值看涨期权定价模型如下：

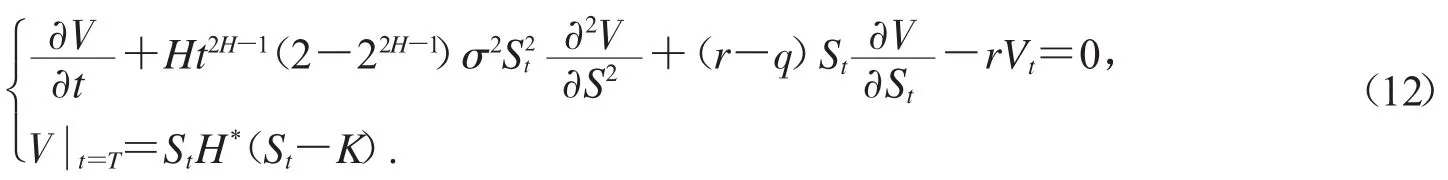
令VA（CSt，t）＝StU（St，t），则，从而可得：

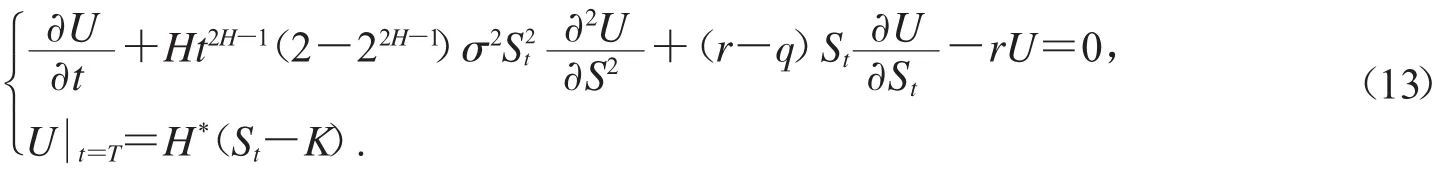
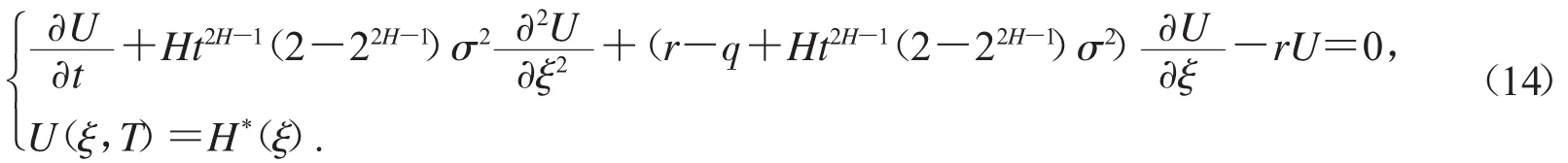
为求解上述 Cauchy 问题，作函数变换 W＝Ueβ(t)，η＝ξ＋α（t），＝γ（t），由于

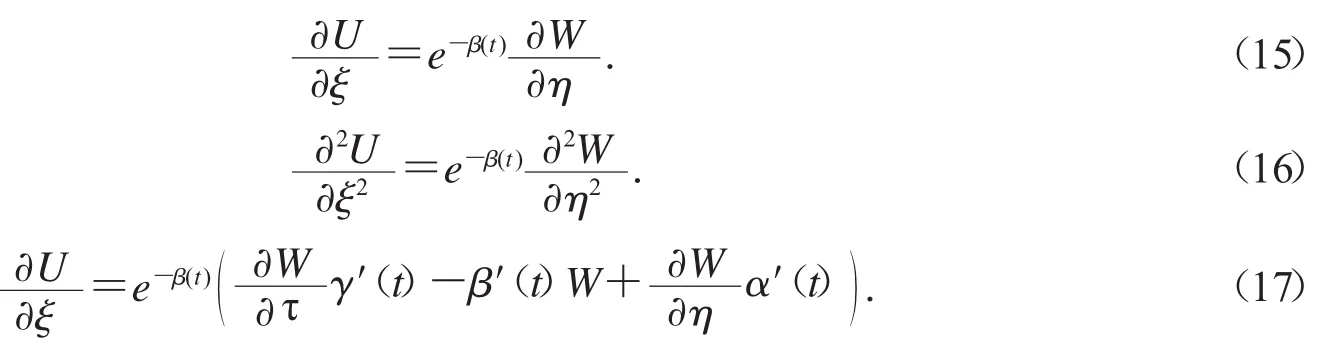
将（15），（16）和（17）代入方程组方程（14），可以得到

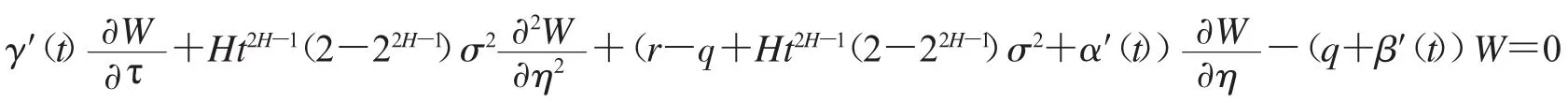
方程组（18）的解可用Possion公式如下：

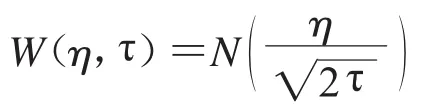
经过变量代换，则有

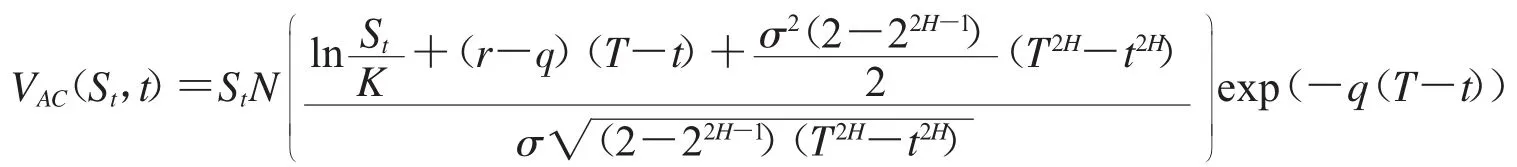
推论2 假设股票价格满足（2）式，在时刻t资产或无值看跌期权的定价公式为：

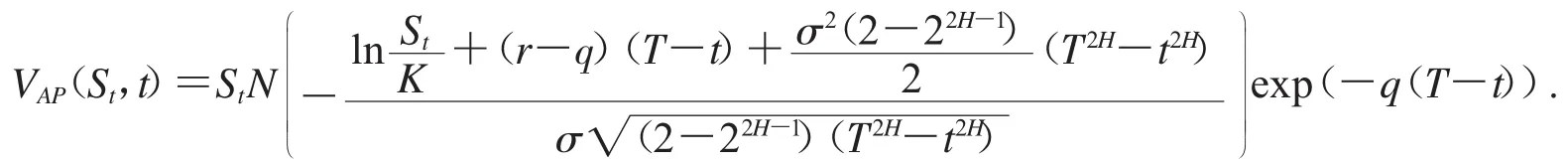
本文在上述研究的基础上，探讨了在次分数布朗运动下带红利的两值期权的定价问题.利用随机分析理论和偏微分方程的方法，建立了次分数布朗运动环境下两值期权的定价模型.利用偏微分方程的相关知识求解此模型，推导出了CONC和AONC定价公式，并在此基础上得到了有关AONP和CONP定价公式的两条推论.对于两值期权定价，还有很多问题值得研究.例如，在带跳的分数布朗运动或带跳的混合分数布朗运动环境下研究此类问题.