振动修整过程中三维介质运动离散模型的研究∗∗

姬清华

(新乡学院，河南 新乡453003)

近年来，振动修整工艺以其较高的表面质量创成性广泛应用于精密加工领域。振动修整加工能够获得所需表面粗糙度的同时，也创造了各向同性的表面织构，有利于缩短加工时间和加工成本[1-3]。

然而，由于机械加工系统的复杂性，振动修整工艺优化设置通常是基于经验实验和误差方法确定的。虽然目前有较多的研究学者对于“最佳”振动修整工艺进行了研究，但是大部分工作是基于实验完成的，缺少相应的理论基础。特别地，对于振动修整过程中进行优化的介质运动建模方法还没有得到广泛的应用，且对机械容器内介质运动的理解还不够深入[4]。随着科技发展对于加工性能要求的不断提高，能够准确预测最佳工艺参数、修整工件表面粗糙度和最佳去除率的振动修整模型显的尤为重要。因此，有必要研究一种振动修整系统的介质动态运动模型，以便对其进行控制、预测和优化。

现有研究中，虽然Hashimoto等人[5]建立了一个用于预测表面粗糙度和表面去除率的初始振动修整机床模型，但该模型没有考虑到机器内部的介质相互作用；随后他们又对其模型进行了改进，但没有包括与周围颗粒的单独颗粒相互作用[6-7]。为了更准确地预测接触颗粒之间的接触力和移动速度，需要利用离散单元对特定振动模式下的振动修整工艺进行建模，这是由于离散元法(DEM)适合大量离散单元同时接触的情况[8-9]。

基于以上研究，利用离散元法(DEM)和ABAQUS仿真软件的EXPLAL模块建立振动修整三维离散模型，研究振动修整过程中介质运动动态机理；利用DEM定义抛光颗粒之间以及颗粒与容器之间的接触情况，从而确定颗粒之间的接触力和碰撞速度；结果表明，颗粒之间的冲击力和速度与接触参数的设置和基本接触参数的变化有很大关系。

1 振动修整模型

振动修整工艺原理如图1所示，装有介质和工件的容器通过弹簧系统与底座联接。容器振动运动由机床系统中偏心放置的不平衡旋转轴产生，容器中颗粒存在两种不同的运动:容器振动引起的大尺度介质流动和颗粒撞击周围粒子的小尺度振动运动。图中箭头显示了介质和工件流的横向运动和垂直运动。基于ABAQUS/EXPLISH模块建立球形介质颗粒填充的三维球式振动修整模型，容器的运动受4个等间距水平弹簧和4个水平阻尼器，4个等间距垂直弹簧和4个垂直阻尼器的约束。上下重量分别表示为mt和mb，通过可调的相位角φ与旋转轴相连。旋转轴转速设置为ω＝144.9 rad/s。所建立的模型的基本设置和参数如表1所示。

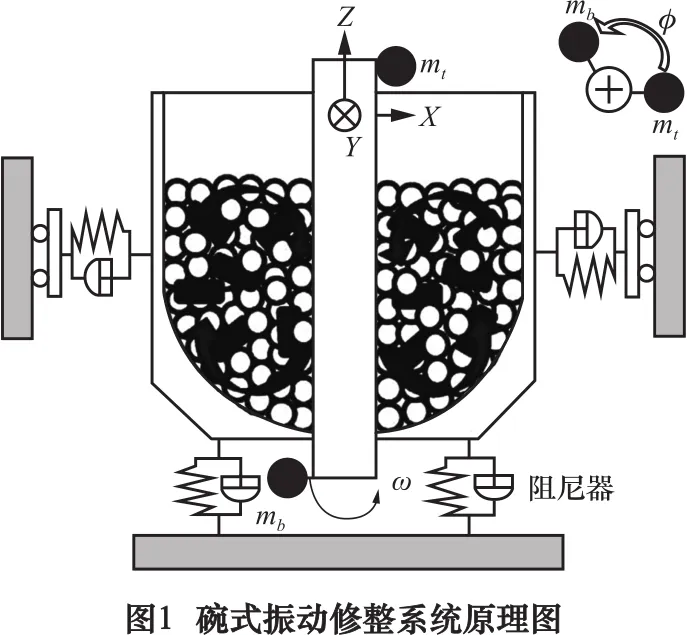
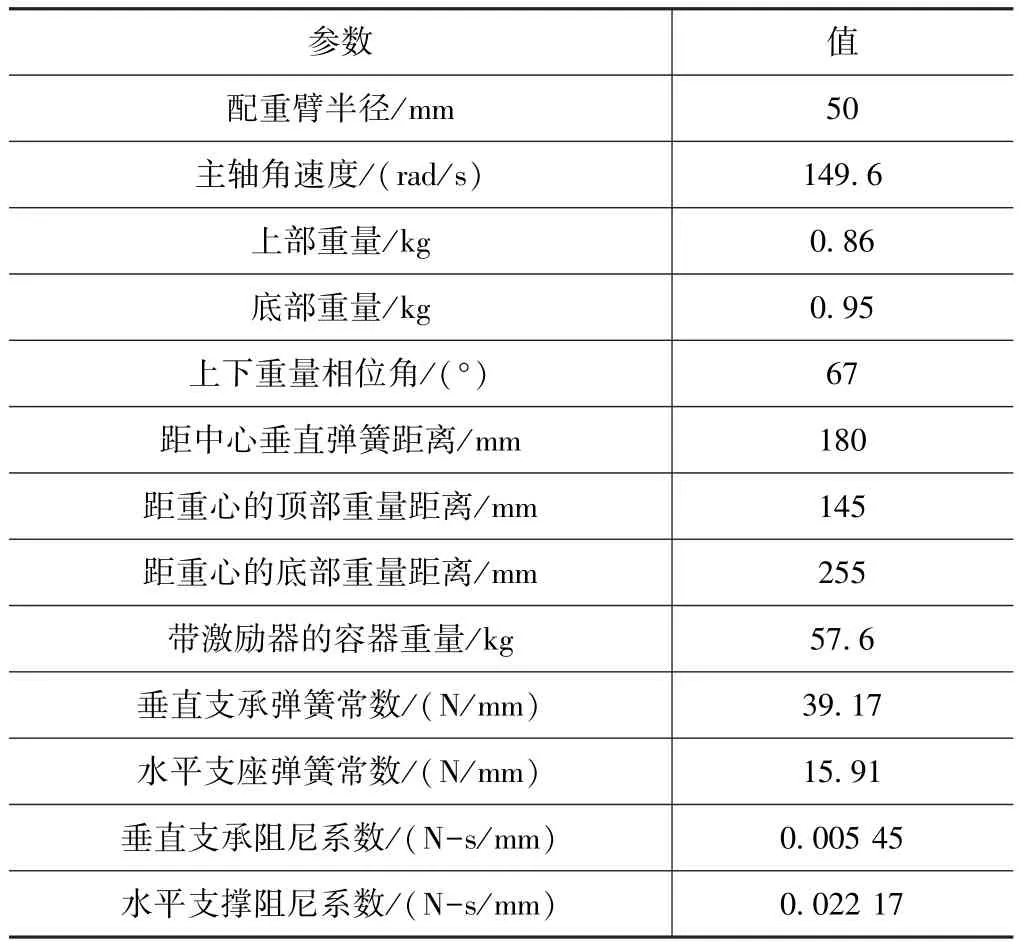
表1 模型基本设置和参数

振动修整过程中工件材料去除率和塑性变形取决于振动激励模式，并受相位角、振动频率、介质接触刚度以及由此产生的介质速度等的影响。利用离散元法(DEM)确定粒子之间以及容器边界表面与粒子之间的相互作用力，假定容器壁面为刚体表面，表面摩擦系数设置为0.35。仿真模型包括两个步骤:一是在容器中填充考虑引力的粒子；二是设置不平衡旋转轴转速为ω＝144.9 rad/s，以诱导容器振动产生振动修整所需要的介质激励。采用表1所述的初始安装和操作参数进行振动修整机模型进行模拟。通过对粒子轨迹的分析，对用于模拟的非线性接触关系进行优化。该模型产生了单个颗粒的三维运动和振动容器内介质的体积流动。由于离散元素粒子代表单个粒子，因此对每个粒子使用一个刚性单元，将每个粒子描述为具有指定半径的刚性球形的单节点元素。此外，在Z方向上以9 800 mm/s2的加速度向系统施加重力感应载荷。

2 离散单元法

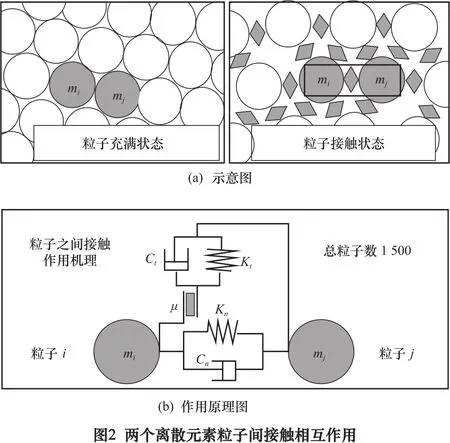
基于Hertzian接触理论计算相互作用粒子之间和颗粒与容器壁之间的法向接触力Fn和切向接触力Ft，考虑非线性弹性理论模型中接触刚度、重叠度、阻尼系数和摩擦力。图2为两个离散元素粒子之间的接触相互作用，采用表格形式的压力-超封闭关系来定义介质的接触刚度。在ABAQUS/Explicit模块中，容器中撞击粒子的能量通过粒子之间以及粒子与容器之间的接触摩擦和阻尼逐渐消散。切向力受库仑摩擦力的约束，可以表示为:

式中:μ表示颗粒之间和/或颗粒与容器壁之间的摩擦系数。作用于粒子表面的切向接触力会引起粒子中心力矩，DEM粒子的相互作用是通过接触界面进行力矩传递。

3 仿真和实验结果

建立了一种三维碗式振动精整机模型，对容器内的球形介质流动进行显式动态模拟。仿真过程中，粒子彼此碰撞并与容器壁表面碰撞，基于ABAQUS/Explicit模块建立修整机模型和介质运动方程系统。其中，重力加速度作用于振动精整机模型坐标系的Z方向，系统的横向运动为X和Y方向。

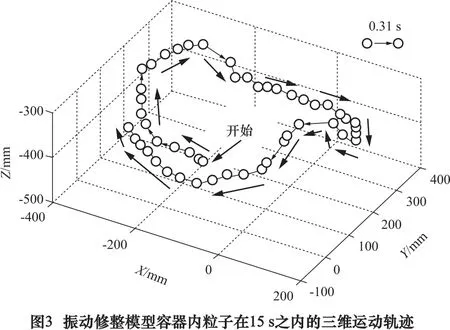
图3为振动修整模型容器内粒子在15 s之内的三维运动轨迹，每个圆圈显示的是粒子的位置。圆圈由箭头连接，箭头表示粒子的运动方向。粒子围绕容器内的旋转轴完成一次完整的旋转，确认容器的振动运动在X、Y和Z方向上都会产生粒子运动。粒子的行进方向由其周围粒子施加在粒子上的合力决定。从开始点起，粒子向外侧壁面移动的同时向上移动；然后，粒子向内侧壁面移动的同时向下移动。粒子重复这种向上和向下的垂直运动，以及向内和向外的横向运动，为一个螺旋-环形运动。相位角设置为φ＝67°时，容器内的所有粒子都以这种典型的螺旋-环形运动，其振荡幅度和频率相似，而与它们的位置无关。

图4为所选粒子在容器内X、Y和Z方向上相对于时间的位置。容器外壁半径为266.5 mm，内侧壁面半径为120 mm，深度为185 mm。由图4a和图4b可知，粒子在容器内水平运动，其横向运动可以描述为一个周期为13.7 s的正弦函数；图4c显示了容器内该颗粒相对于时间的垂直位置，颗粒垂直位移的周期为4.34 s。该粒子的平均垂直位移为100 mm。颗粒表现出重复的垂直循环运动，即颗粒首先从容器底部循环到顶部自由表面，然后从顶部自由表面循环到容器底部。粒子在X、Y和Z方向上的三维位置说明了粒子在容器内沿着螺旋线运动。

这种介质运动可以通过两种撞击接触机理来描述:首先，接触力从振动容器壁面撞击到任何粒子的过程中，使粒子产生振动运动；第二，由于粒子之间的撞击接触，相互作用的粒子出现滚动和滑动现象，这些撞击力在粒子之间传递振动运动。这两种撞击机理的组合是碗式振动修整中球形粒子运动的驱动力。

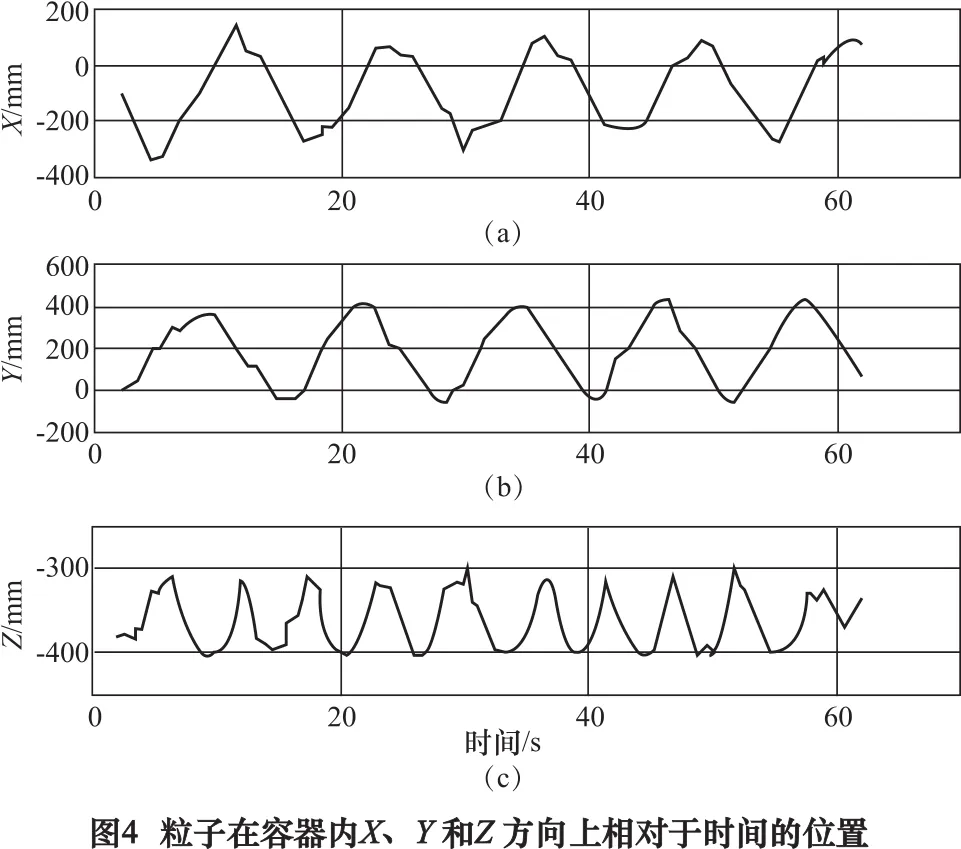
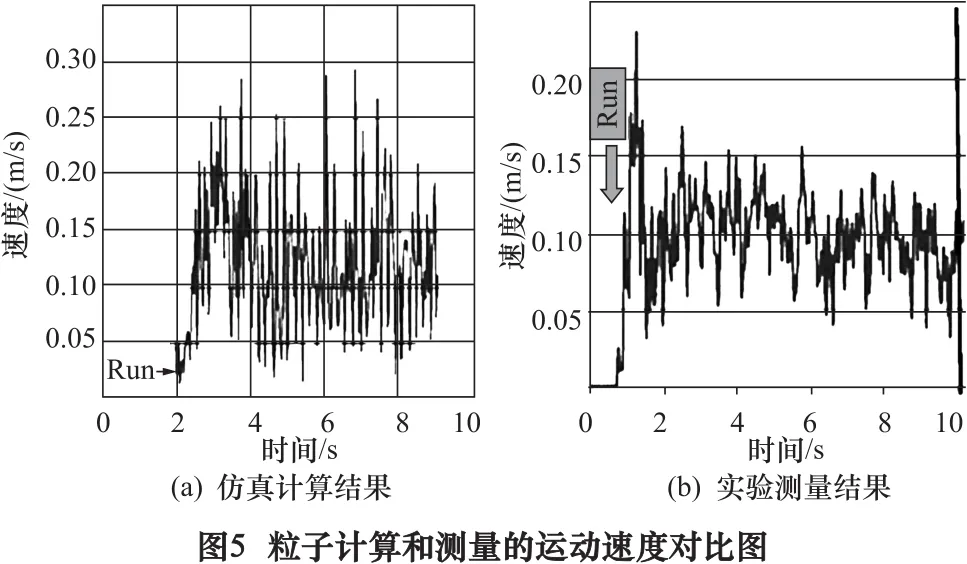
图5为粒子计算和测量的运动速度对比图。在0.02～0.3 m/s，粒子的瞬时速度与计算结果和实测结果都有很大的差异。图6表示在同一时期内作用于自由落体介质中相应粒子的法向接触力的大小，其法向接触力在0～3.7 N随机变化。

另外，该模型已经用特定的颗粒接触刚度、阻尼系数和接触物体之间的摩擦系数进行了校准。图7是相位角φ对介质平均速度的影响。由图可知，计算得到的粒子速度在相位角为φ＝90°时达到了最大值0.12 m/s，而相位角为 φ＝67°时粒子速度为0.11 m/s，而在相位角为φ＝0°和φ＝180°时期粒子速度相对较小。同时，相位角由67°增加到90°时粒子速度逐渐增加。

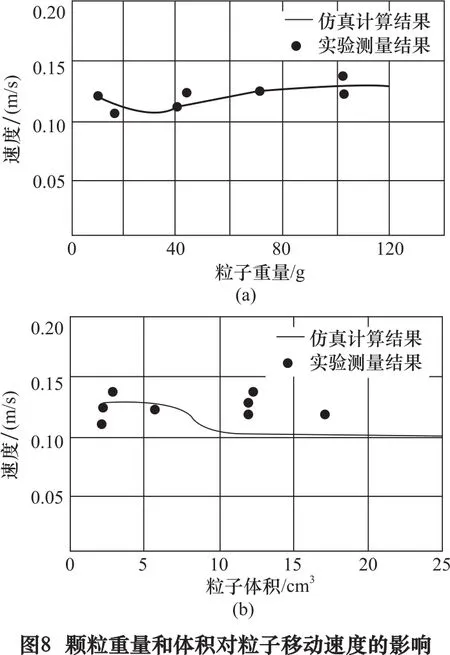
图8a为颗粒重量对粒子移动速度的影响。计算和测量结果表明，在相角为φ＝67°时，平均介质传播速度保持恒定，速度为0.11 m/s的粒子重量对应于6.1～122.0 g。这表明粒子重量对粒子运动速度的影响是可以忽略不计的，同时证实了不同重量的工件的运动速度与周围介质的流动速度大致相同。图8b为粒子体积对粒子运动速度的影响。体积范围为1.3～22.5 cm3。对于体积范围，计算和测量的介质速度值受体积影响不显著。因此，较大尺寸的工件不会覆盖周围的介质流模式，在振动精整机中可以一定程度上容纳各种工件尺寸。

4 结语

本文基于ABAQUS仿真软件中的Explicit模块，建立三维振动修整系统内部介质离散运动模型，对系统介质运动(粒子间、粒子与修整容器壁面间的碰撞运动及速度和位移情况)进行了数值模拟。仿真获得的介质运动对颗粒间的接触刚度、颗粒与容器壁之间的接触刚度以及颗粒间的阻尼系数都有较好的敏感性。实验结果表明，本文提出的基于离散单元法的动态振动精整系统模型能准确预测介质流动和局部撞击颗粒的介质运动。此外，该模型还可以通过参数设置调整颗粒运动模式和速度，以最大限度地提高材料的去除率。