基于建构主义的初中数学后进生习题错误成因及对策
2019-02-26何苑子
何苑子


摘要:学生获得知识的主要途径是课堂教学,这也是“后进生”转化的主要途径。通过观察后进生错误习题总结出数学学困生的形成原因,并利用建构主义理论进行分析研究,这符合当前新课程改革的要求,且与传统教学中“满堂灌”“一刀切”等教学模式形成了鲜明的对比,更易于吸引学生的注意力。教师要重视后进生的习题错误,对后进生的习题错误进行收集整理,在教学中针对不同的后进生、不同的错误,对症下药,将错误彻底消灭。
关键词:初中数学;后进生;建构主义;错题;成因;对策
一、建构主义的主要观点
兴趣是最好的老师。对于后进生的学习,建构主义注重让后进生主动参与学习,其体来说,在知识观方面,其注重后进生对知识的生成以意义建构的方式获得,而非简单且被动地接收信息;在学习观方面,建构主义更重视师生之间的协作交流,学生在主动探索活动中获得知识并完成学习任务;在教学观方面,建构主义注重让教学按照后进生的思路及接受方式进行,在了解后进生原有经验知识的前提下,找出新旧知识的契合点,对于知识的理解,重视以后进生自己的认知方式去进行,最终达到让学生独立学习的目的。
二、教学中后进生常犯习题错误
1.概念不清楚、判断不恰当,归根结底是没有认识掌握必要的知识。尤其表现在对数学概念的理解以及运算技能上,这些影响初中数学的学习
对策:正确看待后进生的习题错误,强调后进生在学习过程中以他们原来的知识经验背景为基础主动建构新知识。错题和知识点是现象和本质的关系。更正错题是后进生在学习中重要的一个环节,后进生通过更正错题可以不断完善知识和加深对概念的理解,提高其解题的能力。
例如:(-2)2和-22,很多后进生都以为其结果是4,而正确答案是第一个数的结果4,第二个数的结果是-4。错误原因是学生以为(-2)2和-22都表示2個-2相乘,但是在第二个数中,负号和2是没有用括号括起来的,因此表示的是2的平方的相反数,不是一2的平方。再如9的算术平方根,其结果是3才对,可学生往往写成±3,其错因是对平方根和算术平方根的概念理解不透彻。
2.知识点混淆,受题目中隐藏条件或表面干扰,出现想当然的解题错误
对策:对学生的错误教师要以宽容的态度对待,重视错题中合理成分的提取和激活,使后进生认识到自己对和错的地方,并对自己的想法和做法进行修改和调整。
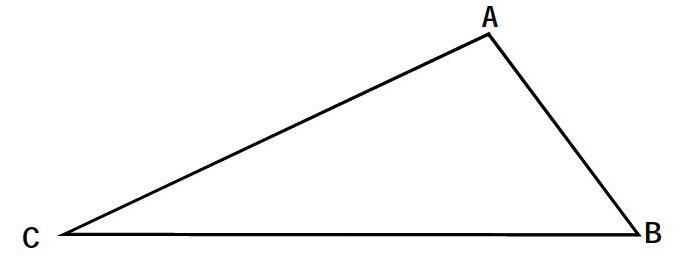
例如:已知如图,△ABD和△AEC都是等边三角形,求证BE=DC。
错解:∵△ABD和QAEC都是等边三角形
∴∠BAD=60°=∠CAE
∠CAD=∠EAB=120°
又∵AB=AD AE=AC
∴△ABE≌△ADC
∴BE=CD
错误原因分析:只靠眼睛主观臆断,认为D、A、E三点在同一直线上,想当然地得到∠CAB=60°是造成错误的主要原因。其实D、A、E三点不一定在同一直线上,∠CAB的大小是不确定的,事实上D、A、E三点不一定在同一直线上,所以这道题是要证明∠DAC=∠BAE。在解答几何证明题时后进生常犯这种错误,所以在教学中要提醒学生读题时弄清楚题目中的已知条件和隐含条件,不能胡乱添加条件,对于隐藏的条件要合理使用。错误是后进生学习的最佳时机,教师不仅要引导后进生发现错误,而且要比较不同的解法。要使学生明白犯这种错误的原因同时又能指出这种蜀昊在解题中的合理成分,使后进生实实在在得到帮助和提高。
3.缺乏分析问题和解决问题的能力,逻辑推理能力较差
对策:引导他们根据题意分析题中的已知量和未知量,遇到这些问题应该用什么知识点来解决,不给他们现成答案。在解题中要及时发现他们在解答中出现的错误并纠正。
建构主义理论认为同化和顺应是学习者认知结构发生变化的两种途径或方式。学习过程不是纯粹的信息输入、存储和提取,是新旧知识相互作用的过程。在解题中让后进生主动参与找出错误,说出错在什么地方,哪个知识点用错,对后进生来说是一种宝贵的经验。建构主义理论强调知识并不是对现实的准确表征,它只是一种解释、一种假设,它并不是问题的最终答案。在课堂上教师可主动展现错误过程,通过模拟错误还原后进生可能出现的各种解题错误,找出错误的原因,及时解决后进生的解题困惑。
4.方法欠妥,思维僵化,思路不够开阔
对策:提高学生的解题技巧,对同类型的题形成解题规律,以便达到触类旁通;尽量挖掘试题的深度和广度,培养学生应变能力,降低盲目解题出现的错误。
例如:如图,在△ABC中,AC=8,BC=10,且AC>AB。
(1)用尺规作图法在△ABC内求作一点D,使点D到A、C两点的距离相等,又到边AC、BC的距离相等(保留作图痕迹,不写作法);
(2)若△ACD的周长为18,求△BCD的面积。
对于这种作图题目单纯满足一个结论他们会做,但两个结论同时满足他们就无所适从,不知从哪下手;(2)问中学生更不会从(1)问中寻找有用的结论来解决,说明后进生思维定式,思路不开阔,不会延伸和扩展。在平时教学中要注重培养后进生的解题技巧和应变能力,让学生主动去探究和发现。
我们都知道教材中的例题和习题都是编者们精挑细选的,具有很强的示范性和典型性,也给教师和学生留下了很大的思考和创新空间,只要我们肯花时间努力钻研,把这些例题、习题进行加工、打磨,可以促使学生拓展延伸,类比迁移。
例如:在△ABC中,CD是AB边上的高,且CD2=AD·BD,求∠C的大小。
题目中所给出的图形是平面几何中比较常见而且比较经典的图形。由已知条件可得Rt△ACD~Rt△CBD,
从而得到∠A=∠BCD,∠B=∠ACD,故∠ACB=90°。
变式:如图,AB是⊙O直径,CD是⊙O的弦,
CD⊥AB,CD与AB相交于点P,求证:PC2=PA·PB。
这种变式是上面例题的升级版,加了圆的知识点在里面,由AB是⊙O直径得到∠ACB是直角,再由CD⊥AB得到Rt△ACP~Rt△CBP,从而证到PC2=PA·PB。通过这种训练可以加强后进生思维的变换和扩展,举一反三,力求讲一例通一类,为学生打好基础,让后进生在学习中逐渐领会要领、找到乐趣;也使学生能够完全熟练掌握和应用所学知识点。必要时可以让学生自己去编题和做题,这样既可发现自己的不足,又可以探究新的知识。再次要求学生建立错题集,后进生每周都会积累一些错题,所以同学之间每周要开展纠错交流,交流一下解题经验与技巧。要学生知道哪里错,引导学生反思错误的原因,以提高学生自我诊断能力,强化思维能力。建构主义学习理论所提倡的学生合作学习,有助于改善竞争环境下的学风,说明知识不仅是通过教师传授获得的,学习者在一定的情况下,可以借助于其他人(包括教师和学习伙伴)的帮助,利用必要的學习资源,通过意义建构的方式获得。
建构主义认为学生不是被动接受者和被灌输的对象,而是信息加工的主体,是意义的主动建构者。学生要成为意义的主动建构者,就要求后进生在学习过程中要用探究法去建构知识。要后进生主动搜集并分析有关的信息和资料,对所学习的问题提出各种假设并加以验证,从中获得经验和知识。
综上所述,在当代初中数学教学中,能让后进生在错误习题中找出错误之处并说出错的原因尤为重要,对后进生来说已经成功了。没有改不了的错误,只有不愿改的态度。文章运用了建构主义思想方法,探讨了建构主义在其中的有效运用,以期能为当前初中数学教学提供有益参考,促进后进生更高效学习。通过改进教学,我们可以有效地帮助后进生减少错误的发生。
参考文献:
[1]孙桂芹.建构主义理论对高校普通心理学教学模式改革的启示[J].兵团教育学院学报,2012,22(5):40-43.
[2][瑞士]皮亚杰(J·Piaget),海尔德(B·Inheader).儿童心理学[M].商务印书馆,1980.
[3][瑞士]皮亚杰.结构主义[M].商务印书馆,1984.
编辑 张佳琪
