统计学习直通车

■王佩其

一、学习要点梳理

1.随机抽样

随机抽样包括简单随机抽样、系统抽样和分层抽样，三种方法虽然有所不同，但无论哪种抽样，每个个体被抽取的可能性都相等。

2.数据处理的常用图表

（1）茎叶图：当我们收集的样本数据不是很多，且又不是太分散时，可以用茎叶图进行处理，茎叶图可以保留所有数据，而且可以随时记录数据。

（2）频率分布表：当数据较多且是一些特殊数据时，可以考虑列出频率分布表，频率分布表可以较清晰地看出数据之间的联系。

（3）频率分布直方图：有时数据较为复杂，要想从数据中获得较为准确的结果，仅靠一方面的分析还可能不理想，此时可以通过频率分布表来绘制频率分布直方图，借助图形产生结论。

（4）散点图：对于附加条件的数据，可借助散点图，利用基本函数的图像来处理。

3.四种样本数字特征的应用

样本的数字特征主要是指样本数据的平均数、众数、中位数、标准差（方差）。

众数体现了样本数据的最大集中点，容易计算，但它只能表达样本数据中很少一部分信息，显然对其他数据信息的忽略使其无法客观地反映总体特征。

中位数是样本数据所占频率的等分线，它不受少数几个极端值的影响，容易计算，它仅利用了数据中排在中间数据的信息，但它对极端值的不敏感有时也会成为缺点。

平均数与每一个样本的数据有关，“越离群”的数据，对平均数的影响也越大，所以任何一个样本数据的改变都会引起平均数的改变，这是众数、中位数都不具有的性质。也正因为这个原因，与众数、中位数比较起来，平均数可以反映出更多的关于样本数据全体的信息，但平均数受数据中的极端值的影响较大，使平均数在估计总体时可靠性降低。

4.求线性回归方程的方法

（1）回归分析是对具有相关关系的两个变量进行统计分析的方法。两个变量具有相关关系是回归分析的前提。

（2）散点图是定义在具有相关关系的两个变量基础上的，对于性质不明确的两组数据，可先作散点图，在图上看它们有无关系，关系的密切程度，然后再进行相关的回归分析。

（3）求回归直线方程，只有在散点图大致呈线性时，求出的回归直线方程才有实际意义，否则求出的回归直线方程毫无意义。求回归直线方程通常用待定系数法。

二、基本题型分析

例1我国古代数学专著《九章算术》中有一衰分问题：今有北乡八千一百人，西乡七千四百八十八人，南乡六千九百一十二人，凡三乡，发役三百人，则北乡遣（ ）。

解：由题意可知，这是一个分层抽样问题，其中北乡可抽取的人数为300×应选B。

评注：本题属于分层抽样问题，是高考中出现频率最高的抽样问题。分层抽样适用于总体中个体差异较大的情况，其解题思路如下：①求某层应抽个体数量，即按该层所占总体的比例计算。②已知某层个体数量，求总体容量，即根据分层抽样就是按比例抽样，列比例式进行计算。

例2为了解某校教师使用多媒体进行教学的情况，采用简单随机抽样的方法，从该校400名授课教师中抽取20名，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如图1所示。据此可估计该校上学期400名教师中，使用多媒体进行教学次数在［16，30）内的人数为 。

图1

解：观察茎叶图，可知抽取的20名教师中使用多媒体教学次数在［16，30）内的有8人，所以该区间段的频率为，因此全校400名教师使用多媒体进行教学次数在［16，30）内的人数为400×0.4=160。

评注：茎叶图便于数据的记录和表示。由茎叶图可以清晰地看到数据的分布情况，但当样本容量较大时，作图较烦琐。

例3一次科技知识竞赛，两组学生的成绩如表1所示（满分为100分）。

表1

已经计算得知两组成绩的平均数都是80分，请根据你所学过的统计知识，进一步判断这两个组在这次竞赛中的成绩谁优谁差，说明理由。

解：甲组成绩的众数为90分，乙组成绩的众数为70分，从成绩的众数比较看，甲组的成绩好一些。

由表中数据可知，两组均有学生50人，两组的平均数都是80分。利用方差公式容易得到s2甲=172，s2乙=256。因为s2甲＜s2乙，所以甲组的成绩比乙组的成绩稳定。

甲、乙两组成绩的中位数、平均数都是80分，其中甲组成绩不低于80分的有33人，乙组成绩不低于80分的有26人，从这一角度来看甲组的成绩较好。

从成绩统计表来看，甲组的成绩不低于90分的有20人，乙组的成绩不低于90分的有24人，所以乙组成绩集中在高分段的人数多，同时乙组得满分的人数比甲组得满分的人数多6。从这些角度来看，乙组的成绩较好。

评注：在实际问题中，仅靠平均数不能完全反映问题，还要研究方差，方差描述了数据相对平均数的离散程度。在平均数相同的情况下，方差越大，离散程度越大，数据波动性越大，稳定性越差；方差越小，数据越集中，稳定性越好。

例4某电子商务公司对10000名网络购物者2018年度的消费情况进行统计，发现消费金额（单位：万元）都在区间［0.3，0.9］内，其频率分布直方图如图2所示。

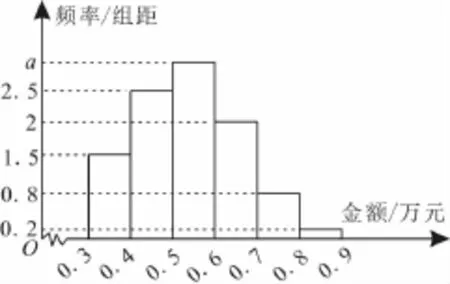
图2

（1）直方图中的a=____。

（2）在这些购物者中，消费金额在区间［0.5，0.9］内的购物者的人数为____。

解：（1）由频率分布直方图及频率之和等于1，可得0.2×0.1+0.8×0.1+1.5×0.1+2×0.1+2.5×0.1+a×0.1=1，解得a=3。

（2）消费金额在区间［0.5，0.9］内的频率为0.2×0.1+0.8×0.1+2×0.1+3×0.1=0.6，所以消费金额在区间［0.5，0.9］内的购物者的人数为0.6×10000=6000。

评注：频率分布直方图是高考考查的热点。用样本的频率分布来估计总体分布的重点是频率分布表和频率分布直方图的绘制以及用样本的频率分布估计总体分布，难点是频率分布表和频率分布直方图的理解及应用。在计数和计算时一定要准确，在绘制小矩形时宽窄要一致。通过频率分布表和频率分布直方图可以对总体作出估计。