基于DFA的股市极端波动率阈值的确定及应用——基于系统动力学视角

苑 莹 于昕彤 张同辉

(东北大学 工商管理学院， 辽宁 沈阳 110169)

1 研究方法

当金融市场的演化状态处于极端波动时，去除这些极端状态对系统的长程相关性几乎没有任何影响；当市场的演化状态为非极端值时，去除不同非极端状态后的DFA指数彼此之间有很大差异。基于这一思想，本文以消除趋势波动分析方法为基础和主要方法，确定股市波动率的极端阈值，从而对上证指数极端波动率进行研究。

1.1 消除趋势波动分析(DFA)方法

DFA方法提供了一种测量非平稳时间序列长记忆性相关强度指数的方法。与其他方法相比，它的优势在于可以测量非平稳时间序列长程相关性的相关强度，也能避免非平稳时间序列存在的虚假长记忆性。

对给定长度为N的序列{xi}，i=1,2,…,N，DFA方法的一般过程如下：

(1)通过求和把原序列归并成一个新的序列：

(1)

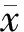
(2)把序列yi分割成长度为s的Ns=int(N/s)个互不相交的等长区间，由于长度N经常不是s的整数倍，为了不丢弃尾部剩余部分，从序列尾部重复这一分割过程，因此得2Ns区间。

(3)通过最小二乘法拟合每一子区间v(v=1,2,…,2Ns)上的局部趋势pv(j)函数消除子区间v中的局部趋势序列：

Zv(j)=yv(j)-pv(j) (j=1,2,…,s)

(2)

(4)分别计算2Ns个消除趋势子区间序列的平方均值：

(3)

这里v=1,2,…,Ns，进而求出这2Ns个F(s,v)的均值平方根：

(4)

(5)在双对数图中分析波动函数F(s)与s的如下关系：

F(s)∞Sa

(5)

对每一个分割长度s，可求出相应的一个波动函数值F(s)，作出Ln(F(s))～Lns函数关系图，其斜率为标度指数α。

α体现了序列的相关特性：当α=0.5时，意味着该序列不存在长记忆性。若时间序列仅是短期相关，α值会十分接近于0.5；当0.5<α≤1时，说明时间序列具有状态持久性，即该序列存在长期记忆特征，当前的事件和未来事件之间存在长程相关性；当0<α<0.5时，时间序列具有状态反持久性，即如果一个时序在前一个期间存在一个向上(下)趋势，则它在后一个期间很可能存在向下(上)的趋势。通过分析极值对系统h(q)(DFA的值)的影响来确定极端事件的阈值。

1.2 确定极端事件阈值的方法

由DFA方法得到的DFA指数值能确定在一定的时间内系统演化的长程相关性，而极端事件不会(或很小)影响整个系统的长程相关性。因此，DFA值能确定极端事件的阈值。假设xi是长度为n的序列xi(xi，i=1，2，3，…，n)，确定极端事件的阈值包括以下几个步骤：

(1)找出xi的最大值xmax和最小值xmin；

(2)计算出xi的中点(R)，可以是xi的平均值或中值；

(3)从xmax开始，依次舍去xi区间{xi，xi≥xmax-d×k}内的值，直到xi=R，可以依次得到新的序列yj(j=xmax-d×k)，其中d是区间间隔，k=1，2，3，…，(R-xmax)/d。同样地，从xmin开始，依次舍去xi区间{xi，xi≤xmin+d×k}内的值，直到xi=R，则依次得到新的序列yj(j=xmin+d×k)，其中d是区间间隔，k=1，2，3，…，(R-xmax)/d。d值代表了此方法的分辨率。d值越小，分辨率越高，但同时也会导致计算量的增加，反之亦然。本文中，依据样本时间序列的特征，并经过定量分析确定极端阈值时取d为0.005。

(4)计算每一个新序列yj的长程相关性指数(DFA值，Dj)；

(5)当Dj的变化趋于平缓并收敛于数据的原始hq值时，则此时的j值即数据xi的极端事件的阈值。

2 数据选取与说明

本文以中国股票市场最具代表性的指数——上证指数为研究样本，原始数据选自上海证券交易所(SHSE)。上海证券交易所成立于1990年11月26日，并于1990年12月19日正式开始交易。上海证券交易所的营业时间为每个交易日的上午9:30到11:30，下午的1:00到3:00，每天共有四个小时的交易时间。本文所选取的数据即上证指数(SHSI)每日收盘价，但考虑到1996年12月26日之后，我国引入了涨停板制度，因此本文所选取的样本区间从1996年12 月 26 日(即涨停板之后)到2017年12月29日。我们的实证研究主要关注股票市场对数波动率(即收益率的绝对值)。

3 实证研究与结果分析

3.1 基本统计分析

图1列示了1996年12 月 26 日到2017年12月29股票价格指数(SHSI)的变化趋势，表1给出了该时间段内波动率序列的基本统计量。从表1中可以看出：波动率序列的偏度均大于0，说明其分布

呈右偏状，即波动率序列出现正值的概率大于收益率出现负值的概率；波动率序列的峰度都大于3，说明该序列不服从正态分布，而具有尖峰态特征。

3.2 股市波动率的长程时间关联分析

运用DFA方法对上证指数波动率序列的长程时间关联特性进行分析，其中s从10取到N/2，做出整个时间序列的二阶降趋势波动函数F(s)后，分析F(s)的对数曲线与s的对数曲线间的线性关系，如图2 所示。从图2中可以看出，F(s)与s之间存在显著的线性幂律关系，标度指数为0.89。由于α>0.5，我们可以得到如下结论：上证指数波动率序列存在长程时间关联特性，即上海股票市场存在着长期的持续性的演化状态，时间序列后一期数值会随着前一期的上升而上升，随前一期的下降而下降，呈现追随趋势的倾向。因此，可以根据这种市场固有的长期记忆特性找出波动率序列的有关规律。

图1 上证指数原始数据随时间变化趋势

表1 波动率序列的基本统计量分析

图2 上证指数波动率消除趋势(DFA)分析结果

3.3 金融市场波动率极端阈值的确定

在对金融市场波动率极端阈值进行确定时，考虑到金融市场极端波动事件是金融市场演化的极端状态或受到外界扰动而导致的异常状态，而金融市场的长程相关性不受或很少受极端状态的影响，因此可以运用DFA方法，通过确定序列的DFA指数何时开始收敛于原始值来确定极端波动率阈值。运用2.1及2.2中介绍的确定阈值的方法对样本区间内的数据进行实证研究，图3列示了DFA值的变化。从图3可以看出样本区间波动率极端阈值的定义过程及结果，样本区间内波动率极端阈值约为0.077。进一步地，根据DFA方法确定的阈值，可以得到样本区间内发生极端波动事件的具体信息，结果如表2所示。表2分别给出了发生极端波动的年份、具体时间、波动率、年度频次及平均强度。从表2可以看出：(1)在样本区间内，从极端事件的发生频次来看，共发生极端波动事件18次，其中2008年和2015年发生次数最多，达到4次，其次为1997年及2007年，分别发生2次，1998—2002年、2005年分别发生1次，2003、2004、2006及2009—2014年、2016—2017年未发生极端波动事件；(2)从极端波动率的强度来看，强度较大的年份分别为1997年、2001年、2007年、2008年及2015年。从上述实证结果可以看出，无论是从极端事件的波动率强度还是从发生频次来看，1997年、2007年、2008年及2015年都发生了金融市场的极端波动，这与1997年亚洲金融危机、2008年美国次贷危机及2015年中国股市发生的股灾等现象是相符的。

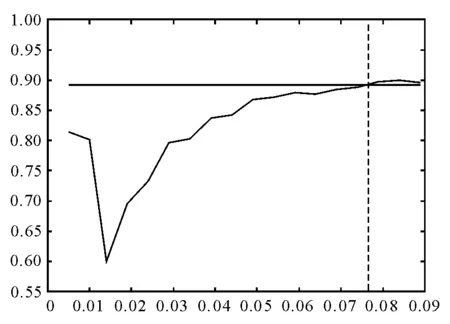
图3 样本区间内极端波动率阈值的确定

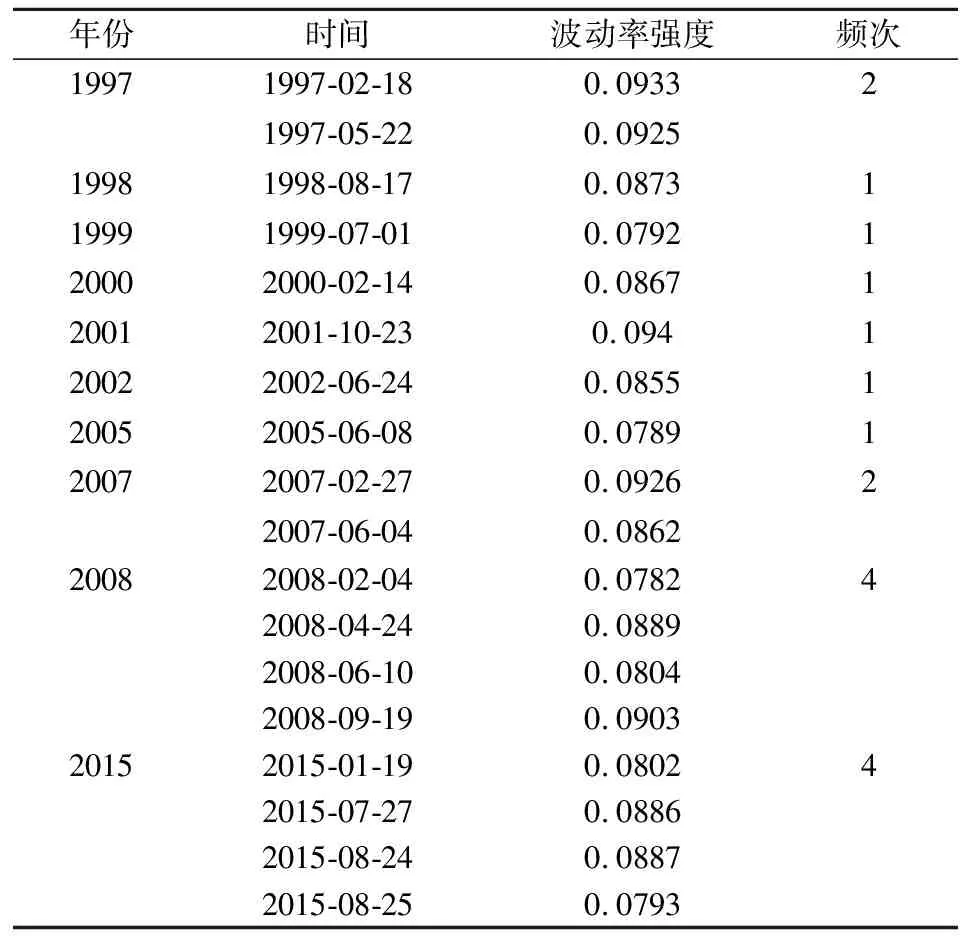
表2 波动率极端波动事件的具体信息

3.4 极端波动率的严重度分析

然而，单一地分析某一市场极端事件发生的频次或强度，往往不能准确地表征极端事件的严重度。只有在该市场极端事件发生次数较多并且强度也较大时，才能较准确地说明该市场发生极端事件比较严重。本文利用Du等提出的严重度指数对我国股市极端波动事件发生的严重度进行实证分析，该严重度指数的具体定义如下：

步骤一：对于极端波动事件，首先计算所有时间段上(年份)的极端事件发生的频次(Xi，i=1，2，3，…，n)，并且同时计算整个时间段内每一年极端事件超出阈值的平均强度(Yi，i=1，2，3，…，n)，其中n代表年份，即

Y=[(P-Pthreshold)/Pthreshold]×100%

(6)

其中：P是极端波动率的值；Pthreshold是极端波动率的阈值。

步骤二：将极端波动率的频次及强度进行标准化，则其值的范围为0～1，也就是

xi=(Xi-Xmin)/(Xmax-Xmin) (i=1，2，3，…，n)

1.1.1 药物因素 在治疗过程中，急性髓系白血病采用DA、MA和HA方案，急性淋巴细胞白血病多采用VDCP、VDP方案，非霍奇金淋巴瘤多采用CHOP方案，多发性骨髓瘤多采用VAD方案。使用阿糖胞苷、柔红霉素、足叶乙甙、米托蒽醌、表柔比星、环磷酰胺、长春地辛、左旋门冬酰胺酶等抗肿瘤药物［3］。因此，化疗药物抑制了患者口腔黏膜上皮细胞内DNA的复制和细胞增生，导致基底细胞更新障碍，引起黏膜萎缩，胶原断裂，形成口腔黏膜溃疡［4］;化疗后骨髓造血功能受抑，常伴有中性粒细胞减少或血小板减少，使口腔易发生感染或口出血，且常发生于两颊部和齿龈部［5］。

(7)

及

yi=(Yi-Ymin)/(Ymax-Ymin) (i=1，2，3，…，n)

(8)

其中：Xmin和Xmax分别代表了所有年份中极端事件发生的最低和最高频次；Ymin和Ymax分别代表了所有年份中极端事件的最低强度及最高强度。因此，xi及yi分别表示为标准化后的频次和强度。

步骤三：求出每一年的严重度指数。

EPSI=k1×xi+k2×yi(i=1，2，3，…，n)

(9)

其中，k1及k2分别是影响严重度指数的频次及强度的权重系数，k1+k2=1。由于强度及频次对严重度指数都具有影响，因此，本文中k1、k2均取0.5。此外，严重度指数的值应为0～1。

表3 上证指数极端波动率年度严重度指数

4 结论

针对当前极少对金融市场极端波动阈值进行研究的现状，本文以上证指数为研究对象，基于复杂性研究视角，以DFA方法为基础，运用DFA方法来确定金融极端波动率阈值，研究结果发现：

(1) 对股市波动率的长程时间关联进行分析，发现上海股票市场存在着固有的长期持续性的演化状态，时间序列后一期数值会随着前一期的上升而上升，随前一期的下降而下降，呈现追随趋势的倾向。因此，可以根据这种市场固有的长期记忆特性找出波动率序列的有关规律。

(2) 运用基于DFA的极端事件阈值确定方法确定了上海股市极端波动率的阈值，进而测算了股市极端波动的年度严重度指数，结果发现上述研究方法在研究股市极端波动时具有较好的应用效果。

本文基于复杂性研究视角，运用一种新的复杂性方法——DFA对极端波动率阈值进行确定。DFA 方法以系统动力学为基础，利用变换前后金融时间序列的长程相关指数变化特征来确定极端波动率阈值。与常规方法相比，该方法原理可行，计算出的阈值结果唯一，能较好反映金融极端波动率序列的统计效应和机理，在金融市场极端波动研究中具有很广阔的应用前景。本文只是运用复杂性方法对极端波动率阈值进行研究的一种尝试，后续深入的关于金融极端事件的定量化研究还有待进一步深化和完善，这也是我们后续努力的方向。