力学超材料的构筑及其超常新功能
2019-02-25于相龙
于相龙,周 济
(1.中国科学技术大学 中国科学院材料力学行为和设计重点实验室,安徽 合肥 230027)(2.清华大学材料学院 新型陶瓷材料与精细工艺国家重点实验室,北京 100084)
1 前 言
自然材料的力学性能,一般不是由一种属性、几种晶体学属性的总和,或是一系列的晶界工程特性决定的,而是由材料各组分或各结构单元之间的本构关系决定,即由不同单元之间组合的结构模式决定。相应地,其外在宏观表现出来的力学行为特征在工程中发挥着其应有的使用价值。基于此,超材料尝试着解除自然材料组分的影响,突出强化人工原子(单元格)几何构筑方式的作用。也就是说,通过对模块化的人工原子进行周期性或非周期性的几何结构优化设计来构建新型材料。这样得到的结构材料宏观呈现出的等效力学性能,可以由设计者按照需求自由选择、自由调整,创造出自然界前所未见的反直觉超常力学特性。
超材料具体指的是由人工微结构单元组成的功能材料,这些结构单元决定着超材料的宏观属性[1]。因此,超材料研究是多学科跨界融合的有力体现。不同研究领域之间的思维冲突与碰撞,唯有在相关学科之间的界限处才最能突显。超材料本质上源自于深入地理解电磁波如何与亚波长尺度散射结构相互作用,而后相继拓展到其他不同基元,从而可以实现许多自然材料没有的力、热、声、光等特殊性质和超常功能[2]。根据超材料所调控基元的不同,可将其分为光学超材料、声学超材料、热学超材料和力学超材料等。更广义地讲,光子晶体、声子晶体、光学超晶格、声学超晶格等人工微结构材料也可以纳入到超材料的范式之中。不过,目前除光学超材料的研究比较深入,其他类型超材料的研究依然处于起步阶段。
将超材料的设计理念拓展到力学领域后,成为了新型力学功能材料的生长点[3]。随着3D打印等先进制造技术的发展,具有更多样化、更新奇力学特性的力学超材料物理模型也不断地涌现。力学超材料是为调控弹性波而设计的人工微结构,以实现新奇的力学超常特性。本文依据各种不同类型力学超材料的几何结构特点,重点论及在人工几何构筑方面的基本情况,以及不同构型与超常力学性能之间的联系。在论述相关问题时,着重理清基本概念和基础理论,同时联系了具体事例,评述了力学超材料前沿研究领域的发展。
2 力学超材料的定义与范畴
力学超材料(mechanical metamaterials)或译为机械超材料,或称结构型超材料(structural metamaterials),是超材料研究领域的新兴分支,主要通过三维空间中特定的人工微结构设计来获得均匀材料所不具备的超常规力学性能[4]。新奇的力学超常特性不仅受限于构成该人工功能材料的组分,还强烈依赖于微结构人工原子/基元和几何结构的排布形式。力学超材料是一种具有超常力学性能的人工设计微结构,其单元特征尺寸范围在十几纳米到几百微米,整体结构尺寸为厘米级或更大[5]。
力学超材料种类繁多,极具代表性的力学超材料通常与3种弹性模量和泊松比这4个弹性常数有关。其中,杨氏模量E、剪切模量G和体模量K从工程角度分别可用于衡量材料的劲度(stiffness)、刚度(rigidity)和可压缩性(compressibility)。这些基本的力学性能参数也将作为力学超材料的分类依据。为此,按所调控弹性模量(杨氏模量、剪切模量和体模量)的不同,力学超材料可分类为负泊松比拉胀材料、剪切模量消隐五模式反胀材料、负压缩性材料、负热膨胀材料、模式转换可调刚度材料、低密度超强仿晶格材料、折纸/剪纸超表面材料等[6-8]。本文未涉及折纸超表面材料,也未具体论及面向3D打印力学超材料的制备技术,相关内容可参见书籍文献[9]。
目前存在两种力学性质图可以作为力学超材料设计的主要分类依据,这两个基本图表绘制了各种力学性质的组合[10]:一是杨氏模量与密度(E-ρ)图,称为Ashby图[11, 12],用于评估轻质超强力学超材料;二是体模量与剪切模量(K-G)图,其中节选第一象限的部分,称为米尔顿(Milton)图[13]。
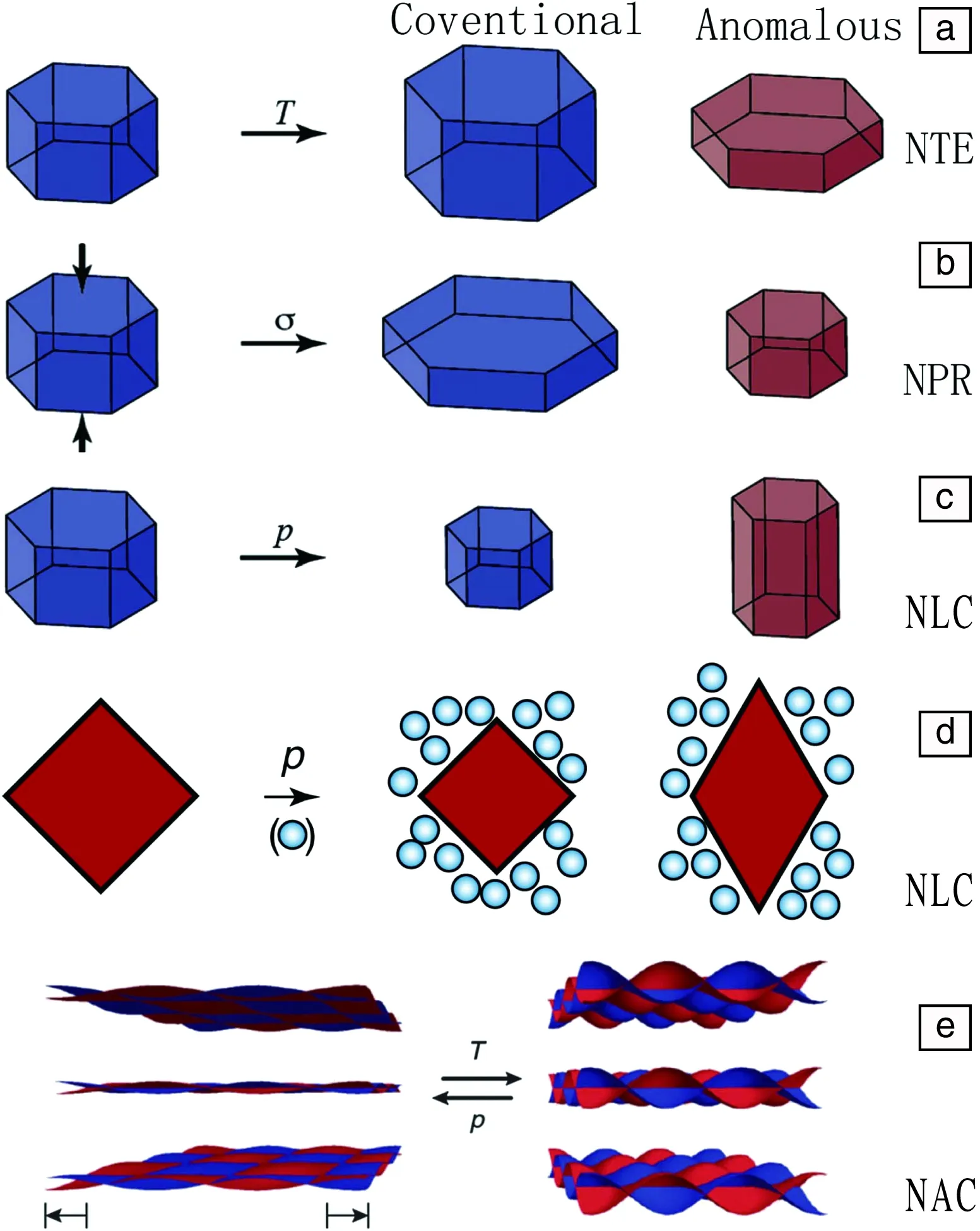
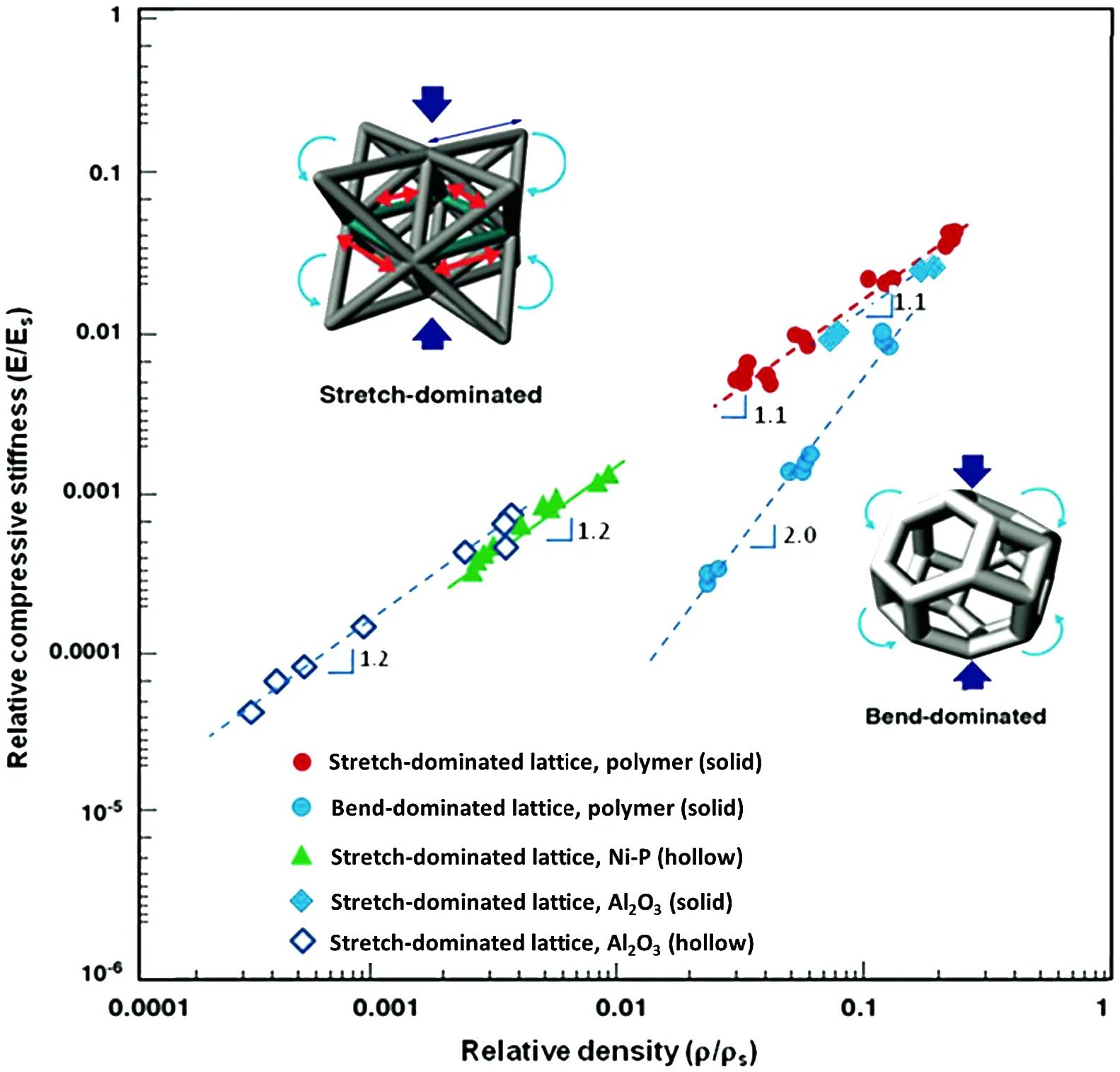
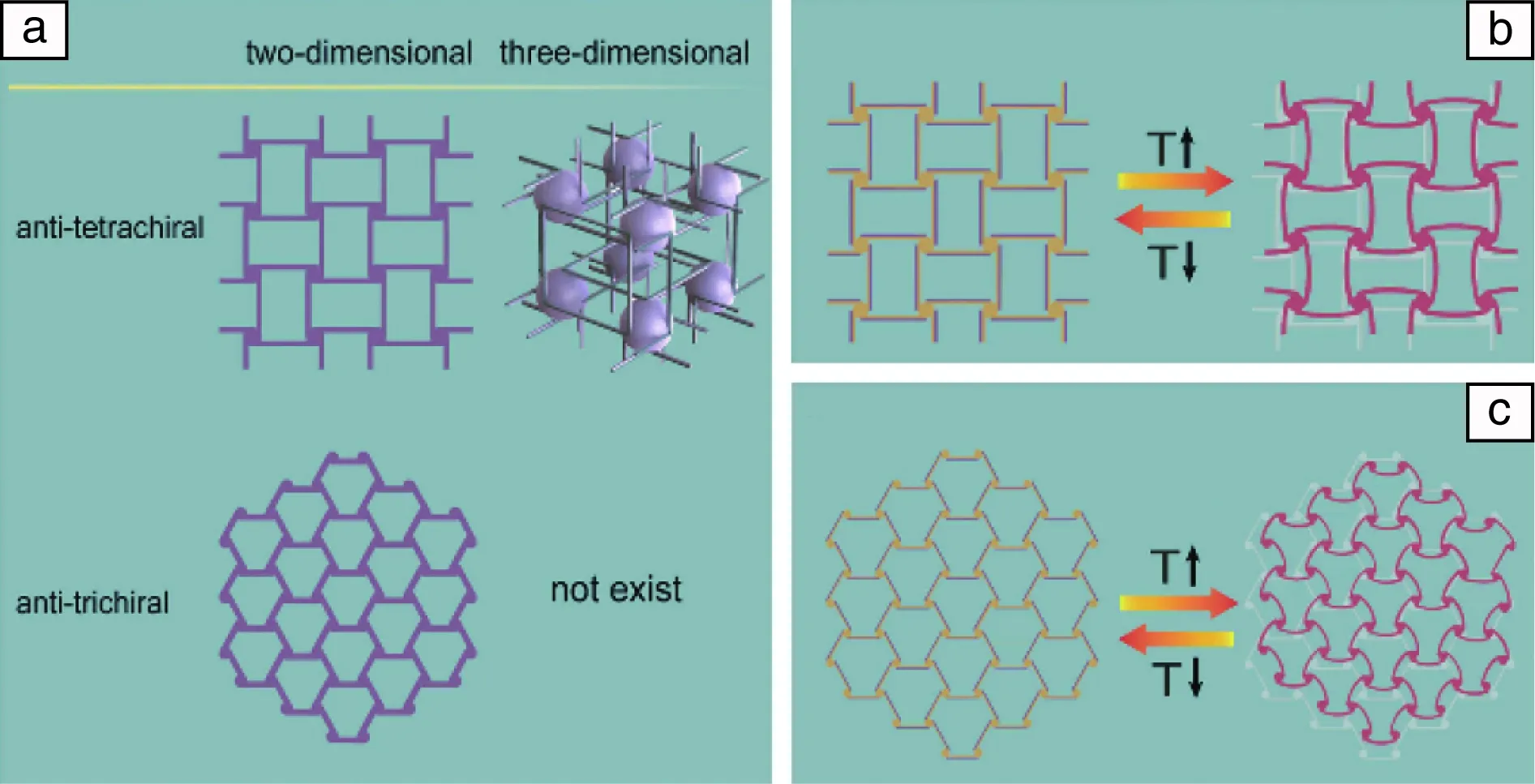
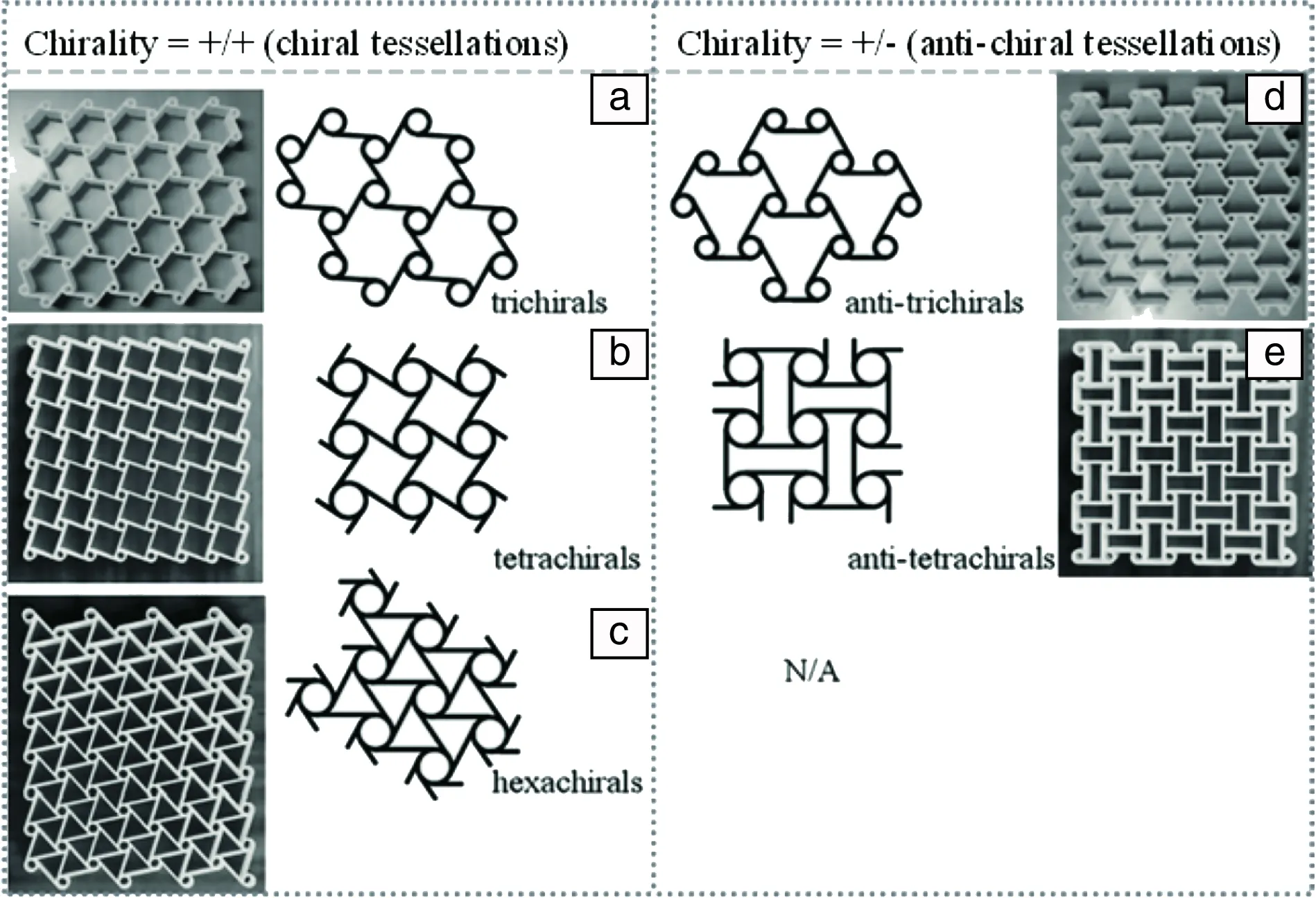
如图1所示,在米尔顿图中包括3个主要的区域范围[4]。第一个典型区域是G(x)轴,为泊松比为负值的拉胀力学超材料。第二个典型分布区间落在K(y)轴,剪切模量接近于零的情形,是剪切模量消隐的反胀材料。第三部分是位于右下角的第四象限,满足E>0和-4G/3 图1 扩展米尔顿K-G图及力学超材料分类[4]Fig.1 The K-G map, correlation of the bulk modulus K and shear modulus G with the Poisson’s ratio and stability[4] 力学超材料呈现反直觉的超常力学行为主要有:泊松比为负值的拉胀行为、剪切模量与体模量相比很小的超流体行为、剪切模量为负值的负可压缩性、杨氏模量可调节的模式转换双稳态特性、低密度高强度的仿晶体缺陷模式以及其热膨胀系数为负值的负热膨胀行为。 负泊松比(negative Poisson’s ratio,NPR),是典型的拉胀力学超材料的超常力学性能,是指一类人工结构功能材料在被拉伸时横截面会变得更膨胀。从力学意义上来说,其泊松比小于零(v<0),或在体弹性模量与杨氏模量之比远远小于1(K/G<<1)的相对极限时,泊松比约等于-1,对应于米尔顿图1中的G(x)轴。有时也可用“Auxetics”来指定人工设计的这种新奇力学属性。 根据不同的人工原子结构样式,人工设计的负泊松比数值具有相对广泛的存在范围,直至-20,如图2所示[4]。这些力学超材料结构包括嵌入式凹角结构、类似聚氨酯泡沫塑料制备的向内折叠分组多孔结构、旋转式方形或三角形铰接结构单元、手性和反手性结构、单元晶格或是球状几何结构、三维折纸结构以及金属纤维几何网络结构等。 随着负泊松比拉胀力学超材料研究的不断深入,更具多样化和个性化的几何结构不断出现,依据几何结构进行分类的方法也越发突显其局限。因此,可依据这些不同类型的几何结构设计背后的负泊松比属性,将负泊松比拉胀力学超材料分成两大类:一类是零或负泊松比,另一类是正负混合型可编译的泊松比。前者属于完全负泊松比,其材料结构的等效泊松比始终是零值或负值。而后者为部分负泊松比,有时泊松比数值为负,有时数值为正,这种正负混合型可编译部分负泊松比材料,同时共有正值泊松比和负值泊松比。什么时候超材料表现为正泊松比、什么时候是负泊松比,取决于人工原子结构本身在变形过程中的方向变化,类似于固体晶格结构中的不同晶粒的取向关系。 在图1所示的米尔顿图中,当力学超材料的剪切模量数值远远小于杨氏模量时(G< 利用双光子3D打印直写技术,可以制备这种五模式结构材料,如图3所示。图中基本的五模式结构单元是两个平头圆锥体由点接触对接而构成的双锥结构单元[15, 16]。相应的衍生几何结构包括具有不同直径和外径长度的非对称双锥结构单元,还有不同横截面形状如正三角形、正方形、五边形、六边形和圆形[17]。研究发现,三角形断面表面呈现出较好的声学隐身特性。总之,在双锥体几何结构基础上派生的代表性改进方式有:① 移动会合的接触点;② 改变双锥结构元件的对称性;③ 选择不同的锥体横截断面的形状;④ 调节两个连接圆锥体的直径范围;⑤ 探索圆锥体单元简化设计成铰接杆件。 图3 剪切模量消隐的五模式反胀力学超材料[16]:(a)整体外形,(b)上下直径不同相连接的双圆锥结构单元Fig.3 Pentamode metamaterials[16]: (a) oblique-view, (b) the magnified view for two connected truncated cones 压缩率可近似为体模量K的倒数,主要是指在静水压力作用下,固体或流体相对于其所受的压力变化而引起的相对体积变化的量度。通常情况下,材料压缩率为正值,仅在强椭圆限制条件时[18],存在极少数天然材料的压缩率数值可能是负的。负可压缩性指的是材料在受静水压力作用时经历膨胀过程,或在受拉力时其固有体积却产生收缩的现象[19, 20]。负压缩性结构材料与负泊松比拉胀材料有相似之处,都存在受压时产生膨胀响应的效应。不同之处在于,负泊松比拉胀材料是轴向压缩时侧面承受收缩效应,而负可压缩性结构是指随外界压力的变化,结构材料的相对整体体积改变量反直觉,具体区分参见图4。 图4 超常力学行为示意图:(a)负热膨胀,(b)负泊松比,(c,d)负线性可压缩性,(e)负面积可压缩性Fig.4 Conventional and anomalous mechanics for materials exhibiting: (a) negative thermal expansion (NTE), (b) negative Poisson’s ratio (NPR), (c, d) negative linear compressibility (NLC), (e) negative area compressibility (NAC) 负可压缩力学超材料是当杨氏模量大于零(E>0)时,满足-4G/3 负压缩力学超材料主要包括有一个方向上的线性可负压缩性和两个方向的面积可负压缩特性,分别对应于负线性压缩(negative linear compressibility,NLC)和负面积压缩性(negative area compressibility,NAC)。负压缩性力学行为主要来自于该领域最近化学研究的一些启示。负线性压缩性侧重于在拉伸晶体中的整体结构单向收缩[23];而负面积压缩性侧重于整体结构在两个方向上的收缩情形[24],如图4c和4d所示。 模式转换(pattern transformation)可调刚度(tunable stiffness)力学超材料指的是在外力变形条件下,给定的二维多孔软材料模板出现了一种可调节杨氏模量的力学行为。这种可切换受力模式的宏观力学行为,类似于大多数金属晶体材料科学中不同显微结构之间的物相转变过程(phase transformation)关系[25]。 如图5所示,该材料可以在外载荷作用下,从具有特定的周期性模板范式转变到另一种更大尺度的力学不稳定状态[26]。当这种材料被压缩到超过某个力学行为所要求的阈值时,会引起应力-应变特性宏观尺度方面状态形式的改变。从应力-应变曲线中可以推出弹性模型的正负变化过程,这种力学特性的转变,本质上是一种合作式的屈曲方式,使得超材料中的人工原子呈现出元属性(metaproperties)的不同。 图5 应变为0(a),-0.125(b),-0.25(c)时,左列圆形,中列十字形和右列星形结构直孔模板受力情况[26]Fig.5 Experimental images of structures circle (left), cross-shape (middle) and star (right) at different levels of applied engineering strain ε=0 (a),-0.125 (b) and-0.25 (c)[26] 典型的模式转换可调刚度材料主要是软材料构成的多孔板,如图5所示,可以等效为一种周期性的弹性胞状固体,不同之处在于该结构背后的设计理念是基于弹性材料的屈曲不稳定性。这种材料结构设计本质上是非线性的,因此在宏观应变数值相对较小时,可以在某些类别的简单周期性结构中引发剧烈变化。 可调杨氏模量力学超材料主要利用弹性材料的结构不稳定性,由力学拉胀而引起的材料响应软化、切线模量的衰减、可反转的弹性不稳定性去激发不同样式的改变。传统意义上的弹性不稳定性多被认为是缺陷模式。这种类型的超材料主要是利用几何结构的缺陷形式,类似于固体晶格结构中的点缺陷。不过,从本质上来说,可调力学超材料的内在特性表现为整体几何结构的刚度可调节性,类似于材料力学中压杆稳定的临界状态,是一种可以反转的弹性不稳定状态,从而引起了整体结构等效弹性模量的正负值变化。这类材料可被用于定制各种不同的力学属性,如可调或开关式负泊松比拉胀材料。 仿晶格构筑的微结构材料是依据自然晶体的理论学说、选用不同形状的人工原子(纤细梁或杆件)进行周期性或非周期性陈列成胞状、网格状、桁架式或晶格结构材料,从而可以制备与所选自然材料不同力学特性的几何结构材料。仿晶格和仿晶格缺陷的力学超材料可以表现出许多独特的材料属性和效应,较为常用且突出的力学特性是轻质结构时的超高强度。 轻质超强度力学超材料指的是在低密度下刚度、强度和韧性等诸多力学属性超强耦合的一种人工结构材料,其质量密度一般可选择在小于10 mg/cm3的范围[27]。目前,超轻超强(E/ρ)力学超材料可分为4类:① 分级式微纳晶格网状结构,② 手性与反手性几何结构,③ 用来模拟位错等晶格缺陷的折纸曲面折叠超表面材料,④ 折纸与微纳晶格结构结合而形成的晶格状折纸材料。仿晶格结构中,依据所构建晶格几何结构的不同,又分为5种类型:人工晶格结构、开孔泡沫结构、闭孔泡沫结构、六边形蜂窝结构和手性/反手性结构。 依据晶体学中的布拉格晶格结构,可以制备出任意刚性和非刚性纳米晶格拓扑结构,如图6所示[28]。其中包括八面体桁架结构、立方八面体结构、三维Kagome三角结构和四面体结构。这4种晶格拓扑结构中,具有不同程度的刚度和平均节点连通性(Z):① 八角形桁架(刚性,Z=12),② 立方八面体(周期性刚性,Z=8),③ 三维Kagome(周期性刚性,Z=6),④ 四面体(非刚性,Z=4)。晶格由固体聚合物和椭圆形横截面的空心Al2O3梁构成,并源于不同制造技术方法[29]。 图6 4种晶格拓扑结构[28]:(a)八面体桁架,(b)立方八面体,(c)3D Kagome,(d)四面体(图ii标尺=10 mm,图v标尺=5 mm)Fig.6 The four nanolattice topologies[28]: (a) octet-truss, (b) cuboctahedron, (c) 3D Kagome, (d) tetrakaidecahedron(the scales bars in ii) are 10 mm, and the scale bars in v) are 5 mm) 图7给出了弯曲和拉伸变形模式主导的胞状晶格结构的Ashby图[30]。这两类晶格结构的整体屈服状态源于内部结构单元的塑性屈服、弹塑性失稳或断裂,所有内部单元格塌缩压实后应力重新上升。拉伸变形主导胞状晶格结构的内部单元处于均匀拉伸状态,弹性应变能密度高,具有高屈服强度和屈服后急剧下降的力学行为特性。对于相对密度相同、弯曲变形占优的胞状晶格结构,弯矩导致结构单元发生局部受拉或受压屈服,因而屈服应力远低于拉伸主导胞状材料,屈服平台呈现出应力恒定的水平段。 图7 弯曲和拉伸主导晶格的Ashby图[30]Fig.7 Ashby figure for bending/stretch-dominated lattice[30] 由此可见,胞状晶格结构标度律与配位数密切相关。提高配位数意味着变形模式倾向拉伸为主,幂指数p,q减小并趋于极限值1。降低配位数将导致弯曲主导的变形模式,幂指数p,q增大,弹性模量和屈服强度随相对密度减小而急剧下降。海绵、蜂巢等常见天然三维胞状结构的配位数(约为3~4)低于临界值Z=2,结构单元以弯曲变形为主,杨氏模量和屈服强度通常较低。不过,若融合纳米晶格尺寸效应和超材料的几何结构设计,结果可能会有所不同。 负热膨胀(negative thermal expansion,NTE)行为是指当人工结构材料被加热时整体几何结构中出现一个方向或多方向的收缩效应(如图4所示)而冷却时膨胀,即热膨胀系数为负值。 负热膨胀超材料的几何结构通常是由热膨胀系数差异较大的两种或两种以上材料构成。由不同热膨胀系数的材料制成的几何结构,其单元格结构的热膨胀或收缩,可引起整体几何结构不同程度的弯曲变形[31]。负热膨胀超材料主要的拓扑结构有手性几何结构、三维六角形晶格的胞状泡沫多孔结构、旋转三角形或正方形结构以及盘形、圆柱形和针形夹杂物等[32, 33]。 极具代表性的负热膨胀几何结构单元是三阶手性结构单元,如图8所示。这种手性结构使用的是双材料肋梁元件,这些肋梁在温度变化时会出现弯曲,从而引起节点旋转,进一步引起整个网格结构应变的变化。通过在热板上加热这些肋梁结构,可以观察到其曲率半径的变化,从而确定高和低两膨胀侧的情形。 图8 双材料韧带反手性负热膨胀超材料(a),四阶反手性(b)和三阶反手性(c)材料在热作用下的变形状态图[34]Fig.8 Antichiral NTE models (a), deformed anti-tetrachiral(b) and deformed anti-trichiral (c) under thermal stress[34] 利用双材料或是多材料组成的几何结构,调整结构的曲率变化来进行负热膨胀系数的优化设计,可以组合形成各种各样的力学超材料类型。可以变换组成材料的成分,或者变换所构建材料的结构单元排布。例如一种由角铰状梁状元件组成的三角形结构:每个组成元件有其固有的热膨胀系数,其中一个具有相对较大的热膨胀系数[35]。将该结构单元细分为更复杂的结构,在温度变化时,可以使三角构型内的不同结构单元产生不同程度的拉伸或压缩扩展,从而表现出不同于组元自身的热膨胀系数。这种由多种材料几何构建而成的整体材料,表现为整体等效的负热膨胀系数,但这并没有改变组成这种几何结构材料的单个材料的热膨胀系数。负热膨胀力学超材料设计的关键在于两点:一是自然材料热膨胀系数的差异性选择,二是选择适合的几何结构拓扑样式。通过调整几何结构和材料属性之间的给定关系,有效调节负热膨胀系数的可选择范围。 需要特别指出的是,将负热膨胀超材料归为力学超材料而不是热学超材料,这主要是依据具体的材料结构设计机理来划分的。因为热学超材料主要是通过调整热流来设计材料结构,而负热膨胀超材料本质上是利用在受热过程中几何结构单元的受力变化而实现胀缩,这里的热源只是作为触发几何结构发生力学变形的外在条件,而不是主要调节规划的参数。负热膨胀超材料在这一点上与热学超材料调节热流参数存在本质上的不同。 一般情况下,通过梁柱矩阵方法分析的晶格结构类型包括方形网格、三角形网格、六边形蜂窝、分级六边形蜂窝结构和三阶手性蜂窝结构,如图9所示[36, 37]。图中角度θ给出了三阶手性晶格中直壁的取向。 图9 晶格结构类型[36]:(a)方形,(b)三角形,(c)六边形蜂窝,(d)分级六边形蜂窝,(e)三阶手性Fig.9 Types of lattice structures[36]: (a) square grid, (b) triangular grid, (c) hexagonal honeycomb, (d) hierarchical hexagonal honeycomb, (e) trichiral honeycomb 以模式转换刚度可调力学超材料为例,完美多孔胞状结构材料中的周期性弯曲图案模式在受外力作用下而形成塌陷表面,则在其下面的微结构中会不可避免地包含晶格缺陷,相应的组成材料中就会发生应力失效。其中几何结构的屈曲应力可以量化,以获得二维胞状几何结构中的一些初始失效的上边界。 为了研究节点连通性,可以模拟由均直和均匀的梁(相同的横截面和材料)制成的不同二维规则网络的力学行为。通常需要了解多种不同的人工晶格几何结构网络,以检查连通性和无序性对力学性能的影响。3个常规的人工结构晶格:六边形(连通性Z=3),kagome(Z=4)和三角形(Z=6);以及两个无序的栅格:Voronoi(Z=3)和Delaunay(Z=6)网络。 “手性”(chiral)几何结构,可以被构筑成为“左手”或“右手”结构材料。无论是左手或是右手,皆为非超可变的镜像图像。手性几何结构单元网络的每一个单胞是由一个称为节点的中心圆柱体组成,圆柱周边存在6个切向连接的韧带,展现出六阶的旋转对称性,其完整描述可参见图10六阶结构单元[38, 39]。 图10 平面手性结构单元的周期排布[38, 39]:(a)三阶手性,(b)四阶手性,(c)六阶手性,(d)三阶反手性,(e)四阶反手性Fig.10 Five chiral tessellations and their rapid prototypes[38, 39]: (a) trichirals, (b) tetrachirals, (c) hexachirals, (d) anti-trichiral and (e) anti-tetrachiral 由圆柱中心体和连接杆件所构成的连接结构,组成了基本的手性结构单元。一个圆柱中心体上可以连接3、4、6个连接杆,分别称为二阶、四阶和六阶结构单元。这些不同阶数的几何结构单元,再通过手性或反手性的平面周期性排布,就形成了手性或反手性系统。当连接杆件位于两圆柱体内切线方向布置时,也就是说圆柱体在连接杆的两侧,可以归属于手性系统,如图10a~10c所示。当连接杆件位于两圆柱体外切线方向布置时,也就是说圆柱体在连接杆的同一侧,可以归属于反手性系统,如图10d和10e所示。在生物医药研究领域的反手性体系中,当具有等量的左手和右手基本单元时,可以形成外消旋。将相对较薄的韧带焊接到节点上,单轴的轴上载荷将导致节点的旋转,伴随着韧带的弯曲。因此,当蜂窝周期排布几何结构体系承受压缩载荷时,这种变形可能导致节点周围的韧带折叠,当受到拉伸载荷时会产生展开,几何结构内部的相互作用,使得整体结构的拉伸性增强。 需要说明的是,目前超材料的几何构建方法很多,大体可以归类为人工晶格结构的规则设计和手性结构的非规则设计。规则与非规则两大类足以涵盖力学超材料几乎所有的几何构建类型,典型的结构设计都可以归为这两个组类。衍生的子类也很多,这是很庞大的两大规则与非规则几何结构设计体系,本文阐释时不可避免地呈现了不同程度的简化,希望后续的研究工作能在不同层面上继续拓展。 本文简要地将种类繁多的力学超材料进行了系统性的分类,并扼要地论述了其超常的力学性能。基于人工晶格结构和手性/反手性几何结构单元,可以构筑具有反直觉超常新颖的力学特性,包括负泊松比的拉胀行为、剪切模量消隐的超流体、负剪切模量的负可压缩性、杨氏模量可调节的双稳态模式转变、轻质超强的仿晶格缺陷和负热膨胀行为。对于每种类型的力学超材料,主要阐述、理解了一些基本概念和超材料设计理念。针对反直觉超常的力学行为,着重关注了这些几何结构上更具有概括性和普通性的部分。从而,可以立足于其中一到两项力学行为研究的基础,将视线看得更远一些、更广一些。 需要指出的是,3D打印制备力学超材料技术带来了新的挑战和机遇。协同超材料几何优化结构和微纳米材料多尺寸效应,二者的融合将有望实现更多更新颖的未发现的力学属性,可以预见:① 在今后的研究过程中,不同形式单元格排布的相互耦合会使得整体结构更加复杂化、多样化和个性化;② 以后的几何结构构建时,将更加侧重于改变单一组分材料的构成方式,会出现两者或两者以上多种不同材料种类的复合制备;③ 在基础理论研究方面,将会更深入地引入固体力学稳态梁或板壳基础理论,例如双稳态和多稳态方式构造模式转换可调刚度力学超材料。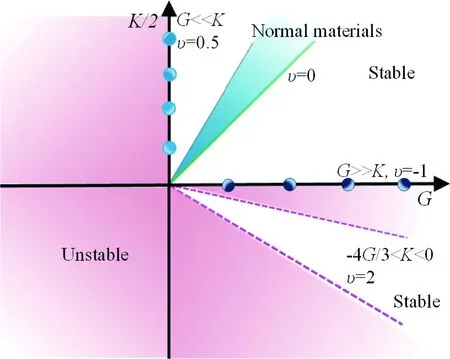
3 力学超材料的超常力学性能
3.1 负泊松比的拉胀行为
3.2 剪切模量消隐的超流体

3.3 负剪切模量的负可压缩性
3.4 杨氏模量可调节的双稳态特性

3.5 轻质超强仿晶格缺陷

3.6 负热膨胀行为
4 力学超材料的几何结构构建
4.1 人工晶格结构

4.2 手性与反手性几何结构
5 结 语
