某型火炮不同模块装药弹带挤进过程的数值模拟

孙 鹏，刘东尧

(南京理工大学动力工程学院， 南京 210094)

在经典内弹道理论中，为简化模型忽略弹丸的挤进过程，将弹带从开始变形到完全进入膛线假设为瞬态过程，设定一个确定的挤进压力作为弹带完成挤进并开始运动的启动压力。经典的内弹道模型及数值计算表明，不同的挤进压力对内弹道参数产生较大的影响。这是因为这种假设与弹带实际的挤进过程存在着很大的差别，因此，瞬态挤进不利于完整精确地刻画装药点火及开始着火燃烧阶段的内弹道特性。随着科技和研究手段的进步，研究人员发现弹带的挤进过程是一个材料的高速挤压成型过程，具有高瞬态、高应变率和大变形等特点。

本文研究的某型大口径炮采用模块装药，不同的模块装药由于膛内压力上升过程的差异会对弹丸的挤进过程及内弹道性能产生影响。很多学者对弹带挤进过程进行了理论分析、实验研究和有限元仿真等研究。金志明[1]在经典内弹道学研究中研究了挤进过程的挤进阻力，其将挤进阻力分为动态载荷作用下的内耗产生的阻力和材料变形产生的阻力两部分并且给出了考虑挤进阻力的弹丸运动方程。但是由于动态过程的复杂性，对公式中的阻尼因子难以进行定量描述，只能依靠试验来获得该参数的有关数据。后来研究人员提出了准静态及动态挤进模型。根据前倾角和坡膛角的大小关系分两种情况确定阻力随位移关系曲线[2]。Chen P C使用ABAQUS模拟了弹带的挤进过程，在研究过程中假设身管和弹丸为刚体且内膛光滑对称，计算得出仿真过程中弹带和身管的接触力并进行分析[3]。Keinanen H[4]和Toivola J[5]采用简化的模型研究了弹带在光滑身管内的挤进运动过程，测量了由于弹带的挤进在身管表面产生的应力，认为弹带材料和结构的变化对身管磨损和烧蚀起主要作用。孙河洋[6-7]建立了身管和弹带的三维模型并对弹带挤进过程进行了仿真，使用初始损伤及累计损伤模型建立内弹道模型研究了坡膛结构变化对挤进过程以及整个内弹道过程的影响。孙全兆使用ABAQUS有限元分析软件对初始内弹道中的动态挤进阻力和挤进压力的问题进行了研究，分析研究了弹带材料大变形及断裂失效模式[8]。王鹏研究了不同弹带材料对挤进过程影响的机理，并且提出了新型塑性弹带材料的研究方向[9]。李淼认为摩擦力随着弹带滑动变化，并且在切应力模型中考虑了材料的剪切极限，使用ABAQUS对弹带挤进过程的挤进阻力进行研究分析[10]。

对于大口径火炮的模块装药，在不同的装填状态下，由于装药条件的差异，弹带挤进阶段膛内的压力将发生较大的变化，会影响到弹丸内弹道过程中的参数。

为研究不同模块装药条件下弹带挤进过程的影响规律，本文使用ABAQUS建立了某型火炮弹丸挤进身管的三维模型，引入Johnson-Cook本构模型描述弹带的塑性变形，载荷的加载使用内弹道方程组与挤进过程耦合方法，具体方法参考文献[6-7]。采用非线性显式分析的方法研究不同模块装药条件下某型火炮的弹带挤进过程的运动及变形规律。

1 物理模型

本文研究的某型大口径榴弹炮的弹带的结构见图1，主弹带与身管之间有很小的弹带强制量。火炮射击前，先将弹丸在坡膛中装填定位。此时弹带凸台与坡膛紧密接触，后弹带的凸台可以更好的密封身管内的火药燃气，提供更好的内弹道性能。火药开始燃烧后，弹丸受弹底燃气压力作用，克服挤进阻力向前挤进，弹带在膛线和身管的挤压下发生塑性变形产生凹槽，等到弹带部分全部挤进膛线，整个挤进过程结束。

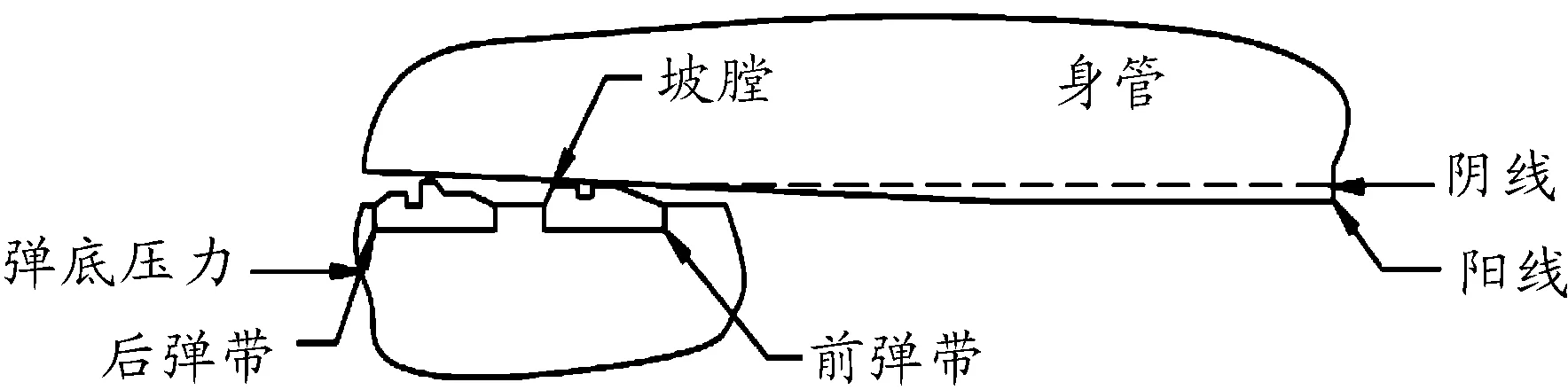
图1 弹丸挤进过程示意图

2 有限元模型

1) 模型假设

弹带在挤进过程中的塑性变形很大，受力十分复杂，使得仿真很难继续。为了可以通过数值模拟得到预期的结果，因此我们对弹带的挤进过程做出如下假设：

① 规定以装配完成时弹带和身管的相对位置作为挤进过程的开始位置，假定弹带的初始应力和初始变形为0。

② 对身管和弹体施加刚性体约束，仅考虑弹带材料的变形，忽略身管和弹丸本体的应变。

③ 不考虑弹丸的动不平衡，假定炮弹质心与火炮身管的轴线共线。

④ 不考虑挤进过程中身管的后座运动、忽略弹丸前端空气阻力以及重力。

⑤ 假定弹丸与身管没有热交换，挤进过程中弹带材料的变形是绝热过程。

2) 网格划分

本文中对于弹带、弹丸和身管的网格选择采用六面体减缩积分单元。由于本文主要的研究对象为弹带，不考虑弹丸和身管的变形，因此对弹丸和身管进行了刚性体约束。弹带部分的网格单元比较密，为了提高计算效率的同时保证计算精度，弹带网格采用八节点六面体减缩积分单元，对于弹带使用细化网格本文分别建立了0.3 mm、0.35 mm、0.4 mm、0.45 mm和0.5 mm五种不同网格尺寸的弹带有限元模型进行试算。对五种不同的网格进行网格尺寸敏感性分析之后选取0.35 mm作为弹带网格的基本尺寸。由于假设弹丸和身管是刚性体，因此对其建模时选择了较大的网格尺寸。

其中弹带的网格模型如图2所示。

图2 有限元网格模型

3) 材料模型

为了描述弹带在数值模拟中出现的大塑性变心、损伤、应变硬化、应变率硬化以及温度软化等现象，本文引入了Johnson-Cook本构关系模型来描述，可以很好地描述出材料在大应变、高应变率和高温下的塑性变形和断裂失效。Johnson-Cook本构关系模型包括分别用以描述塑性变形和断裂过程的Johnson-Cook塑性模型及损伤失效模型。

在Johnson-Cook塑性模型中假定弹带材料是各向同性材料并且符合Von Mises屈服条件。屈服应力用以下公式表示：

(1)

(2)

(3)

弹带采用Johnson-Cook初始损伤准则，使用等效塑性应变定义初始损伤[11]：

(4)

式中：D1～D5为材料断裂失效参数；σ*为应力三轴度。

4) Mie-Gruneisen状态方程

本文数值模拟中弹带变形中的应力应变被分解为体积项和剪切项。其中弹带材料的塑性变形行为由Johnson-Cook塑性本构方程描述。与体积项相关的静水压力由Mie-Gruneisen状态方程[13]描述。

材料受压缩时，Mie-Gruneisen状态方程定义了材料的静水压力：

(γ0+aμ)E

(5)

材料膨胀时，Mie-Gruneisen状态方程定义了材料的静水压力：

p=ρ0c2μ+(γ0+aμ)E0

(6)

式中，c是体积声速；S1、S2、S3是曲线的斜率系数；γ0是Gruneisen Gamma系数；a是对γ0的1阶体积修正；E0是初始单位体积能；ρ0是材料初始密度；μ用下式表示：

(7)

5) 载荷及边界条件

驱动弹带挤进的载荷采用内弹道方程组与挤进过程耦合求解算法[13]。可以使用ABAQUS中的幅值子程序接口Vuamp实现。将经典内弹道方程组联立消元可得下式：

(8)

(9)

其中，Z是火药颗粒相对已燃厚度，v是弹丸速度，a是弹丸加速度，l是弹丸行程，t是时间，其余是内弹道参数。上式中共有Z、v、a、l四个未知量，使用FORTRAN编程。火药完成点火后，设定一个很小的Z作为初始扰动采用龙格-库塔法计算得到初始扰动p，此时弹丸在初始压力的作用下开始运动。在ABAQUS中计算弹带的运动及变形，得到弹丸的行程、速度和加速度等参量。之后利用FORTRAN和ABAQUS进行循环计算，具体步骤为将仿真得到运动参数以及显式非线性有限元求解器提供的时间步长代入上式求解得到时间步长n结束时刻对应的膛压p，循环上述过程直至仿真结束。

对身管和弹丸本体施加固定约束的边界条件。

3 计算结果分析

3.1 弹带形态变化分析

弹带在四种装药号载荷作用下的挤进过程经历了相似的形态变化过程，但是不同工况下挤进运动参量存在差异。首先以一号装药条件下弹底压力数据作为模型的载荷对建立的模型进行数值计算。从结果可得出在挤进过程中弹带材料的变形规律和分析刻槽的形成机理。图3显示了弹带挤进过程中不同时刻的应力分布和发展情况。

由图3可见，在挤进开始后，弹带向前运动，在3.5 ms时后弹带凸台与坡膛接触，在接触面上发生应力集中现象，前弹带发生塑性变形并被挤入后弹带的凹槽。随着挤进过程的继续前弹带在4.5 ms开始接触坡膛，发生塑性变形，并且开始嵌入膛线，之后随着弹底压力不断增加，弹带挤进速度也随之增加，在5.25 ms时前弹带完全挤进膛线。随后在5.5 ms时后弹带开始接触膛线并发生相互作用，在这个过程中弹带材料继续发生塑性变形，在挤进过程中弹带过盈一部分被膛线挤压至弹带后面的凹槽，弹带与阳线接触部分一部分被挤压到弹带后方，另一部分被挤入阴线槽内。弹带单元定义了韧性损伤模型，在挤进过程中当材料参数达到了设定的损伤值时，该单元便发生失效被删除。当弹带完全挤进身管时，挤进过程结束。

孙全兆对该型大口径榴弹炮弹带进行了挤进试验研究。测试了弹带在一号模块装药条件下的挤进参量。为了便于试验使用了截短身管进行试验对于挤进过程中的压力采用压电式压力传感器通过数据采集系统来记录试验中的压力信号。使用高速摄像技术测量弹丸的位移、速度等运动参量。试验值和仿真值的对比结果如表1。

由对比结果可知弹带刻槽的数值模拟结果与实测结果大致符合，但是在数值上整体偏小。这是因为在试验的时候使用的是截短身管，因此弹带在挤进过程结束之后还会在身管运动一段距离，加剧弹带磨损。弹带运动参量的数值模拟值比试验值稍小，但误差在可以接受的范围内。因此可以认为弹带在挤进过程中弹带位移和速度响应的数值模拟结果和测试结果有很好的一致性。弹带数值模拟的挤进阻力与试验值的差距较大，达到了3(105N。由于挤进过程受弹带材料、形状、以及材料本构关系等多种复杂因素的影响，会不可避免地出现误差。通过对比分析表明，大口径榴弹炮弹带挤进过程的数值模拟与试验结果具有很好的一致性，说明本文建立的弹带挤进过程仿真模型符合实际，可以很好的描述弹带的挤进过程。

3.2 不同装药条件下弹带运动结果对比

在一号装药条件下弹带挤进过程计算和分析的基础上，改变弹底载荷对不同装药量弹带的挤进过程进行了数值仿真，探究装药号的变化对挤进过程内弹道参数的影响。图4-图7分别给出了不同装药条件下弹带挤进过程中的位移-时间、速度-时间、加速度-时间和挤进阻力-弹丸行程关系曲线。本文四个模块装药号中一号装药的药量最大，四号装药的装药量最小。

由图4的弹带位移-时间曲线可见，随着模块装药装药量的增加，弹带完成挤进过程所需的时间减少，一号装药工况的挤进时最短只有6.8 ms,四号装药工况的挤进时间最长，达到了10.52 ms。图5给出的弹丸挤进速度曲线表明，挤进过程中装药量越大，弹丸的挤进速度越大，这符合实际物理规律。进一步观察弹带挤进速度时间曲线可以看出，随着装药量的减少，弹带的挤进速度先增加，在某一时刻开始速度增加速率下降，随后速度继续增加直至挤进过程结束。装药量越小该现象越明显，在四号装药的挤进过程中出现了速度减小的情况。

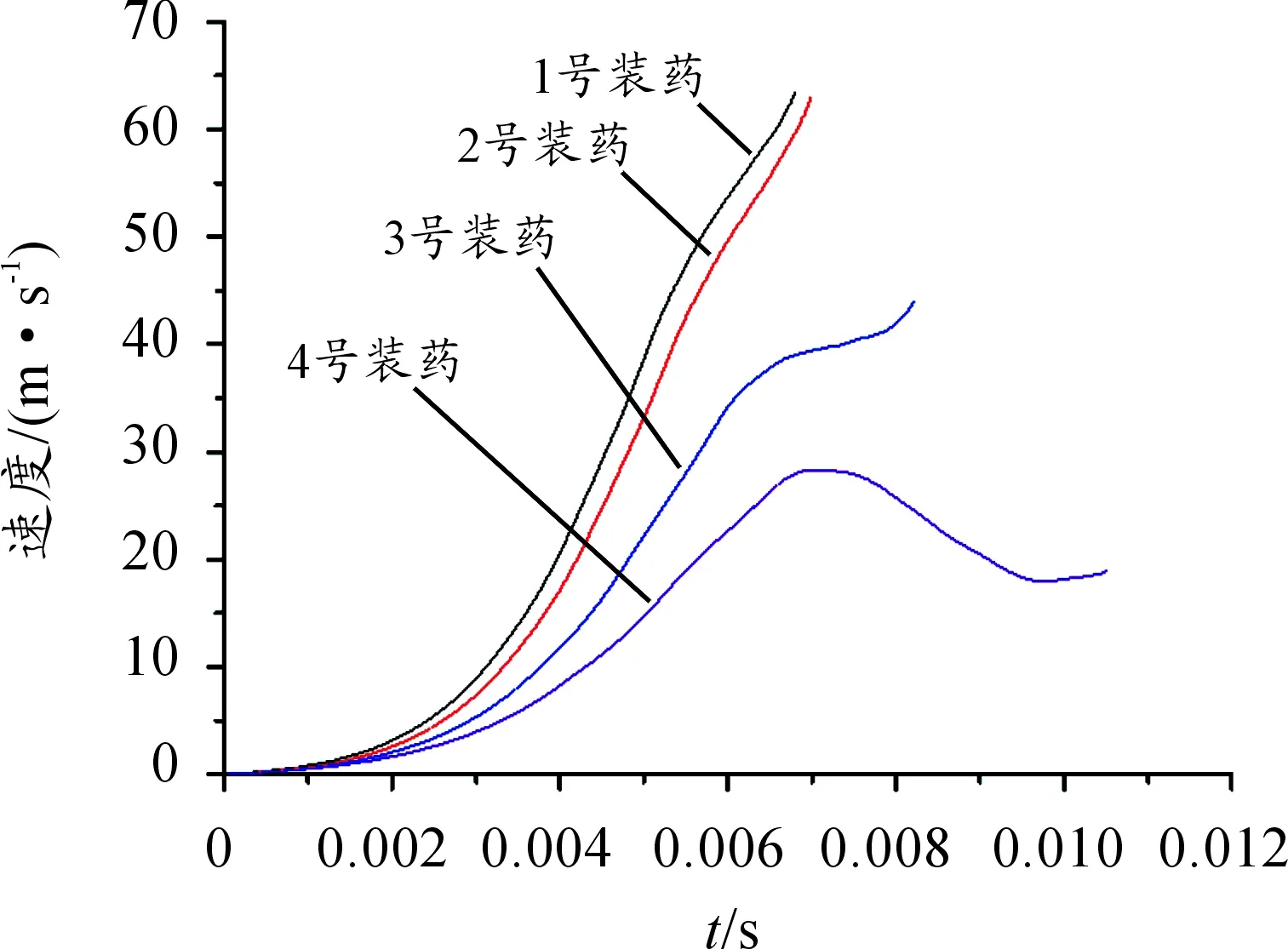
图5 弹带不同装药条件下速度时间曲线

对于这种现象结合图6加速度随时间变化曲线可以得出解释。由于该型火炮使用的是带凸台的双弹带结构，挤进开始之后弹带向前运动使得坡膛先和后弹带凸台接触，此时挤进阻力较小。随着膛压增加，弹丸的加速度迅速增加并继续向前运动，前弹带开始挤进膛线，挤进阻力逐渐增加；当弹丸运动直至膛线嵌入后弹带时，，挤进阻力迅速增大，膛压的增加速度低于挤进阻力的增加速度，导致加速度局部减小，当弹底压力低于挤进阻力时，加速度会出现负值现象。随着弹带的挤进过程的进行及弹底压力的上升，弹丸加速度再次增大，直至挤进过程结束。

从图7可以看出，在弹丸开始运动的10 mm行程内，挤进阻力为零，这是由于在模型的装配中为了防止过盈接触将坡膛和弹带间留有一定余量。；随着弹带接触坡膛开始挤进，弹带产生变形，挤进阻力开始缓慢增加，在25 mm行程内，不同装药状态下的挤进阻力保持为相同的值，约为71 kN；随着弹带的继续挤进，不同装药条件下的挤进阻力开始快速上升，装药量越大，挤进过程中的挤进阻力也越大。在弹带挤进55 mm时，挤进阻力上升速率突然增大，此时弹带挤进坡膛，弹带开始嵌入膛线，发生变形并且产生刻槽；挤进阻力随着弹带挤入膛线的部分的增加持续增大；当弹带挤进行程达到120 mm左右时，弹带主体完成挤进，阻力趋于稳定，在这一过程中，由于部分弹带材料的断裂失效，挤进阻力存在小幅度的震荡；当挤进行程到达140 mm时，弹带挤进完成，挤进阻力开始减小，直到弹带及其延伸部分全部挤进身管，挤进过程结束。

图6 弹带不同装药条件下加速度时间曲线

图7 弹带不同装药条件下挤进阻力行程曲线

同时由图7可以看出，弹带变形过程中挤进阻力最大值并不是在挤进结束时，而是出现在挤进过程结束前的某一位置，并且装药条件对该位置没有影响。此外，对比不同模块装药的弹带挤进阻力变化曲线可以得出，装药量越大，在相同位置处的阻力越大。这是由于随着膛内压力和上升速率的增大，在高应力和应变率条件下，弹带材料会出现应变硬化和应变率硬化，弹带的屈服应力和等效断裂应变随之增大，弹带的挤进阻力增加。弹带的挤进阻力受材料的塑性大变形和高应变率加载引起的热软化效应的影响。温度软化可以引起弹带材料的局部变形，减小弹带材料的等效断裂应变，抑制了挤进阻力的增加。火炮膛压和上升速率对于弹带挤进过程有很大的影响，因此不同模块装药对弹带的挤进速度、运动响应、动态挤进阻力和挤进压力产生很大的影响。

4 结论

1) 通过仿真得到了弹带的挤进规律以及不同模块装药对弹带挤进过程的动力学影响规律。不同装药量条件下弹带的挤进速度明显不同，装药量越大，燃气压力及上升速率越大，弹带挤进速度越快，完成挤进的时间越短。

2) 在装药量较小的工况中，火药燃气压力较小、上升速率较低，弹带挤进的过程中甚至出现负加速度现象。

3) 随着装药量增大，弹带相同位置处的挤进阻力随着装药量的增加而增大；不同装药量条件下弹带挤进阻力-行程曲线相似，存在缓慢上升和突然加速现象，在弹带断裂失效过程中，阻力呈现一定的震荡；在挤进过程结束前，阻力出现极大值，该值出现的位置取决于弹带与膛线的相对位置。

4) 弹带挤进阻力随着装药量的增加逐渐增加。在挤进过程结束前的位置阻力出现峰值，其出现位置与装药量无关。这一变化规律说明，为了精确刻画弹丸启动阶段的数学模型，提高内弹道仿真的精确度，有必要根据具体的弹带结构和装药条件总结出挤进阻力的动态变化规律。