多目标约束下装配线再平衡研究

张于贤，梁师文，杨梦珂

(桂林电子科技大学 商学院， 广西 桂林 541004)

装配线规划在现代复杂多变的大规模定制生产模式下扮演着重要的角色，装配线平衡与否直接影响制造系统的生产效率。

为了获得较高的装配线平衡率，须在工艺条件约束下，对全部装配工序按流水线节拍进行科学组合以使每个工位分配的负荷量充足且均衡。装配线平衡问题主要分为三类[1]，但在低成本，高效率且个性化的市场需求下，以装配线的工作站数为定值，求最小生产节拍的第II类装配线平衡问题仍是制造业目前须解决的难题。近年来，国内外学者针对第II类装配线平衡问题已经提出了诸多平衡数学模型及优化算法，其中文献[1-7]以最小生产节拍为目标函数构建单目标装配线数学模型，设计了各类算法对装配线问题进行求解，通过实例验证了算法的有效性和可行性。与单目标约束下的算法求解模型相比，尽管文献[8-10]设计了多目标装配线算法优化模型，可增强求解效果的可靠性和有效性，但仍有不少问题待解决：平衡约束模型未能更全面的反应实际生产现状，研究与实际应用依旧存在差距；智能算法虽然能够对工序作最优性排序，但仍存在最优解不符合装配线平衡最优准则的情形；多数文献从算法优化性能再改进入手提升求解效果，未能考虑到工序操作的复杂性和潜在的冗余性，且对瓶颈工序未能再深入地进行操作分析，使得装配线平衡率再提高。本文提出了基于GA-IE两阶段法的装配线多目标再平衡优化模型。

1 第II类装配线平衡问题描述

针对第II类装配线平衡问题，设工作站数目为K，工序集合为N，ti为工序i的操作时间；t(SK)为第k个工作站的工序时间，为了使得生产节拍最小化，须将所有工序均衡地分配到各个工作站。构建第II类装配线平衡模型须基于以下假设：

产品的装配工序时间已确定，工序逻辑优先关系已知；全部工序均被分配在工作站且只被分配到其中的一个工作站；工作站的数目是确定的；各个工作站由传送带链接，其传送速度一定，传送时间可忽略不计并且每隔固定的节拍时间投放一个待装配的零/部件。

为了解决单目标约束数学模型对装配线平衡界定比较单一化且模型结果与实际生产应用存在较大的偏差，提出多目标约束下的装配线平衡数学模型对装配线优劣作出较全面的评价，其模型可表示如下：

1) 最小化装配节拍：

(1)

2) 最小化平衡损失率：

(2)

3) 工作站间最小化平滑指数：

(3)

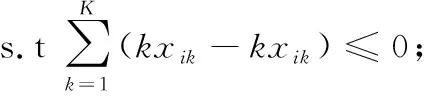
(4)

(5)

其中，式(1)表示以最大的装配任务时间为装配线节拍CT；式(2)表示最小装配线平衡损失率E*；式(3)表示平滑指数H，即分配到各个工作站上的装配任务时间总和与节拍的偏差，是衡量工作站负荷的指标；式(4)确保每项装配任务仅能被分配到其中的一个工作站，且决策变量xik属于0/1型，i=1,2,…,N；式(5)保证装配任务被分配时必须遵循工序优先级关系,PRE(j)表示按任务的先后顺序，i先于任务j完成的任务集合。

2 遗传算法设计

2.1 算法编码设计

采用二进制编码方式对装配线平衡问题进行编码，即通过二进制字符集{0,1}产生0/1字符串来表示问题空间的候选解。

译码过程是按照基因位次将工序分配到各个工作站，其操作步骤如下：

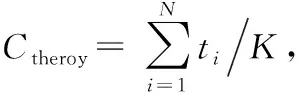
步骤2 以CT*为当前节拍，并将工序集合N按照基因位次分配到K个工作站中，K个工作站的时间分别为T1,T2,…,Tm,…,TK；ifTm≤CT*，则CT*为该排序下的最小节拍，即可停止搜索；否则，进行步骤3；

步骤3 计算各工序的潜在增量Δpr， Δpr(r=1,2,…,K)表示第k+1个工作站的第1个作业元素时间；

步骤4 令CT=max{Tm}，CT*=min{Tm+Δpr}，ifCT≤CT*，则CT*是该排序下的最小节拍，停止搜索；否则，进行步骤2。

本文研究的问题属于多目标函数情形，在求解最优方案须将多目标问题转化为单目标问题，通过考虑各目标函数式(1)、式(2)、式(3)将其设计成单目标评价函数f，定义如下：

fmin=α*CT+β*E*+γ*H

其中，α、β、γ为权重系数，且α+β+γ=1。

2.2 常规遗传算法操作

1) 初始化种群

利用随机法生成规模为Size的初始种群，其操作步骤如下：

步骤1 按照工序逻辑优先关系矩阵对工序作有序分配；

步骤2 将矩阵中已分配的工序对应的行和列均划去，更新优先约束矩阵；

步骤3 直至工序集合N中的所有元素均被分配完，则停止更新；否则重复步骤1和步骤2。

2) 选择

采用简单易操作的轮盘赌选择法。其基本思路：染色体被选中的概率与其适应度函数值成正比，其遗传到下一代群体的概率为

其中，F(p)为染色体p的适应度，轮盘旋转pop_size次。

3) 交叉

采用具有较强搜素能力的部分映射交叉算子[11](Partial-Mapped Crossover，简称 PMX)，其操作步骤如下：

步骤1 随机选择一对染色体(父代)中几个基因的起止位置，且被选位置相同；

步骤2 交换匹配基因；

步骤3 冲突检测。根据交换的两组基因建立一个映射关系，如图1所示，以1-5-6映射关系为例，能够发现步骤2结果中子代1存在两个基因1，则须将其通过映射关系转变为基因6，以此类推至没有冲突为止。全部冲突基因均须映射，保证生成的新一对子代基因无冲突。

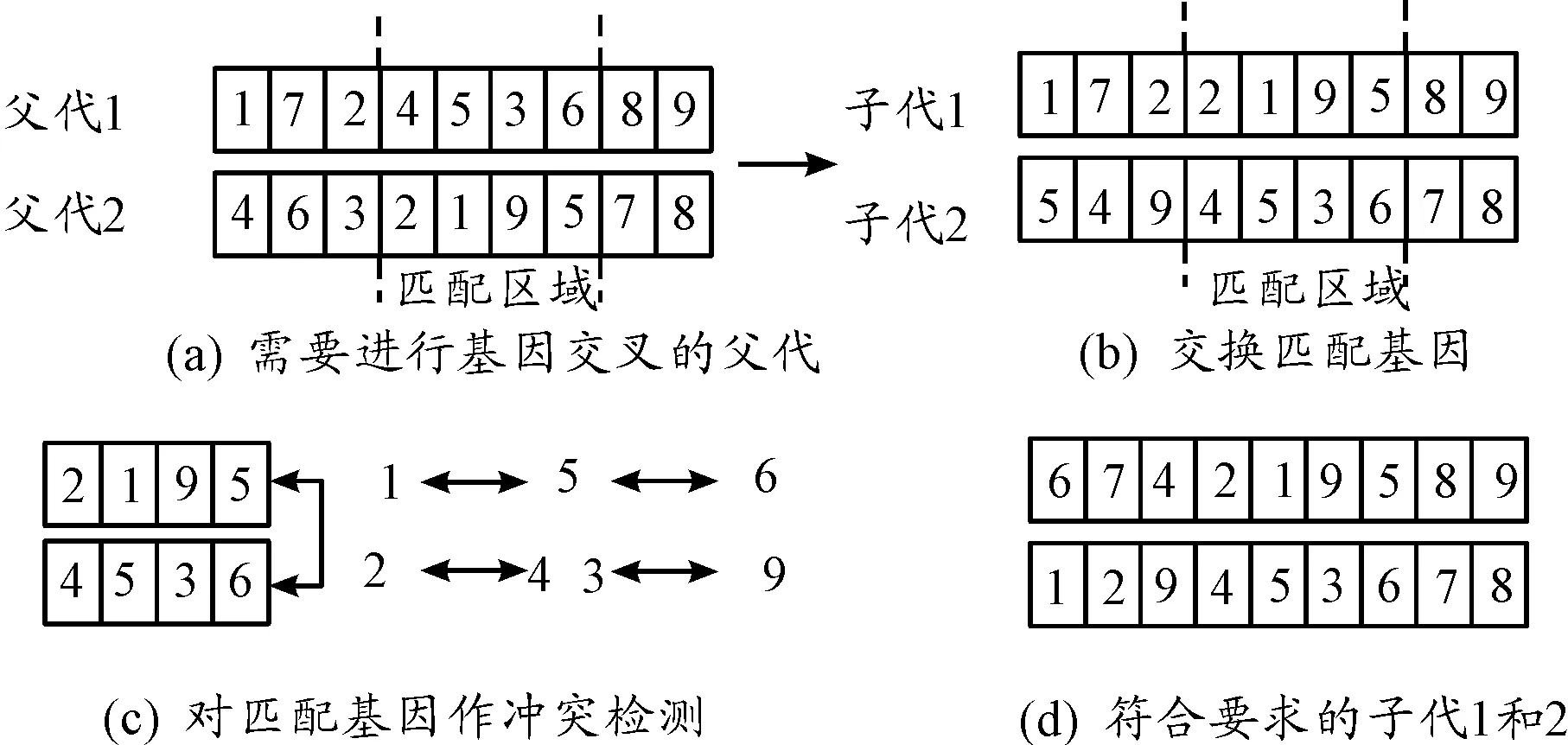
图1 PMX交叉操作

4) 变异

为了增加种群的多样性，采用交换-倒转-插入变异方式，其操作步骤如下(图2)：

步骤1 (交换)：随机选择1个染色体上的两个不同的基因，再交换它们在操作序列的位次；

步骤2 (倒转)：随机选择1个染色体上的4个不同基因，再倒转4个位置间序列的 顺序；

步骤3 (插入)：随机选择1个染色体上的1个基因，再将它随机插到操作序列的某个位置。

2.3 算法再改进切入点

为了解决常规遗传算法(Genetic Algorithm，简称GA)在求解种群规模较大时，存在过早收敛，且生成解容易陷入局部最优等问题，本文提出求解第II类装配线平衡问题的改进遗传算法，如图3所示，其中改进遗传算法采用两个层面，第一层面，利用遗传算法生成初始解，第二层面，嵌入具有“记忆”属性的禁忌搜索算法(Tabu Search,简称TS)对初始解进行寻优。

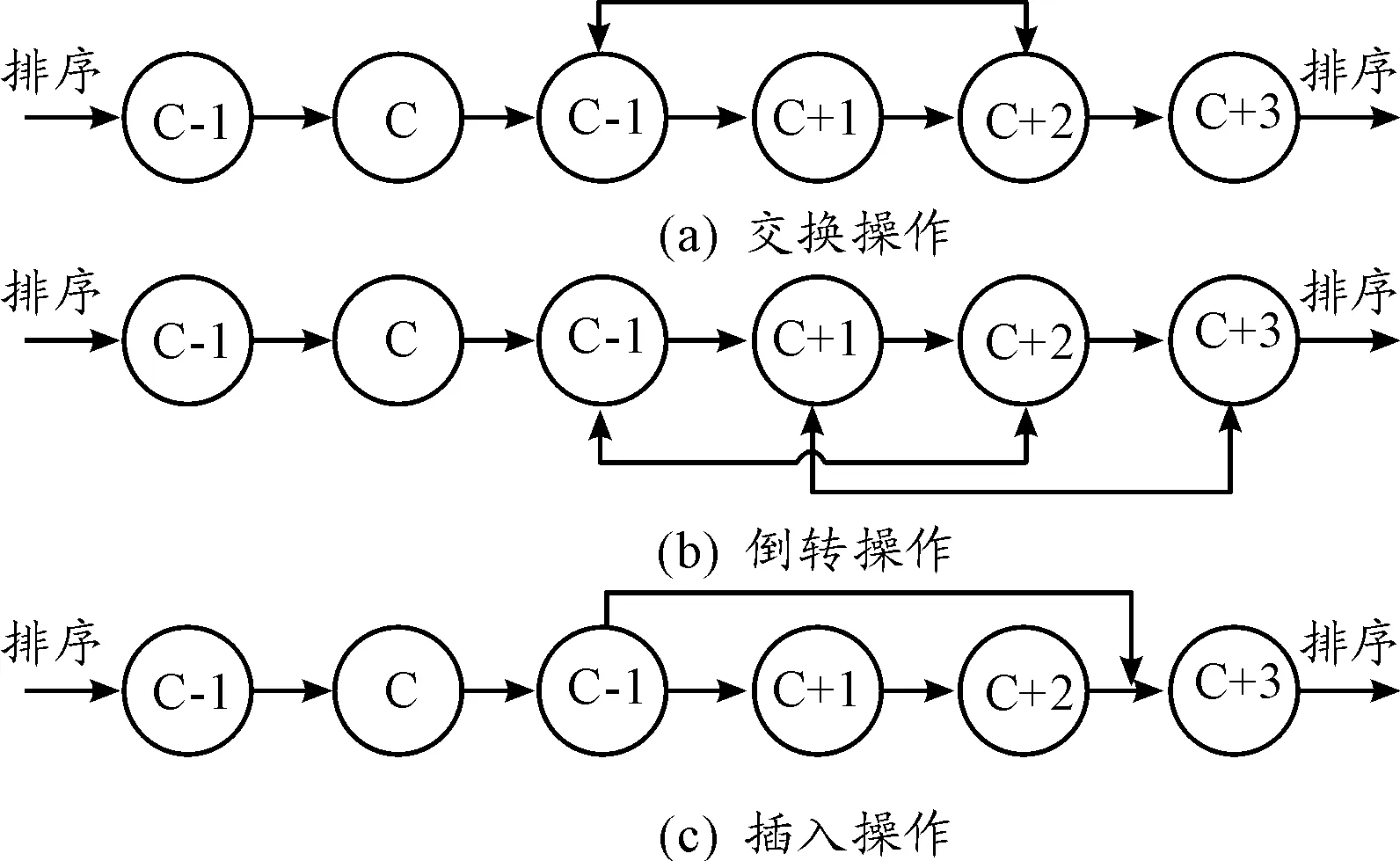
图2 变异操作

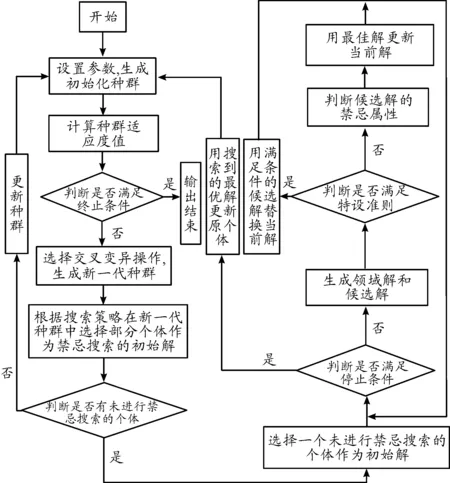
图3 改进遗传算法流程

3 实例验证

3.1 验证算法的准确性

经过测试，将遗传算法参数设置为：种群数Size=30,遗传代数MaxIt=300,交叉概率Pc=0.7,变异概率Pm=0.05,目标函数权重系数α=0.3，β=0.3，γ=0.4Z。而GA-TS算法在GA算法参数的基础上增加禁忌长TL=7,惩罚系数MPC=8即可，这样设置参数主要是控制参数一致性，有利于算法结果的可比性。

为了验证遗传算法和改进遗传算法(GA-TS)的准确性，在Matlab环境下，用经典的Jackson[12]和Buxey[13]平衡算例及某H产品装配线平衡问题(表1)进行验证，而分支定界法(B-and-B)求解平衡算例的结果作为GA算法和GA-TS算法运行结果的对比对象，算法运行结果如表2所示。

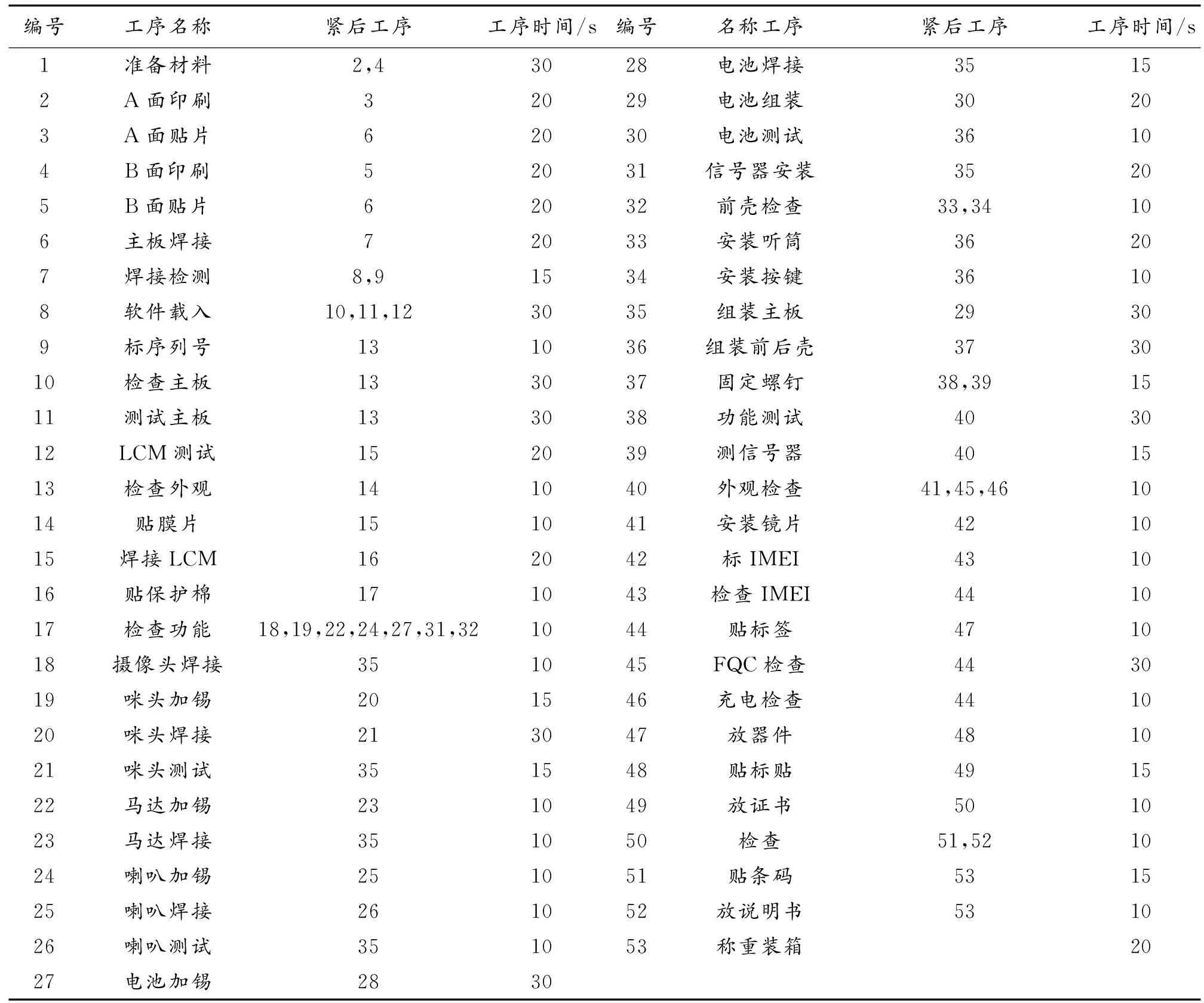
表1 H产品装配工序顺序

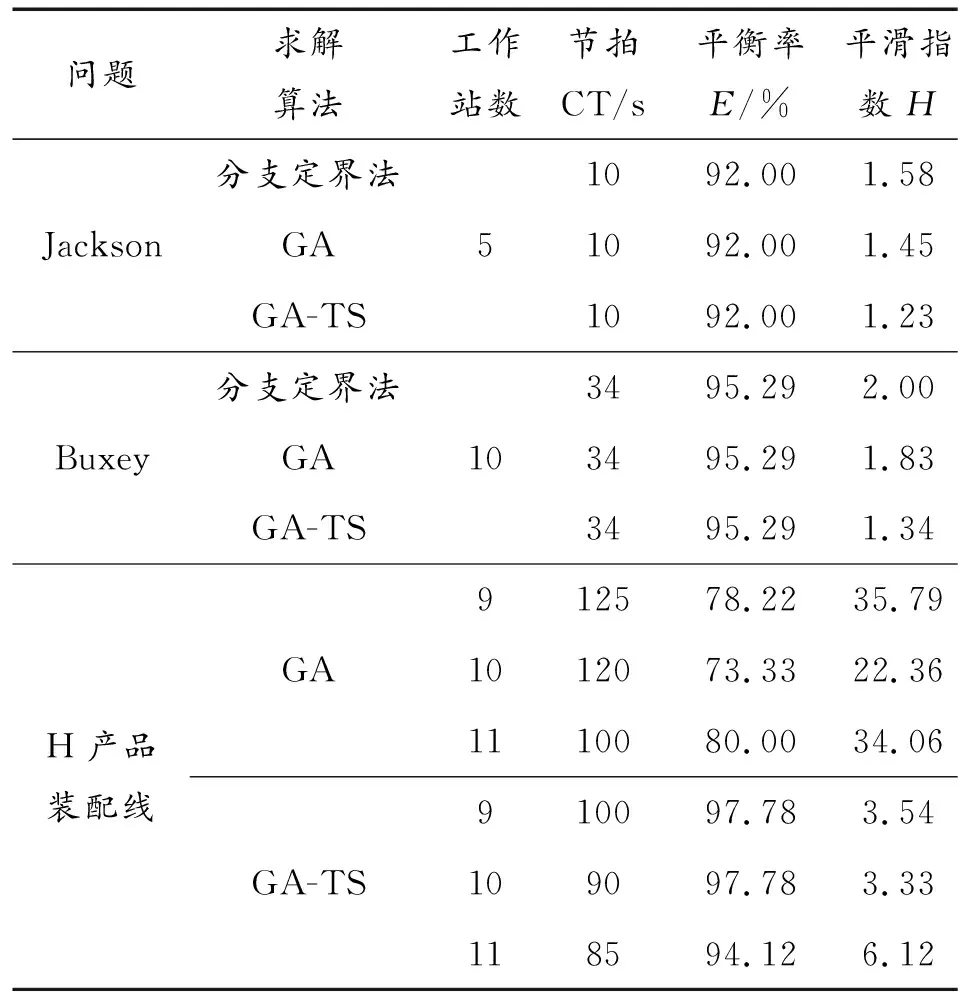
表2 算法对测试问题的运行结果

经表2结果可看出，GA-TS算法、GA算法与分支定界法(B-and-B)在工作站数K相同的情形下求解Jackson和Buxey问题，GA-TS算法求解效果较好于GA算法和B-and-B算法得到最优解，表明GA-TS算法、GA算法的求解结果均准确。

在不同工作站数K的情形下分别采用GA-TS算法和GA算法对H产品装配线平衡问题进行优化求解。当工作站数取值相同时，GA-TS算法优化求解的节拍CT、平滑指数H均低于GA算法的结果，且平衡率E*较好于GA算法得到的解，表明GA-TS算法得到的解更优，效果更佳。

在实际生产中，给定的H产品工作站数K=10，GA算法获得最优解对应的工位图，如图4所示，其中图4中的[(39，15)，station1]表示编号为39且时间为15 s的工序被分配到工作站1。GA算法得到的最优解节拍CT=120，平滑指数H=22.36，生产线平衡率E*=73.33%未达到装配线平衡最优准则要求，即生产线平衡率只有在85%以上时，生产系统是按照“一件流”的生产模式[14]运行。

为了满足生产要求，在GA算法最优解的基础上，提出利用IE技术对H产品装配线再改善思想，则构成两阶段体系模型，其中第1阶段，利用GA算法对装配线平衡问题进行优化求解，第2阶段，应用IE技术针对第1阶段算法求解的不符合要求的最优工位作瓶颈分析，并进行持续性改善，得到满意的再平衡方案，如图5所示。

图4 GA算法最优解对应的工位图

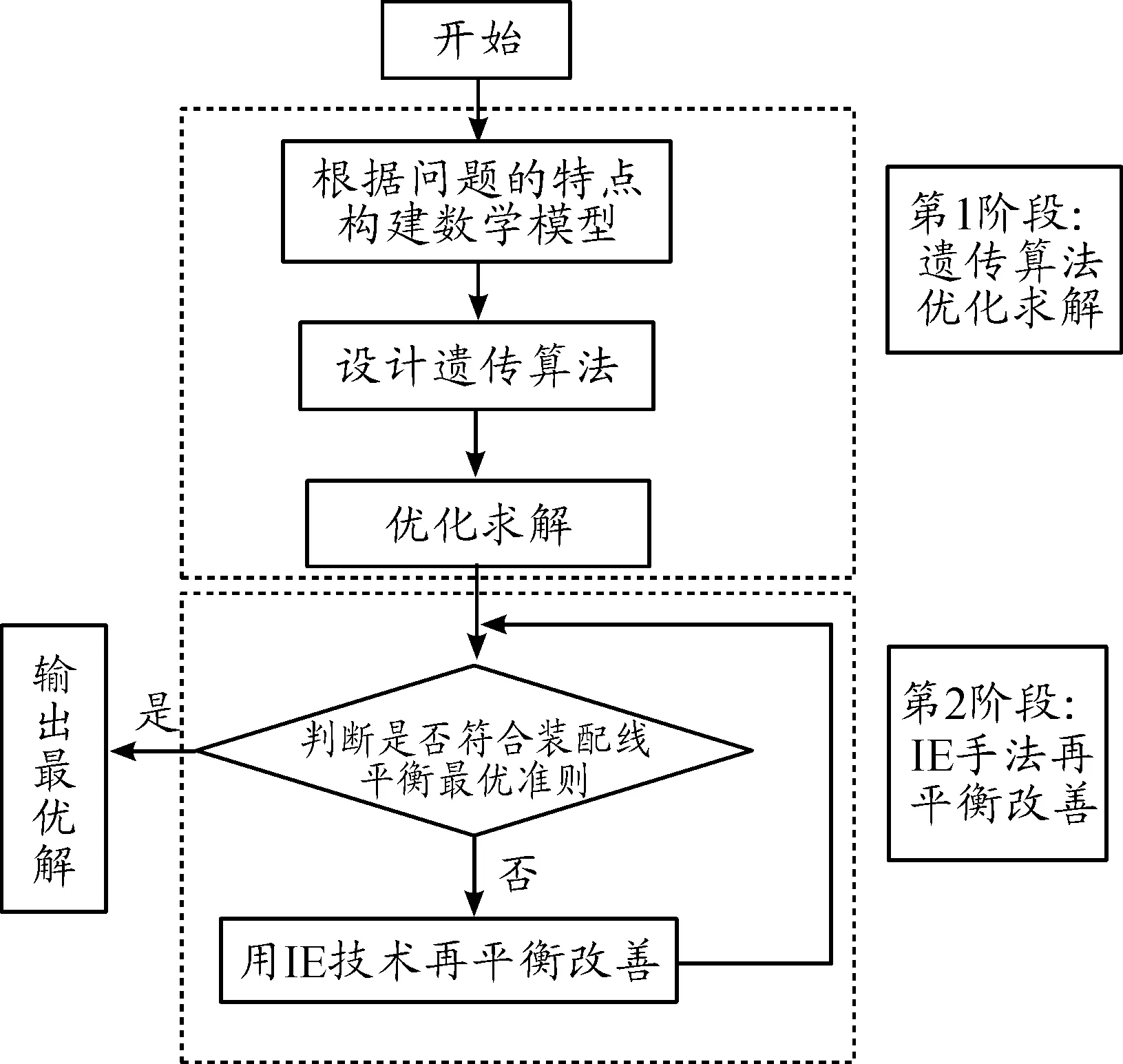
图5 两阶段体系模型

3.2 IE技术再平衡改善

由图4可知，第1、3、4、10工位的加工时间比较长，处于忙碌状态，是整个流程的瓶颈环节，也是造成后续工位高空闲率的因素。因为工作站负荷不均衡，限制了装配线的整体产出效率，对其余工位的生产能力产生了瓶颈效应，因此，利用工业工程(Industrial Engineering,简称IE)技术[15]对第1、3、4、10工位的工序进行重点再改善。

以第10工位中的6号工序为例进行双手作业分析，对多余及无效的动作进行改善，其改善前的双手作业分析结果，如图6所示。

通过对H装配线不合理现象的分析，利用“6W1H”提问技术和“ECRS”原则对6号工序进行双手作业改善，其中提问技术从生产作业的七个方面(作业要完成什么(what)、在何地做(where)、何时做(when)、何人做(who)、为谁做(for whom)、作业方法(how)和为何这样做(why))有序的探寻问题的根源，能够快速准确地对生产作业现存的问题作出定位，并发现问题产生的原因。再通过“ECRS”原则对提问技术找到的作业问题进行取消(Eliminate)、合并(Combine)、重排(Rearrange)、简化(Simplify)5个环节的调整，使得6号工序时间由20s 降低到14 s，其结果如图7所示。

依据6号工序的改善思路对第10工位的其余工序及第1、3、4工位进行改善，其结果如表3所示。

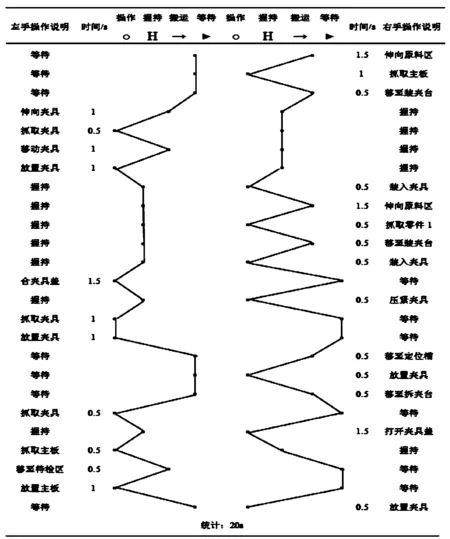
图6 改善前主板焊接双手作业分析

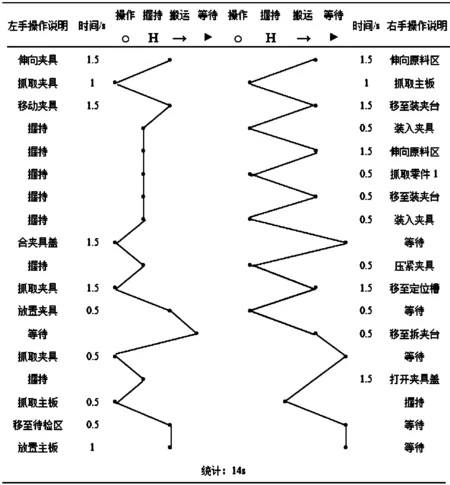
图7 改善后主板焊接双手作业

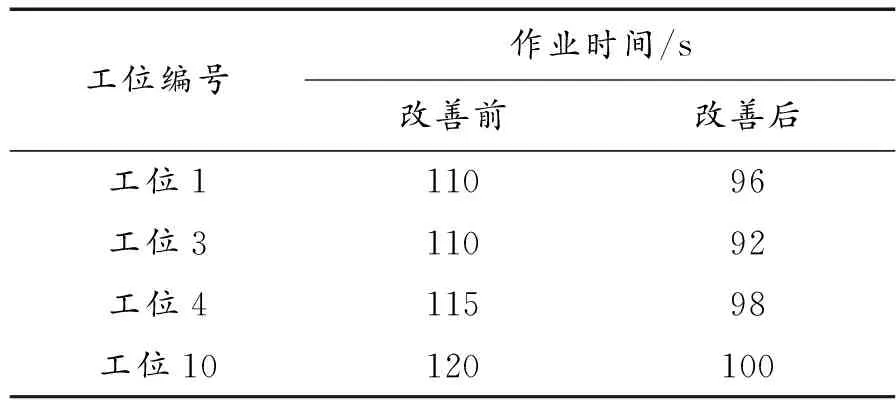
工位编号作业时间/s改善前改善后工位111096工位311092工位411598工位10120100

经过对瓶颈工序进行改善，瓶颈节拍CT由原来的120 s变为100 s，平滑指数H由22.36变为18.65，平衡率E*由73.33%变为88.00%，符合“一件流”的生产模式要求。

3.3 验证两阶段法求解程度

为了证实两阶段法的求解效果是非最优解一猜想，提出直接利用改进遗传算法对H产品装配线平衡问题寻优求解。在工作站数K=10时，瓶颈节拍CT=90 s，平滑指数H=3.33，平衡率E*=97.78%，其最优解对应的工位图，如图8所示。将两阶段法和改进遗传算法求解结果对比，结果表明：两阶段法得到的结果是非最满意解，但是一个有效可行解；改进遗传算法寻优效果较好，但未能从作业操作改善的角度提升生产线效率。

图8 改进遗传算法最优解对应的工位图

4 结论

本文通过构建以装配线平衡损失率、装配节拍和站间平滑指数为最小优化目标的第Ⅱ类装配线平衡模型，通过实例验证了GA算法和改进GA算法的准确性。根据实际问题的特点，利用GA算法优化H产品装配线，其最优解未能符合“一件流”的生产模式要求，提出了IE技术与GA算法相结合的再平衡改善策略，使得装配线效率从73.33%提升到了88%，且将GA-IE两阶段法和改进GA算法的求解结果作对比，结果表明：GA-IE两阶段法求解效果符合生产活动要求，但获得的是可行解，非最优解。两阶段法可以为生产管理人员在装配线规划方面提供方法支持。