节片式柔性导引设计与仿真

罗 露，戴劲松，樊永锋，王茂森

(1.南京理工大学 机械工程学院， 南京 210094； 2.中船重工七一三研究所， 郑州 450000)

供弹传输技术是支撑火炮持续高速作战的关键技术。无链供弹传输系统没有除链排链过程，能够突破传统有链供弹限制自动机射速的瓶颈[1]。廖瑞珍对某供输弹系统螺旋导引进行设计，研究了弹链供弹的运动规律[2]。郑建兴设计出了一种节片式柔性导引能够过渡自动炮在高低俯仰变化时与刚性导引之间产生的扭转[3]。本研究提出了一种适用于无链供弹的新型节片式柔性导引结构，既充分利用弹链可以相互扭转的柔性特性又利用节片之间可变形的特点，设计出节片式柔性导引机构能够分别直线传输弹丸、扇形传输弹丸以及扭转传输弹丸，使弹箱与自动炮之间布置具有更大的灵活性，从而充分利用有限空间，获取更大的弹药基数，提高作战单元的战斗力和生存能力。

1 柔性导引设计

1.1 柔性导引几何特征

该柔性导引由若干节片组成，节片连接示意图如图1所示。节片上安装有若干簧片，后一节片上的簧片搭接在前一节片内，节片中心安装有带有球头链节的连接杆，之间通过鼓形销轴连接来实现节片之间的相对扭转，鼓形销轴的直径要小于球头链节上孔的直径，以此来保证两节片之间的扭转自由度。

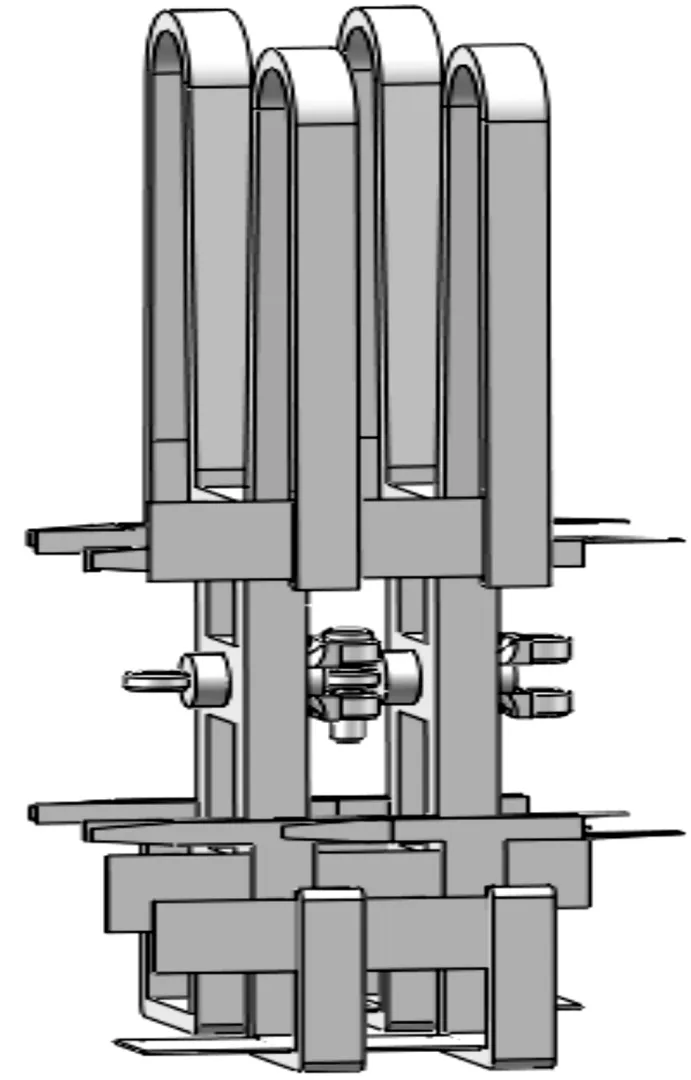
图1 节片连接示意图

弹夹安装在导引内，通过由簧片形成的通道限制其运动轨迹。弹丸则通过安装在节片上的不锈钢片规整其运动轨迹。弹夹与弹夹之间通过鼓形销与球头链节的方式连接。弹夹链节与弹夹链节之间的相对扭转角度可达15°，理论上7个弹夹链节就可实现90°的扭转量，但实际当中相对扭转角度不宜过大。根据实际工程经验，弹夹与弹夹之间的扭转角度要小于等于5°，其弹链柔度示意图如图2。

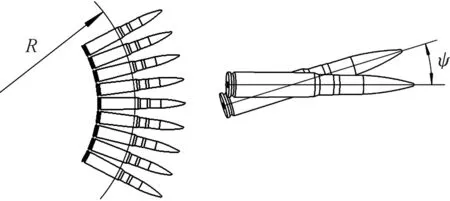
图2 弹链柔度示意图

1.2 柔性导引节片设计

过弹截面可以根据弹链长度、直径和链节节距确定，节片大致轮廓如图3所示。

图3 节片轮廓

为了确定两节片之间的位置关系，取卡尔丹角系，(α，β，δ)分别为铰球板先绕固联其上的坐标系X轴旋转α，再绕Y轴旋转β，最后绕Z轴旋转δ。都按右手法则，取逆时针为正。取节片Dj相对于节片Dj-1平移为Dsj(0，0，dzj)，dzj为变形前两节片距离，则j节片相对于j- 1节片的关系，有：

(1)

Krj=Mj(K+Dsj)

(2)

则j节片在OXYZ坐标系中的表示有：

(3)

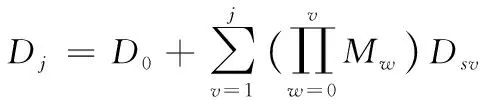
(4)

(5)

弹丸要从进弹口输送到出弹口，要实现侧弯传输、扭转传输和直线传输三个过程，在Mathcad软件中可以建立节片的空间位置模型，如图4所示。

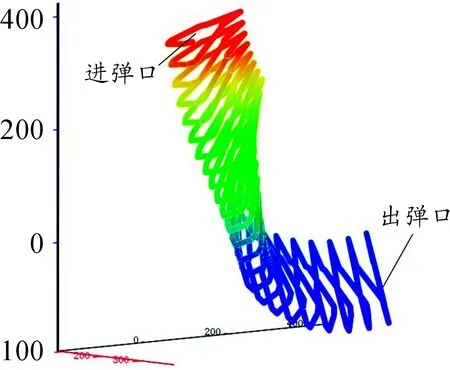
图4 节片空间模型

由于确保弹夹通过的通道是由若干伸出节片的不锈钢簧片组成，在设计时，必须保证在各种变形条件下簧片的强度满足使用要求，运用弹性理论可以计算出37 mm长不锈钢簧片的最大变形，如表1所示。

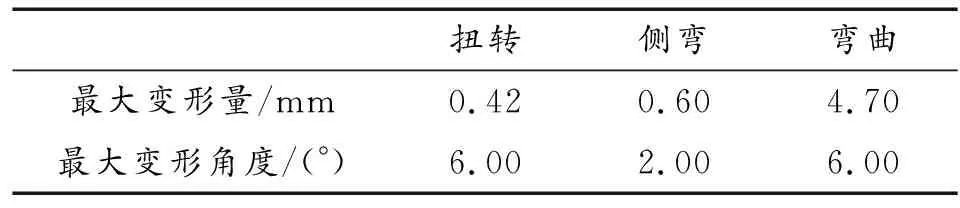
表1 节片在各变形条件下的最大变形量

由前文所述，可以设计出节片式柔性导引机构如图5所示，该节片式柔性导引机构由中间的柔性节片、两侧刚性导引、弹夹与弹丸形成的弹链和拨弹轮组成，弹丸和弹夹安装在节片和两侧刚性导引所形成的通道内，拨单轮波动弹丸带动整个弹链运动。

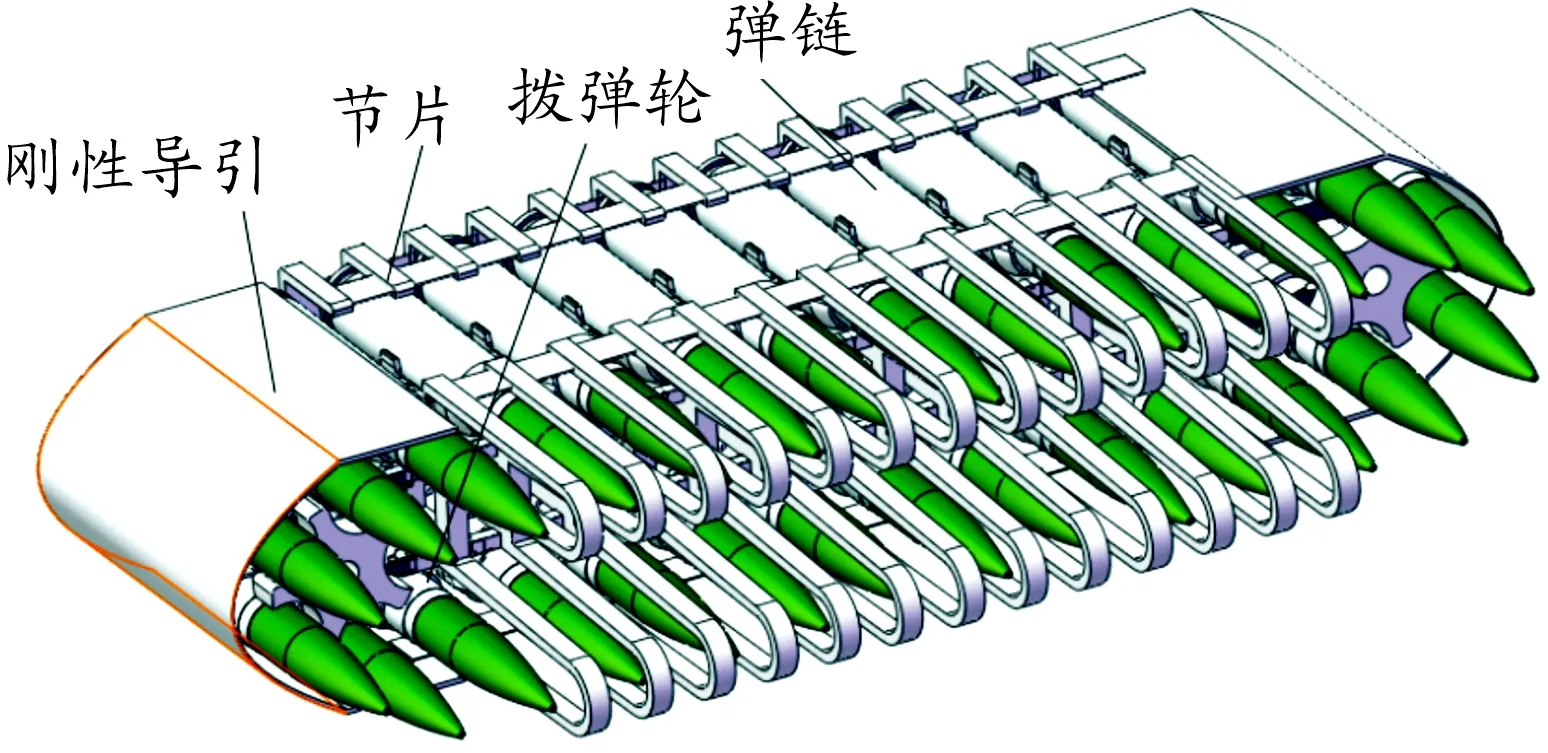
图5 节片式柔性导引示意图

2 节片式柔性导引机构虚拟样机模型

ADAMS中主要利用第一类拉格朗日方程来建立基于约束的机械系统运动学和动力学方程。机械系统坐标常采用笛卡尔坐标系，即利用构件中某质点的三个直角坐标和欧拉角为广义坐标，通过对带有拉格朗日乘子系统约束进行处理，导出以三个直角坐标和欧拉角为广义坐标变量的动力学方程。对刚体质心位移的描述，采用其质心在惯性参考系中的笛卡尔坐标和反映弹丸刚体方位的欧拉角作为广义坐标来表示，即：

q=[x,y,z,ψ,θ,φ]T

(6)

式中：质心坐标(x，y，z);欧拉角(ψ，θ，φ)。

考虑约束方程后，利用带拉格朗日乘子的拉格朗日第一类方程的能量形式方程：

(7)

将集成约束方程自动建立系统的动力学方程，即微分代数方程：

(8)

式中：T为系统广义坐标表达的动能；q为广义坐标；Q为广义坐标在q方向上的广义力；Φ为系统约束方程；P为系统广义动量；H为外力的坐标转换矩阵。

根据所建立的节片式柔性导引机构的三维模型，对虚拟样机模型进行简化，简化的原则是既能顺利的仿真验证弹丸在柔性节片导引中运动的通畅性，又能比较真实地反映弹丸在柔性节片导引内的运动规律。对节片式柔性导引机构作如下简化：① 由于节片式柔性导引的空间模型由较多节片通过不同变形完成，零件繁多，约束复杂，计算很繁琐，研究中将取部分节片分别模拟弹丸在节片式柔性导引中的运动情况，分别为扭转传输、侧弯传输和直线传输。② 间隙、弹性变形是鼓形销的主要特征，因此，弹与弹之间采用等效集中质量弹簧阻尼模型[5]，将鼓形销简化为球铰与弹簧的连接方式。虚拟样机模型如图6所示。

将三维模型导入ADAMS后，需要根据实际情况对各零件施加约束，在具有相互运动的两构件之间添加约束副和碰撞接触，主要约束关系如表2所示，根据Hertz弹性接触理论，本研究中碰撞力参数选取：刚度系数均为1×105N/m，最大穿透深度均为0.1 mm，力指数均为2.2。

3 仿真结果分析

仿真中直接给拨弹轮的圆柱副添加180 r/min的恒定转速研究弹丸在柔性导引各情况下的运动情况。

第一段柔性导引在扭转情况下弹丸运动情况如图7、图8所示。

图6 节片式柔性导引虚拟样机模型

约束副类型部件1部件2固定左侧拨弹轮/左侧导引大地固定右侧拨弹轮/右侧导引节片8圆柱副连接杆连接杆弹簧弹夹连接杆碰撞弹夹/弹丸节片/左侧导引/右侧导引碰撞弹丸拨弹轮

图7 弹丸质心位移曲线

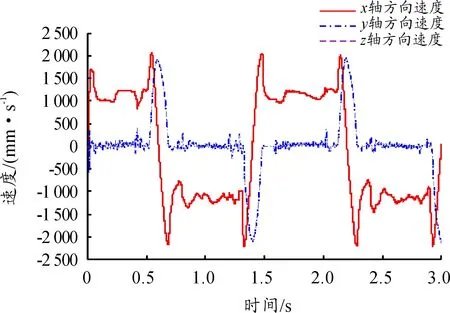
图8 弹丸质心速度曲线

第二段柔性导引在侧弯情况下弹丸运动情况如图9、图10所示。

第三段柔性导引在直线情况下弹丸运动情况如图11、图12所示。

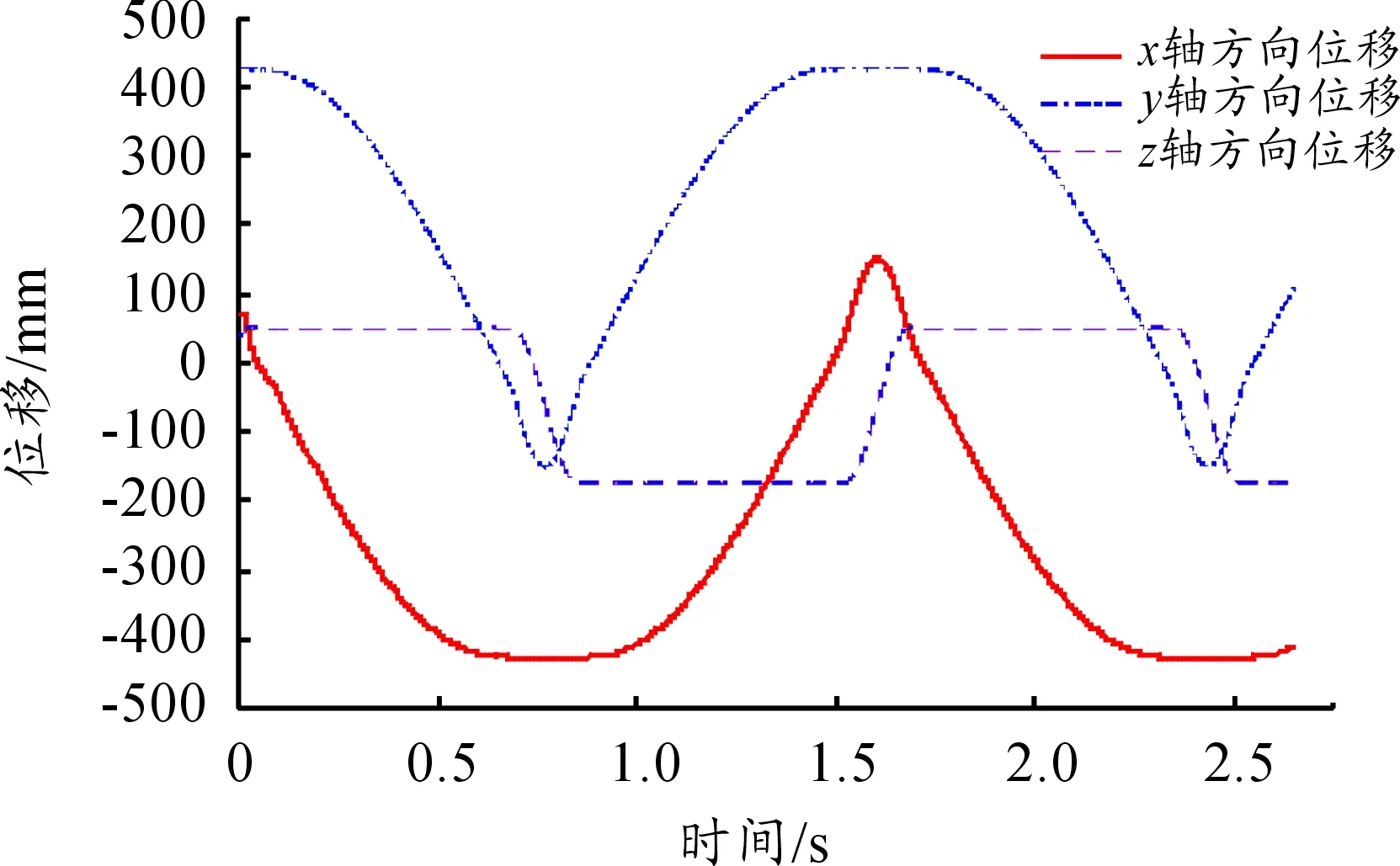
图9 弹丸质心位移曲线

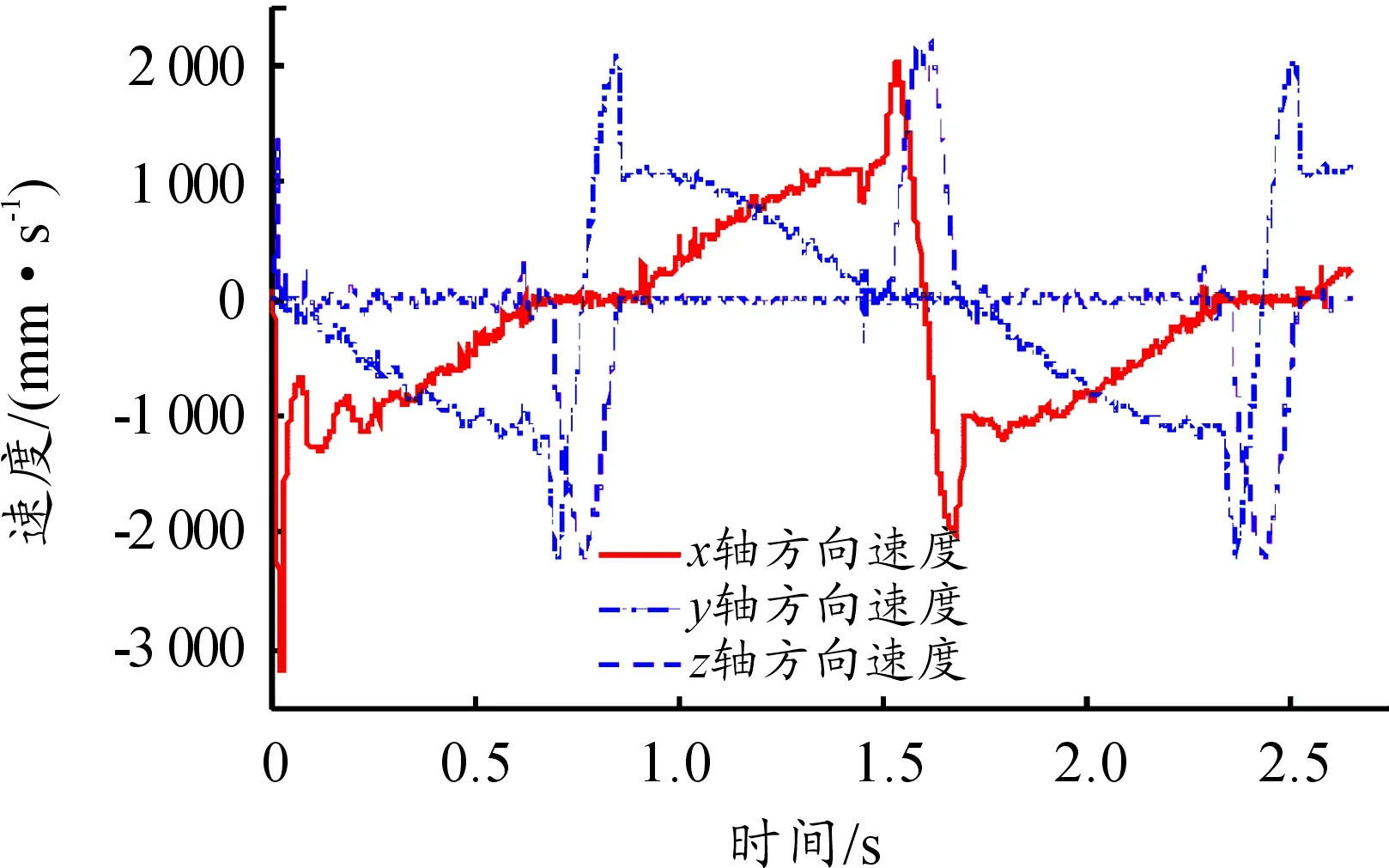
图10 弹丸质心速度曲线

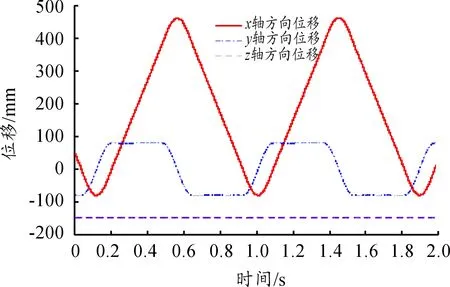
图11 弹丸质心位移曲线

图12 弹丸质心速度曲线

由图7～图12可以看出，三种情况下，弹丸的位移曲线光滑，没有出现突变，证明该柔性导引机构能够顺利完成弹丸的传输。在拨弹轮的拨动下，整个闭合弹链开始运动，弹丸经过刚性导引进入由若干节片形成的柔性导引内，在里面传输一段时间后出柔性导引继续在刚性导引上传输，然后经过拨弹轮继续反向传输。由三种情况下速度曲线可以看出，当弹丸经过扭转部分时，弹丸在x轴方向的速度(拨弹轮赋予弹链的主要速度)迅速增加至一个峰值后减小至一定速度后平稳，再增大到一个峰值后减小至零后反向重复之前的运动，此间速度存在一定波动，波动出现在经过两侧拨弹轮处，最大速度达到2 053 mm/s；当弹丸经过侧弯部分时，弹丸在x轴方向上的速度由最大值慢慢变为零，y轴方向速度由零变为最大值，表明弹链运动方向由x轴方向转为y轴方向，弹丸经过拨弹轮时产生z轴方向的速度，在这过程中x轴和y轴方向速度在拨弹轮处产生一定波动，最大速度为3 105 mm/s；当弹丸经过直线部分时，弹丸在柔性导引内速度(x方向速度)波动较小，仅在接触拨弹轮时有轻微的速度波动，最大速度为1 362 mm/s。综上所述，三种情况下弹丸的速度曲线在柔性导引内较平滑，能够保持平稳传输，仅在拨弹轮处出现尖峰，引起传动速度的波动主要是由于链传动的多边形效应和弹丸与刚性导引之间的间隙产生，可以考虑优化拨弹轮齿形和设置合理的间隙来减小弹丸速度的波动。

4 结论

对节片式柔性导引进行了结构设计和仿真。仿真结果证明节片式柔性导引的结构简单可行，可以实现在一定条件下连续和确定的供弹，由于间隙的影响，弹丸速度存在一定振荡，使得弹丸在传送过程中会有一定的速度跳动和冲击碰撞。弹丸位移曲线相对平稳，弹丸在软输弹导引三种情况下都能够顺利通过，证明了方案可行，可为节片式软输弹导引的设计提供了参考。