在“磨课”中升华——以“幂函数”为例

辽宁省大连市第八高级中学 鲍 焕

老师们常说：“好课是磨出来的，好教师也是磨出来的。”而对于青年教师来说，“磨课”更是提升课堂教学能力的必经之路。青年教师应多上公开课，在磨课过程中成长、升华。本文笔者作为青年教师以自己的一次赛课经历为例，谈一下磨课的感受，在整个过程中，可谓既有“山重水复疑无路”的迷茫，又有“柳暗花明又一村”的惊喜。

一、磨课准备

1.确定选题

《普通高中数学课程标准（2017 年版）》指出：“幂函数是最基本的、应用最广泛的函数，是进一步学习函数的基础。”本节内容在整个高中数学体系中起到了承上启下的作用：一是本节课之前已经学习了指数函数和对数函数，是对关系式N=ab的又一个方向的探究，并且在初中阶段学生已经学习了部分具体的简单幂函数，只是没有引入幂函数的概念，本节课在此基础上对幂函数的一般性质进行了探究；二是本节课研究幂函数的方法是从已经学过的具体幂函数入手，抽象出幂函数的一般性质，再将这些性质应用到具体的幂函数中的过程，为后续学习方法起到了引领作用。本节课不仅仅是知识的学习，更是对学生思维的引领，这就要求教师要有一定的高度，对教师的技术素质和能力素质都是一次考验。

2.了解学情

在磨课之前，笔者通过布置预习作业和谈话的方法对学生的情况进行了解。在初中阶段，学生已经学习了反比例函数、一次函数、二次函数，已经掌握了这些函数的概念和图像，再结合高中所学的函数的单调性和奇偶性，对这些函数的性质有了更进一步的研究；学生对作图方法只知道用描点法作图，不会从函数性质的角度分析函数的图像；在高中阶段还学习了指数函数和对数函数，对幂函数的学习起到了铺垫作用。但部分学生对已学过的内容掌握不够扎实，对知识的理解只停留在表面。结合课标和教材，针对学情确立教学目标、重难点以及问题的难度。

3.进行教学设计

教材和课标是把握好一堂课的重要素材，尤其是此次课程改革后的新教材和新课标，教师在上课之前必须细心研读。笔者结合课程标准对教材中的内容进行了梳理和重组，并与组内同事进行了研讨，作出了本节课的教学设计。

4.设计导学案

根据教学设计的内容设计本节课的导学案，分别包括“课前案”“课中案”和“课后案”三个部分。力求版面设计能够激发学生学习兴趣，内容设计能够引导学生高效学习，问题设计能够符合学生的最近发展区。

5.制定课件

根据教学设计形成一堂课的教学思路，在此基础上制作好本节课的教学课件。结合学科特点，课件以PPT 为主，几何画板为辅，让图像更加直观，以激发学生的学习兴趣，提升课堂效率。

二、磨课实践

教学过程分为课题导入、自主学习、合作展示、反馈拓展、课堂小结五个环节。本节课教学设计经历了两次试讲，两次教学设计的修改，在此不一一赘述每个环节反复推敲的过程，就以合作展示环节为例来进行说明。

（一）第一次教学设计

合作展示。

活动1：在同一直角坐标系中作出下列幂函数的图像。

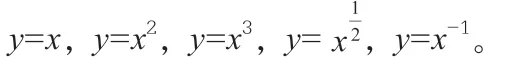
活动2：结合函数的图像和表达式，你能给出活动1 中各个函数的定义域、值域、奇偶性、单调性以及它们的公共点吗？

问题3：根据上述表格，你能归纳幂函数的性质吗？

设计意图：通过小组合作展示，探究幂函数的性质，培养学生的归纳概括能力、语言表达能力和团队协作能力。

同事评价与自我反思。

试讲过后是笔者的说课过程，紧接着就是数学组全体教师评课磨课的过程。原本自认为是理想的课程设计，可是在实际课堂教学中并没有达到理想的效果。

在评课中，大家主要的观点集中在以下几个方面：（1）本节课教学环节看似完美，但学生的参与度不高，合作展示环节问题设置太过局限，限制了学生的思维；（2）本节课的重点之一应是画幂函数的图像，重点不够突出；（3）本节课应该引领学生研究一个未知函数的方法，而并不只是幂函数，这样的教学设计可能导致学生只注重局部，不能从整体意义上思考问题。

评课之后，笔者对本节课进行了自我反思：（1）从形式上看，本节课教师以问题的性质引导学生思考，但学生的主体地位体现不够，教师应设置具有真正启发意义的问题来进行有效的提问；（2）本节课对学生核心素养的落实重点在几何直观和数学抽象，结合新课标，这样的教学设计只完成了数学核心素养水平一，并且对学生思维的提升和方法的引领不到位，缺少高度。 结合同事的评课，笔者仔细研读新课标，查阅资料，对教材进行了重新梳理，对教学设计进行了修改。

（二）合作展示环节的第二次设计

问题1：函数的性质有哪些？

活动1：在同一直角坐标系中作出下列幂函数的图像。

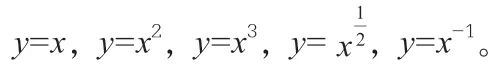
问题2：结合上述函数的图像和表达式，你能得到幂函数的哪些性质？

教学活动的重新设计后又进行了试讲，此次问题的设计更加开放，学生的思维参与度有所提升，收到了较好的效果。课后再次进行了反思，应该让学生通过本节课获得研究问题的一般性思维方法，以达到数学核心素养的水平三，于是对教学设计进行了再次修改。

（三）合作展示环节的第三次设计

问题1：我们研究哪些幂函数的性质？即α 取何值时更具有代表性？

问题2：我们将如何研究这些函数的性质呢?研究函数性质的方法有哪些？

问题3：函数的性质包括哪些？

问题5：思考研究函数的性质用什么方法呢？

设计意图：通过小组合作交流，明确哪些是具有代表性的幂函数，并引导学生研究函数性质的方法有两种，一种是通过函数图像，一种是通过函数表达式，数形结合。同时获得研究函数的一般方法，即从具有代表性的函数入手，总结出一般性质、规律，再将一般性质、规律应用到具体的问题中，这也是人们认识事物的一般过程：从特殊到一般，再从一般到特殊，这对学生今后的学习和生活具有重要的指导意义。

三、磨课反思

1.磨课“磨”出专业知识新高度

传统观念对教师的知识储备需求是“要给学生一杯水，教师须有一桶水”，但对于知识不断更新的现在，这种说法早已过时，而是主张“要给学生一杯水，教师必须有源源不断的活水”，而磨课便是这源源不断的活水的来源之一。在磨课中不仅会对教材和新课标有更加深刻的理解，而且磨课可以说是整个数学组的一次教研，同事间的思维碰撞，无疑是一个更新知识、提升自我的过程，在磨课过程中也要搜集资料、阅读书籍，这也为教师知识水平的提升有所助益。总而言之，所谓“磨”，既包括本学科知识，也包括相关学科的知识，当然也少不了教育理论知识，教师的专业知识就是在这种“磨”的过程中得以巩固。

2.磨课“磨”出专业技能新高度

专业化的教师必须具备从事教育教学工作的基本技能和能力。而每次的公开课都是对教师专业技能的一种考量，除了粉笔字、板书设计、普通话等教学基本功外，教师在讲课过程中的一言一行，一举一动，通过与学生互动表现出的亲和力、幽默感以及处理应急问题的能力等综合素质，都是评价一节课成功与否的标尺，而磨课便是一种提升教师专业技能的最佳实践途径。

3.磨课“磨”出教学情谊新高度

经历了磨课的艰辛过程之后，专业技能、专业知识等方面都得以提升，便会有“化茧成蝶”般的喜悦和满足，会更加热爱教育事业。磨课之前的抵触心理完全消失，取而代之的是在磨课过程中的坚持，形成了奋斗不息、追求不止的精神。苏霍姆林斯基也曾说“要用一辈子的时间准备一节课”，在今后的教学过程中，我会发自内心地愿意去再次经历这种“磨”的过程。