三组分气体超声速凝结过程数值模拟与实验研究

曹学文， 边 江， 靳学堂， 尹鹏博， 杨 文(.中国石油大学(华东) 储运与建筑工程学院， 山东 青岛 66580； .合肥燃气集团有限公司， 安徽 合肥 30075)

井场开采出的天然气主要成分为甲烷，同时还含有一定量的水分、重烃、酸性气体等，这些组分会对天然气输送造成严重的危害。水和重烃的凝结会增加管道流动阻力，增加输送能耗，同时还有生成水合物堵塞管道的风险；硫化氢和二氧化碳等酸性气体溶解于液态水中会对管道造成腐蚀，缩短管道寿命。为保证天然气的安全储存与输送，需对天然气中水、重烃、酸性气体等组分进行分离处理[1]。超声速旋流分离器是天然气加工处理工业的一大技术创新[2-3]，与常规的天然气处理技术相比，具有投资少、效率高、能耗低、无污染、体积小等优点[4-7]。

天然气在超声速旋流分离器内的流动是一个典型的多组分、可压缩、有相变气体的超声速流动过程，而Laval喷管正是实现这一过程的核心部件。截至目前，国内外学者对Laval喷管内部的凝结相变现象开展了大量研究工作。Gyarmathy[8]在气-液两相间传热、传质及动量交换的基础上，建立了可以预测液滴生长率、表面温度及变化速率的数学模型。Young[9-10]推导出了适用于任意Knudsen数的纯蒸汽和含惰性气体蒸汽凝结流动的液滴生长率公式。荷兰的Endhoven大学van Dongen教授课题组对成核脉冲膨胀装置(Nucleation pulse expansion tube)内双组分与多组分体系的凝结过程进行了较为系统的研究[11-15]。李亮等[16]、巫志华等[17]在单组分可压缩凝结超声速流动的数学模型、数值求解技术等方面开展了较为深入的研究工作。杨勇等[18-19]通过分析蒸汽超声速流动过程中的二维边界效应，研究了凝结激波的形成机理。当前，对于超声速凝结特性的研究主要围绕某一种可凝气体的凝结特性展开，由于双可凝气体凝结过程与单可凝气体相比更加复杂，目前对其凝结相变研究较少，相应的实验数据较单可凝数据也较少，只有Endhoven大学相关学者利用成核脉冲膨胀装置做过相关研究[13]，但该装置与Laval喷管结构存在较大差别。笔者通过建立Laval喷管内超声速凝结流动数学模型，以空气+水+乙醇为介质研究Laval喷管内三组分(双可凝)气体超声速凝结特性，分析了入口参数对超声速凝结过程的影响，并通过与空气+水双组分(单可凝)气体对比，研究了第二种可凝组分对混合气体凝结的影响。

1 Laval喷管结构设计

Laval喷管主要包括入口段、渐缩段、喉部及渐扩段4部分[20-21]。采用BWRS真实气体状态方程[7]，编程计算气体热力学性质，结合实验条件下压缩机内气体压力、温度及临界流量参数，计算求得Laval喷管喉部半径为2.5 mm。将稳定段直径与喉部直径之比取为7～8，稳定段长度取为喉部直径的10倍左右，入口段半径为20 mm，长度为50 mm；渐缩段采用双三次曲线设计，通过该线型获得的流场涡流小，过渡平稳，渐缩段长度为56 mm；喉部采用一段平缓光滑的圆弧作为过渡曲线；渐扩段采用等膨胀率设计，膨胀率取为10000 s-1，长度为71.28 mm，渐扩段出口半径为6.15 mm。考虑到实验加工方便，且能够更加直观地观察Laval喷管内部的流场分布情况，所设计Laval喷管截面采用矩形截面，三维结构如图1所示。

图1 Laval喷管三维结构示意图Fig.1 Schematic diagram of 3D structure of the Laval nozzle

2 超声速凝结流动数学模型

2.1 凝结流动控制方程

采用欧拉双流体模型，控制方程包括气相流动方程和液相流动方程。建立气液两相流动控制方程时，同时考虑了气液相间滑移的影响以及传热传质的作用，各方程中加入了由于凝结作用产生的源相[22-23]。

(1)气相流动控制方程组见式(1)～(4)。

(1)

(2)

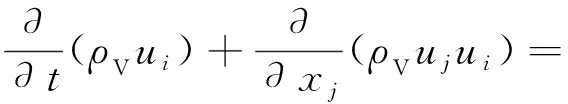
(3)

(4)

(2)液相流动控制方程组见式(5)～(7)。

(5)

(6)

(7)

(3)源项方程组见式(8)～(16)。

Sm=-(m1+m2)

(8)

Sm2=-(m3+m4)

(9)

Su=-(m1+m2)ui

(10)

Sh=(m1+m2)(hLV-h)

(11)

SY=m1+m2

(12)

(13)

(14)

m3=a2M2m1/(a2M2+a1M1)

(15)

m4=b2M2m2/(b2M2+b1M1)

(16)

2.2 三组分气体热力学关系

混合气体中，a1、a2和b1、b2可分别表示为：

(17)

(18)

最大摩尔分数amax1、amax2可以表示为：

(19)

(20)

混合物的密度ρ可表示为：

(21)

ρa=(1-amax1-amax2)ρ

(22)

ρV1=(amax1-a1)ρ,ρV2=(amax2-a2)ρ

(23)

设初始时刻气体的定容热容为Cv0，定压热容为Cp0，气体常数为R0，则表达式为：

Cv0=(1-amax1-amax2)Cva+amax1CvV1+amax2CvV2

(24)

Cp0=(1-amax1-amax2)Cpa+amax1CpV1+amax2CpV2

(25)

R0=(1-amax1-amax2)Ra+amax1RV1+amax2RV2

(26)

凝结过程中，上述表达式转变为：

Cv1=(1-b1-b2)Cva+b1CvV1+b2CvV2

(27)

Cp1=(1-b1-b2)Cpa+b1CpV1+b2CpV2

(28)

R1=(1-b1-b2)Ra+b1RV1+b2RV2

(29)

忽略凝结液滴所占体积，混合物的压力和总焓可分别表示为：

p=ρT〔(1-b1-b2)Ra+b1RV1+b2RV2〕

(30)

h=Cp0T-a1h1-a2h2

(31)

2.3 液滴成核和生长模型

蒸汽的凝结过程主要包括液滴成核与生长两个阶段。蒸汽进入Laval喷管，随着蒸汽的不断膨胀，过饱和度增大到一定程度，大量凝结核会瞬间产生，即为液滴成核阶段。临界凝结核产生后，更多的蒸汽会在凝结核表面不断生长，即为液滴生长阶段。

液滴成核模型采用文献[24]中提出的双组分气体自发成核模型修正方法，该方法通过考虑真实气体效应进行化学势差及膨胀率计算，对经典成核理论模型进行了修正。

液滴生长过程采用Gyarmathy液滴生长模型，由于临界核心半径很小(微米级)且均匀分布在气相中，彼此碰撞概率很低，因此仅考虑单一液滴与周围气体的传热，忽略液滴之间的聚并与破碎。模型中液滴与气体间的传热系数可由式(32)进行计算[25]。

(32)

依据传热、传质过程，可推导得到液滴生长速率计算模型，见式(33)。

(33)

由于多组分气体不存在压力对应的饱和温度Ts这一概念，将三组分相图中露点线类比于单组分中饱和曲线。

2.4 湍流模型和计算方法

Laval喷管内气体流动属高速可压缩流动，选择适用于壁面束缚流动及可压缩流体流动的k-ω湍流模型计算雷诺应力项以封闭控制方程组。采用密度基方法进行求解，流动控制方程组、湍流动能方程、湍流耗散率方程均采用二阶迎风格式进行离散。

利用C语言编写用户自定义函数UDF添加各方程源项，并通过用户自定义标量UDS输运方程在FLUENT中增加液相流动控制方程组。

2.5 网格划分和边界条件

采用非结构化网格对Laval喷管进行网格划分。考虑到边界层的影响，对边界层进行局部加密，Laval喷管网格及边界条件设置如图2所示。选择Laval喷管轴线处成核速率、液滴半径、液滴数量以及湿度作为敏感特征参数开展网格独立性验证，进一步保证计算的精度。结果表明，当网格大于141669时，误差基本控制在0.2%范围内，可以保证计算的精度。因此，最终确定Laval喷管的网格数为141669。

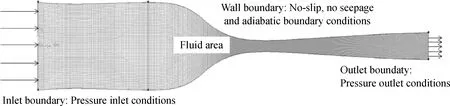
图2 Laval喷管网格及边界条件Fig.2 Grid and boundary conditions of the Laval nozzle

3 三组分气体凝结流动特性数值模拟

3.1 Laval喷管内的凝结流动现象

Laval喷管入口可凝组分默认为饱和状态，对空气+水+乙醇体系在Laval喷管内的凝结过程进行研究，计算条件为：入口压力为0.6 MPa，温度为296 K，乙醇和水的摩尔比为80∶20，模拟结果如图3所示。

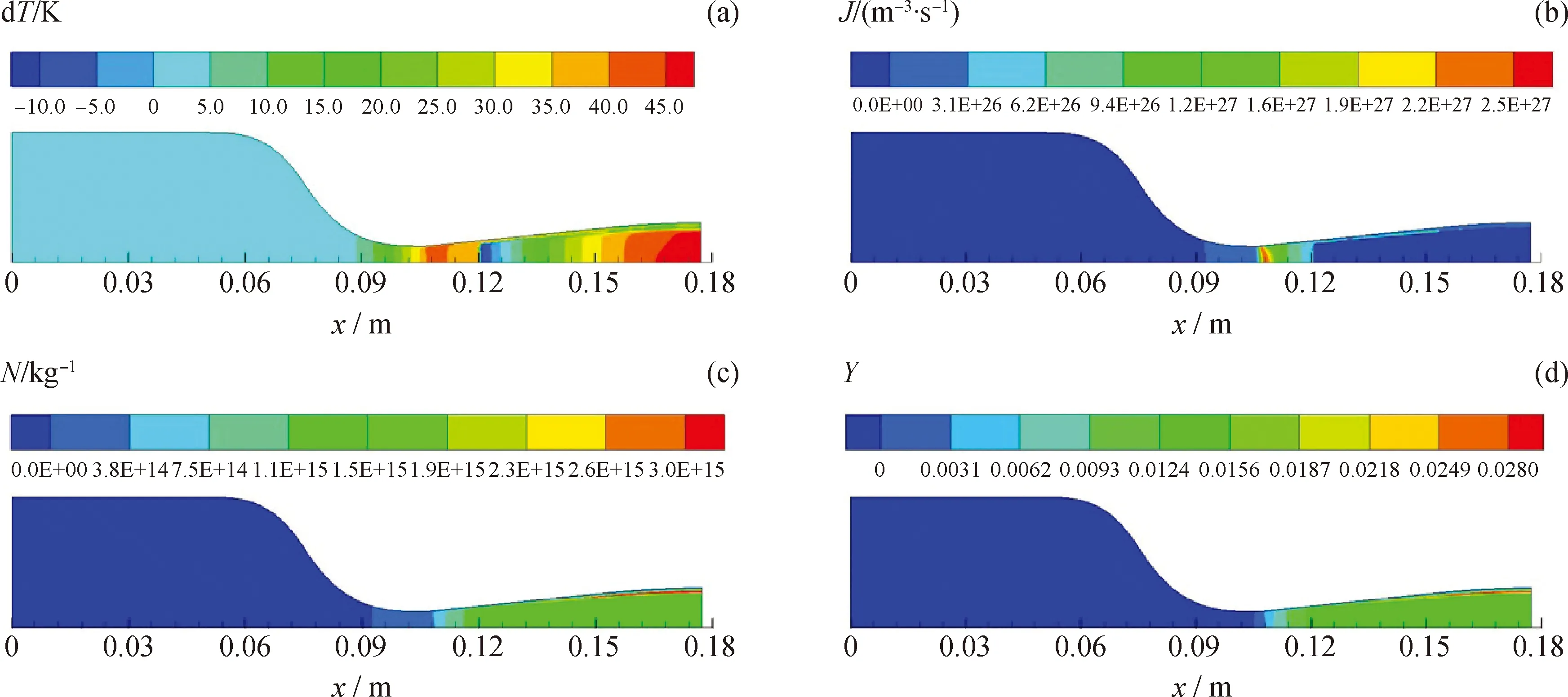
图3 Laval喷管内三组分气体凝结流动参数分布Fig.3 Condensation and flow parameter distributions of ternary mixture in the Laval nozzlepin=0.6 MPa; Tin=296 K; n(Alcohol)∶n(Water)=80∶20(a) dT; (b) J; (c) N; (d) Y

从图3可以看出，气体流过Laval喷管喉部后，由于Laval喷管内温度、压力不断降低，过冷度不断升高，部分可凝气体发生凝结，Wilson点出现(约在喉部之后3.5 mm处)。在过冷度最大值附近，成核率急剧增大(最大值约为2.57×1027/(m3·s))，出现大量凝结核心。相应地，液滴数与湿度迅速增加并很快达到稳定值，在出口液滴数约为1.9×1015/kg，湿度约为1.3×10-2。

3.2 气体组成对凝结流动的影响

在入口压力为0.6 MPa、入口温度为296 K条件下，分别选取不同比例的空气、水与乙醇组成的三组分体系，研究气体组成对凝结过程的影响，结果见图4。从图4可以看出，随着混合体系中乙醇含量的升高，成核位置不断向喉部方向移动，这是因为随着乙醇含量的升高，相包络线向高温方向移动，气体将在更高温度下发生凝结，更易达到Wilson点。同时，随着乙醇含量的升高，Laval喷管内成核率、液滴数均增大，但成核区收窄，液滴生长区向前移动，说明易凝组分的增多可促进结晶核心的出现，而在成核率达到最大时，凝结释放的潜热又会破坏成核环境，使成核区收窄。此外，随着乙醇含量的升高，液滴生长速率的最大值增大，Laval喷管出口湿度相应升高，说明液滴生长公式中潜热较比热比的影响更加明显，即凝结潜热对三组分气体生长速率的变化起着主导作用。因此，提高潜热较小组分的含量，可以促进混合气体的凝结，增大Laval喷管出口的湿度。

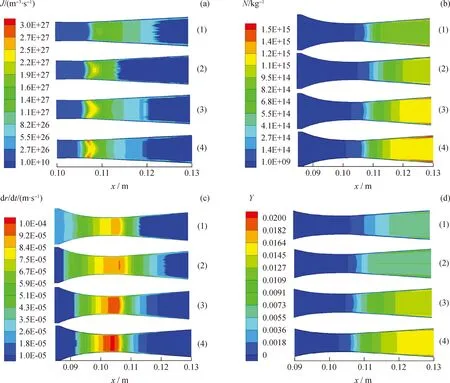
图4 Laval喷管内不同组成条件下三组分气体凝结参数分布Fig.4 Condensation parameter distributions of ternary mixture in the Laval nozzle under different composition conditionspin=0.6 MPa; Tin=296 K(a) J; (b) N; (c) dr/dt; (d) Yn(Alcohol)∶n(Water): (1)60∶40; (2)70∶30; (3) 80∶20; (4) 90∶10

3.3 入口温度对凝结流动的影响

为研究入口温度对三组分气体超声速凝结流动的影响，设置Laval喷管入口压力为0.6 MPa，乙醇和水的摩尔比为80∶20，模拟结果如图5所示。由图5可知，在入口可凝组分饱和的情况下，当入口温度从286 K升高到306 K，Wilson点向喉部移动，凝结更易发生；成核率最大值随入口温度的升高而增大，出口湿度也随之增大(最大成核率从2.15×1027/(m3·s)增大到3.01×1027/(m3·s)，出口湿度从8.0×10-3增大到2.63×10-2)，这是因为入口温度越高，可凝组分的饱和蒸气压越大，在气体混合物中的含量越高。此外，液滴生长速率与液滴半径随着入口温度的升高而增大(最大液滴生长速率从2.15×10-5m/s增大到2.31×10-4m/s，最大液滴半径从1.49×10-7m增大到1.94×10-7m)。

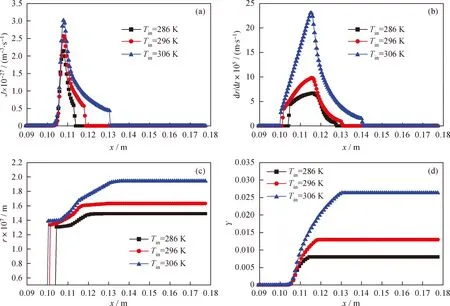
图5 Laval喷管内不同入口温度(Tin)条件下三组分气体凝结参数分布Fig.5 Condensation parameter distributions of ternary mixture in the Laval nozzle at different inlet temperatures (Tin)pin=0.6 MPa; n(Alcohol)∶n(Water)=80∶20(a) J; (b) dr/dt; (c) r; (d) Y

3.4 入口压力对三组分气体凝结流动的影响

为研究入口压力对三组分气体超声速凝结流动的影响，设置Laval喷管入口温度为296 K，乙醇和水的摩尔比为80∶20，模拟结果如图6所示。由图6可知，入口压力对凝结流动的影响规律与入口温度类似，当入口压力从0.4 MPa增大到0.8 MPa，Wilson点向喉部方向移动，凝结更易发生，成核率最大值随之增大，出口湿度随之减小(最大成核率从1.96×1027/(m3·s)增大到2.96×1027/(m3·s)，出口湿度从9.8×10-3增大到1.96×10-2)；液滴半径随着入口压力的升高而减小(最大液滴半径从 1.73×10-7m减小到1.57×10-7m)；液滴生长速率差别不大(10-4m/s左右)，这是因为，入口压力越高，可凝组分分压越小、含量越低，但高压条件又促进了液滴的生长，二者的综合作用导致随着压力的变化液滴生长速率无明显改变。

3.5 第二种可凝组分对三组分气体凝结成核的影响

在入口温度296 K、入口压力0.6 MPa条件下，通过对比空气+水(水为气体饱和态)、空气+水+乙醇(乙醇和水的摩尔比为80∶20，乙醇和水为气体饱和态)的凝结过程，结果如图7所示。由图7可以发现，三组分气体凝结过程更容易发生，其液滴生长速率、液滴半径、成核率和出口湿度均明显高于双组分气体(空气+水、空气+水+乙醇体系液滴生长速率分别为1.65×10-5m/s和1.02×10-4m/s，最大液滴半径分别为1.32×10-7m、1.63×10-7m，最大成核率分别为9.46×1026/(m3·s)、2.57×1027/(m3·s)，出口湿度分别为9.8×10-4、1.3×10-2)。这说明，对于可凝组分液相互溶的三组分气体发生凝结时，两种可凝气体的凝结过程是相互促进的，其凝结机理可以用图8表示。在空气+水+乙醇组成的三元体系中，乙醇先于水蒸气发生大量成核，随着过冷度的继续增加，水蒸气也产生了凝结，混合体系实质上存在水与乙醇两种凝结核心，乙醇蒸气和水蒸气在两种凝结核心上均可以发生聚集。

图6 Laval喷管内不同入口压力(pin)条件下三组分气体凝结流动参数分布Fig.6 Condensation parameter distributions of ternary mixture in the Laval nozzle under different inlet pressures (pin)Tin=296 K; n(Alcohol)∶n(Water)=80∶20(a) J; (b) dr/dt; (c) r; (d) Y

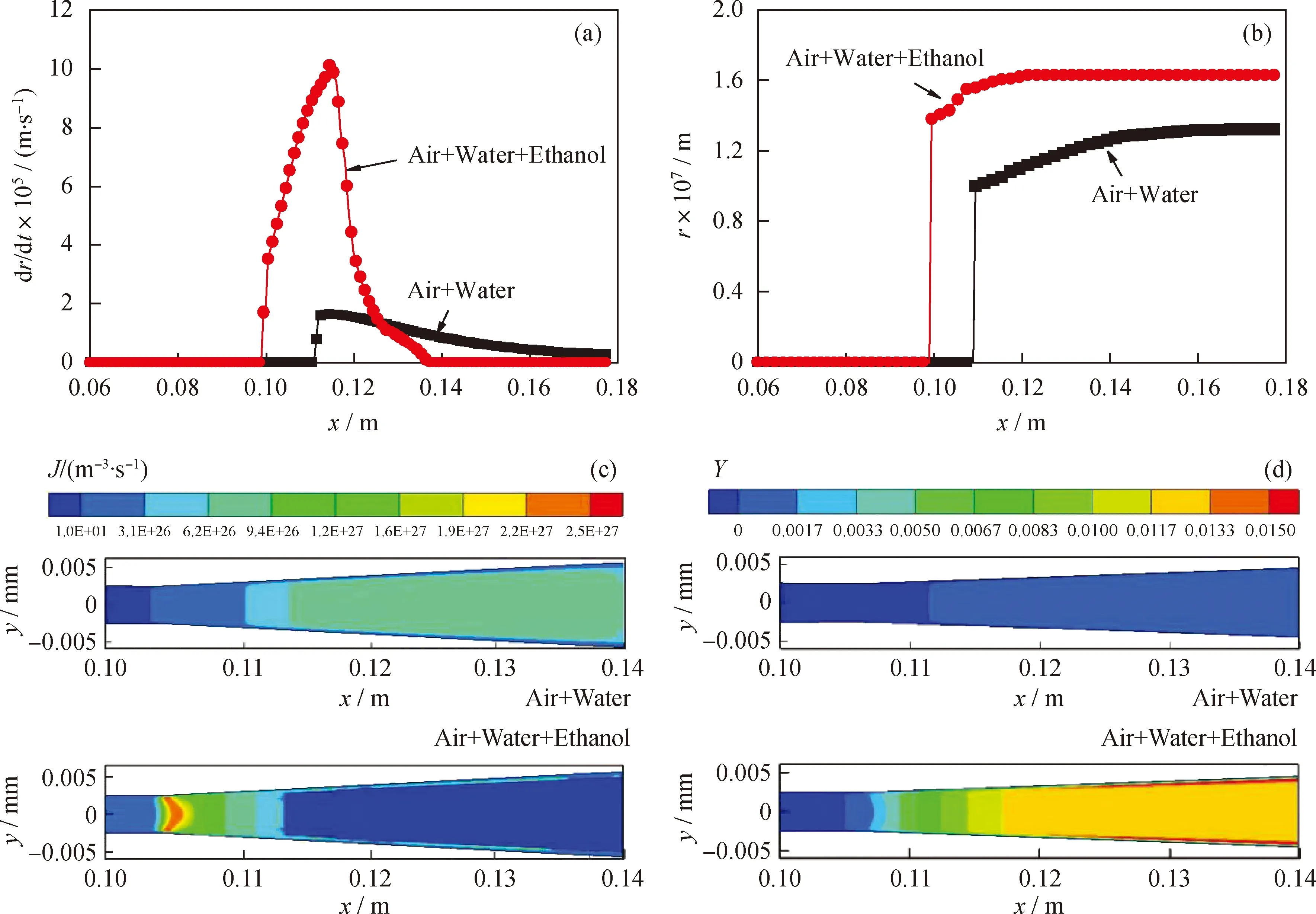
图7 Laval喷管内双组分与三组分气体凝结参数对比Fig.7 Comparison of condensation parameters of binary and ternary mixtures in the Laval nozzlepin=0.6 MPa; Tin=296 K(a) dr/dt; (b) r; (c) J; (d) Y

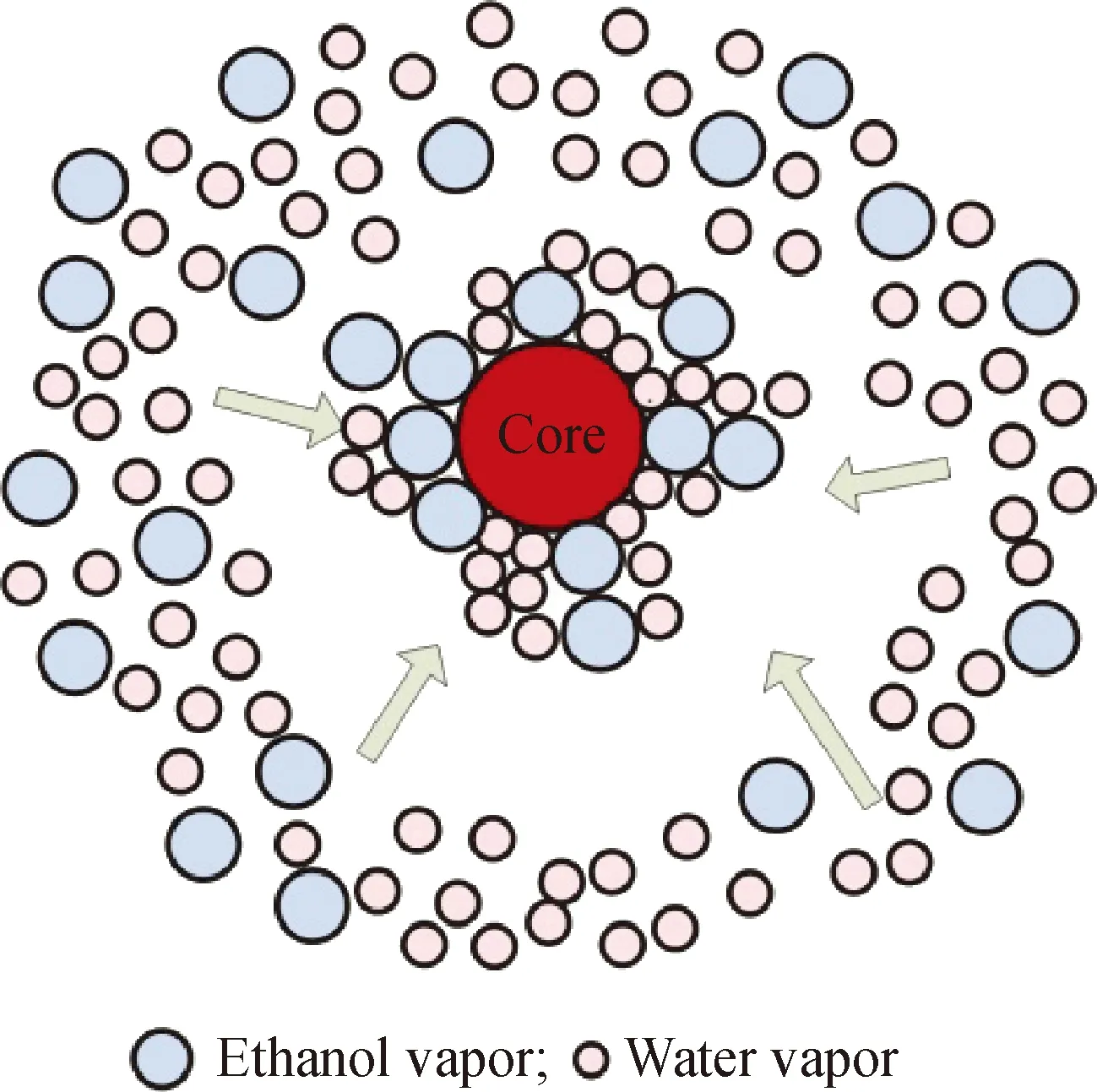
图8 Laval喷管内三组分气体超声速凝结机理Fig.8 Supersonic condensation mechanism ofternary mixture in the Laval nozzle

4 三组分气体凝结流动特性实验

通过开展室内实验来验证所建立数学模型及数值方法的可靠性，实验系统由主体系统和辅助系统组成，主体系统包括自行设计的Laval喷管系统、光学测试系统与分布式压力测试系统；辅助系统包括供气系统、计量系统、加湿系统以及光电转换与数据采集系统等，实验流程如图9所示，光电转换与数据采集系统原理如图10所示。

实验中介质为空气+水+乙醇，Laval喷管入口实验条件如表1所示。实验测得Laval喷管沿程压力、液滴半径、液滴数目分布与模拟结果对比分别如图11～13所示。

从图11可以看出，实验中由于分布式压力测量系统灵敏度有限，并未监测到凝结冲波现象，但实验压力分布与模拟情况基本一致，说明笔者建立的数学模型对流场预测与凝结成核研究具有较高的准确性。从图12可以看出，凝结起始位置的数值计算与实验基本吻合，从而进一步验证了数学模型对凝结起始位置的预测精度；分别对比两组实验数据还可以看出，当乙醇含量较高时，实测液滴数目更大，这也说明了乙醇含量较高时更易发生凝结，与3.2节中得出的结论一致。从图13可以看出，液滴数目实验数据分布规律与数值模拟基本相同，即在液滴生成后数目基本保持不变，说明在数值模拟中所做“忽略液滴的聚并与破碎”假设较为合理。

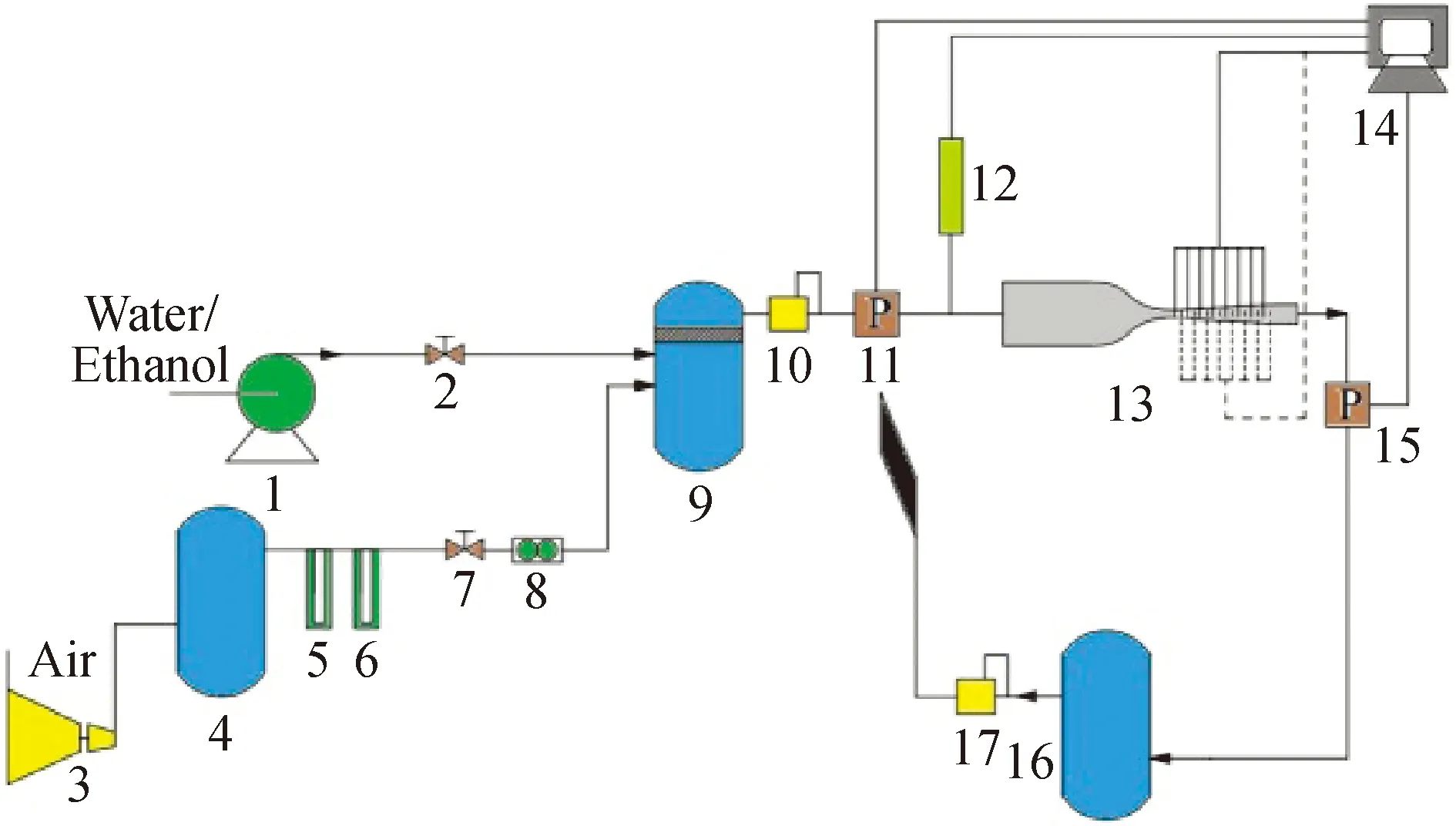
图9 三组分气体超声速凝结实验流程Fig.9Flowsheet of ternary mixture supersoniccondensation experimental apparatus1—High pressure micro mist humidifier; 2—Regulating valve;3—Screw compressor; 4—Gas buffer tank; 5,6—Filter;7—Electric control valve; 8—Vortex flowmeter;9—High pressure humidifying tank; 10,17—Self actuated regulator;11,15—Pressure transmitter; 12—Humidity sensor;13—Laval nozzle; 14—Data acquisition system;16—Buffer vent tank

图10 光电转换与数据采集系统原理Fig.10 Principle of photoelectric conversion anddata acquisition system

从液滴数目、液滴半径分布对比结果还可以看出，与模拟结果相比，实验所得液滴数目值偏小，液滴半径值偏大，分析产生误差的原因主要有：(1)超声速条件下测试装置对于液滴的捕捉存在难度，难以保证测量的精度；(2)尽管气体进入Laval喷管之前进行了杂质的过滤，但仍难以完全消除，从而造成Laval喷管内非均质凝结过程的产生，抑制了自发凝结过程，使得液滴数目偏小，液滴半径也偏大。

表1 Laval喷管入口实验条件Table 1 Experimental conditions at inlet of the Laval nozzle

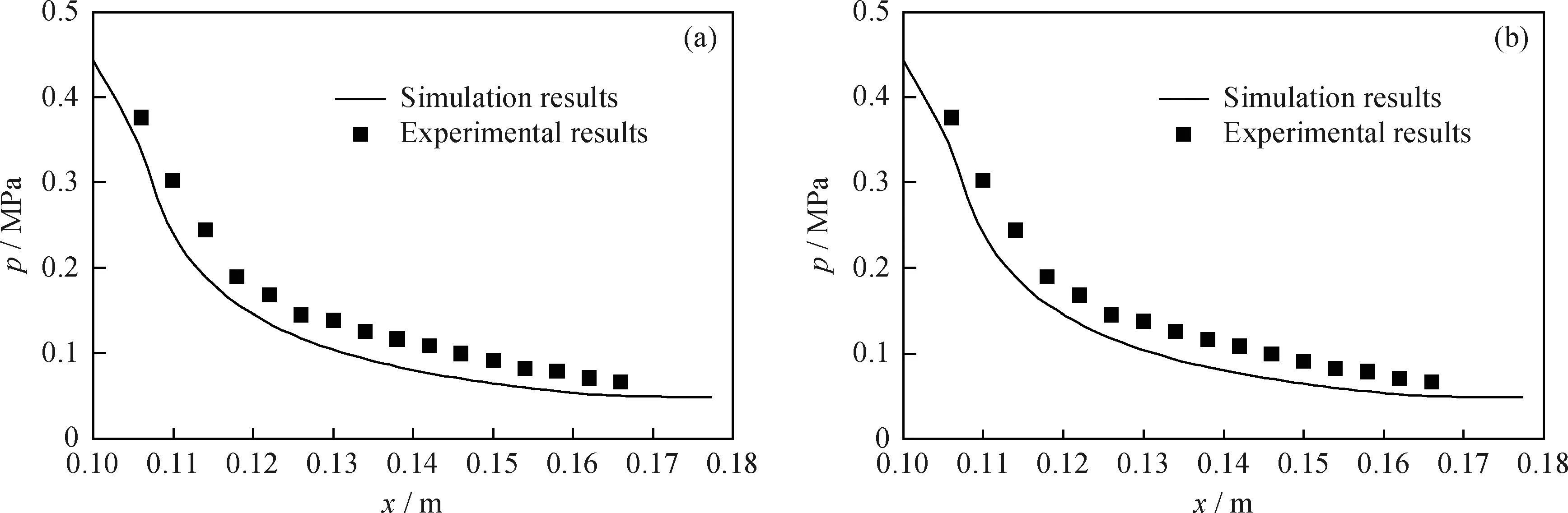
图11 Laval喷管内模拟计算和实验得到的压力(p)分布结果对比Fig.11 Comparison between simulation and experimental results of pressure(p) distribution in the Laval nozzle(a) Group 1; (b) Group 2

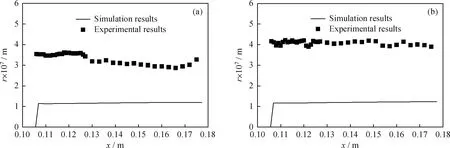
图12 Laval喷管内模拟计算和实验得到的液滴半径(r)分布结果对比Fig.12 Comparison between simulation and experimental results of droplet radius(r) distribution in the Laval nozzle(a) Group 1; (b) Group 2

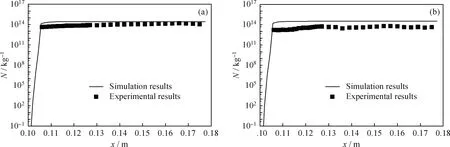
图13 Laval喷管内模拟计算和实验得到的液滴数目(N)分布结果对比Fig.13 Comparison between simulation and experimental results of droplet number(N) distribution in the Laval nozzle(a) Group 1; (b) Group 2

5 结 论

结合液滴成核与生长模型，以及气、液流动控制方程，对Laval喷管内三组分气体超声速流动条件下凝结流动特性与影响因素进行了数值计算与实验研究，得到以下结果。

(1)在入口可凝组分为饱和状态下，随着乙醇含量的升高，Laval喷管内成核率、液滴数均增大，但成核区收窄，液滴生长区向前移动，说明易凝组分的增多可促进凝结核心的出现，但在成核率达到最大时，凝结释放的潜热又会破坏成核环境，使成核区收窄；升高入口温度与压力均可以使Wilson点向喉部移动，促进凝结的发生，进而提高出口气体湿度。

(2)在空气+水+乙醇组成的三元体系中，乙醇先于水蒸气发生大量成核，随着过冷度的继续增加，水蒸气也产生了凝结，混合体系实质上存在水与乙醇两种凝结核心，乙醇蒸气和水蒸气在两种凝结核心上均可以发生聚集。

(3)通过实验得出的Laval喷管沿程压力分布及Wilson点结果与数值计算结果吻合较好，说明所建立的数学模型具有较高的准确性。但超声速条件下液滴数目与液滴半径实验精度较低，接下来的实验研究将通过改进实验测试手段，进一步提高超声速条件下液滴数与液滴半径测量精度。

符号说明：

a1、a2——所形成临界核中可凝组分1、2的摩尔分数，无量纲；

amax1、amax2——可凝组分1、2的最大摩尔分数，无量纲；

b1、b2——初始气相可凝组分1、2的摩尔分数，无量纲；

CpV1、CpV2——可凝组分1、2定压热容，J/(kg·K)；

Cv0、Cv1——初始时刻与凝结时刻气体的定容热容，J/(kg·K)；

CvV1、CvV2——可凝组分1、2的定容热容，J/(kg·K)；

dr/dt——液滴生长速率，m/s；

dT——过冷度，K；

E——总能，J/kg；

h——总焓，J/mol；

h1、h2——可凝组分1、2的凝结潜热，J/kg；

hLV——凝结潜热，J/kg；

J——成核率，m-3·s-1；

keff——有效导热系数，W/(m·K)；

kr——液滴与气体间的导热系数，W/(m·K)；

Kn——Kundsen数，无量纲；

m1、m2——成核、生长过程中单位时间内单位体积凝结的组分1的液滴质量，kg/(m3·s)；

m3、m4——成核、生长过程中单位时间内单位体积凝结的组分2的液滴质量，kg/(m3·s)；

M——混合气体的质量，kg；

M1、M2——可凝组分1、2的质量，kg；

Ma——空气的质量，kg；

ML1、ML2——可凝组分1、2的液相质量，kg；

MV1、MV2——可凝组分1、2的蒸汽质量，kg；

n——物质的量，mol；

N——液滴数目，kg-1；

p——压力，MPa；

pin——入口压力，MPa；

PrV——气体Prandtl数，无量纲；

Q——体积流量，m3/h；

rc——液滴临界半径，m；

r——液滴半径，m；

R0、R1——初始时刻与凝结时刻气体常数，J/(kg·K)；

Ra——空气气体常数，J/(kg·K)；

RV1、RV2——可凝组分1、2的蒸汽气体常数，J/(kg·K)；

Sh——能量源项，J/(m3·s)；

Sm——质量源项，kg/(m3·s)；

Sm2——可凝组分2的质量源项，kg/(m3·s)；

Su——动量源项，kg/(m2·s2)；

SY——湿度源项，kg/(m3·s)；

t——时间，s；

T——温度，K；

Tin——入口温度，K；

Ts——气体压力对应的饱和温度，K；

ui、uj——轴向与径向速度，m/s；

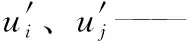
x——轴向坐标，m；

xi、xj——轴向与径向位置坐标，m；

y——径向坐标，m；

Y——湿度，无量纲；

γ——比热比，无量纲；

δij——Kronecker delta数，无量纲；

λV——气体导热系数，W/(m·K)；

μ——气体黏度，kg/(m·s)；

ρ——混合物密度，kg/m3；

ρa——空气密度，kg/m3；

ρL——液相密度，kg/m3；

ρL1——所形成临界核液相密度，kg/m3；

ρL2——液滴生长过程中凝结液相密度，kg/m3；

ρV——气相混合物密度，kg/m3；

ρV1、ρV2——可凝组分1、2蒸汽密度，kg/m3；

τeff——有效应力张量，无量纲。