催化裂化提升管反应器出口快分构件优化

武志俊， 李 强， 王振波， 徐嘉伟， 李安俊， 金有海

(中国石油大学(华东) 化学工程学院， 山东 青岛 266580)

催化裂化是我国炼油工业最重要的二次加工工艺，生产了国内约75%的汽油、30%的柴油和40%以上的丙烯[1]。催化裂化的产品如汽油、柴油等是裂化反应的中间产品，反应时间对产品的收率和分布具有决定性作用，而过长的反应时间会导致严重的二次反应和过裂化，造成产品收率降低、焦炭收率高等问题，严重时甚至导致装置结焦并停工。催化裂化提升管反应器上端设有气-固快分构件，其目的是使催化剂与油气快速分离以抑制反应的继续进行。催化裂化工艺中油气在提升管停留时间大概为2～4 s[2]，因此，快分构件需满足的条件为停留时间短、提高催化剂的分离效率、最大程度降低压降。研究并优化催化裂化提升管出口快分构件具有深远意义。

目前，国内外学者对催化裂化提升管反应器出口快分构件进行了大量的研究，核心技术主要被UOP等国外公司所掌握[3-7]，如UOP公司的闭式直连[3]和VDS(Virus detection system)、VSS(Visual source safe)技术[4-6]等。为改变这一现状，我国学者进行了大量的科研工作，掌握了一系列相关技术，并进一步实现了工业化[8-10]，结果显示该系列技术具有显著效果。目前我国催化裂化提升管出口一级分离器大多采用旋风分离器，曹占友等[11]提出了针对粗旋快分的FSC(Fender-stripping cuclone)和CSC(Circulating stripping cyclone)系统。我国催化裂化装置中有很大一部分采用内提升管反应器结构，在提升管出口连接多组旋风分离器，体积庞大的同时分离效率不稳定，卢春喜等[12]针对此类装置开发了VQS(Vortex quick separator)技术。在流场数值模拟研究的基础上，孙凤侠等[13-14]提出了SVQS(Super-vortex quick separator)系统。研究表明，FSC、VQS、和SVQS系统内油-剂分离的时间虽小于传统旋风分离器所用时间，但仍然长达5 s左右[14]。超短快分(Short resudence time separator, SRTS)是一种新型气-固分离装备，具有停留时间短、分离效率高、结构紧凑等优点[15]。严超宇等[16]采用数值模拟的方法对SRTS内流场进行了研究，刘显成等[17]通过实验对SRTS中心管直径、开缝宽度等几何尺寸进行了优化。

基于此，笔者以京博石化西区6.5×105t/a催化裂化装置的沉降器中粗旋为研究对象，调查现有提升管出口快分构件形式，分析其运行状况，并对现有构件进行优化。采用数值模拟方法，对京博石化粗旋内气相流场特性、颗粒轨迹以及分离效率等进行数值模拟与研究，然后提出优化模型并进行数值模拟，为催化裂化提升管反应器出口快分构件深入研究提供理论基础。

1 催化裂化装置沉降器粗旋几何模型建立

1.1 现场模型建立

参照京博石化西区6.5×105t/a催化裂化装置建立模型，采用Pro ENGINEER进行建模，结果如图1所示。图1(a)为沉降器内的粗旋，为左右2个并列放置，提升管反应器出来的油气从进气装置分左右两侧进入粗旋，经分离后，油气从排气管一侧的排气口进入细旋进行下一步分离，催化剂则从排尘管进入再生器再生再利用。模拟研究单个模型(如图1(b)所示)。

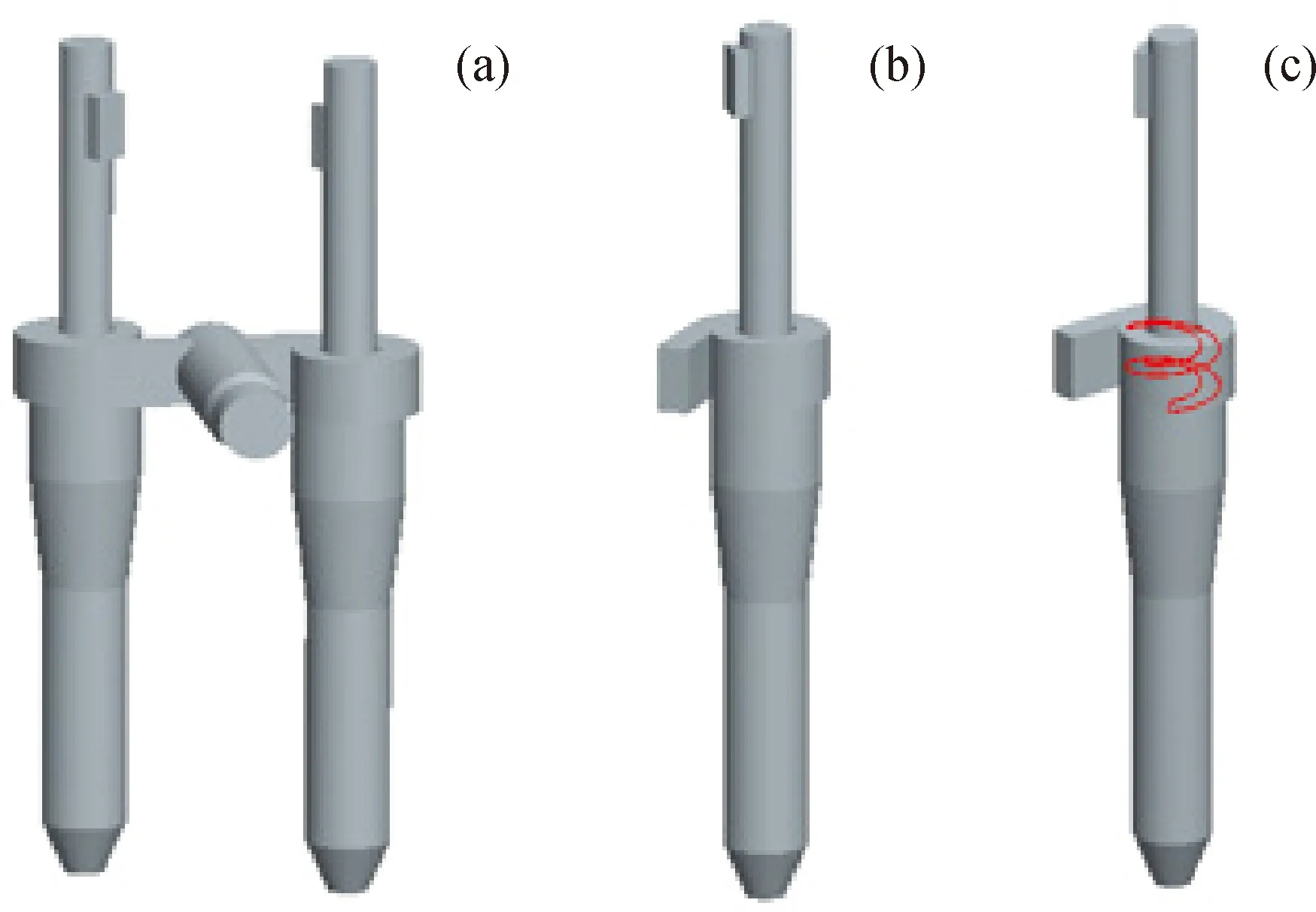
图1 催化裂化装置沉降器粗旋几何模型Fig.1 Geometric model of FCC settler separator(a) Field model; (b) Field single model; (c) Optimization model

1.2 优化方案及建模

旋风分离器分离的原理就是将携带催化剂的油气由直线运动变为螺旋运动，靠气流产生的离心力分离。但很多生产实践表明，仅靠圆筒壁的约束作用并不一定总能形成有效的螺旋运动，其分离效率也就不能保证。本次优化从旋风分离器原理入手，在排气芯管伸入混合腔部分加装导流板，目的就是引导和强制携带催化剂的油气做强旋转运动。

图1(c)所示为优化后的模型，红色部分为所加的导流板，参考文献[18]及结合现场实际，导流板倾角选取10°，螺距选取400 mm[19]，高度为600 mm。图2所示为沉降器粗旋的结构尺寸，为方便表达，建立坐标系，坐标原点为排气芯管与混合腔交界面的圆心，x、y、z分别为坐标轴的正方向。

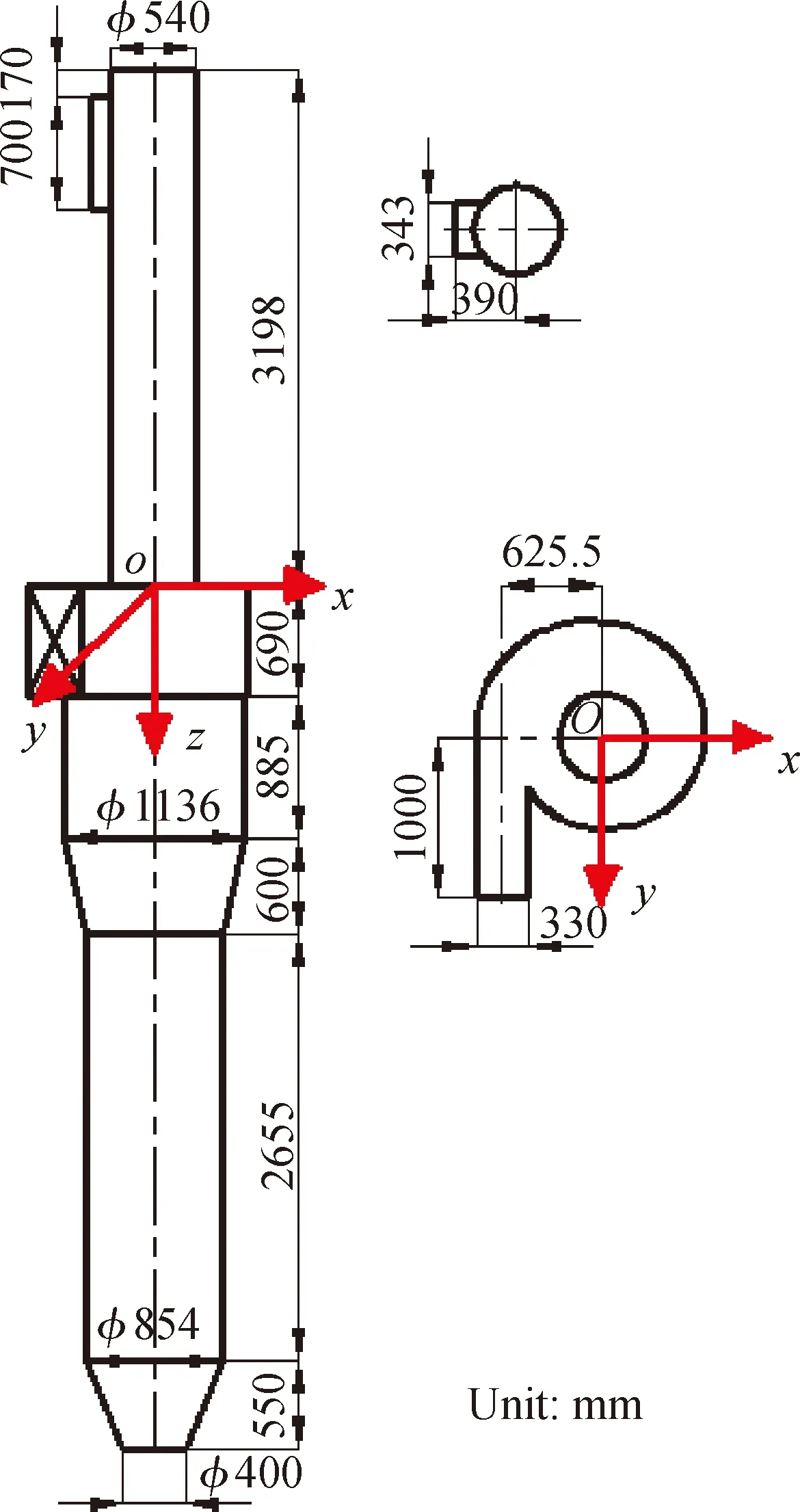
图2 催化裂化装置沉降器粗旋结构尺寸Fig.2 Structure size of FCC settler separator

2 催化裂化装置沉降器粗旋几何模型网格划分及参数设置

2.1 网格划分

为了生成质量较高的网格，采用结构化网格，需要将其依照尺寸的变化分为几部分进行划分，其中圆柱和锥形部分采用铜钱形布局。

2.2 数值模型的选择

采用雷诺应力模型，该模型抛弃了涡黏性假设，而是求解雷诺应力微分输运方程，更加严格地考虑各种力的快速变化，精度更高，尤其是提高了对复杂流动的精度。Fluent中有多种多相流模型，本次模拟采用DPM(离散相模型)模型，该模型适用于小颗粒、低浓度的条件。计算过程中先使用欧拉方程对气相进行计算，然后在此基础上使用拉格朗日方程对固相进行计算。

2.3 边界条件设置

2.3.1 入口边界条件设置

本次模拟将含颗粒气流入口边界条件设置为压力入口[20]。由于现场关于油气流量的数据只有处理量为65～70 t/h，为了获得油气的入口速度，参考了文献[21]，该文献中处理量为6250 kg/h，计算得到的产物流量为1708.86 m3/h，本次模拟处理量取68 t/h，类似得到流量Q=5.16 m3/s。沉降器粗旋模型的油气入、出口都是矩形，尺寸分别为入口：长a1=0.690 m,宽b1=0.330 m;出口：长a2=0.700 m,宽b2=0.343 m。

由式(1)计算可得入口速度vin=11.33 m/s。

(1)

该装置设计年生产能力为6.5×105t/a，按每年运行8000 h计算，生产量为81.25 t/h，结合查阅资料，粗旋的入口速度一般为10～20 m/s[22]，故本次模拟做4组对比实验，其进口速度分别为10、12、15和18 m/s。横向对比不同进口速度下粗旋的分离效率以及压降等参数。

现场没有入口处的压力值，有提升管下部压力1.7 MPa，以及沉降器顶部压力1.2 MPa，根据催化裂化工艺可知入口处压力值介于两者之间，取静压pS=1.5 MPa，动压pD计算公式见式(2)，总压p为静压与动压之和。水力直径Hd(m)、雷诺数Re、湍流强度I计算公式分别见式(3)、(4)、(5)。

(2)

(3)

(4)

I=0.16×Re-0.125

(5)

式(2)～(4)中，ρ为油气密度，kg/m3；l为特征长度，m；μ为动力黏度，N·s/m2。

表1为不同入口速度下粗旋的入口相关参数。

表1 不同入口速度下催化裂化装置沉降器粗旋入口边界条件Table 1 Entrance boundary condition data of FCC settler separator model at different entrance speeds

2.3.2 出口边界条件设置

将油气出口边界条件设置为速度出口，除速度外其余参数与入口参数算法相同。出口速度vout计算公式见式(6)。相关参数如表2所示。

表2 不同入口速度下催化裂化装置沉降器粗旋出口边界条件数据Table 2 Exit boundary condition data of FCC settler separator model at different entrance speeds

3 催化裂化装置沉降器粗旋模型模拟结果与分析

3.1 催化裂化装置沉降器粗旋内气相速度分布

3.1.1 切向速度分布

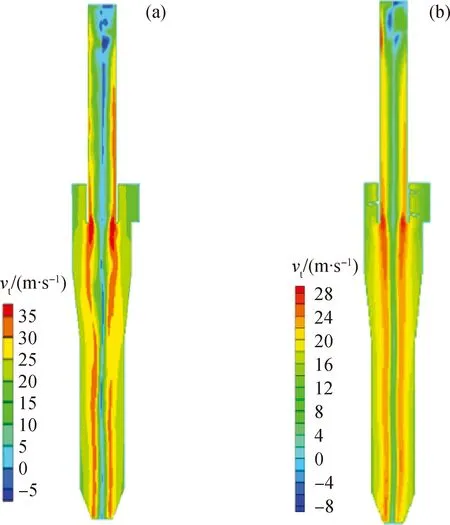
图3 催化裂化装置沉降器粗旋的现场模型和优化模型的切向速度(vt)云图Fig.3 Tangential velocity (vt) nephogram of field model andoptimization model of FCC settler separator vin=12 m/s; y=0(a) Field model; (b) Optimization model

图4为模型优化前后z=0.3 m和z=1.5 m截面的切向速度分布图。从图4可以看出，模型优化前后切向曲线均基本呈轴对称分布的“驼峰”型，也从侧面说明了旋风分离器内部流场为强旋转流场。流体的大部分数值为正值，部分负值说明出现了二次流。最大切向速度点形成圆柱形的分界面，在分界面的两侧将旋风分离器内部流场分为外部的准自由涡和中心处的准强制涡。由于中心处准强制涡的出现，使得粒子更加容易被甩向壁面，而外部准自由涡的出现则有利于颗粒在壁面被旋风分离器捕集。排气管上端出现突变是由于排气口设在一侧的原因。

3.1.2 轴向速度分布

图5为催化裂化装置沉降器粗旋现场模型和优化模型的轴向速度云图。从图5可以看出，其为轴对称分布，外层速度向下，内层速度向上，且内层向上速度的绝对值大于外层的。其中外层向下的轴向速度将碰到壁面的颗粒带到灰斗，有利于气-固的分离。

图6为催化裂化装置沉降器粗旋现场模型和优化模型z=0.3 m和z=1.5 m截面的轴向速度分布图。从图6可以看出，除外壁分离区外，随着半径的减小，轴向速度逐渐减少到零，随着半径的进一步减小[24]，轴向速度反向增大，呈“马鞍形”分布。现场模型中z=1.5 m截面中轴向速度曲线比较异常，原因应该是锥面段速度变化较大，流动比较复杂，故该种现象是正常的。

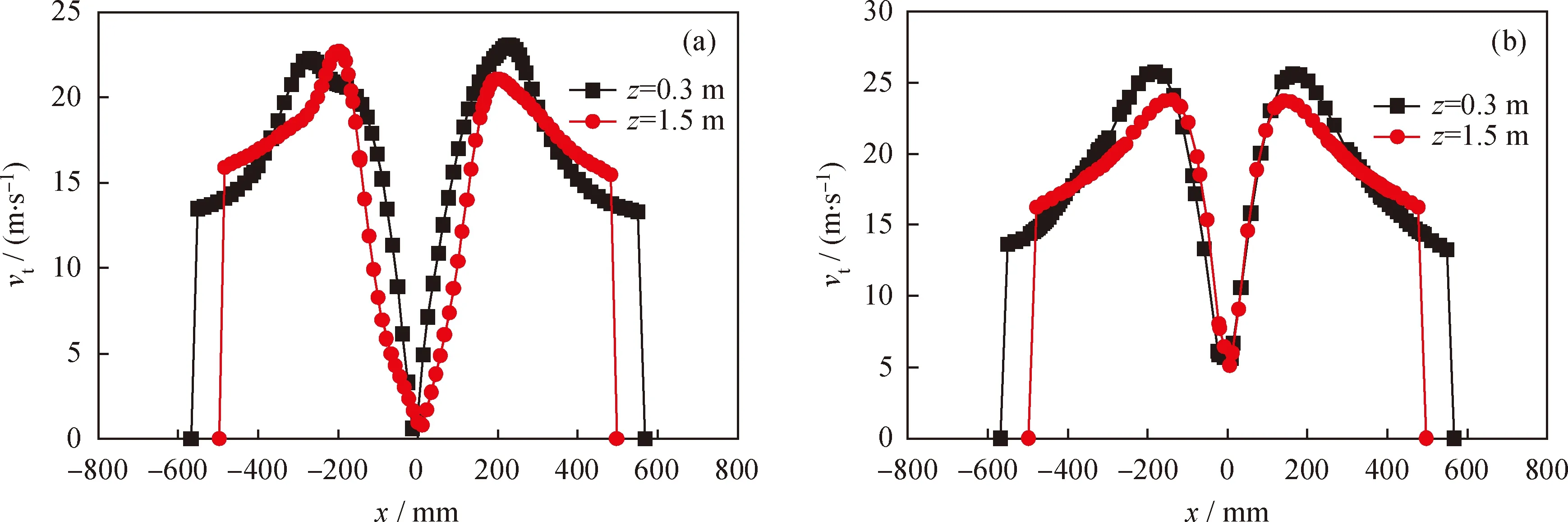
图4 催化裂化装置沉降器粗旋现场模型和优化模型的切向速度(vt)在x方向的分布Fig.4 Tangential velocity (vt) of field model and optimization model of FCC settler separatorvin=12 m/s; y=0(a) Field model; (b) Optimization model

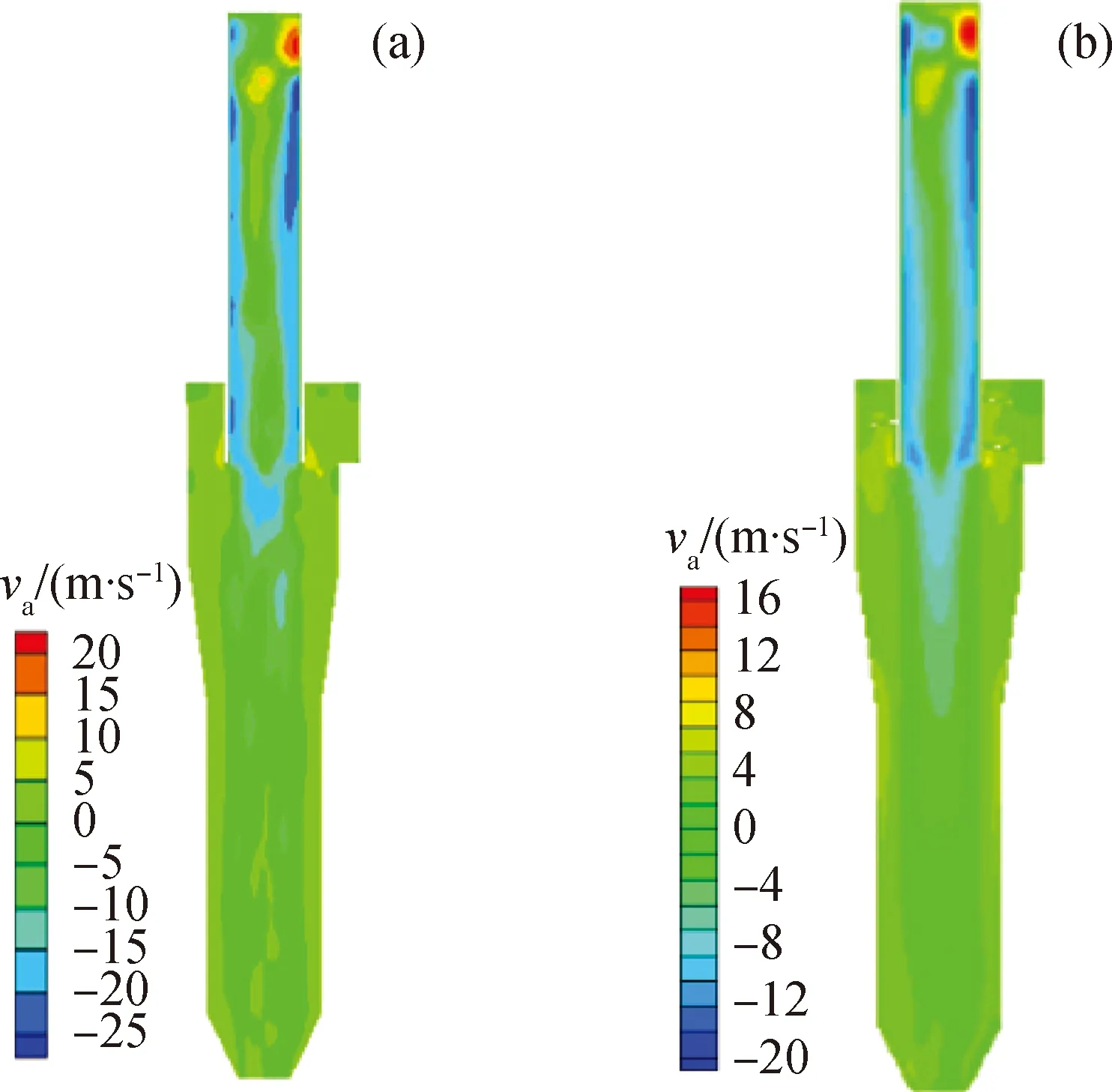
图5 催化裂化装置沉降器粗旋的现场模型和优化模型的轴向速度(va)云图Fig.5 Axial velocity (va) nephogram of field model andoptimization model of FCC settler separatorvin=12 m/s; y=0(a) Field model; (b) Optimization model

3.1.3 现场模型和优化模型速度分布对比

(1)切向速度对比

对比图4(a)和(b)中z=0.3 m处切向速度可以看出，现场模型和优化模型的切向速度沿径向分布规律变化不大，均呈现“驼峰”分布，优化模型的切向速度比现场模型的有较明显的增大，尤其是在峰值两侧，也就是气-固分离区域，有着明显的提高，这将有利于气-固两相的分离。

赵拥军 男，1964年出生于河南封丘，博士.现为解放军信息工程大学导航与空天目标工程学院教授、博士生导师，主要研究方向为雷达信号处理和阵列信号处理.

(2)轴向速度对比

对比图6(a)和(b)中z=0.3 m处轴向速度可以看出，现场模型和优化模型的外侧气流即旋转向下的“外旋流”差别不大，主要不同在于轴中心区域，优化模型的轴向速度比现场模型小，“内旋流”在进入排气管时会发生紊流现象，因此，降低其轴向速度可减少紊流现象，从而减少能量的损耗。

3.1.4 入口速度对切向速度和轴向速度分布的影响

图7为不同入口速度对优化模型切向速度和轴向速度的影响。由图7(a)可以看出，随着入口速度的增大，切向速度也随着增大，从而有利于旋风分离器内气-固两相的分离。由图7(b)可以看出，当进口速度为12 m/s、15 m/s、18 m/s时，其轴向速度曲线类似，相比10 m/s时，其峰值出现的位置向内侧移动，且峰值增大，更加有利于旋风分离器内气-固两相的分离。另外，轴向速度的零速包络面位置并不随进口速度的变化而改变。

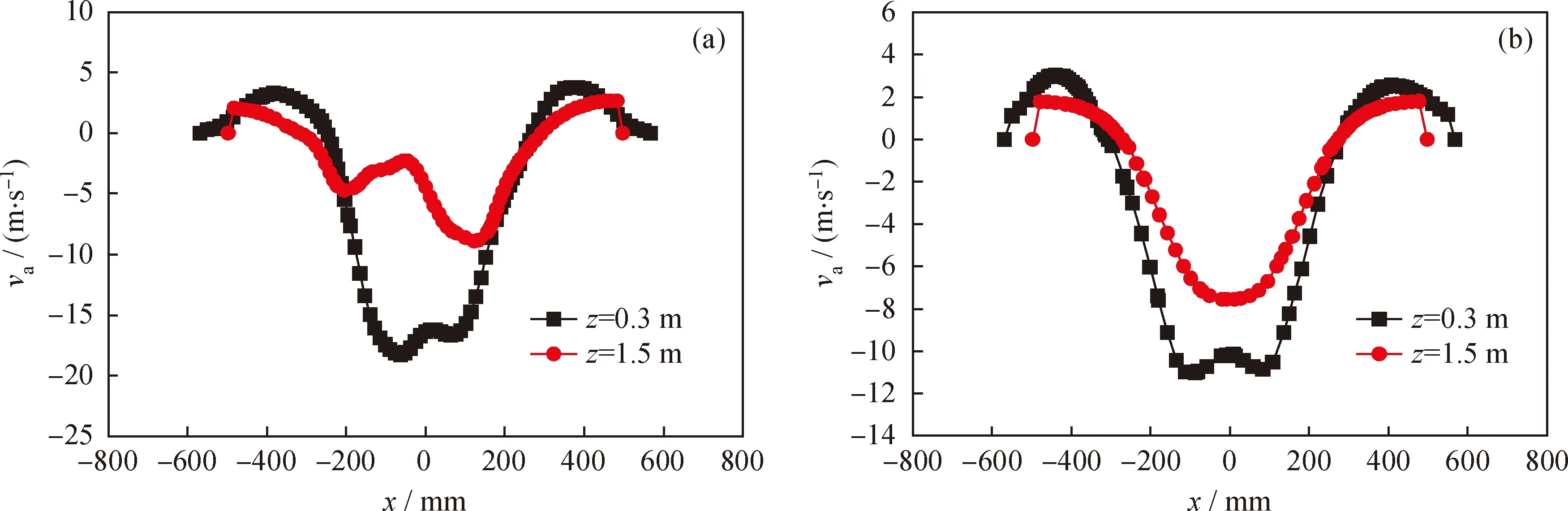
图6 催化裂化装置沉降器粗旋现场模型和优化模型的轴向速度(va)分布Fig.6 Axial velocity (va) of field model and optimization model of FCC settler separator vin=12 m/s; y=0(a) Field model; (b) Optimization model

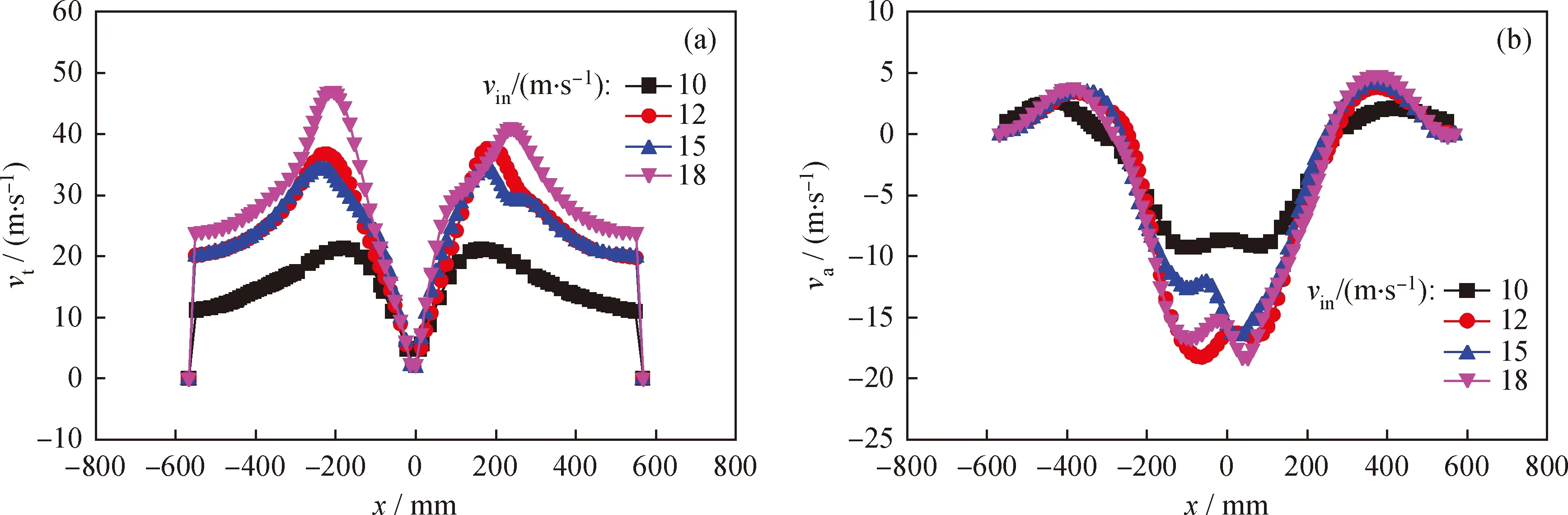
图7 入口速度(vin)对催化裂化装置沉降器粗旋优化模型切向速度(vt)和轴向速度(va)分布的影响Fig.7 Effects of inlet velocity (vin) on tangential velocity (vt) and axial velocity (va) of the optimized FCC settler separator model(a) vt; (b) va

3.2 催化裂化装置沉降器粗旋内压力分布

3.2.1 总压分布

由表1可知，动压pD比静压pS在数值上小4个数量级，总压可近似认为与静压相等，因此本次模拟只研究动压分布。

图8为催化裂化装置沉降器粗旋现场模型和优化模型总压分布云图。从图8可以看出，总压整体分布比较对称，沿轴向方向基本不发生变化，主要是沿径向发生变化，壁面处压力很高，之后沿着径向方向发生突降，为速度增大的原因。在颗粒捕集处，压力很低，容易发生滞留或返混现象。

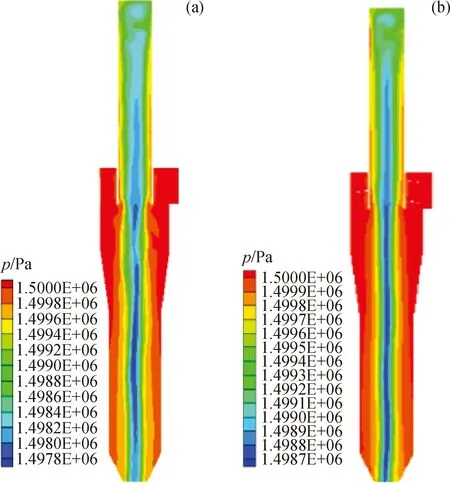
图8 催化裂化装置沉降器粗旋现场模型和优化模型的总压(p)云图Fig.8 Total pressure (p) nephogram of the field model andthe optimization model of FCC settler separator(a) Field model; (b) Optimization model

图9为入口速度为12 m/s时，z=0.3 m处模型优化前后总压沿径向分布图。从图9可以看出，压力沿径向呈轴对称分布，壁面处压力很高，随着半径的减小，压力值逐渐降低，直到某一位置发生突降，这种现象主要是由于中间部位速度较快造成的。

图9 催化裂化装置沉降器粗旋现场模型和优化模型z=0.3 m处总压(p)沿径向分布图Fig.9 Total pressure (p) distribution diagram of thefield model and the optimization model ofFCC settler separator at z=0.3 mvin=12 m/s; y=0

3.2.2 现场模型和优化模型压降的分布

压能是一种非常宝贵的能量，因而压降为衡量粗旋性能的一种重要标准，下面就对压降进行相关分析研究。

图10为催化裂化装置沉降器粗旋现场模型和优化模型压降分布图。从图10可以看出，在任意特定入口速度条件下，现场模型和优化模型压降都变小，并且随着入口速度的增大，压降降低的幅度也逐渐增大。从压降这一衡量标准来说，该粗旋经过优化后，性能得到了提升。

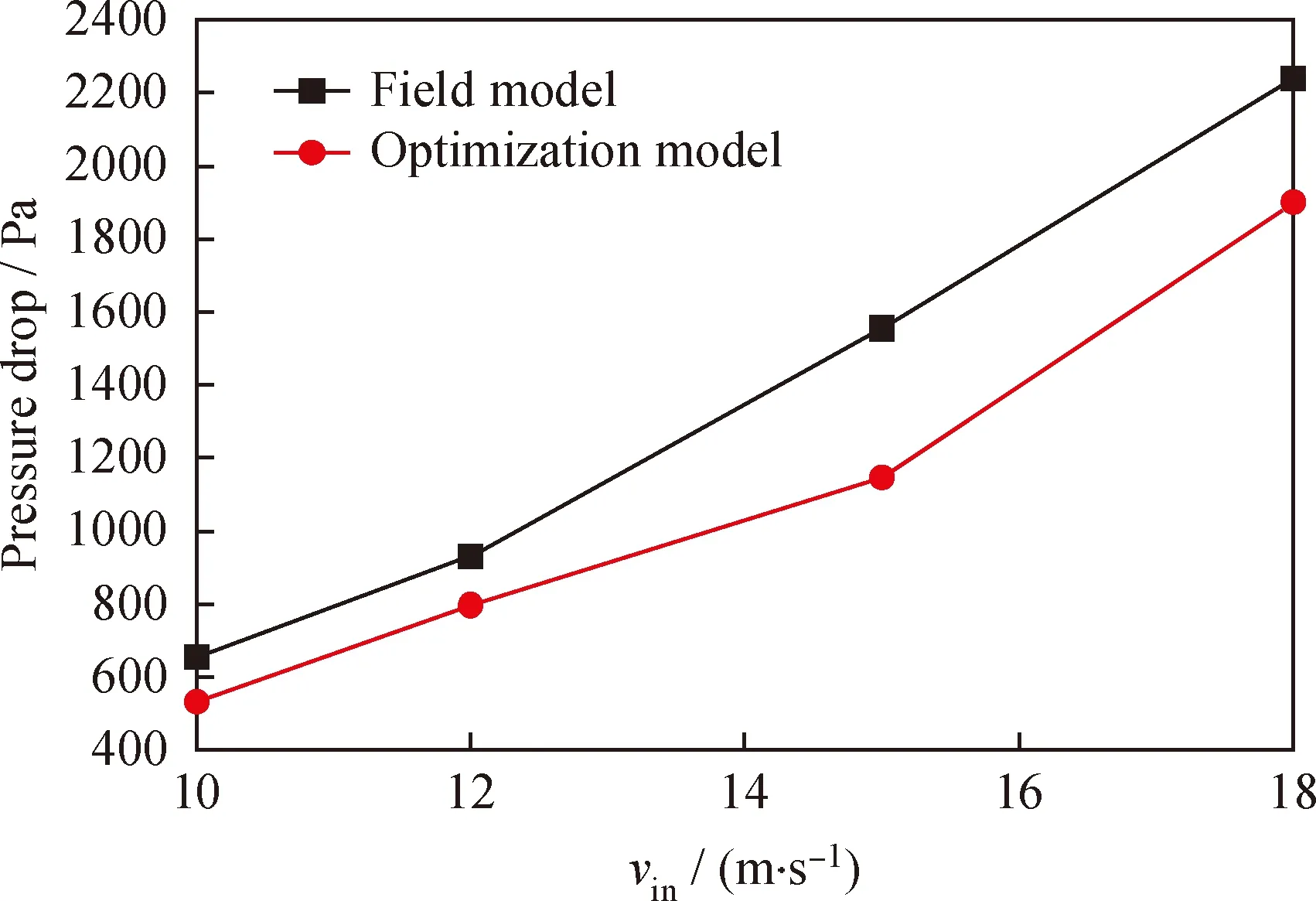
图10 催化裂化装置沉降器粗旋现场模型和优化模型压降分布Fig.10 Pressure drop distribution of the field model and theoptimization model of FCC settler separator

3.3 固相颗粒在现场模型和优化模型中的运行轨迹和分离效率

3.3.1 颗粒运动轨迹

本次模拟采用DPM模型。图11为催化裂化装置沉降器粗旋现场模型和优化模型颗粒运动轨迹图。由图11(a)看到，现场模型中粒径为1 μm、5 μm、9 μm的颗粒从进气口进入粗旋后随气流做螺旋运动，由于其粒径较小，螺旋运动半径较小，当颗粒运动到排气管附近时，很容易被短路流影响其运动轨迹，在向上运行的气流的夹带下进入排气管，进而直接排出粗旋，因而达不到分离的目的，降低了粗旋的分离效率。当颗粒粒径为13 μm时做螺旋运动的直径较大，一直做螺旋运动到达颗粒捕集口，从而达到分离的目的。

由图11(b)看到，与现场模型相比，优化模型中的颗粒在9 μm时就得到了捕集(概率大，说明分离效果增加)，并且随着粒径增大，颗粒更容易被分离。

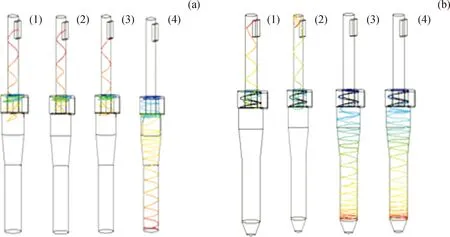
图11 催化裂化装置沉降器粗旋现场模型和优化模型颗粒运动轨迹Fig.11 Particle trajectories of the field model and the optimization model of FCC settler separatorvin=12 m/sd/μm: (1) 1; (2) 5; (3) 9; (4) 13(a) Field model; (b) Optimization model

3.3.2 分离效率

图12为现场模型和优化模型入口速度分别为12、15 m/s条件下不同粒径颗粒的分离效率。从图12 可以看出，该模型对粒径在5 μm以下的颗粒分离效率很差，低于50%；对粒径在20 μm以上的颗粒分离效率很高，达到90%以上，对25 μm左右颗粒可达到100%。这说明模型优化后对1 ～20 μm的分离效率提高明显，并且粒径越小，分离效率提高得越明显。

图13为入口速度对不同粒径的颗粒分离效率的影响。从图13可以看出，随着入口速度增大，现场模型和优化模型对颗粒的分离效率都逐渐增高，尤其是对粒径范围在5 ～20 μm的颗粒提高更加明显。

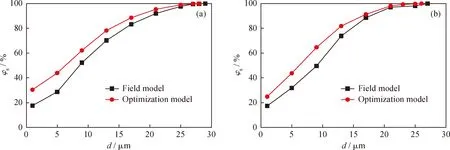
图12 不同进口速度(vin)下催化裂化装置沉降器粗旋现场模型和优化模型中颗粒分离效率(φs)随粒径(d)变化曲线Fig.12 Particle separation efficiency (φs) vs d of the field model andthe optimization model of FCC settler separator at different vinvin/(m·s-1): (a) 12; (b) 15

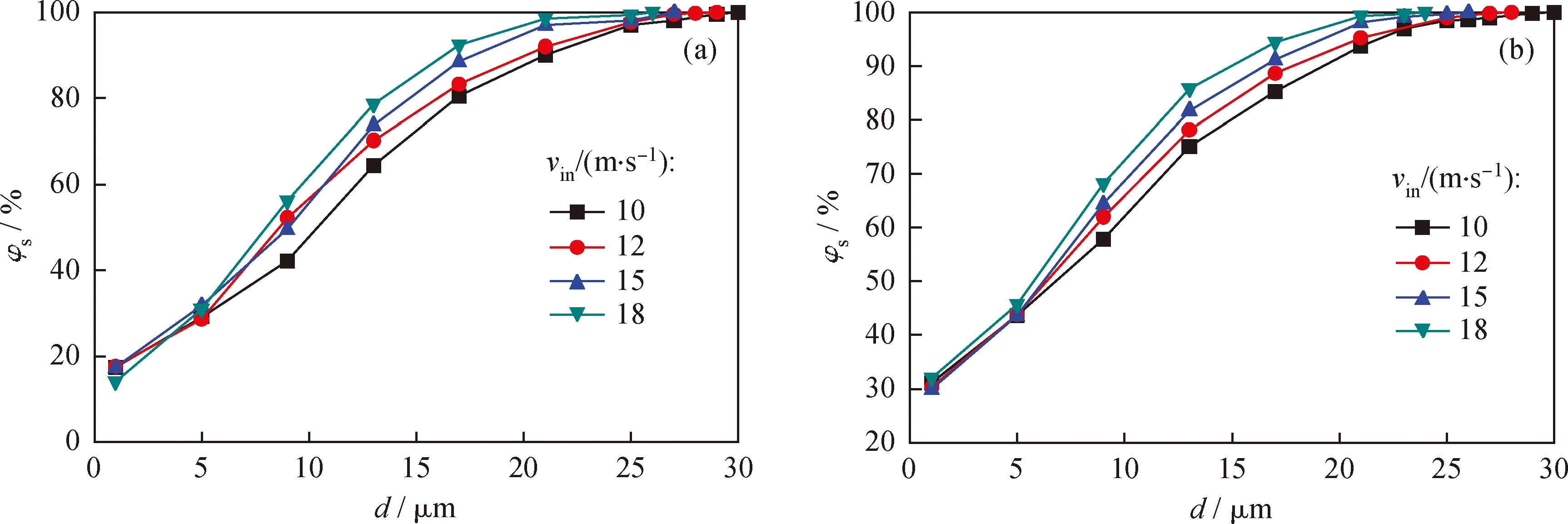
图13 入口速度(vin)对催化裂化装置沉降器粗旋现场模型和优化模型中不同粒径颗粒分离效率(φs)的影响Fig.13 Effects of inlet velocity (vin) on separation efficiency (φs) of different size particles for thefield model and the optimization model of FCC settler separator(a) Field model; (b) Optimization model

4 催化裂化装置沉降器粗旋模拟结果可靠性验证

由于旋风分离器流场复杂，没有适宜的测试方法来测量内部流场特性，因此通过测量分离效率来验证模拟结果可靠性[25-26]。冷模实验装置如图14所示，主要包括压缩机、旋风分离器、螺旋输送器、催化剂储料罐等。空气经压缩机从旋风分离器切向进口进入，催化剂颗粒经螺旋输送器从催化剂储料罐进入空气管线，经分离后，催化剂粉末进入催化剂储料罐重复使用，空气从旋风分离器顶部排出。实验过程中，分别测量切向进口和底流口处催化剂颗粒的质量m1、m2，则分离效率φe可由式(7)计算。

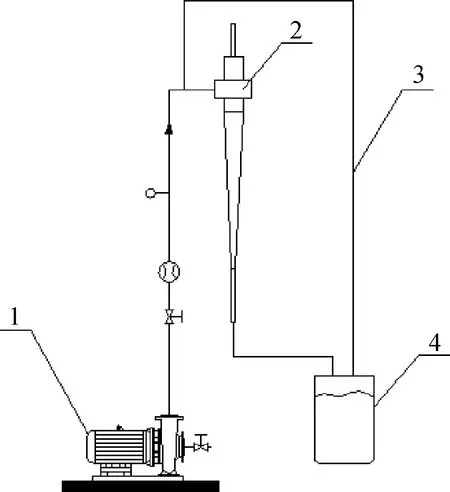
图14 催化裂化装置沉降器粗旋冷模实验装置结构示意图Fig.14 Schematic diagram of the experiment FCC settler separator1—Compressor; 2—Separator; 3—Screw conveyor;4—Particle storage tank

(7)

而模拟所得的分离效率φs，通过监测入口和底流口处催化剂颗粒质量流量Mi、Mo(kg/s)，按式(8)计算。

(8)

保持入口速度不变，实验和模拟所测的分离效率随催化剂颗粒的变化如图15所示。由图15可以看出，不同粒径的催化剂颗粒分离效率的模拟值与实验值比较吻合，由此可见模拟结果是可信的。

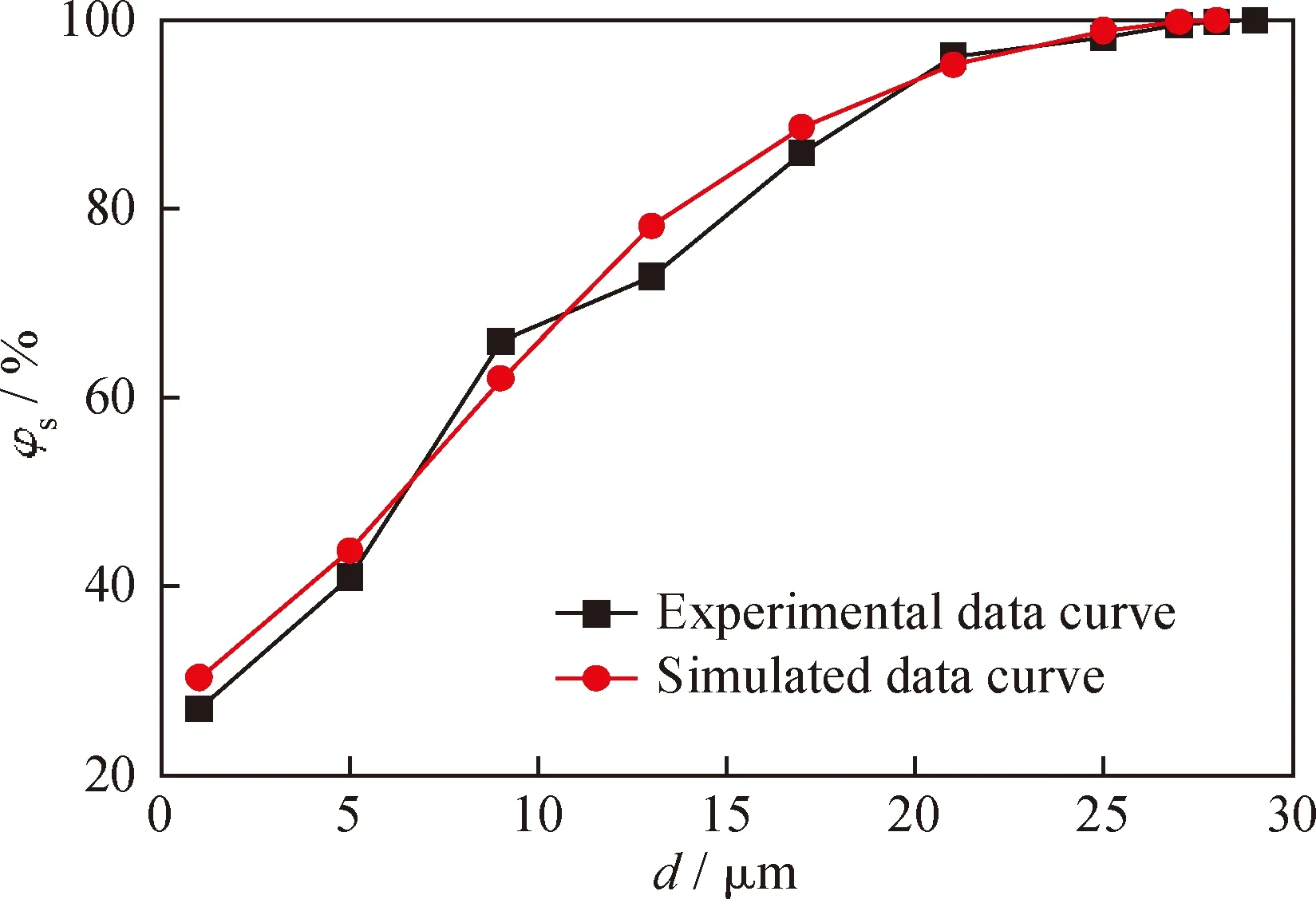
图15 催化裂化装置沉降器粗旋分离效率(φs)模拟值与实验值对比Fig.15 Comparison of simulated and experimental values ofseparation efficiency (φs) in the FCC settler separatorvin=15 m/s

此外，根据文献[18]，在旋风分离器入口段加装螺旋导流板能够提高对小颗粒的捕集效率，该结构已应用于某公司100 kt/a苯胺系统中，取得了良好的应用效果，进一步说明了本研究的合理性。

5 结 论

通过对催化裂化装置沉降器粗旋内流场模拟，得到以下结论：

(1)切向速度呈“驼峰”形分布；轴向速度呈“马鞍形”分布。切向速度数值最大，也是旋风分离器中起决定因素的速度分量。经过优化后，切向速度有较明显的提高，尤其是在气-固分离区域提高明显，这将有利于气-固两相的分离；轴向速度方面，优化后对旋转向下的“外旋流”影响不大，主要是对旋转向上的“内旋流”产生的作用，在轴中心区域，其轴向速度降低了1 m/s，由于“内旋流”在进入排气管时会发生紊流现象，因此，降低其轴向速度可减少紊流现象，从而减少能量的损耗。

(2)压力场呈轴对称分布，由于动压相比静压低4个数量级，所以总压分布基本与静压一致。通过对比，优化后模型压降较低。

(3)通过对颗粒分离效率的模拟计算得到，优化后提高了粒径在5～20 μm之间颗粒的分离效率。随着进口速度的增大，分离效率提高。

(4)增大入口速度可以提高旋风分离器的分离效率，但同时也会增大压降，因此需要综合考虑。