湍流乙烯扩散火焰中碳黑的数值模拟研究

伍祥瑞，毛军逵，贺振宗，梁 栋

（南京航空航天大学能源与动力学院，南京 210016）

碳黑颗粒（soot）作为常见的碳氢燃料燃烧产物，通常以分形团聚形态存在。碳黑颗粒的排放会危害人体健康，引发呼吸道感染、肺癌等疾病。同时，大气层中碳黑颗粒也会影响大气层的辐射传输，导致极端恶劣天气，如温室效应、酸雨等［1］。

碳黑颗粒具有很强的吸收散射特性。在典型的碳黑发光火焰中，尽管碳黑颗粒浓度很低，体积分数大多为10-6数量级，但其发射辐射却是CO2、H2O等气体的 2倍多［2］。Robert［3］在研究颗粒和气体辐射对富氧燃料燃烧的影响时指出，辐射换热是燃烧室中的主要传热方式，碳黑颗粒辐射传热作为主要的辐射源对整个燃烧室温度场分布的影响十分巨大，尤其在高温区域，碳黑颗粒会增强辐射换热，而在低温区域，碳黑颗粒作为吸收体能够使温度分布更加均匀。因此，准确模拟碳黑浓度和分布对辐射换热以及火焰温度的准确预估极为重要，对航空发动机燃烧室的优化设计以及减少碳黑的排放有着重要的指导意义。

碳黑颗粒的形成主要由以下4个步骤组成：前驱体形成、颗粒成核、颗粒表面生长和颗粒氧化［1］。目前，模拟碳黑颗粒生成模型主要分为3类：第1类是纯经验模型，利用实验数据的相关性预测碳黑大小，预测误差较大，通用性较差；第2类是详细模型，通过详细化学反应机理模拟燃烧生成碳黑过程中的所有重要组分和步骤，计算量巨大不适合工程应用；第3类是半经验模型，利用简单公式求解碳黑成核、表面生长和氧化的速率方程，根据实验数据确定模型常数，半经验模型兼顾了前2类模型的优势而得到广泛的应用［4］。

半经验模型的模型常数都是在一定的燃料和燃烧条件下得到的实验数据标定而来，例如著名的Moss-Brooks模型［5］的模型常数就是由层流甲烷火焰的实验数据标定得到。因此，把该模型用于其他燃料时就会带来一定的偏差，需要对模型常数进行修正。例如Moss JB通过对多个模型常数进行修正，把该模型应用到高压层流乙烯扩散燃烧［6］、煤油燃烧［7］、丙烯燃烧［8］等，得到更准确的模拟结果；Ng等［9-10］通过修正 Moss-Brooks模型中活化温度和氧化速率常数得到适合柴油机工况的碳黑预测模型；Pravin Rajeshirke［11］通过研究煤油燃烧中模型常数的影响，得到Moss-Brooks中碳黑成核速率常数Cα对碳黑的浓度影响最为关键的结论。可以看出，对Moss-Brooks模型常数的修正多针对于煤油等高阶碳氢燃料，而乙烯在基础实验和数值研究中都常常被用到，因此在Moss-Brooks模型中针对湍流乙烯扩散火焰对氧化模型进行选择和对碳黑模型常数进行修正有着重要意义。

本文为了准确地模拟湍流乙烯空气扩散火焰中碳黑的生成，通过比较不同的氧化模型、羟基计算模型来考虑氧化作用对碳黑分布的影响，得到合适的氧化模型组合，在Moss-Brooks模型及其扩展得到的Moss-Brooks-Hall模型［12-13］下分别研究不同的碳黑成核速率常数 Cα和 Cα，1、Cα，2对碳黑生成的影响，从而得到适合乙烯燃烧的模型组合以及碳黑成核速率常数。

1 数学模型

1.1 Moss-Brookes模型

Moss-Brookes两方程模型［5］即通过求解碳黑成核浓度和碳黑质量分数Ysoot的输运方程来得到碳黑的浓度分布：

式中：Ysoot表示碳黑质量分数；M表示碳黑质量浓度（kg／m3）；表示归一化的原子成核浓度N／ρNnorm（颗粒数 ×10-15／kg）；N表示碳黑颗粒数密度（颗粒数／m3）；Nnom＝1015；μt／σsoot为碳黑质量分数的扩散系数；μt／σnuc为碳黑原子成核的扩散系数。

式（1）中碳黑质量分数的源项为碳黑质量浓度的生成速率，可以分解为成核、表面增长和氧化等几个子步骤，如式（3）所示。式（2）中碳黑成核浓度源项为碳黑颗粒生成速率，由气态前驱成核速率和碳黑颗粒的聚集决定，如式（4）所示。

在式（3）和（4）中：Cα＝54 s-1为碳黑成核速率常数；Cβ＝1为聚集速率常数；Coxid为氧化速率缩放常数；Cy为表面生长系数；Cw，1、Cw，2为氧化系数；Mp＝144 kg／kmol为初始碳黑颗粒的质量；ρsoot＝1 800 kg／m3为碳黑质量密度；Xsgs为参与表面增长物质的摩尔分数，本文中选择乙炔作为碳黑表面增长物；Xprec为碳黑前驱的摩尔分数，本文中选择乙炔作为前驱。

Fenimore and Jones氧化模型［14］（下文简称 FJ模型）假设氧化速率由羟基OH控制，其中：氧化速率缩放系数Coxid＝1；碰撞率 ηcoll＝0.04。而在Lee［15］氧化模型中氧化剂包括了羟基OH和氧分子O2，氧化速率缩放系数 Coxid＝0.015，碰撞率ηcoll＝0.13。本文通过比较不同的氧化模型以及羟基的计算方式对碳黑分布的影响，选择适合乙烯燃烧的氧化模型组合。

其他未说明的参数皆为Moss-Brookes模型的原始参数，详情可参见文献［5］。从式（3）（4）中可以看出，由甲烷层流火焰的碳黑实验数据拟合而来的3个模型常数Cα、Cβ、Coxid中碳黑成核速率常数Cα对于碳黑的生成最为重要［11］，因为Cα直接决定了碳黑成核的成核速率，成核速率不仅在式（3）中影响碳黑质量浓度，还在式（4）中影响碳黑颗粒数密度。成核速率还与碳黑前驱体乙炔的量成正比，而在乙烯火焰中因为碳黑前驱乙炔的量比甲烷火焰中多，用Moss-Brookes模型中默认由甲烷火焰实验数据拟合来的模型常数会带来碳黑预测量的偏高，因此在本文中通过减小Cα来修正Moss-Brookes模型对乙烯燃烧生成碳黑的预测。

1.2 Moss-Brookes-Hall模型

Moss-Brookes-Hall模 型［12，13］是 在 Moss-Brookes的基础上为了考虑更高碳的碳氢燃料燃烧发展而来的，该模型的碳黑成核速率由两环和三环芳香烃（C10H7、C14H10）的生成速率所决定，如式（5）所示，模型其他部分与Moss-Brookes模型基本相同。

其中：成核速率常数 Cα，1＝127×108.88s-1；Cα，2＝178×109.5s-1；Tα，1＝4378 K；Tα，2＝6390 K是 Hall等基于层流甲烷火焰的实验数据标定得到的。由式（5）可以看出运用该模型的前提条件是燃烧机理中包括 H2、C2H2、C6H5、C6H6等组分。与 Moss-Brookes类似，本文通过减小成核速率常数 Cα，1、Cα，2来修正该模型对乙烯燃烧生成碳黑的模拟。

1.3 羟基计算模型

从式（3）可以看出，无论是Lee氧化模型还是FJ氧化模型都把羟基作为氧化剂，因此羟基的计算方式对碳黑的大小和分布很重要。羟基的计算模型分为瞬时型和平衡型2种，其中瞬时型Instantaneous模型即为燃烧模型燃烧得到的组分OH，通过PDF查表得来。平衡型Equilibrium通过氧原子与水分子的化学反应平衡计算得来，如式（6）所示［14］。

本文通过比较不同氧化模型和羟基计算模型对碳黑生成的影响，选择出适合乙烯燃烧的氧化模型组合。

2 模拟方法

2.1 研究对象

本文以德国航空航天中心K.P.Geigle等［16］的乙烯空气抬举扩散火焰实验为基准研究对象，研究氧化组合方式的影响和修正碳黑成核速率常数。物理模型如图1所示［17］，燃料喷嘴出口直径为2 mm，喷嘴外伴流空气直径为140 mm。本文模拟的燃烧工况下全局当量比为0.48，火焰可见高度约400 mm，实验数据见表1。本文计算域以喷嘴和伴流出口为边界，中心轴向为对称轴，轴向延伸600 mm，径向延伸100 mm。

以美国桑迪亚国家实验室Shaddix等［18-19］的湍流乙烯射流火焰为验证对象，对选择的氧化组合方式和修正的碳黑成核速率常数进行验证。该模型与基准模型不同的是在喷嘴和伴流中间为当量比1的乙烯值班火焰，实验数据见表2。

图1 基准物理模型示意图

表1 基准模型实验边界条件

表2 验证模型实验边界条件

喷嘴进口的边界条件通过模拟一个与喷嘴同样直径的充分发展的圆管，截取过该圆管圆心直径上的速度、湍动能和湍流耗散率分布得到。

伴流和计算域顶部以0.29 m／s的轴向速度作为速度进口的边界，对称中心设为轴，出口为压力出口。通过网格无关性验证选取网格数为39 240的网格，如图2所示。

图2 基准计算域网格

2.2 求解方法

本文采用k-epsilon湍流模型。由于标准的kepsilon模型预测射流的扩张率过大，因此把湍流模型常数C1-Epsilon由1.44修改为1.6［19］。本文应用部分预混燃烧模型，通过求解非绝热的稳态扩散火焰面模型并结合假定概率密度函数（PDF）来考虑湍流化学作用。化学反应机理采用米兰理工大学POLIMI详细化学反应机理［20］，包括84种组分和1 698步反应。辐射换热计算采用球谐函数模型（P1）求解辐射传输方程，其中考虑碳黑颗粒的辐射作用，用基于HITEMP2010光谱数据库拟合得来的最新灰气体加权和模型［21］（WSGG）计算碳黑颗粒和气体介质的辐射特性。

3 模拟结果及讨论

3.1 基准模型网格无关性验证

基准模型以非均匀的39 240个结构化网格为基准Mesh，在该套网格的基础上对其进行约4倍的加密，得到网格数为157 680的细网格4 Mesh。在关闭碳黑模型的条件下进行网格无关性验证，得到流场和温度分布。

图3展示了中心线上轴向速度和温度沿轴向的分布，可以看出在轴向方向上轴向速度和温度分布用2套网格得到结果几乎没有差别。

如图4所示，也可以得到在径向方向上的与轴向速度分布同样的结论，因此基准网格满足网格的独立性要求，在后面的模拟中以基准网格进行计算。图3中所预测的火焰后部温度偏高是因为没有加入碳黑模型，忽略了碳黑颗粒的辐射换热造成的。图4中可以看出，射流前段流场与实验值吻合得较好，能比较准确地预测径向方向上的轴向速度分布。随着轴向距离x的增加，预测的速度在中心轴处偏低，而扩张率偏高导致沿着径向方向延生时速度偏高。

图3 沿轴向的轴向速度分布（a）和温度分布（b）

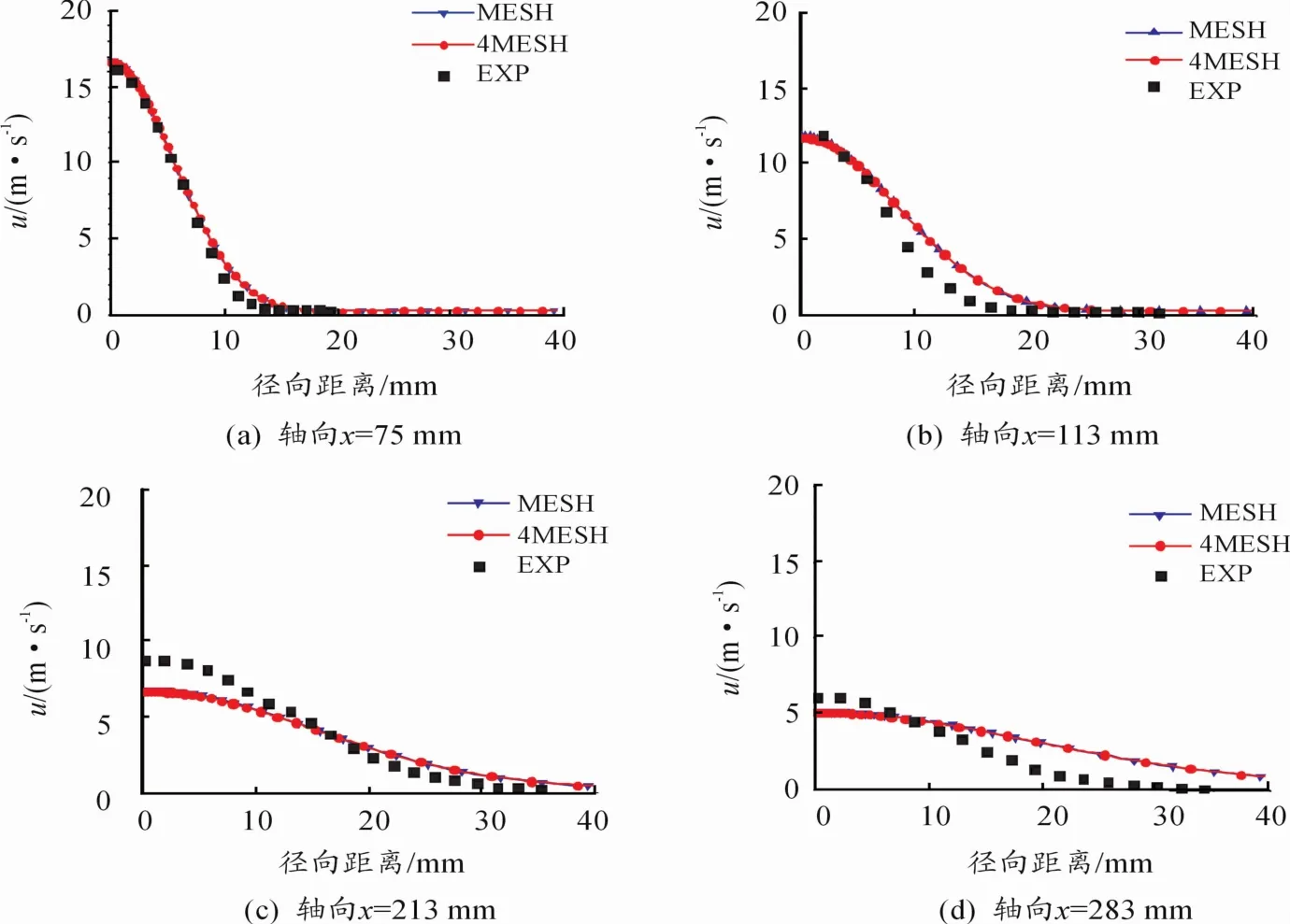
图4 径向方向上的轴向速度分布

3.2 Moss-brook模型选择

在本小节中基于Moss-Brooks碳黑模型，在不同的氧化模型和羟基计算模型中组合得到适合乙烯燃料的碳黑预测模型组合。从图5中可以看出：在Moss-Brooks模型下预测的碳黑体积分数整体偏大，在火焰尾部的碳黑浓度减少有限，这将会造成过量的辐射换热预测，从而使火焰尾部温度偏低。这是因为Moss-Brooks模型的默认模型常数是由层流甲烷燃烧的碳黑实验数据拟合而来，而甲烷燃烧生成乙炔需要先生成甲基再与自由基反应形成乙炔，因此生成的乙炔数量会比乙烯直接分解生成乙炔的量少，而碳黑数量的大小和分布与碳黑前驱乙炔的数量大小和分布直接相关，因此在甲烷燃烧下标定的碳黑成核速率等模型常数用在乙烯的燃烧上会造成碳黑体积分数的过大。

FJ氧化模型碳黑预测量低于Lee氧化模型，说明在乙烯火焰中FJ模型的氧化作用更强。而在FJ模型中氧化速率缩放系数为1，碰撞率为0.04，在Lee模型中分别为0.015和0.13，因此尽管Lee模型增加了氧分子作为氧化剂，但由于缩放系数过小使得氧化作用不如FJ模型，因此在FJ模型中因火焰后部的强氧化作用使得碳黑体积分数降低，更加接近实验值。

图5 Moss-Brooks模型下不同氧化模型组合的影响

在瞬时型和平衡型2种羟基的计算模型中，瞬时型预测的碳黑体积分数较低，说明瞬时型氧化较强，计算生成的羟基更多。因此，在只有羟基氧化的FJ-instantaneous模型下在尾部由于强氧化作用而造成碳黑分布较短，在距离射流出口350 mm后已无碳黑浓度。

而在Lee-instantaneous模型中因为氧化剂不仅有羟基，还包括了氧分子，氧化缩放系数减小为0.015，因此瞬时型羟基的增多对于碳黑的影响不如FJ模型那样强烈，碳黑体积分数相对平衡型只是有所降低，因此在碳黑浓度大小和分布上能较好地与实验值吻合。同样FJ-equilibrium模型因为较大的氧化速率缩放系数和较少的羟基生成使得该模型组合与实验值吻合得最好。

综上所述，在后续研究中选择使用 FJ-equilibrium、Lee-instantaneous两种氧化组合方式，分别研究在MB的碳黑生成中碳黑成核速率常数Cα和在MBH的碳黑生成中碳黑成核速率常数Cα，1、Cα，2对碳黑浓度大小和分布的影响，修正得到适合乙烯燃烧的碳黑成核速率常数，再在Shaddix等的湍流乙烯射流火焰上验证修正后的碳黑成核速率常数。

3． 3 碳黑成核速率常数Cα的修正

本节在MB模型中FJ-equilibrium、Lee-instantaneous两种氧化组合方式下通过把Cα从54缩小到27和5.4，研究碳黑体积分数的变化趋势和规律，得到适合乙烯燃烧的修正后的成核速率常数。同样在MBH模型中FJ-equilibrium氧化组合方式下分别把 Cα，1、Cα，2从 Cα，1＝127×108.88s-1，Cα，2＝178×109.5s-1修改为 Cα，1＝12.7×108.88s-1，Cα，2＝17.8×109.5s-1；Cα，1＝5×108.88s-1，Cα，2＝8×109.5s-1，到得MBH模型中适合乙烯燃烧的成核速率常数。

从图6～8中可以看出，随着碳黑成核速率常数Cα的减小，碳黑体积分数随之减少，同时温度升高，这与理论预测的规律相符。除此之外随着Cα的减小产生碳黑的峰值位置也沿着轴向向后移动，更加接近实验值在轴向300 mm处的峰值位置。如在图 8中，当 Cα，1＝127×108.88s-1，Cα，2＝178×109.5s-1缩小为 Cα，1＝5×108.88s-1，Cα，2＝8×109.5s-1之后，其碳黑的体积分数峰值从轴向240 mm处的2.2×10-6向后推移到275 mm处的0.64×10-6，向后移动了35 mm，从而更靠近实验值在轴向300 mm处0.54×10-6的峰值；同时轴向上的温度峰值从1 605 K升高到1 895 K，温度升高近300 K。这是由碳黑的强辐射特性造成的，碳黑颗粒浓度越大，其引起的辐射传热作用越强，使得火焰温度越低。因此，可以看出准确模拟碳黑浓度对温度的准确预估极其重要。

图6 MB-FJ-equilibrium模型组合下Cα常数修正

图7 MB-Lee-instantaneous模型组合下Cα常数修正

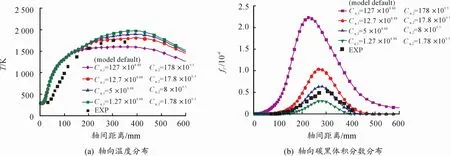
图 8 MBH-FJ-equilibrium模型组合下 Cα，1、Cα，2常数修正

在Moss-Brooks模型中，当Cα修正为5.4时，其预测的碳黑浓度大小和分布最接近实验值。在Moss-Brooks-Hall模 型 中，当 Cα，1、Cα，2修 正 为Cα，1＝5×108.88s-1，Cα，2＝8×109.5s-1时最接近实验值。

从图9中可以看出，在修正碳黑成核速率常数之后，MB-FJ-equilibrium模型组合预测的碳黑分布较窄，碳黑体积分数峰值比实验值前移约50 mm，偏离实验值最大，因此其温度分布也偏高。

MBH-FJ-equilibrium模型组合下的碳黑体积分数分布与实验值吻合得最好，但其预测的温度在火焰尾部偏高。而MB-Lee-instantaneous模型组合预测的碳黑体积分数在火焰尾部部分偏高，因此在火焰尾部由于较强的碳黑颗粒辐射作用使其温度相对于MBH-FJ-equilibrium模型组合有所降低，温度分布最接近实验值。

3.4 修正碳黑成核速率常数Cα的验证

本小节以美国桑迪亚国家实验室Shaddix等的湍流乙烯射流火焰为验证对象，对本文3.3小节选择的氧化组合方式和本文3.4小节修正的碳黑成核速率常数Cα进行验证。图10（a）（b）分别为以MB-FJ-equilibrium和MB-Lee-instantaneous碳黑模型下碳黑成核常数Cα为默认值及本文修正后的值对碳黑体积分数在射流轴线方向上分布的影响。可以看出，在默认的碳黑成核速率常数下2种模型对碳黑的预测都过高，最大值均为实验值的2倍多，当采用修正后Cα＝5.6的值时，与图9（b）中的结果相似。MB-FJ-equilibrium模型因为氧化作用更强所以预测的碳黑浓度稍偏小并偏向轴线前段，可见MB-Lee-instantaneous模型能准确地预测碳黑的浓度大小和分布。

本小节证明本文所选择的氧化组合方式以及修正的碳黑成核速率常数Cα能用于在不同的湍流乙烯火焰中预测碳黑的浓度大小和分布。

图10 碳黑成核速率常数Cα修正后的验证4结论

4 结论

本文以湍流乙烯扩散火焰为研究对象，研究Moss-Brookes和Moss-Brookes-Hall碳黑模型中不同氧化组合方式以及碳黑成核速率常数Cα对碳黑浓度和温度分布的影响。得出以下结论：

1）Moss-Brooks模型及其扩展模型 Moss-Brooks-Hall模型中包括了不同的氧化模型和氧化剂羟基的计算模型，在模拟不同的燃料时应有所选择。在模拟乙烯火焰的碳黑生成时，应选择FJ-equilibrium或者Lee-instantaneous的氧化方式。

2）常用的 Moss-Brooks模型和 Moss-Brooks-Hall模型的模型常数是由甲烷层流燃烧的实验数据拟合所得，该常数会高估乙烯火焰中的碳黑体积分数。采用修正的模型常数（Moss-Brooks模型Cα＝5.4，Moss-Brooks-Hall模型 Cα，1＝5×108.88s-1，Cα，2＝8×109.5s-1）能够比较准确地预测碳黑浓度分布。同时，发现采用修正碳黑成核速率常数后的MBH-FJ-equilibrium模型组合与MB-Leeinstantaneous模型组合能较准确地预测湍流乙烯火焰的碳黑浓度分布和温度分布。

3）碳黑颗粒的辐射特性极强，尽管其体积分数为10-6级，但其辐射传热特性对温度场分布有较大影响，例如碳黑分布的峰值体积分数增加1.56×10-6时将使火焰温度降低约300 K。因此，准确地预测碳黑浓度和分布对火焰传热机理以及温度场预估有着重要的意义。