精密钢球传动系统动力学建模与模态分析
2019-02-22安子军刘子强白晓鹏
张 悦, 安子军, 刘子强, 白晓鹏
(燕山大学 机械工程学院,河北 秦皇岛 066004)
精密钢球传动系统是一种利用钢球作为中介体来传递运动和力的新型传动机构,该机构具有无隙啮合、承载能力强、效率高、传动比范围广、噪声小等优点。同时本文采用十字钢球等速输出机构,该机构能够承受轴向载荷以及随机适应偏心距的要求。故精密钢球传动在机械手、伺服传动机构、机床分度机构等经常频繁往复工作的机构中具有良好的应用前景[1-3]。
关于精密钢球传动的研究,国内外学者已经取得一系列成果。文献[4]对摆线钢球传动的齿形形成和运动原理进行了阐述,并对齿形连续性及齿形参数选择进行了研究。文献[5]利用赫兹接触理论对摆线槽进行了接触强度计算,并进行了参数影响分析。文献[6]通过采用一种新的效率计算方法对摆线槽形进行优化,提出一种新型等速输出机构,并通过试验对输出机构的效率进行了测试。文献[7]建立了机构的力学模型,进行了力学性能分析,为新型减速器的定量设计提供了理论依据。张鹏等在忽略摆线槽曲率对啮合刚度的影响以及不计钢球质量和轴向预紧力作用的情况下,利用牛顿第二定律对摆线钢球行星传动系统建立了平移-扭转耦合动力学模型,文献[8]揭示了系统的固有特性,分析了系统结构参数对固有频率的影响;文献[9]利用多尺度法对系统进行了动力稳定性分析得到系统的稳定性条件,并通过摄动法计算出系统的稳态响应。杨荣刚等[10]在忽略啮合副啮合刚度为时变刚度的情况下,得到系统的固有频率和主振型,分析了结构参数对固有频率的影响,并通过试验验证了理论的正确性。系统在轴向预紧力的作用下,能够使啮合副实时四点接触。同时忽略钢球将会影响计算结果的精确性。因此,建立考虑啮合副四点接触、钢球运动和啮合副时变刚度等因素的动力学分析模型,对求解固有频率和主振型具有理论意义和学术价值。
综合考虑摆线槽曲率变化和法向力变化的影响,利用赫兹接触理论,通过求解由轴向力平衡方程和力矩平衡方程组成的非线性方程组,得到啮合副时变刚度。建立考虑啮合副四点接触、钢球运动和啮合副时变刚度等影响因素的精密钢球传动平移-扭转耦合动力学模型,推导系统动力学方程,通过自由振动特征方程求解系统各阶固有频率以及与其对应的主振型。
1 精密钢球传动系统结构介绍
精密钢球传动的结构,如图1(a)所示。等速啮合副滚动槽结构,如图1(b)所示。中心盘右侧加工有外摆线槽,行星盘左侧加工有内摆线槽,在内外摆线槽的交错区域放置减速钢球。行星盘右侧和浮动盘左侧加工有相同数量且相互平行的截面为等曲率半径的双圆弧滚动槽,在滚动槽中放置等速钢球组1。浮动盘右侧和输出盘左侧加工有相同数量且相互平行的截面为等曲率半径的双圆弧滚动槽,在滚动槽中放置等速钢球组2。浮动盘左右两侧的滚动槽相互垂直。机构运转时,输入轴带动行星盘转动,行星盘推动减速钢球运动,减速钢球在中心盘的限制作用下反推行星盘,使得行星盘以较低速度转动。行星盘通过等速钢球组1、浮动盘和等速钢球组2将转速等速传递给输出轴,实现等速输出。等速输出机构的等效机构为十字滑块机构。
2 啮合刚度分析
在间隙调节机构的轴向预紧力Fa的作用下,输出盘相对中心盘产生轴向微位移δa,各个啮合点处产生预变形量,使得啮合副实时四点接触(无隙啮合)。
中心盘、减速钢球和行星盘组成减速啮合副。
减速副在轴向预紧力的作用下,第i个减速钢球啮合点A,B,C,D承担的法向预紧力分别为FPAi,FPBi,FPCi,FPDi,法向预变形量分别为δPAi,δPBi,δPCi,δPDi。由行星盘相对于中心盘轴向微位移δ13与法向预变形量的几何关系可知
(1)
式中:β1为槽型角。
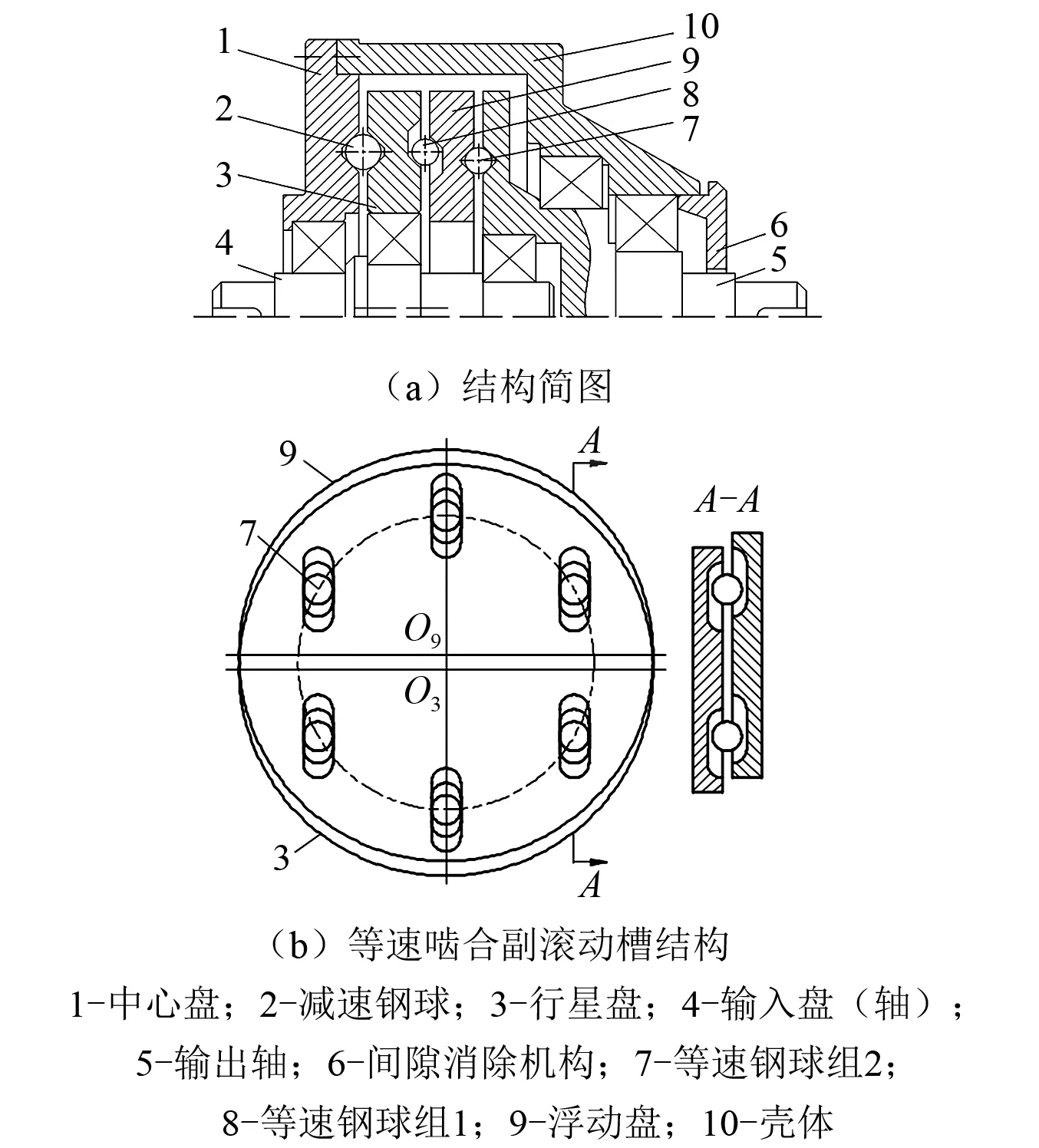
图1 精密钢球传动结构图Fig.1 Structure of precision ball transmission
输入轴顺时针转动时,行星盘受到阻力矩T1作用,因传力啮合点的变形量增加,非传力啮合点的变形量减小,使行星盘的转角产生滞后量α13,行星盘相对于中心盘的轴向微位移变化量Δδ13。
减速副在运转的过程中存在“换侧”现象,即传力侧与非传力侧相互转化。当0≤Φ2i<π时,即减速钢球位于坐标轴Y的左侧,啮合点B,D为传力啮合点,啮合点A,C为非传力啮合点;当π≤Φ2i<2π时,即减速钢球位于坐标轴Y的右侧,啮合点A,C为传力啮合点,啮合点B,D为非传力啮合点,如图3所示。则传力侧与非传力侧的变形协调方程分别为
(2)
式中:li为行星盘几何中心O3到啮合力方向PO2i的垂直距离,li=Z3e|sinΦ2i|;Z3为行星盘的齿数;e为输入轴偏心距一半;Φ2i为第i个减速钢球啮合法平面绕O2i点逆时针转过的角度。
由Hertz接触理论可知,啮合点法向力与变形量的非线性关系[11]为
(3)
其中,对于传力侧Gi=G1i
对于非传力侧Gi=G2i
由行星盘轴向力平衡和力矩平衡可得
(4)
式中:Φ4i为第i个减速钢球啮合法平面绕P点逆时针转过的角度。
因啮合点法向力与啮合点变形量为非线性关系,由文献[12]可知,实际啮合刚度为
kni=dF/dδ
(5)
式中:n分别取啮合点A,B,C,D;dF为啮合法向力的微小变化量;dδ为对应方向的微小变形量。
机构运转时,减速钢球的啮合点位置实时变化,使啮合点处的曲率和函数以及啮合点法向力实时发生变化。故求得的啮合副啮合刚度为时变刚度[13]。由于啮合刚度的表达式复杂,无显式表达式,故用MATLAB拟合工具箱中的傅里叶拟合可得,如图2所示。
(6)
式中:kmA为时变啮合刚度kAi的平均值。
行星盘、等速钢球组1和浮动盘组成等速啮合副1。浮动盘、等速钢球组2和输出盘组成等速啮合副2。等速机构中滚动槽截面采用等曲率半径的双圆弧结构,啮合点处的曲率和函数为定值。但作用力臂实时变化,使啮合法向力实时变化。因此,等速啮合副啮合刚度亦为时变刚度,如图2所示。
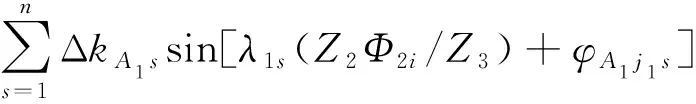
(7)
式中:kmA1为时变啮合刚度kA1j1的平均值。
同理可得啮合副的其余啮合点处啮合刚度。
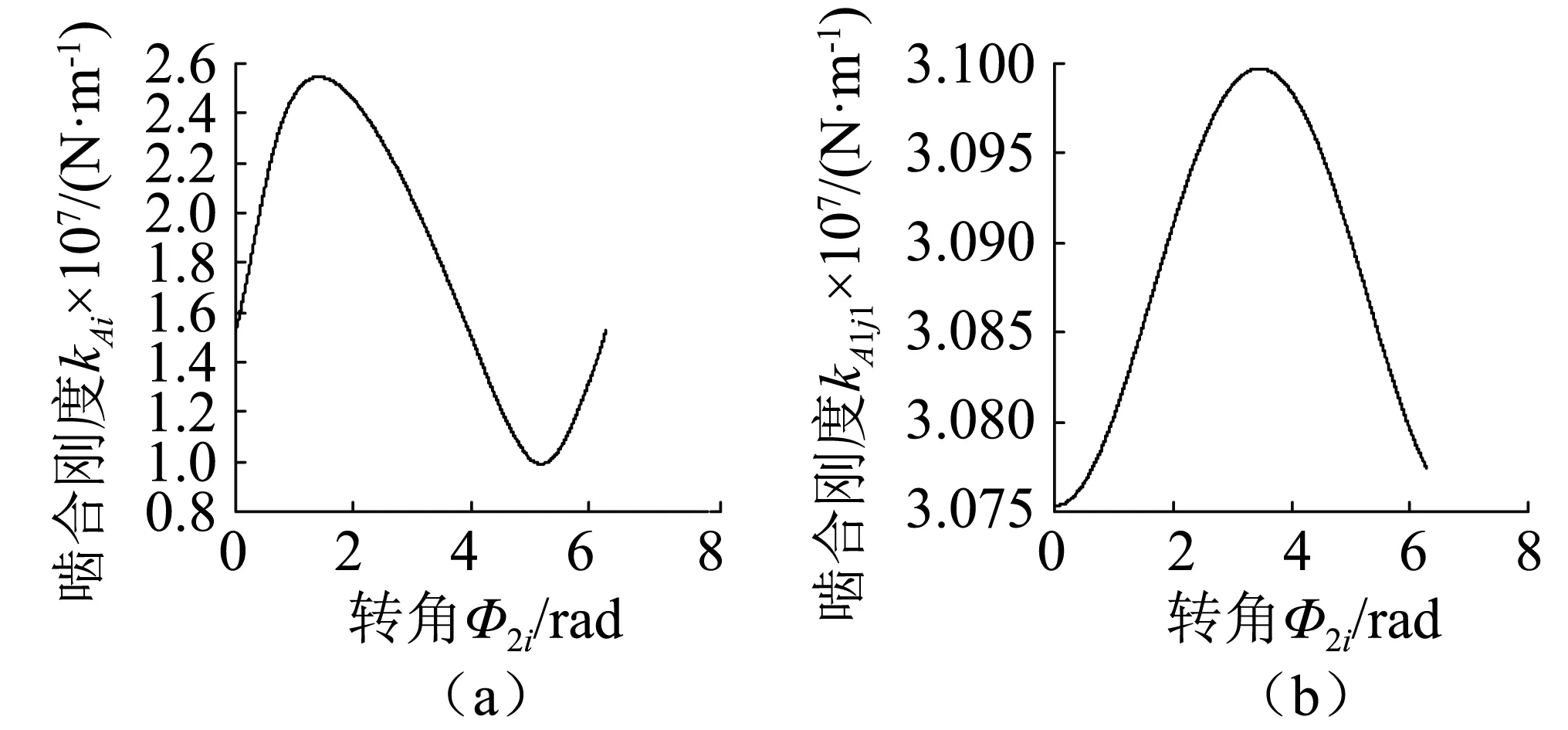
图2 时变啮合刚度kAi和kA1j1变化曲线Fig.2 Variation curve for time-varying mesh stiffness kAi and kA1j1
3 动力学模型建立
在动力学分析中作如下假设:①忽略传动系统运动过程中各构件的轴向振动;②采用集中参数模型,主要构件简化为刚体,轴承和各构件啮合处简化为弹簧;③忽略各处的阻尼和摩擦力。
如图3、图4所示,Φ1i为第i个减速钢球绕O2点转过的角度,Φ4i为第i个减速钢球啮合法平面绕P点转过的角度,Φ2i为第i个减速钢球啮合法平面绕O2i点逆时针转过的角度,Φ3为行星盘自转绕O3点转过的角度。O1XY为固定坐标系,O2X2Y2为与减速钢球系固连的坐标系,O2iX2iY2i为各减速钢球坐标系,i=1,2,...,Z2,其中Z2为减速钢球数,O3X3Y3为与行星盘固连的随动坐标系,O9x9y9为与浮动盘固连的坐标系,O9x9y9的两坐标轴与O3X3Y3的两坐标轴平行,O8j1x8j1y8j1为等速钢球组1中各钢球的坐标系,j1=1,2, ...,Z8,其中Z8为等速钢球数,O1x5y5为与输出轴固连的坐标系,O1x5y5的两坐标轴与O9x9y9的两坐标轴平行,O7j2x7j2y7j2为等速钢球组2中各钢球的坐标系,j2=1,2, ...,Z7,其中Z7为等速钢球数。xj,yj(j=0,1,21,22, ...,2Z2,3,81,82, ...,8Z8,9,71,72,...,7Z7,5)为各构件因振动产生的线位移,u0,u1,u3,u9,u5分别为各构件因振动产生的角位移(本文中的每个滚动槽放置一个钢球,滚动槽数与等速钢球数相等)。
3.1 各构件相对位移
由图3可知,中心盘、行星盘相对减速钢球位移沿啮合线方向的投影为
(8)

图3 减速啮合副动力学模型Fig.3 Dynamic model of reduction speed meshing pair
输入偏心轴相对行星盘的位移为
(9)
减速啮合副啮合点A,B,C,D处变形量分别为
(10)
由图4可知,行星盘、浮动盘和输出盘相对等速钢球位移沿啮合线方向的投影为
(11)

图4 等速啮合副动力学模型Fig.4 Dynamic model of constant speed meshing pair
式中:f(j1),f(j2)均为符号函数。
式中:lj1,l98j1,l97j2,lj2分别为几何中心O3,O8,O7,O5到啮合点法平面的距离;j1=j11,j12时,分别为位于X3轴上、下方的等速钢球组1中的钢球;j2=j21,j22时,分别为位于Y3轴右、左方的等速钢球组2中的钢球。
力臂lj1,l98j1,l97j2,lj2的表达式分别为
(12)
式中:α(j1)=|j1-[Z8/4]|·(2π/Z8);α(j2)=|j2-[Z7/4]| ·(2π/Z7);Rw为等速钢球分布圆半径;Z2为减速钢球个数; [Z8/4],[Z7/4]分别为对Z8/4,Z7/4取整。
等速啮合副1啮合点A1,B1,C1,D1变形量为
(13)
等速啮合副2啮合点A2,B2,C2,D2变形量为
(14)
3.2 各构件动力学微分方程
输入偏心轴的动力学微分方程为
(15)
式中:k01x,k01y分别为中心盘与输入轴x,y向的支承刚度;k03x,k03y分别为行星盘与输入轴x,y向的支承刚度;T1为输入轴转矩。
中心盘的动力学微分方程为
(16)
式中:k1x,k1y分别为中心盘x,y向的支承刚度;k1u为中心盘的扭转支承刚度。
行星盘的动力学微分方程为
(17)
等速钢球组1中第j1个钢球的动力学微分方程为
(kB1j1δB1j1-kA1j1δA1j1+kC1j1δC1j1-kD1j1δD1j1)=0
(18)
等速钢球组2中第j2个钢球的动力学微分方程为
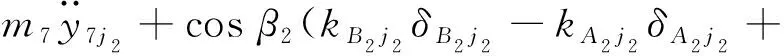
(19)
式中:β2为等速啮合副的压力角。
第i个减速钢球的动力学微分方程为
(20)
输出盘的动力学微分方程为
(21)
式中:T2为输出轴转矩;k5y为输出盘y向的支承刚度。
浮动盘的动力学微分方程为
(22)
3.3 系统动力学方程
联立式(15)~式(22),系统动力学方程的矩阵形式为
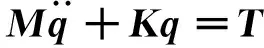
(23)
q=[x0y0u0x1y1u1x21y21...x2Z2y2Z2x3y3u3x81...
x8Z8x9y9u9y71...y7Z7y5u5]T
M=diag(m0,m0,J0,m1,m1,J1,m21,m21,...,m2Z2,m2Z2,
m3,m3,J3,m81,...,m8Z8,m9,m9,J9,m71,...,m7Z7,m5,J5)
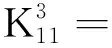
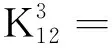

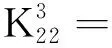
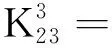
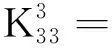
j=j11,j12(j11=1,2,...,Z8/2;j12=1,2,...,Z8/2)
j1=j11,j12(j11=1,2,...,Z8/2;j12=1,2,...,Z8/2)
j1=j11,j12(j11=1,2,...,Z8/2;j12=1,2,...,Z8/2)
j1=j11,j12(j11=1,2,...,Z8/2;j12=1,2,...,Z8/2)
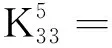
j1=j11,j12;j2=j21,j22
(j11=1,2,...,Z8/2;j12=1,2,...,Z8/2)
(j21=1,2,...,Z7/2;j22=1,2,...,Z7/2)
j2=j21,j22(j21=1,2,...,Z7/2;j22=1,2,...,Z7/2)
j2=j21,j22(j21=1,2,...,Z7/2;j22=1,2,...,Z7/2)
j2=j21,j22(j21=1,2,...,Z7/2;j22=1,2,...,Z7/2)
j2=j21,j22(j21=1,2,...,Z7/2;j22=1,2,...,Z7/2)
式中:T为外激励列阵,其中T1为输入轴转矩,T2为输出轴转矩;刚度矩阵K为14+2Z2+Z7+Z8维的对称阵;q为系统的广义坐标列阵;质量矩阵M为对角阵。
4 固有频率的求解
由式(23)可知,当系统外部激励列阵T=0时,无阻尼自由振动方程(矩阵形式)为
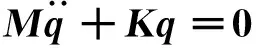
(24)
令式(24)的通解为q(t)=φhsin(ωht+θh),则可将式(24)转化为变特征值问题,其方程为:
(25)
式中:ωh为系统第h阶固有频率;φh为与其对应的振型矢量。
系统支承刚度取值如下:k03x=k03y=6×108N/m,k01x=k01y=k1x=k1y=k5y=5×108N/m,k1u= 5×106N·m/rad。
样机参数取值如下:Z1=9,Z2=10,Z3=11、短幅系数H=0.4,e=1.6 mm、滚圆半径r0=4 mm、减速钢球半径rq=2 mm,β1=π/4,Rw=35 mm、等速钢球半径rw=2 mm、滚动槽曲率半径rh=2rw,β2=π/6,Z7=6,Z8=6,E1=206 GPa,E2=206 GPa,μ1=0.3,μ2=0.3、轴向预紧力Fa=700 N、阻力矩T1=6 N·m。传动系统各构件的质量和转动惯量均由UG NX实体建模获得,见表1。
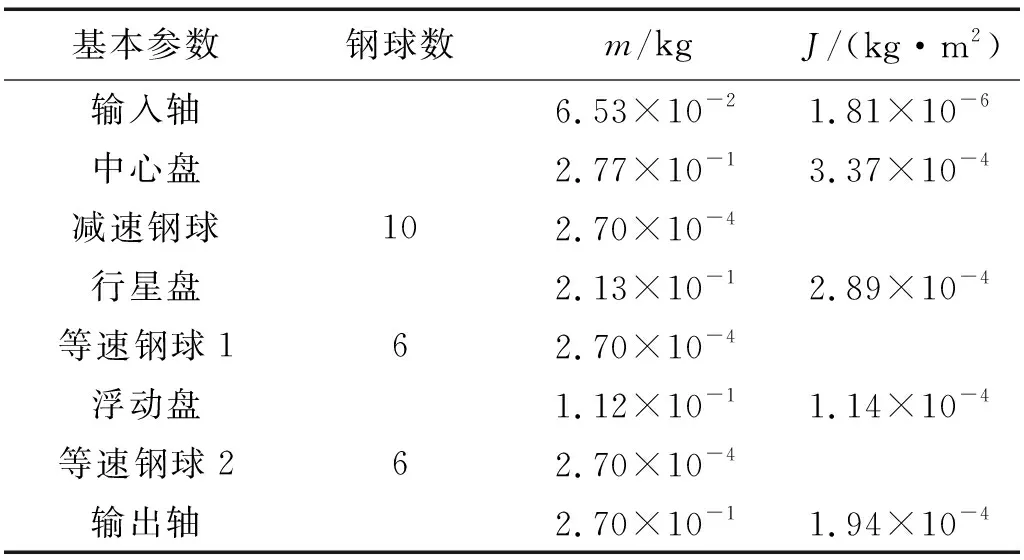
表1 传动系统质量和转动惯量
由系统动力学方程式(25)求得系统的固有频率和相应振型矢量。减速啮合副和等速啮合副的啮合刚度均为时变刚度,并且呈周期性变化,因此系统的固有频率和主振型[14]也是不断变化的。
如图5~图9所示,精密钢球传动系统46阶固有频率随转角Φ2i(0~2π)的变化规律,均呈周期性变化。

图5 传动系统的1~10阶固有频率周期变化曲线Fig.5 Periodic variation curves of 1—10 order natural frequencies of drive system
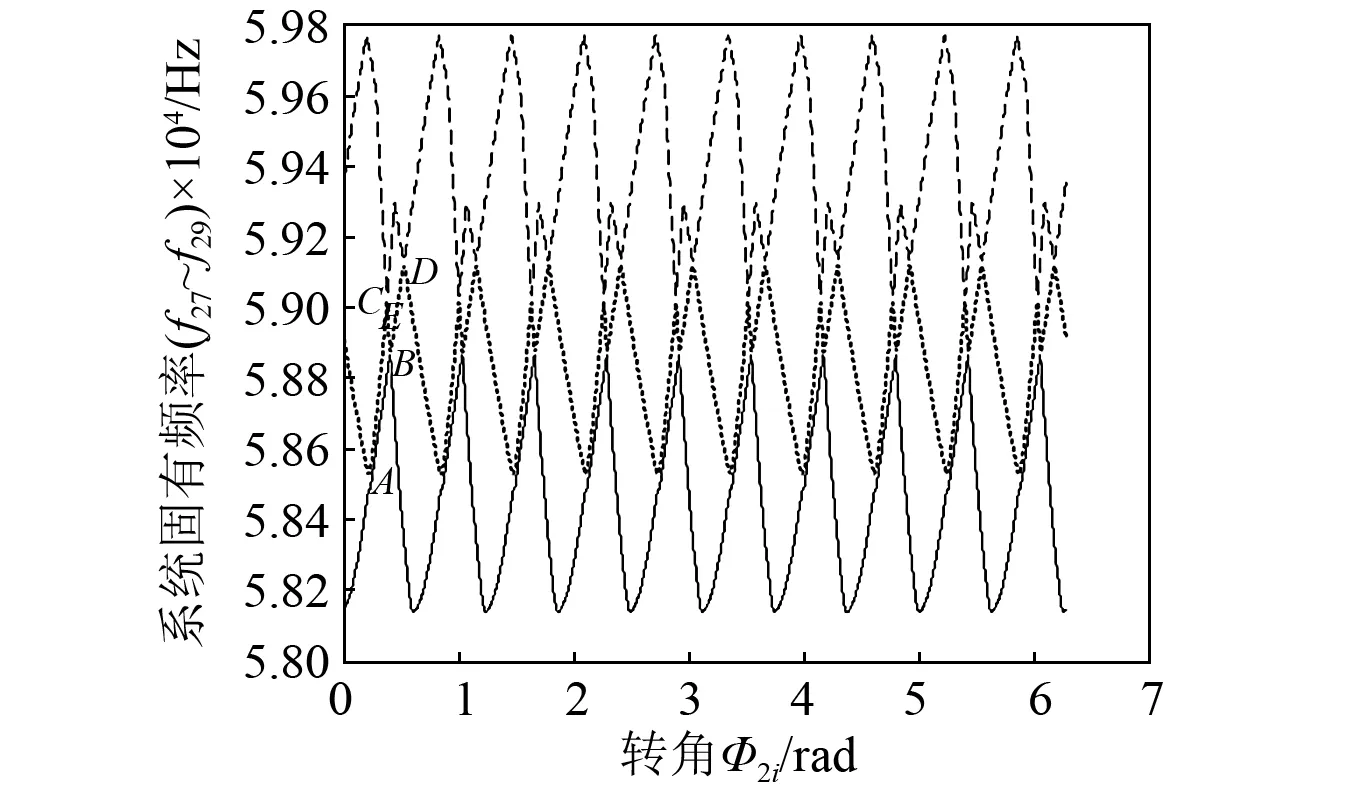
图6 传动系统的27~29阶固有频率周期变化曲线Fig.6 Periodic variation curves of 27—29 order natural frequencies of drive system

图7 传动系统的30~34阶固有频率周期变化曲线Fig.7 Periodic variation curves of 30—34 order natural frequencies of drive system
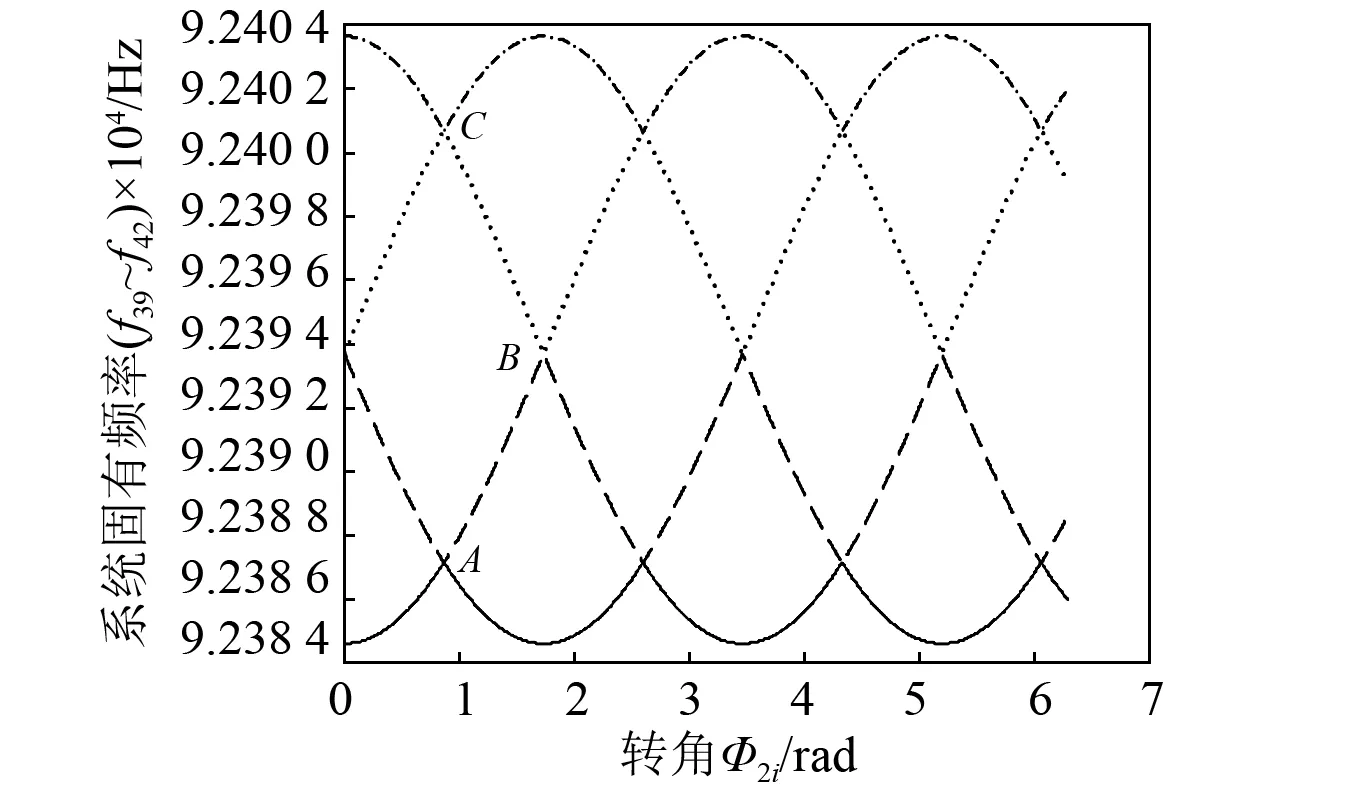
图8 传动系统的39~42阶固有频率周期变化曲线Fig.8 Periodic variation curves of 39—42 order natural frequencies of drive system
图5中,从下至上依次为系统的前10阶固有频率。前10阶固有频率轨迹变化的周期数与减速钢球数相等,均为10。低阶(1~10阶)固有频率对应的振动模式均为减速钢球平移振动,相邻的固有频率变化轨迹的斜率分别在点A,B,C,D,E,F,G,H,I附近急剧变化,看似相交实则未交,故前10阶相邻固有频率轨迹在点A,B,C,D,E,F,G,H,I处会发生模态跃迁。
图6中,自下而上分别为系统27~29阶固有频率。固有频率轨迹呈周期性变化,周期数等于减速钢球数。对应的振动模式均为减速钢球平移振动,固有频率轨迹斜率在点A,B,C,D附近急剧变化,故27阶与28阶固有频率会在点A,B处发生模态跃迁,28阶与29阶固有频率会在点C,D处发生模态跃迁。
图7中,自下而上分别为系统30~34阶固有频率。固有频率轨迹呈周期性变化,且周期数等于减速钢球数。对应的振动模式均为减速钢球平移振动,固有频率轨迹斜率在点A,B,C,D,E,F,G,H附近急剧变化,故30阶与31阶固有频率在点A,B处,31阶与32阶固有频率在点C,D,E处,32阶与33阶固有频率在点G,F处,33阶与34阶固有频率在点H处均会发生模态跃迁。
图8中,自下而上分别为系统39~42阶固有频率。固有频率轨迹呈周期性变化。固有频率轨迹斜率在点A,B,C附近急剧变化,且在点A,B,C处产生了固有频率“轨迹相交”现象。39阶和42阶固有频率为等速钢球组1直线振动模式,40阶和41阶固有频率为等速钢球组2直线振动模式。在“轨迹相交”位置A,C处,随着转角Φ2i的增加,会使等速钢球组1直线振动模式与等速钢球组2直线振动模式之间发生变化。
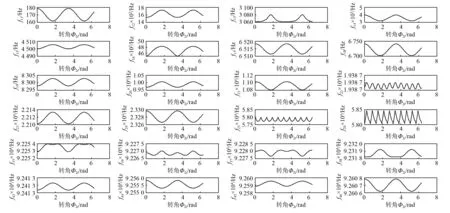
图9 传动系统其余固有频率周期变化曲线Fig.9 Periodic variation curves of other natural frequencies of drive system
5 结 论
本文考虑了啮合副四点接触、钢球及啮合副时变刚度等影响因素,通过对精密钢球传动系统平移-扭转耦合动力学模型的研究,得到如下结论:
(1) 考虑摆线槽曲率变化和啮合法向力变化对啮合刚度的影响,通过基于Hertz接触理论的精密钢球传动啮合副时变刚度计算方法,求得传动系统的时变啮合刚度呈周期性变化。
(2)应用系统平移-扭转耦合动力学模型,求解的系统各阶固有频率均呈周期性变化,低阶(1~10阶)、中高阶(25~34阶)固有频率变化的周期数与减速钢球数相等,在低阶(1~10阶)、中高阶(27~29阶)和(30~34阶)的各自固有频率轨迹接近处发生模态跃迁。
(3)在高阶(39~42阶)固有频率对应的振型中,随着转角的增加,在固有频率轨迹相交处,等速钢球组1直线振动模式与等速钢球组2直线振动模式之间会发生变化。
