教学设计应追求教材知识结构与学生认知水平的和谐统一
2019-02-21
安徽省合肥市教育科学研究院 (邮编:230071)
笔者是合肥市中学数学教研员,从自己大量的听课和各种推送赛课的过程中,深感影响课堂教学成败的因素很多,但最主要和最直接的因素是“教学设计”的合理性.2018年10月份安徽省数学会在合肥市举办了全省高中数学骨干教师课堂教学展示活动,本人有幸参与了点评.在欣赏安徽省骨干教师高素质的同时,就其中一节课教学内容,谈谈怎样设计更合理?因为教材是课程标准的具体体现,又是教师教学设计的依据,所以本文就人教A版教材必修2中第二章第三节第一小节《直线与平面垂直的判定》(第一课时)的教学内容,谈谈如何尽可能达到教材知识结构和学生认知水平的和谐统一.
1 教材呈现
1.1 课时内容
教材从给出现实生活中的旗杆与地面,大桥的桥柱与水面的位置关系出发,观察在阳光下旗杆与它在地面上的影子,感悟旗杆AB所在的直线与地面内任意一条直线垂直;从而得出直线与平面垂直的定义;再通过折纸探究,得出直线与平面垂直的判定定理;最后,讲解一条直线与平面垂直的判定定理的例题.
1.2 前后联系
在学习此节课以前,教材安排了:2.1 空间点、直线、平面之间的位置关系;直线与平面平行的判定及其性质.此节课以后,教材安排了:2.3.2 平面与平面垂直的判定;2.3.3 直线与平面垂直的性质;2.3.4 平面与平面垂直的性质.
与此节课有密切联系的内容,前面已学:直线与平面的位置关系;后续学习:直线与平面所成的角;平面与平面垂直的判定.
2 学生认知
按照安徽省大部分地市进行教学的顺序是高一学习必修1、4、5、3,高二学习必修2 及选修内容.因此,此节课是高二学生学习的内容,学生对知识的理解力和统摄力有了较大的提高.与此节课有紧密联系的是:在知识层面上,学生已经具备,初中学习了:在同一平面内两直线垂直的判定;高中学习了:空间中直线与平面的位置关系;空间中两直线垂直的判定.在认知上,具备了直线与平面平行的判定的研究基础.
3 设计思考
教材的知识结构,让学生“观察在阳光下旗杆与它在地面上的影子,感悟旗杆所在的直线与地面内任意一条直线垂直”,从而得出直线与平面垂直的定义.其实,由上面学生认知可知,直线与平面的位置关系是用直线与平面的公共点来定义的,且与此节课紧密联系的“直线与平面平行的定义”的得出是直接给出的,学生也极易接受.而学生学习直线与平面垂直的定义前,学生对垂直的概念学生习得的只有:直线与直线垂直,对直线与平面垂直只是“感觉”,没有对直线与平面整体垂直的认知基础,教材也只是为了定义“强加”给学生的“旗杆所在的直线与地面内任意一条直线垂直”.因此,这一节课教材的知识结构与学生的认知水平及认知结构不一致,教学中一定存在教学不自然或教师“强推”的现象.
对“直线与平面垂直”的判定定理的得出过程,类比“直线与平面平行”的得出是困难的.因为“直线与平面没有公共点”是“直线与平面平行”的定义,把“直线与平面没有公共点”转化为“平面外直线与平面内的直线无公共点”是寻找“线面平行”的充分条件.由于平面外直线与平面内直线的位置关系有:平行或异面.两直线异面难以判定,而两直线平行易于判定,因为两直线平行,则此两直线是共面的,所以学生判定的方法很多.因而,把“直线与平面没有公共点”的问题转化为“过面内所有点都有直线与已知直线平行”的问题,再将面内过所有点的平行直线减少至一条,由于线面平行同时把线面相交的情况加以否定,这样就得到直线与平面平行的判定.而“直线与平面垂直”的定义是“直线与平面内任意一条直线垂直”,即直线外一条直线与平面内所有直线垂直.显然,总体思维上难以类比,但怎么让面内无数且无序的直线条数减少的思维是一致的.而面内直线减少至直线有“两条”且“相交”,在减少面内直线的过程中,比前者少了“去异面直线”的过程,好在直线与面内“一条”直线垂直是不能判断线面垂直,只要通过学生“直观操作”就可以明确,因而两直线“相交”是得出判定定理之难点.
4 具体设计
4.1 引入
(1)空间中直线与平面的位置关系有哪些?
(2)“直线在平面外”中,“直线与平面平行”是怎样由定义得出判定的?
(3)我们已经学习了线面平行的定义,判定和性质,而“直线在平面外”中,还有一类位置关系是什么?请同学们在现实生活中举出与这一位置关系类似的情景?
设计意图问题(1):从与此节内容紧密联系的“直线与平面的位置关系”出发,从总体上把握位置关系的知识结构;问题(2):直线在平面外的位置关系中,已经研究了直线与平面平行位置关系的判定和性质,与此节课紧密联系的是:直线与平面平行判定的探究和思考过程,以期学生类比得出研究直线与平面垂直的思路.问题(3):已经学习了直线和平面有二(或三)种位置关系,已经掌握了直线和平面平行的定义,判定和性质,还有一种位置关系:直线与平面相交.让学生在认知结构上产生认知的需求,这时引导学生回到现实生活中,直观感悟直线与平面相交的现实情境,估计大部分学生都会举出“直线与平面垂直”的生活情境,少数学生举出“直线与平面斜交”的情境,因为生活中前者常见.直线与平面斜交的情况,过于一般,研究价值不大.因而重点研究“直线与平面垂直”的特殊情况.学生很容易想到:天安门广场和操场上立一面五星红旗,将旗杆抽象成一条直线,地面抽象成一个平面,“怎样检验旗杆与地面是不是垂直”.这个问题就是“如何判定直线与平面是否垂直”的问题,也就是今天我们要研究的课题.
4.2 新知
4.2.1 线面垂直的定义
(1)天安门广场和操场上立的一面五星红旗,将旗杆抽象成一条直线,地面抽象成一个平面,大家想象一下,这种直线与平面的位置关系你认为取一个什么名字合适?
(2)既然大家都认为“垂直”合适,那么大家能不能讲讲道理呢?
(3)同学们回答的都有道理,那么面内有很多直线,都与已知直线垂直吗?怎么理解?
设计意图问题(1)由于学生对空间中线线的位置关系比较熟悉,而线与线相交的平面问题更清楚,学生类比平面中线线的位置关系,通过类比不难得出这种特殊位置关系是直线与平面“垂直”;问题(2)让学生展开想象的翅膀,感知定义名称与内涵的合理性.学生可能有以下想法:如果把平面看成一条线,就是两条直线互相垂直,否则“旗杆”就是“歪”的;由于学生在学习线面平行的判定过程中,寻找面内直线与已知直线平行的启发,线面垂直的定义,是面内直线与已知直线垂直所致.问题(3)不能让学生操作发现或演示“旗杆与旗杆影的垂直”,得出定义.其一,后面判定的得出有:操作确认的过程;其二,逻辑上有“循环论证”之嫌;其三,学生认知的基础只有两直线的共面垂直和异面垂直的基础.因此,把线面垂直的问题转化为线线垂直的问题,符合学生认知的水平.建议用下面方法,在黑板上画出或ppt演示下面图形:
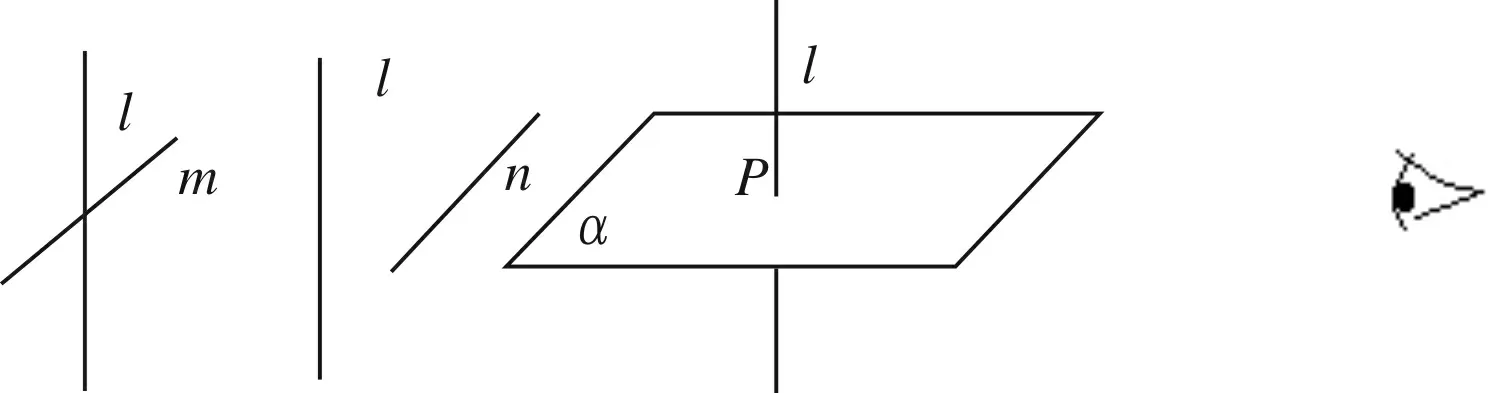
图1图2图3眼
图1是两直线共面垂直,图2两直线异面垂直,“旗杆与地面”的位置关系如图3所示,假设直线m//n,m、n和表示眼睛的点在平面α内,只不过图形表示的时候是分开表示的.若你站在足够远的地方从右向左分别看图1、图2,并在表示平面α的平行四边形的外,看图3,你看到的图形是什么?(都是两条互相垂直的共面直线).再将直线m、n平移至平面α内,且点P∈m∩l,P∉n,这时图3中平面α内的直线m、n与直线l有什么样的位置关系?如下图4所示:

图4
你能够进一步得出什么结论?(平面内所有与直线m平行的直线都与直线l垂直,即与直线m平行的直线“铺满”平面α,都与直线l垂直).平面内还有其他方向的直线与直线l有什么位置关系,怎么“看”呢?(移动“眼”到恰当的位置,同上,可以“看”其他方向的直线与直线l也垂直)你又得出什么结论呢?(平面α内任意一条直线都与直线l垂直).从而得出直线与平面垂直的定义.
定义如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作:l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做垂足.
4.2.2 线面垂直的判定
(1)根据定义判定直线与平面垂直,需要判定直线与平面内“任何一条直线”即“所有直线”都垂直,这种判定方法甚至是无法实现的,那么,我们能否类比线面平行的判定定理得出的过程,思考一下由“线面垂直定义”到“线面垂直判定”的研究思路或方法?
(2)大家一致认为把面内的直线条数减少到有限条,是最佳选择,那么平面内的直线有无数条,怎么减少呢?由定义前面的感知过程可知,同一方向的直线都垂直,也就是说,同一方向只取一条线,那么取哪条直线更直观?如:图4中取哪条直线?(取与直线l垂直的直线m,且P∈m∩l)
(3)这样平面α中的直线已经减少到过P点的不同方向的直线,但仍有无数条.那么不同方向的直线,仍有无数条,又怎么再减少直线条数呢?如果不能再减少,我们能不能反向思考一下,从这些不同方向的直线中取一条直线开始尝试操作,然后依次增加一条直线,直到能够判定线面垂直为止.那么,我们从先取一条直线与直线l垂直开始,请同学们思考或把课桌面看成一个平面,把手中的笔看成一条直线,操作一下.
(4)既然面内一条直线不行,那么过点P再增加面内一条直线呢?我来做一个操作试验:
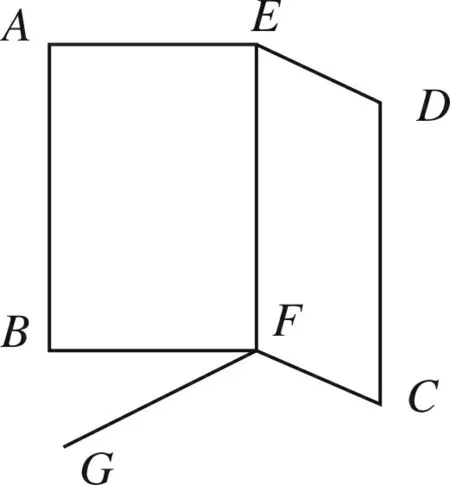
图5

图6
请同学们拿出准备好的一块矩形纸片,如图所示,过矩形两对边上分别取两边的中点E、F,过E、F两点的直线折叠,得到折痕EF,易知EF⊥BC,即EF⊥FB,EF⊥FC.沿着折痕EF翻折,使得纸片竖起放置在桌面上(BF、FC与桌面接触),如下图5所示.观察并思考:①在桌面上放一张白纸,放在矩形折纸的下面,过点F任意画一条直线FG,折痕所在的直线EF与直线FG垂直吗?(如图6)②请大家把书沿着书脊打开,不要展平,站立放置,即封面与封底两面如图5放置,看看其他页码的长方形页面与桌面接触的边与桌面是否完全吻合?说明什么?③根据定义,折痕EF所在的直线与桌面所在的平面垂直吗?
(5)你能够准确说出直线与平面垂直的判定方法吗?“两条相交直线”改为“两条平行直线”是否可以?是否可以增加至三条直线呢?
设计意图问题(1)回顾由线面平行的定义到线面平行判定的探究过程,思考由线面垂直的定义到线面垂直判定的探究过程,看看有没有可以借鉴的思考过程和方法,通过比较,提取对线面垂直判定有作用的“减少面内直线的条数”是合适的思考问题的方法;问题(2)由定义的感知,学生已经知道,同一方向的直线,只要一条垂直就可以了,这样减少了许多同方向的直线.那么同一方向取那一条好呢?因为学生最先学习的是共面相交,当然,直线m是最好的选择.这也为判定定理中的“面内两直线相交”打下伏笔;问题(3)由同一方向的直线,在平面内取与直线l相交的直线,那么过交点F的直线仍有无数条.继续减少直线条数已经没办法完成,让学生反向思维,从最少的一条直线出发,逐步增加直线条数,直线符合为止.先让学生操作,容易判定面内一条直线与直线l垂直是不行的;问题(4)是让学生“操作确认”判定定理的过程.先在确定面内两条相交线BF和FC,再让学生过点F画一直线,度量或利用三角板的直角判定所画直线是否与直线EF垂直,为了进一步判定与面内不同方向的直线垂直,让学生利用课本“直立”操作,观察其他页面的矩形的下面的一边是否在桌面内,学生得出不同方向的许多直线都与直线EF垂直,从而初步得出判定定理;问题(5)让学生明确问题(4)得到的方法合理后,为了加深对“两线相交”的理解和记忆,设计“两线平行”是否可以,也是对学习定义前“平行直线”只要一条垂直,其他直线一定垂直,所以平行直线条数再多也“没用”.同时,提问是否可以再加一条直线的问题,旨在让学生体会这种方法的简洁性和严谨性.
直线与平面垂直的判定定理

如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
图形语言表示:
符号语言表示:
2)放眼全球,重点选择。在埃克森美孚公司的七大油气战略区中,北美、南美、大洋洲是核心战略区,其次是欧洲和非洲,而亚洲及中东并不具有重要位置。中东以资源丰富且优质著称,埃克森美孚并没有太多涉足,仅进入卡塔尔、阿联酋、伊拉克等少数几个国家,也不占据主导地位。亚洲也是诸多国际石油公司早期进入并视为核心的战略区,埃克森美孚除了在哈萨克斯坦与雪佛龙、壳牌等大石油公司联合作业参股田齐兹、卡沙甘等少数几个大项目外,只进入印尼、马来西亚等少数国家,存在感不强。埃克森美孚非常看好俄罗斯北极地区,但随着美国对俄罗斯实施能源制裁,埃克森美孚不得不撤出了其在俄罗斯北极庞大的勘探项目。
a⊂α,b⊂α,a∩b=P,l⊥α,l⊥b⟹l⊥α.
4.3 应用
(1)前面多次学习到“一组平行直线”在不考虑位置不同的情况下,可以看作“一条直线”或“取其中的一条直线”.
我们在“2.2.3直线与平面平行的性质”中学习了例2:平面外的两条平行线,一条平行于平面,则另一条直线也和这个平面平行.
a∥α,b⊄α,a∥b⟹b∥α.
请大家思考一下,在直线与平面垂直中是否有类似的命题?(两条平行线,一条垂直于平面,则另一条直线也和这个平面垂直.)此命题是否正确?
设计意图通过此问,培养学生类比思维的习惯,并让学生形成合理而且完善的认知结构.同时,进一步加深:一组平行线在只考虑方向的情况下,可以只考虑其中的一条直线即可.也为下面例题的出现进行合理的过渡,并为例题的解决打下基础.
(2)例题
证明
方法一:由a⊥α,得:a垂直于α内所有直线,
又因为a//b,所有b垂直于α内所有直线
所以b⊥α.

方法二:在平面α内作两条相交直线m、n,
因为直线a⊥α,
根据直线与平面垂直的定义知:a⊥m,a⊥n.
又因为a//b,所以b⊥m,b⊥n,
又因为m⊂α,n⊂α,m、n是两条相交直线,所以b⊥α.
设计意图让学生初步体会:运用直线与平面垂直的定义和判定定理解决问题的思维方式,掌握应用线面垂直判定定理的条件与书写格式.
4.4 结课
(1)本节课你学会了哪些知识?
(2)定义到判定定理是怎样得到的?
(3)判定“直线与平面垂直的方法”有两个(定义法和判定定理法),判定定理法要注意什么?(“面内”、“两条相交直线”).
设计意图总结本节课的两个知识点(线面垂直的定义和判定)和知识发生发展的思维过程,重组学生的认识结构并使得新认知结构具有开放性.
其上,是对多次进行赛课内容:《直线与平面垂直的判定》,进行的个人设计,仅供大家参考.目的是让各位同仁明白:我们应该花大气力整合和改造教材中的知识,添加自己的处理内容,形成合理的知识结构,使得课堂教学的教学设计契合学生的认知水平.这样的教学设计,加上教师课堂教学中合理而机智的引导,才能够最大化地发挥学生潜能,使得学生“迷”上数学,这才是我们孜孜以求的“境界”.
