基于SolidWorks和ANSYS的液压支架顶梁疲劳可靠性分析

2019-02-19宋宇宁徐晓辰

煤炭工程 2019年1期

宋宇宁，徐晓辰

(营口理工学院，辽宁营口 115014)

液压支架是井下安全开采作业的关键设备，其结构组成主要包括：顶梁、前后连杆、掩护梁、底座以及用来控制结构件动作的液压系统构成。它承担着支撑综采面顶板，保证井下工人作业安全的任务，它的出现被认为是近代采煤行业的重要突破。液压支架顶梁与顶板直接接触，主要起承载支撑作用，是液压支架最容易损坏的结构，也是维修率最高的结构，其可靠性是影响液压支架整机可靠性的主要因素[1]。

近年来，我国对液压支架可靠性的研究日趋成熟，国内外相关学者在液压支架可靠性设计和评估方面做了许多研究，例如，陈静[2]利用可靠性优化设计理论及有限元的数值计算方法，对液压支架箱型结构进行了建模分析，实现了强度和结构的优化以及可靠性的提高；刘长友等[3]通过对兖州矿区多个放顶煤工作面放煤前、后液压支架后立柱工作阻力的跟班观测，得出了提高放顶煤液压支架可靠性的根本途径是用两柱式取代四柱式；张守祥[4]对液压支架试验室试验结果进行统计，总结了几类典型故障，得出了影响液压支架整机可靠性的几类因素；苏林军等[5]对液压支架各部件功能关系进行了分析，绘制了液压支架整机串、并联可靠性功能逻辑图，得出了可靠度计算公式；赖明荣[6]根据模糊劣化指数理论提出了基于状态检测的寿命研究方法，并对液压支架整机进行了寿命预测和状态评估；李博[7]对液压支架工作阻力数据进行了采集，并使用有限元分析软件结合采集数据，对液压支架的工作寿命进行了预测；武红霞等[8]通过ANSYS的概率有限元模块对液压支架顶梁可靠度进行了分析，说明了载荷和材料性能的随机性会影响液压支架的可靠度；洪岸柳[9]对液压支架结合工程有限元模拟分析和实验室应力应变试验，对液压支架进行了强度分析及疲劳特性研究，研究表明分析结果与测试值基本一致，并进一步分析了寿命情况；MA Yuan-yuan等[10]通过有限元模拟仿真和压架试验，研究了液压支架各结构的应力情况，并对此进行可靠性定性分析；Prebil等[10]研究了直接关键运动机构四连杆，并实现长度优化，提升了机构运动精度可靠性；马园园[11]等根据支架与围岩的相互作用关系，采用Monte Carlo模拟法获得了载荷幅值和均值的分布。

尽管以上的相关研究对液压支架可靠性预测有很大贡献，但研究多数为定性分析和疲劳寿命分析，尚未给出通过液压支架架型试验预测液压支架可靠性的定量分析方法。针对以上问题，将研究如何通过液压支架架型可靠性试验，获得液压支架关键构件——顶梁的可靠性情况。

1 顶梁结构疲劳可靠性模型

一般机械结构的可靠性模型为应力-强度干涉模型，在强度和应力相互独立的条件下，两者之间的概率关系如下式：

P(δ|s)=P(δ)

式中，P为事件发生的概率；s为顶梁结构的广义应力；δ为顶梁结构的广义强度。

对于液压支架顶梁的可靠度和失效概率而言，当顶梁的应力s大于强度δ时，顶梁将发生失效。故规定其功能函数为[12]：

实际使用过程中，由于煤矿井下顶板与围岩的不断运动，导致支架顶梁承受交变载荷，使支架顶梁部位承受交变应力。交变应力的存在，使支架材料发生疲劳损伤，表现为随着液压支架使用时间的增加，材料强度发生疲劳退化，干涉区域逐渐增大，最终发生疲劳断裂。因此，液压支架可靠度下降主要由结构材料疲劳强度降低引起，考虑结构疲劳强度随时间降低的情况，可建立液压支架结构疲劳时变可靠性预测模型，如图1所示。

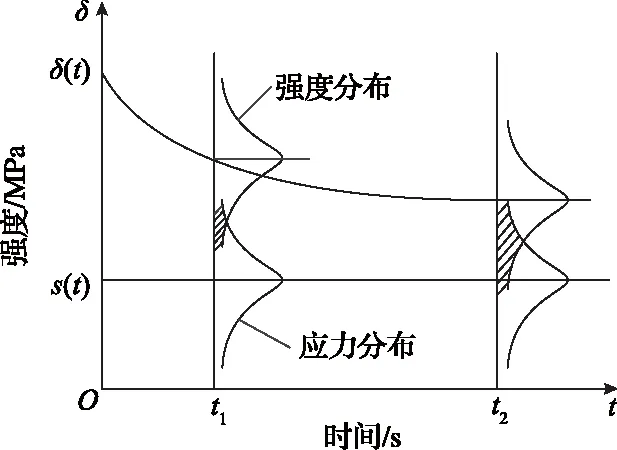
图1 支架时变可靠性模型

2 液压支架顶梁正交试验

2.1 创建顶梁三维模型

通过简化顶梁立体结构，利用SolidWorks对液压支架顶梁进行建模，并将文件设为_.x_t格式保存，导入ANSYS Workbench中，模型如图2所示，并完成等效作用点垫块布置，如图3所示。

图2 顶梁简化模型

图3 垫块布置图

2.2 网格划分

顶梁的主体材料为Q460，在ANSYS材料库中添加Q460材料属性后，选择自动划分对顶梁三维模型进行网格划分，其结果如图4所示。

图4 顶梁网格划分

2.3 顶梁正交试验设计

试验主要分析顶梁外载作用点位置对顶梁应力影响情况，采用外加载方式进行虚拟试验，假设柱窝和各铰接孔为固定约束，在7个垫块处分别施加2个水平的载荷，进行8次模拟实验。此处给出试验1的约束和载荷情况，如图5所示。

2.4 顶梁正交试验结果分析

ANSYS取8个试验中顶梁最大应力值作为试验结果，根据试验结果，采用直观分析法分析各点受力对顶梁应力影响程度，绘制因素水平趋势，如图6所示。

图6 因素水平趋势图

分析图6可知，顶梁最大应力值随1、2垫块加载力增加而增大，随着垫块6载荷的增大而有下降趋势，在顶梁中部两端和中间位置以及顶梁后端加载，顶梁最大应力受到的影响较小。由此表明顶梁前端加载对顶梁应力影响最大，对照《通用技术条件》中规定的顶梁强度试验加载方式，其中顶梁两端及扭转加载包含顶梁前端加载。两端集中加载是在顶梁两端放置长形垫块，顶梁扭转加载有两种情况，一种是前端单侧放置方形垫块，后端放置长形垫块；另一种是前端放置长形垫块，后端单侧放置方形垫块，根据图6正交试验结果，顶梁危险工况不包含垫块6(右下角方形垫块)位置加载，故扭转加载的第二种情况为顶梁的危险工况。顶梁扭转加载如图7所示。

图7 顶梁扭转加载

3 危险截面位置确定

通过以上分析，确定了液压支架顶梁的最危险工况的加载方式，下面将对顶梁危险工况下应力集中情况进行分析，根据Miner损伤法则，计算顶梁的疲劳寿命，并结合某公司支架维修情况，研究支架顶梁的危险截面。

按照图7所示布置垫片，并再次导入ANSYS Workbench中进行危险工况有限元静力学分析，求解结果如图8所示，最大应力值为438.93MPa，接近屈服强度。

图8 扭转载荷应力云图

寿命计算采用Miner线性疲劳损伤累积理论，其数学描述为：每个循环应力的最大循环应力分别为s1，s2，…，sk，对应的循环次数分别为n1，n2，…，nk，若结构到达破坏时的周期数为C，则循环应力s1，s2，…，sk的总循环数为Cn1，Cn2，…，Cnk，对于σ1对构件造成的损伤为：

D1=Cn1/N1

σk对构件造成的损伤为：

Dk=Cnk/Nk

因此构件产生疲劳破坏的条件为：

结构的疲劳寿命计算常用S-N曲线法，其拟合公式主要有：

指数函数

lgN=a+bs

(1)

式中，a、b为材料常数。

幂函数：

lgN=a+blgsmax

(2)

式中，a、b为材料常数。

Weibull公式：

lgN=a+blg(smax-A′)

(3)

式中：A′为理论应力疲劳极限；a、b为材料常数。

通常将钢材所能承受107～108次循环应力加载的最大应力值称为疲劳极限，其对S-N曲线有重要影响，相关研究显示，疲劳极限s与静强度极限sb之间关系如下[14]：

s=λsb

(4)

式中：A′为理论应力疲劳极限；a、b为材料常数。

当钢材的循环应力达到107次以上后，S-N曲线趋于水平，故选用107次循环加载时失效的最大应力为疲劳极限，根据实际工程经验，取λ=0.47，即N=107时：

s7=0.47sb

(5)

而当循环103次时，根据实际工程经验，取λ=0.9，即N=103时：

s3=0.9sb

(6)

为简化计算，材料Q460的S-N曲线利用指数函数公式进行拟合，其静强度极限为sb=700MPa左右，将sb分别代入式(5)、(6)后，再代入式(1)求得Q460的S-N曲线拟合公式为：

lgN=11.19-0.013s

根据上式使用ANSYS Workbench绘制材料的S-N曲线图9所示。

将不同载荷循环次数下材料的疲劳强度，录入Q460的材料参数中[15]，设置疲劳强度因子为0.8，求解顶梁疲劳寿命分析结果，如图10所示。

图9 Q460的S-N曲线

图10 疲劳寿命云图

结果表明，最大应力及疲劳寿命最低点均位于柱窝附近箱型结构上，与某公司维修情况一致，故可以确定顶梁危险截面即为柱窝附近箱型结构上。

4 算例

根据以上分析计算可知液压支架顶梁危险截面在柱窝附近箱型结构上，所以对某公司生产的某型号液压支架进行可靠性分析，应利用顶梁柱窝附近的应力值、疲劳强度，前者服从正态分布，后者可以等效正态分布，则有液压支架可靠度：

式中，β为可靠度；μδ为强度均值；μs为应力均值；σδ为强度标准差；σs为应力标准差。

R=Φ(β)

式中，Φ(·)为标准正态分布函数。

计算不同载荷循环次数下16Mn、Q460两种材料液压支架可靠度指标，并查标准正态分布表，求得液压支架可靠度见表1、表2，并绘制其可靠度曲线，如图11所示。

表1 16Mn材料液压支架不同载荷循环次数下可靠度

表2 Q460材料液压支架不同载荷循环次数下可靠度

根据图11预测曲线可知，用16Mn材料预测支架顶梁可靠性偏于保守，并且随着载荷循环次数的增加，保守量先增大后减小，可靠性预测曲线在交变载荷开始阶段衰减较快；Q460材料可靠性预测曲线衰减趋势较为平缓，在循环次数达到3×105时，衰减速度迅速增大，之后逐渐趋于平缓，衰减较慢，材料疲劳强度达到疲劳极限，支架顶梁发生失效。