多因素影响贡献度视角下矿产资源开发利益分配研究
2019-02-19黄光球聂兴信
魏 帅,黄光球,聂兴信
(西安建筑科技大学 管理学院,陕西 西安 710055)
目前,关于矿产资源开发利益分配问题,国内外学者多从税费制度和利益博弈两个角度进行了研究。张炎治,魏晓平[1]认为资源税费制度的设计缺陷是导致政府和企业资源利益分配错位的根本原因。陈占锋[2]认为矿产资源开发利益相关者存在一种不合理的利益格局。王小萍[3]从法律角度认为应重构矿产资源利益公平分配法律制度体系。周丹,熊华丹[4]认为应重点对矿产资源补偿费和资源税进行改革。王承武[5]认为必须建立矿产资源开发利益分享机制。刘春学,李连举[6]利用博弈理论和方法,构建了矿产资源开发企业和矿区居民之间的不完全信息动态博弈模型。傅建球,徐运保[7]指出了农村矿产资源开发中存在的利益分配扭曲问题。文献[8]从政府制定政策的角度实现矿产资源利益的合理分配。相关研究多是基于分配制度、调整对策等方面展开研究,对合理改进矿产资源开发利益分配体系具有较好的促进作用。但如何量化矿产资源开发各利益相关方之间的利益分配,有效解决利益分配不均及利益冲突问题,还有待深入研究。
1 相关理论文献综述
Shapley值法是由美国对策论专家LloydShapley提出的解决多人合作对策模型,常用于解决利益分配问题。徐秋爽,穆丽运用Shapley值法解决配送问题的利益分配。盛松涛考虑到合作成员贡献度对利益分配的影响。付秋芳构建了一个更合理的Shapley-RIEP模型。国外学者Yoshio Kamijo对Shapley值法成本分摊模型进行改进。Conrado Manuel考虑了合作博弈中中立人员对Shapley值利益分配的影响[9]。综上,Shapley值法没有考虑各种影响因素对利益分配的影响,实际应用中需考虑各因素建立权重体系对Shapley值分配结果进行修正,使分配结果更符合实际情况更合理。
本文的研究思路是:首先界定矿产资源开发核心利益相关者,制定矿产资源开发利益分配准则,然后构建核心利益相关者合作博弈与Shapley值法模型。本文的特色之处是:综合考虑矿产资源开发利益分配的影响因素,运用熵权法和理想点原理,对传统的Shapley值的利益分配模型进行修正,结合矿产资源开发实际案例优化利益分配策略。
2 矿产资源开发核心利益相关者界定
依据Freelman关于利益相关者的概念[10],根据在矿产资源开发中发挥的作用和利益相关的程度不同,把利益相关者分类(见表1)。在企业为责任主体、经营主体、受益主体的传统矿产资源开发模式下,政府、矿业企业、矿区居民是矿产资源开发的核心利益相关者,本文提出政府、矿业企业、矿区居民三方联合进行矿产资源开发的“属地联席”新模式,即“政府有偿出让矿产资源,矿业企业主体经营开发,矿区居民直接有效参与开发,三方共同参与经济利益分配”模式。核心利益相关者是是本文的研究对象,其在追求自身利益时,会产生利益冲突,而确保矿产资源开发顺利实施的关键在于制定科学合理的经济利益分配策略。

表1 矿产资源开发的利益相关者
基于互利共赢、收益与投入、风险相对称、公平兼顾效率的原则进行矿产资源开发利益分配。
3 合作博弈模型及Shapley值法利益分配模型构建
矿产资源开发及利益分配问题,可视为政府、企业企业、矿区居民三方进行合作博弈的问题。合作博弈由局中人集合和特征函数这两个基本要素构成[11]。局中人集合由对矿产资源开发过程有影响的独立利益主体构成,这个集合中的元素称为局中人[12]。假设某矿产资源开发中有n个利益主体,用集合N={1,2………n}表示,每一个利益主体看作一个局中人。本文把矿产资源开发利益相关者合作后取得的总收益定义为特征函数[13]。
设集合N={1,2……n},如果对于N的任意子集S都对应一个实值函数V(S),满足V(Φ)=0,利益相关方不相互合作时,不会取得收益。V(S1∪S2)≥V(S1)+V(S2)(其中S1与S2相交为空集),利益相关者合作获得的收益大于不合作获得的收益。此时称[N,V]为n人合作对策,V为对策的特征函数[14]。
Shapley值法是沙利提出的用于解决多人合作对策问题的一种数学模型。设合作博弈的集合I={1,2………},对于其子集S对应一个函数V(S),第i位合作伙伴从联盟中获得的收益为φi,公式如下:
[v(s)-v(s/i)],(i=1,2……n)
(1)
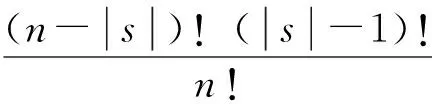
4 基于熵权法的Shapley值修正
4.1 考量多重因素影响贡献度的Shapley值修正分析
Shapley值考虑到了各成员对合作的边际贡献,避免了平均分配的弊端,但是默认各成员风险分担均等,都为1/n,但实际上在矿产资源开发的过程中,各成员风险分担、投资比重、自身的创新能力、任务执行度各不相同,而且对矿产资源开发的利益分配有重要影响。需要综合考虑多种因素,对Shapley值进行调整。因为矿产资源开发利用具有风险高的特点[16,17]。关于风险因素评价指标本文在前人研究基础上从技术风险、企业能力风险、市场风险、其他风险几个方面进行评价[18],见表2。矿产资源开发过程中需要投入很多资金人力物力[19],矿产资源开发利益相关者具备创新能力[20]。本文借鉴《基于竞合策略的供应链风险及收益分配分析》关于创新能力的相关指标,见表3。任务执行度体现各利益相关者在矿产资源开发过程中,对各类任务指标的执行程度[21]。

表2 矿产资源开发风险评价指标

表3 矿产资源开发成员创新能力指标
考量以上多重因素对矿产资源开发的影响及贡献度,建立基于多重因素影响及贡献度的Shapley值修正模型,如图1所示。
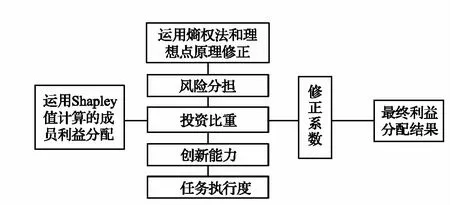
图1 基于多重因素影响及贡献度的Shapley值修正模型
4.2 基于熵权法的Shapley值修正
本文采用客观的熵权法确定权重。
4.2.1 修正矩阵计算与处理
参考孙世民[22]的研究建立如下模型:设矿产资源开发利益分配修正因素集合为J={1,2…n},第i个成员关于第j个修正因素测度值为aij(i=1,2…m,j=1,2…n),修正矩阵为A=(aij)m×n。进行如下规范化处理:
规范化后的利益分配矩阵为B=(bij)m×n。
4.2.2 修正权重的确定
采用熵权法计算修正权重[23]。设有m个成员,n个修正因素(评价指标),第j个指标下对应指标比重为Pij,
第j个指标的熵值为:
第j个指标的权重为:
4.2.3 修正系数的确定
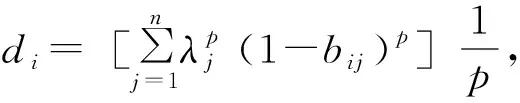
5 实例研究
收益分配主体是指在某种前提条件下获得相应份额利益的社会群体或团体,主要有政府,企业,矿区居民[26]。根据进行收益情况调研及并对历史开发所收集相关数据的进行整理,得到下表数据,各成员单独和组合开发的利益分配情况分析已知。政府,矿业企业,矿区居民分别用1,2,3分别表示,单独和组合开发的利益分配情况见表4。Shapley值法利益分配额的确定和计算过程如下:

表4 利益分配表(万元)
注:数据选自 《基于Shapley值法的矿产资源开发利益相关者利益分配博弈分析》的计算。

表5 利益相关者政府的利益分配值
由Shapley值模型计算可得,政府的利益分配值为:φ1(v)=100/3+200/6+160/6+240/3=173(万元),同理可得企业的利益分配值φ2(v)=93(万元),矿区居民利益分配值φ3(v)=54(万元)。通过向矿业领域专家发问卷,请专家从风险分担、投资比重、创新能力、任务执行度几个方面对政府,矿业企业,矿区居民三方对进行评价,得到各修正因素的测度值,修正因素的基础数据见表6。
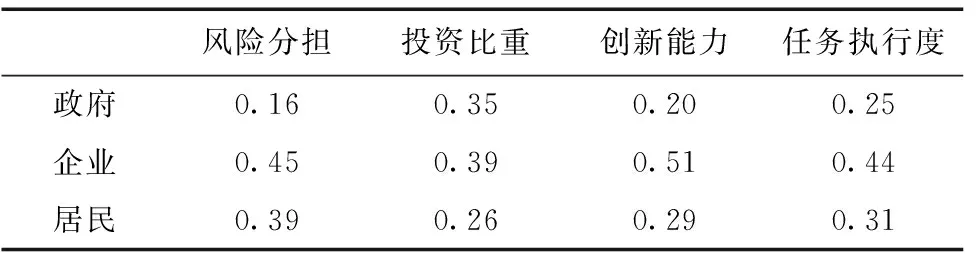
表6 修正因素的基础数据
运用熵权法计,据上文公式算各修正因素的熵值和权重见表7。
根据上述公式和方法计算修正系数和修正额见表8。
修正结果表明,修正后的利益值仍然比三方核心利益相关者单独开发矿产资源所获得的收益要大,符合合作开发的参与约束前提条件。由于政府拥有的自身资源优势,单纯从贡献度角度,获得了较大收益。综合考虑几个修正因素以后,政府由于体制原因,不能承担太大风险,创新能力有限,而企业属于风险偏好型,善于应对市场变化,勇于创新,居民承担环境破坏等较多风险,企业和居民利益分配有所增加,政府利益分配有所减少。

表8 修正过程计算结果统计表
6 结 语
考虑到各合作成员的风险分担,投资比重、创新能力和任务执行度因素,计算出各因素的熵值和权重,并计算出各成员的修正系数,对传统Shapley值法利益分配进行修正。采用多因素视角下考虑贡献度的利益分配方式,应用在矿产资源合作开发利益分配中,对各方原有利益分配额度进行调整优化,使利益分配更加科学合理,能对利益相关方起到更好的激励作用,为矿产资源开发利益分配提供了方法借鉴。但是运用该方法也存在不足,需要测算成员在各种合作组合情况下的收益值,以确定各成员的边际贡献值。
