关于半壁无限深势阱束缚态存在条件的讨论

王凯枫 时彦朋 刘建强

( 1 山东大学微电子学院，山东 济南 250100； 2 物理国家级实验教学示范中心(山东大学)，山东 济南 250100)

无限深势阱是量子力学中最基本的模型之一，对了解量子力学理论具有重要的意义，在教学和科研中都具有非常重要的作用。一维无限深势阱目前几乎是所有初等量子力学教材[1-6]中详细讲解的经典内容，半壁无限深势阱作为无限深势阱的变形，也是量子体系中较为常见和重要的模型[5]。

1 问题的提出

在量子力学教科书中，一维半壁无限深势阱问题描述如下：

如图1所示，设粒子处于如下势场中，

(1)

其中，a为阱宽；V0为势阱高度(V0>0)；分段函数的3个部分分别对应图中的Ⅰ、Ⅱ、Ⅲ区域，求解V0与a满足什么条件时，体系存在束缚态。

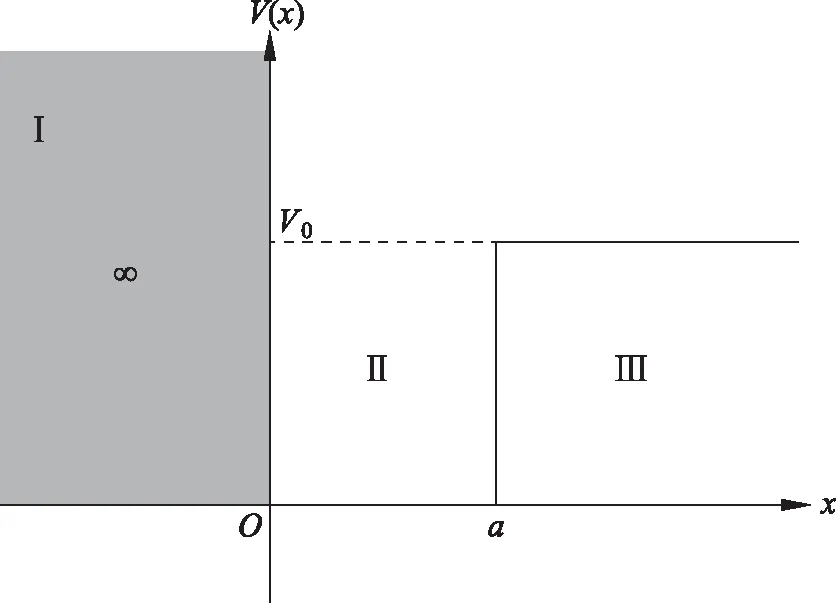
图1 一维半壁无限深势阱示意图

2 问题的传统解

体系存在束缚态时，有

此时波函数满足定态薛定谔方程

(4)

在Ⅰ区域内，V(x)=∞，ψ1(x)=0。

(5)

(6)

在Ⅲ区域内,令

(7)

有

(8)

求解方程(6)和(8),并结合连续性条件和束缚态式(3)得

由连续性条件可得

即需要求解方程(11)、(12)在束缚态条件下存在非平庸解的条件：

(13)

令

η=αa(η>0),ζ=ka(ζ>0)

(14)

得到

(17)

图2 超越方程组(15)和式(16)的图像解

据我们所知，目前几乎所有主流教科书[1-3]给出答案：式(17)为体系存在束缚态的条件。

3 分析与讨论

下面讨论关系式(17)作为解的合理性。

(18)

不符合式(14)中η>0的条件。反推η>0这一条件，可知其来源于式(7)α>0，即式(2)0

此时连续性条件仍然成立，即

ψ2(a)=ψ3(a),ψ′2(a)=ψ′3(a)

由此可得

易得式(23)恒成立。对于式(22)，若A=B=0，则有ψ(x)=0，满足束缚态条件ψ(x)|x→∞→0。但同时波函数在全空间恒等于零，即粒子在全空间内出现的概率为零，显然与题目条件不符，没有实际物理意义。

若A=B≠0，由式(21)得，当x→+∞时，ψ3(x)=B≠0，不满足束缚态条件(3)ψ(x)|x→∞→0，得此时波函数不是束缚态。

因此，最终结论为：半壁无限深势阱存在束缚态的条件严格应为

由一维半壁无限深势阱存在束缚态的临界情况推广到有限深势阱的情形(图3)，

图3 一维有限深势阱示意图

4 结论

半壁无限深势阱或者有限深势阱是量子力学的初学者必然遇到的问题，在初等量子力学中的地位不容小视，本文给出该物理模型的严格解，讨论了其临界状态的情况，指出了传统教材中就该问题的处理不足之处。本文能使人们正确认识这类问题，对于从事量子力学的教学和科研工作者有重要意义。