Automatic route planning for GPS art generation

Andre Waschk(),Jens Kr¨uger()

Abstract In this paper,we present a novel approach to automated route generation of global positioning system(GPS)artwork. The term GPS artwork describes the generation of drawings by leaving virtual traces on digital maps.Until now,the creation of these images has required a manual planning phase in which an artist designs the route by hand.Once the route for this artwork has been planned,GPS devices have been used to track the movement.Using our solution,the lengthy planning phase can be signi fi cantly shortened,thereby opening art creation to a broader public.

Keywords GPS art;walking;routing;shape detection;navigation

1 Introduction

Global positioning system(GPS)art,as it is known today,is a form of location-based tracking using GPS hardware as a digital pen to create astonishing largescale artwork.It can be considered the 21st-century version of large-scale drawings on the landscape,a concept known for millennia.As early as around 500 BCE,the Nazca culture created the Nazca Lines,which have been recognized as a UNESCO world heritage site[1].

One of the best known such works of art was created by Jeremy Wood in 2010.He was hired as a GPS artist to create a work of art,called “Traverse Me”,for the University of Warwick[2].Wood used GPS trackers to record his path as he walked across the university campus without having any immediate feedback of his taken route.After fi nishing his walk,he used the recorded data to visualize the path he walked and fi nalize his artwork.

Due to the integration of GPS into consumer electronic devices,such as mobile phones and smartwatches,recording our motions has become simpler than ever. Over the last decade,these smart devices have become more and more powerful,allowing us to compute routing solutions on the fl y right when we need them.

Over time,GPS art has also attracted the interest of sports analytics.Thanks to integrated tracking hardware,runners and cyclists have become especially interested in sharing their latest workouts with other enthusiasts on platforms like STRAVA[3].Sports devotees around the world have started running simple fi gures to give additional motivation to their daily workout programs.

Stephen Lund,a cyclist and GPS artist,described his process of planning and riding a GPS artwork in a Ted Talk in 2015[4].According to Lund,the primary process consists of glancing at a map and waiting for inspiration.The artwork presented on his website[5]is the result of this glancing-at-a-map paradigm.

Fig.1 The SIGGRAPH logo as a GPS route on top of Tokyo computed using our approach.

In our work,we target a different situation.Instead of attempting to fi nd a shape that naturally exists on a given map,in many applications it is desirable to fi nd a path for a given shape(see Fig.2)and optimize the route and its placement,size,and orientation according to the shape.

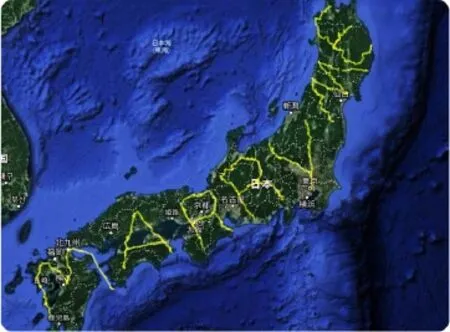
Fig.2 The largest GPS drawing recognized by the Guinness Book of World Records[6].

2 Related work

Even though the idea of GPS art has been around for several decades,to the best of our knowledge,it has never been of particular interest to the computer graphics community.

The work most closely related to our approach is the thesis of Balduz[7].He approached the GPS art problem by rasterizing the map and the target fi gure into a regular grid.He then converted the streets into a binary image where black pixels represent a street and white everything else.To compute the best possible position for the fi gure,he centered it above every pixel,computed the minimal sum of distances between the fi gure and the map image,and then selected the position with the smallest value.

The goal of Balduz’s work was to use image operators to fi nd the best possible match on the map for the given fi gure.His intention was to design the approach so that GPUs could be used to parallelize a brute force approach to the needed similarity computations.Neither a GPU implementation nor the computation of the actual route from the pixel cloud is solved,leaving both problems open for future work.Balduz makes no mention of the performance of the system.Although his result resembles the input fi gure,we consider that the discrete imageused approach of GPS art generation.Whereas the commonly used approach analyzes the road network if rst and then recognizes and draws fi gures that are implied by the road itself,we can see in this proposal that the artist had a precise image in mind,the text“Marry Me”,and was forced to fi nd his way across the islands of Japan.

A related concept,known assnakes,is used for feature detection in images[9]and triangular meshes[10].A different concept for the visualization of figures within graphs can be found in Ref.[11].None of these works,however,fit the requirements of GPS art:the route has to be a sub-graph of the existing road map.

A similar idea tailored toward the usage of drones can be found in Refs.[12,13],in which the focus is on introducing an aerial sketch of the fl ying drones’behavior in single images.Although the concept of a still image of time-varying data seems to be similar to our idea,drones are much less constrained in producing artistic sketches since they can freely move throughout the sky without any streets to be considered.based approach has numerous drawbacks compared to a graph-based solution.Firstly,it is unclear how to handle particular characteristics of the streets,such as a one-way designation,or three-dimensional information,such as bridges and overpasses,and secondly,it is unclear how to turn the pixel cloud into a connected route automatically.

Another work that explicitly addresses GPS art is that of Rosner et al.[8],which focuses on the humancomputer interaction aspect of the software supporting the route computation task.The goal of this work was to motivate users to explore the city by tracing figures sent to them by friends and annotated with little personal messages.For the route computation,Rosner et al.rely on the iOS built-in mapping system.In Section 4,we point out the problems with standard routing algorithms for the task of GPS artwork.Since Rosner et al.mainly focus on the input and community aspect of GPS art and consider routing as a black box,it should be straightforward to integrate our solution with their application.

In the fi eld of GPS art,the most massive GPS artwork traversed by a man on foot,and recognized by the Guinness Book of World Records,is a 7.163 km long marriage proposal by Yasushi Takahashi(see Fig.2).Besides the considerable length of the artwork,it also differs in another way from the widely

3 Contribution

The contribution of this paper is a novel algorithm for route generation that is speci fi cally tailored for the generation of GPS art routes.In contrast to the widely adopted process for the creation of GPS artwork,as described by Lund[4],our approach automatically computes an eye-pleasing route and opens the artistic style of GPS art to a broader public,enabling users to generate GPS artwork for any speci fi c fi gures they choose,e.g.,a marriage proposal,a company/brand logo,a name,a date,or other text.More speci fi cally,the algorithm takes as input the map region,starting position,and additional parameters de fi ning the quality metrics of our approach,such as desired maximum length of the route to compute the fi nal artwork.From this data,our approach computes a route that resembles the input fi gure much better than any off-the-shelf mapping solutions.

As we do not require additional data structures or any precomputation,we anticipate that our proposed solution can be easily integrated into existing mapping solutions such as Google Maps[14],Bing Maps[15],or other popular software and services.

4 Issues with standard solutions

The prevailing idea for the creation of routes for GPS artwork is to use existing routing algorithms that are widely available on mapping solutions and navigation systems.On closer examination,however,it becomes clear that these systems optimize the routes for goals that are very different from the ones necessary for the creation of GPS artwork routes.Figure 4 illustrates a typical problem arising from using conventional routing algorithms for the creation of GPS artwork routes.To the best of our knowledge,existing software uses variations of three criteria for the optimization of the route:time,price,or distance.Depending on the underlying criteria,the routing reduces the details of the fi nal GPS artwork shape.Time favors streets with higher speed limits than streets that are closer to the fi gure.Price avoids various kinds of charges and minimizes fuel costs not related to the target shape.The last widely used optimization,distance,minimizes the length of the calculated route.Depending on the fi gure,this reduction in length,in turn,reduces the details of the fi nal GPS artwork.

As can be seen in Fig.4,the approximation of the line produced by Google’s mapping solution inadequately represents the desired input,whereas our solution delivers a much closer approximation.Curiously,Google’s solution is particularly problematic in cities with a checkerboard-like road pattern.In these cities,one would expect a standard distance-based solution to work,but within this kind of street pattern,numerous shortest routes exist between the two points,due to the Manhattan-Distance being the same for multiple routes.In this speci fi c case,the routing software prefers main streets with their higher speed limits and a minimum number of turns needed to reach the destination.

An obvious mitigation attempt is to insert more points along the outline of the shape and thereby force the system to more closely approximate a given shape.Starting from a coarse shape,more intermediate points do improve the route with shortest distance optimization,but with increasing density of these points,the result quickly degenerates(see Fig.4).

Another problem with standard routing algorithms is the resolution of points that are not directly placed on a street.All solutions we analyzed snap these off-grid points onto streets that are predetermined for the area of the original point location. The process of repositioning off-grid points is a reasonable choice for the standard use of routing software,where users mostly desire to get to a point on the street corresponding to the selected location(e.g.,entrances of parks,a large building,etc.).In GPS art,however,the goal is to approximate the overall shape of a fi gure and not to reach every control point.Consequently,missing a control point of the shape by some distance is preferable to a lengthy detour that would disarrange the appearance of the entire shape(see Fig.3).This situation is particularly problematic with large naturalobstacles,such as lakes,rivers,parks,or mountains.In such situations,standard mapping solutions can introduce almost arbitrarydetours.

To generate pleasing and desirable GPS artwork,the optimization goals are signi fi cantly different,and,to the best of our knowledge,no available routing software offers speci fi c optimization methods for this situation,even though there exist exciting applications of this technique for the broader public(see Fig.2).

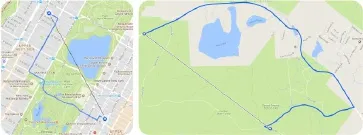
Fig.3 Due to the underlying routing approach and targeting,standard routing approaches fail to locate control points that are off-grid.In this case,massive detours occur that are undesirable for GPS art.

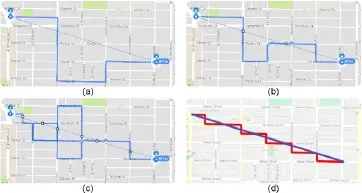
Fig.4 Approximating a single line shape with Google Maps.Using just the start and end points creates a route that signi fi cantly deviates from the diagonal line(a).Adding more points(b).With too many points,the line starts to incoprporate numerous U-turns to guarantee that each way-point is reached(c).Our solution is given in(d).

5 System overview

We present an automated system for generating routes for GPS artwork. The fi rst input to our system is a fi gure drawn by the user as well as text,input via a keyboard.Our system supports basic transformations,such as scaling,rotation,and translation of the text and brush strokes made.The text is converted,using a simple font-rendering engine,to a list of line segments,such as brush strokes.Our implementation uses street data obtained from the Open Street Map(osm)project[16].At runtime,we stream the osm data of the current area and extract the street information found within the data on the fl y.For faster computation,we build a bidirectional graph of the street network,where each node represents a physical point on the street found in osm’s XML data structure.These nodes cross between different streets or points between line segments to approximate curved streets.The restructuring of the data allows faster access to neighboring nodes. Thanks to our data streaming approach,users can choose any location on the globe to create GPS artwork without thinking about any data constraints.In the next step,our system computes the route via a divide and conquer approach,processing the line-list line by line.We use a single-source,multiple-target,shortest path algorithm similar to Dijkstra’s algorithm[17]that minimizes a speci fi cally tailored distance metric explained in Section 7. The system works at interactive rates and performs parameter changes,with immediate feedback.Once a satisfactory route has been computed,our system outputs the route as an overview image as well as a list of turn-by-turn navigation instructions.

6 Algorithm overview

Our approach can be summarized as follows.We start by selecting the fi rst segment of our original fi gure and then the longitude and latitude of the starting position(see Fig.5).Based on these coordinates,we determine the closest node of our graph as the starting position for our GPS path.Once the starting node has been determined,we compute the path from the start to the end of the segment by evaluating the cost function described in Section 7.

After approximating the end position of the fi rst segment,the algorithm selects the next segment starting from the last end position.We reuse the resulting end node of the previous segment as the new starting position to guarantee a continuous path across all segments once the algorithm is fi nished.

Fig.5 Left to right:placing a user-drawn fi gure on the map,selecting the fi rst segment depending on the minimum segment length,and computing the path of the segment.

7 Cost function

7.1 Basics

Our approach is based on the concept of a singlesource,multiple-target,shortest path algorithm similar to Dijkstra’s algorithm.The result of this algorithm is the shortest path within a graph starting from a given node.With Dijkstra’s algorithm,each edge is weighted by a de fi ned cost function,which results in a path with the lowest cost.

We de fi ned a completely new cost function that depends on the fi gure drawn by the user. We incorporate several metrics within our function to compensate for different edge cases that occur due to the nature of modern streets.

The cost between two connected nodesPandNis de fi ned by the function

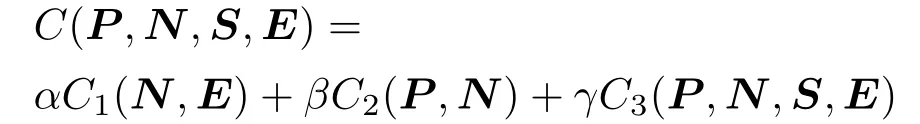
whereC1,C2,C3describe different conditions for the relationship between the street graph and the if gure segment,which is de fi ned bySandE.The weightsα,β,γare used to de fi ne the in fl uence of different metrics on the overall cost.The fi nal cost of a single path that ends as close as possible to the segment’s end positionEis computed using Dijkstra’s algorithm.

7.2 Metric:Distance minimization

Our fi rst assumption was that to reach the end of the segmentE,we have only to pick the nodeNwith the smallest distance toE.By selecting such nodes,we can guarantee to at least minimize the distance toEand therefore move toward the end of the segment(see Fig.6).We de fi ne functionC1as

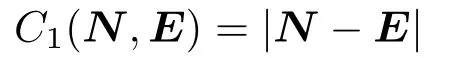
This metric can also be found in various navigational systems and therefore underlies those drawbacks described in Section 4,but it is a good start for further investigation.

7.3 Metric:Path minimization

We found that by adding a path minimization metric,as used in Dijkstra’s algorithm,we can increase the quality of our GPS artwork route(see Fig.8(top)).We de fi neC2as

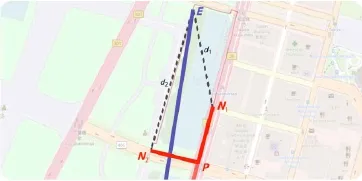
Fig.6 A distance-based decision would favor nodeN1,even though N2would be the better choice.

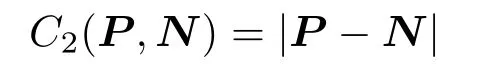
Using this metric,we prioritize nodes that are closer together,which counteracts the problems ofC1to a large degree.However,this metric has no knowledge of the input shape and cannot be used on its own to compute any feasible route(see Fig.7).

7.4 Metric:Distance sum minimzation

In several cases,a combination of metricsC1andC2led to a reasonable approximation of the original shape.However,this straightforward solution ignores the spatial distance between the route and the input shape.Figure 8 demonstrates such an issue,for which there is no incentive for a route to return to the original shape before the target point once it has deviated.

The underlying idea of this decider is to compute the distance between the fi gure segment and two neighboring nodes of the graph. We based our approach on the Riemann sum[18]and developed a function that computes the distance between two lines.

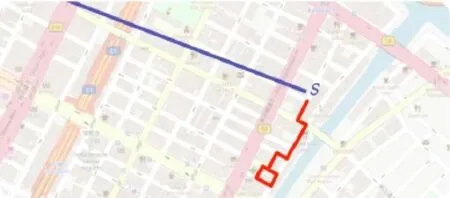
Fig.7 Using travel minimization alone results in paths with no connection to the original segment,leading to never-ending loops.

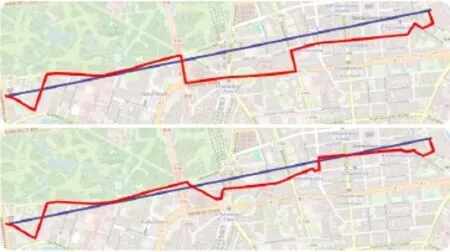
Fig.8 Comparison of different cost functions.Top:usingC1andC2 to approximate the segment.Bottom:addingC3to the cost function.

For a given segment starting at a pointSand ending at the pointE,we compute the distance sum for the pointPand each neighborNby evaluating the function:

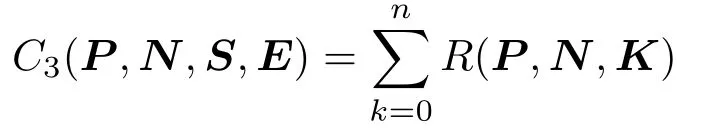
where the functionRdescribes the distance between the edge of the graph and an equally distanced pointKon the segment.The pointKis de fi ned by

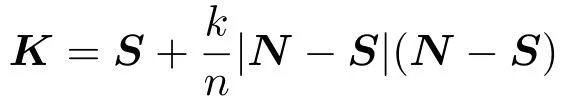
and evaluation by

wherepdescribes the projection ofKonto the segment by computing the dot-product:

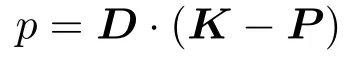
withDbeing the directional vector of the edge starting from pointP:

Based on the valuep,we can decide whether pointKis located on an orthogonal line betweenPandEor if it is found before or behind the edge.Using this information,we can evaluate the previously mentioned term and compute the distance factor of the pointKand the edge of the graph.

The resulting sum(see Fig.9)provides the best indication of the difference between the segment and the current edge and enhances the approximated path to a greater degree.

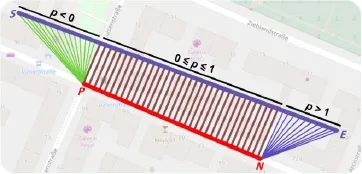
Fig.9 Representation ofC3for a given line segment betweenSand E and the current graph position P.

8 Results and outlook

In this paper,we have presented a new approach to the creation of GPS artwork routes.We have demonstrated the drawbacks of widely used routing solutions and addressed their shortcomings by implementing a new way of routing optimization(see Fig.10).

We reduce the time users have to spend planning an elaborate work of art to a minimum by offering easy-to-understand parameters.We strongly believe new interest in GPS art can be stimulated,and by integrating our approach into platforms that are already used for GPS art,a new generation of artists will be motivated.

We found our system to perform well in a broad range of fi gure and map setups.These setups ranged from simple shapes to lines of text with logos placed on many different maps.We tested our solution on the checkerboard pattern of modern cities and thechaoticstreet maps of historic cities,but there are obvious limits to our solution.In rural areas with very few streets,small complicated fi gures cannot be approximated reasonably without leaving the street network.Also, fi ne structures are generally hard to map to the street network(see Fig.11).

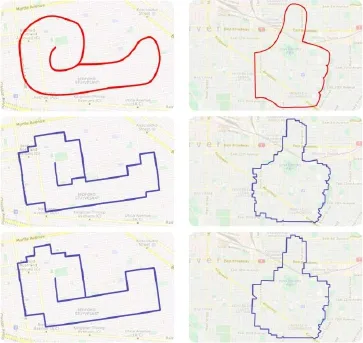
Fig.10 Computing routes for a snail and a thumbs-up fi gure using our algorithm.Top:actual drawing of the fi gure.Middle:result using a heavily favoredC3.Bottom:mainly basing our cost function onC1 and C2.

In future,we will conduct a user study to further evaluate the quality of our algorithm in comparison to standard routing solutions.We are aiming for a better understanding of our metrics and how the resulting artworks,based on our costfunction,are received by users.Our current goal is a local and global optimization by implementing an automated approach for the placement,rotation,and scaling of the fi gure based on different conditions.We will also investigate to what degree our metricC3subsumesC1andC2.

Fig.11 Limitations of automated GPS art route generation.Top:an overly detailed fi gure placed within a checkerboard pattern where details get lost.Bottom:placing fi gures within rural areas with insufficient streets.

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License,which permits use,sharing,adaptation,distribution and reproduction in any medium or format,as long as you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons licence,and indicate if changes were made.

The images or other third party material in this article are included in the article’s Creative Commons licence,unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use,you will need to obtain permission directly from the copyright holder.

To view a copy ofthis licence, visit http://creativecommons.org/licenses/by/4.0/.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095.To submit a manuscript,please go to https://www.editorialmanager.com/cvmj.