考虑资源约束和数量折扣的联合补货-选址库存协同优化研究

王 林， 郑贵莲， 曾宇容

(1.华中科技大学 管理学院，湖北 武汉 430074; 2.湖北经济学院 信息与通信工程学院,湖北 武汉 430205)

0 引言

联合补货问题(Joint Replenishment Problem, JRP)是指对所需的商品按组从供应商处进行采购，达到分摊主要准备成本、节约采购总成本的目的。联合补货策略在生产和库存系统中，是一种有效的降低成本的采购方式。作为库存领域的一个关键问题，JRP的学术价值和实用价值一直备受关注[1,2]。如沃尔玛、家乐福等国外知名企业在中国利用联合采购来获得物美价廉的物品。部分学者对经典JRP进行了拓展，并将其与选址问题协同优化，从而进一步提高实用性，其实这也更符合企业管理实践。以沃尔玛为例，其配送中心一般设立在100多家零售店的中央位置，也就是配送中心设立在销售主市场。这使得一个配送中心可以满足100多个附近周边城市的销售网点的需求；另外运输的半径较短且比较均匀，基本上是以320公里为一个商圈建立一个配送中心。目前，它在美国拥有60多个配送中心，服务着4000多家商场，这些中心按照各地的贸易区域精心部署。通常情况下从任何一个中心出发，汽车可在一天内到达它所服务的商店。据统计，其配送成本占销售额2%，是竞争对手的50%。竞争对手一般只有50% 的货物进行集中配送，而沃尔玛百分之九十以上是进行集中采购与配送。不难发现，单独考虑配送中心的选址问题或单独考虑联合补货问题，均有可能会产生次优化决策。因此，当企业需要建立或新增配送中心时，应综合考虑候选配送中心的建设成本以及它所服务顾客的需求等因素。

如何从多个候选点中选择出合适的地点建设配送中心，并确定最优订货方案，是决策者亟待攻克的难题。构建基于联合补货策略的选址-库存问题(Location-Inventory-Problem, LIP)模型是一种有效的解决方式。当联合补货与选址库存结合时，这类问题统称为JR-LIP模型。由于其数学性质比JRP更复杂，目前相关研究还很有限。Silva & Gao[3]首次建立了基于补货策略的LIP模型，并提出贪婪随机自适应搜索法(GRASP)来解此模型；与传统JRP不同的是，JR-LIP是指同一商品不同配送中心的联合补货。Wang, Qu, Chen, et al.[4]在文献[3]研究基础上，提出了确定需求下基于JR策略的选址-库存问题模型，其中定义了一个新的决策变量—最大配送中心数量，对模型进行了改进，同时设计了自适应差分进化算法(HSDE)对模型进行求解；在文献[4]研究基础上，Qu, Wang & Liu[5]分别研究了随机需求下的基于联合补货策略和独立补货策略的选址-库存协同优化问题，设计了基于HSDE算法的求解方案，通过对比实验和参数敏感性实验，分析协同优化时两种不同补货策略的优劣，为企业制定补货、选址策略提供辅助支持。经典的JRP模型中，总采购成本包括主要准备成本、次要准备成本和库存持有成本；假设需求确定，主要准备成本、各商品的次要准备成本以及单位库存成本均为已知常量；商品的单价与订购数量无关。然而，有时供应商为了鼓励顾客多购买商品，规定凡是每批购买数量达到一定范围时，就可以享受价格上的优惠，这种价格优惠即是数量折扣。不少学者对此问题进行了研究，是否选择数量折扣或选择何种折扣，目标仍然是选择总成本最小的方案。Pirkul & Aras[6]模型中讨论的是多商品的经济批量订货问题，假定每种商品都有独立的价格折扣；Moon, Goyal & Cha构建了有数量折扣的JRP模型[7]，并在此基础上考虑运输容量约束，然后利用遗传算法(Genetic Algorithm, GA)求解其模型；Cui, Deng, Wang, et al.[8]同时考虑两种折扣类型(联合补货中有的商品采取单品折扣而有的采取增量折扣/不折扣)，并设计了新颖的蝗虫群算法来求解所构建模型。企业选址与采购管理中经常面临不确定的决策环境与约束，例如：(1)缺货预约现象，当存量降到零时，不一定立即补充，允许一段时间的缺货，但到货后立即将缺货量补齐(比如“双十一”/“618”购物节)；(2)有些供应商为了获得规模效应，经常提供数量折扣鼓励零售商采购更大批量的货物；(3)运输工具不可避免地存在最大载重量限制等。考虑到这些更贴近企业运营管理的现实情况，本文对文献[3]进行了拓展，构建了一种新的考虑数量折扣的JR-LIP协同优化模型，该模型允许缺货，考虑到可用采购资金和运输工具最大载重量双重约束，具有较重要的科学意义和较高的实用价值。

这类模型研究的一个瓶颈在于高效稳定求解算法的设计，Esther, Dev, & Robin[9]证明了JRP为NP-complete问题，Amaya, Carvajal & Castano[10]指出寻求较好的启发式算法也是JRP研究的一个热点。目前已存在相对成熟的算法，如动态规划、分支定界法、Lagrangian松弛法、启发式算法等。然而当联合补货与选址相结合，并且考虑数量折扣、资金和运输容量约束时[11,12]，JR-LIP模型的求解难度更高。而传统方法自身存在不容忽视的缺陷：(1)枚举法：当问题规模比较大时，效率相对较低；(2)启发式算法：一般是针对特定的问题分析其特征，且必须找到特有的启发式规则来求解，算法不具通用性；(3) GA：实验结果证明GA总体上是一种可行的方法，但其操作复杂、算法搜索效率较低[12]。因此迫切需要找到一种高效的方法来解决JR-LIP这类问题。

差分进化算法(Differential Evolution, DE)保留了基于种群的全局搜索策略，降低了遗传操作的复杂性，在诸多领域得到应用，如Wang, He, Wu, et al.重新设计了DE，以解决异质商品次要订货成本互相影响的JRP问题[13]；Qu, Wang & Zeng设计了自适应混合差分算法(Adaptive Hybrid Differential Algorithm, AHDE)来求解JRD模型[14]，其模型考虑了因异质商品(如橡胶与化工产品)不能同车运输而产生的惩罚成本，但上述混合算法收敛精度待提高。

本研究同样基于DE，设计了融合模拟退火思想(Simulated Annealing, SA)的自适应差分算法(ASADE)对所构建JR-LIP模型进行求解。SA通过在搜索过程中设计一种不断变化的且最后接近于零的概率突跳性，能够有效避免陷入局部最优从而达到全局最优[15]。另外，SA 算法较强的局部搜索能力有利于提高DE收敛精度，且SA 算法中的Metropolis 接受准则也能提高种群多样性。为了提高全局搜索能力，该ASADE初始化两个种群使其独立进化；同时分别在双种群的选择操作中引入模拟退火思想以增加种群多样性。算例结果表明ASADE优于AHDE、改进的蛙跳算法(Frog Leaping Algorithm, FLA)及自适应差分-蛙跳算法(ADE-FLA)，从而为解决此类问题提供一种新方法。

1 问题描述及模型构建

1.1 问题描述

本文研究的模型中，考虑的是单一商品。传统的联合补货策略中，是某一企业或中心仓库对不同商品进行联合补货；而本问题中，所谓联合补货是指同一商品不同配送中心的联合补货。因此配送中心根据所分配顾客的需求，确定商品的总需求，并从外部供应商处采购商品满足所分配顾客的需求，图1为JR-LIP问题的一个示意图。

图1 JR-LIP结构示意图

1.2 模型假设与参数标识

本文构建的联合补货-选址库存模型(JR-LIP)假设条件如下：①顾客需求确定，且服从均匀分布(考虑到研究的循序渐进性，与文献[3～5]等模型假设相同)；②允许缺货；③配送中心可以服务任何一个顾客，但是每个顾客有且只能接受一个配送中心的服务。该模型中涉及的参数标识如下：

i:潜在配送中心i，1≤i≤n；j:表示顾客j，1≤j≤m；w:商品的单位重量；W:运输工具的最大载重量；B:购买资金限额；S:补货行为发生时产生的主要订货成本；Qi:配送中心i的补货量；C(Q):配送中心联合采购商品的价格函数；Ti:配送中心i的补货周期；Ti,1:配送中心i存储量为非负的时间周期；Ti,2:配送中心i缺货周期；bi:配送中心i的最大库存量；ai:配送中心i的缺货量；fi:潜在配送中心i的建设成本；TC:总成本；cij:配送中心i与顾客j之间的距离成本；si:补货行为发生时，配送中心i的次要订货成本；hi:配送中心i中商品的年平均单位库存维持成本；pi:配送中心i中商品的年平均单位缺货损失成本；Dj:顾客j对商品的年平均需求率，是已知常量。

其中，S为每次补货所发生的固定成本，包括相对固定的人员成本、与供应商联络的差旅费、运输费用、调度费用等成本；同时参与联合补货的配送中心i会产生一定的与订货数量有关的订购费用，即次要订货成本si，包括发出订单的手续费、包装装卸费、验收费等支出。在一次补货活动中，S只发生一次，参与联合补货的配送中心都发生一笔次要订货成本。

该模型的决策变量如下：

ki:配送中心i的周期乘子，ki为正整数；T:联合补货基本周期；Xij:如果Xij=1则由配送中心i向顾客j提供服务，否者Xij=0；Yi:如果Yi=1则在潜在点i建立配送中心，否者Yi=0。

1.3 数学模型

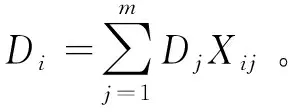
图2 配送中心i存量变化图

(I)联合补货成本CR

由于该模型考虑的是单一物品的JR-LIP，故可以将模型中不同配送中心的需求看作是不同物品的需求进行联合补货。因此，联合补货成本包括订货成本Cs、库存持有成本CH、缺货损失成本Cp，具体如下：

(1)

(II)选址与配送成本CL

(2)

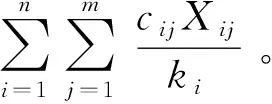
(III)购买成本Cpurchase

由于该模型研究的是有数量折扣的单一物品的多配送中心JR-LIP，因而购买成本考虑的是多配送中心联合采购这一商品的数量折扣。即商品单价由所有配送中心的采购总量Q决定。

(3)

因此，系统优化的目标是年总平均成本TC=CR+CL+Cpurchase最小化，模型如下：

(4)

(5)

1.4 模型分析

从式(4)不难看出，总成本函数TC关于配送中心最大存储量bi具有与经典EOQ类似的性质，关于决策变量基本补货周期T具有与经典JRP类似的性质。因此，求解如下:

令∂TC/∂T=0，得bi=piDikiT/(pi+hi)

(6)

由于模型为协同优化模型，决策变量ki、Yi与T相互影响。例如，Yi不仅受选址成本影响，同时也受补货过程的成本影响。决策变量T的确定，通过总成本的分析获取；而T取值又反过来影响其他决策变量取值。

将式(6)带入目标函数(4)中，再令∂TC/∂T=0得

(7)

每次采购过程中，满足购买资金约束和载重量约束的最大基本周期分别为:

(8)

因此，最优基本周期T*=min{T1,T2,T3}。

2 模型求解算法设计

2.1 基于模拟退火的自适应差分算法(ASADE)

标准DE算法中，有两个重要参数—变异因子与交叉因子[16]。变异因子F控制差分向量的缩放比例，变异因子过小，无法保证种群的多样性，容易出现早熟现象；变异因子过大，算法搜索效率低，求得的全局最优解精度低。交叉因子CR为交叉概率常数，以保证实验向量至少有一维变量是由变异向量贡献的。与变异因子不同的是，CR越大，变异向量对实验向量的贡献越大，有利于局部搜索；反之，则有利于保持种群多样性[17]。

为更好地平衡搜索效率和精度，ASADE算法调整标准DE中固定的变异因子F与交叉因子CR为随进化代数自动调整的变动参数。此外，ASADE采用双种群独立进化，并在各自选择操作中引入模拟退火思想，以增加种群多样性。具体描述如下：

1)采用双种群独立进化机制

自适应模拟退火-差分进化算法(ASADE)采用双种群独立进化机制，为使两个种群尽可能呈现较大的差异性，分别采用DE/rand/1/bin和DE/best/1/bin的变异策略生成变异个体。从理论来说，这种策略能够避免单一种群多样性的丧失，确保整个算法在更大的范围内进行搜索优秀个体，从而提高算法的全局寻优能力。

DE/rand/1/bin和DE/best/1/bin两种变异策略无论在函数求解还是模型优化方面，都具有广泛的适应性。这两种变异策略的区别在于变异操作中应用的基向量、差分向量及其数量的不同。常用的DE/rand/1/bin和DE/best/1/bin分别由(9)式和(10)式产生变异个体：

vr,G=xr1,G+F×(xr2,G-xr3,G)

(9)

vr,G=xbest,G+F×(xr1,G-xr2,G)

(10)

由式(9)可知，DE/rand/1/bin中变异个体Vr,G的基向量与差分向量是由三个互不相同的父代随机个体(r1,r2和r3)组成，因此其全局搜索能力强，种群多样性较好，但收敛速度较慢。由式(10)可知，DE/best/1/bin由Xbest引导寻优，随机搜索能力随代数的增加而下降。因此其局部搜索能力强，收敛速度快，但此种策略易导致算法陷入局部最优。根据两种变异策略的互补特性，ASADE采用双种群独立进化机制，进而平衡算法的全局探索与精度搜索能力。

2)变异因子与交叉因子的改进

两个子群分别设为pop1与pop2，其个体对应的变异因子为oF与mF，交叉因子为oCR与mCR。

(1)子群pop1采用DE/rand/1/bin的变异策略，其中oFr,G=randcr(uf,0.1)oCRr,G=randnr(ucr,0.1)。对于每一个个体而言，Fr与CRr都分别服从均值为uf、ucr的柯西分布(Cauchy distribution)和正态分布(Normal distribution)[18,19]。这两个均值uf、ucár的初值均设为0.5，然后以(11)与(12)式更新。

uf=(1-e)×uf+e×meanL(SF)

(11)

ucr=(1-e)×ucr+e×meanA(Scr)

(12)

式(11～12)中参数e是已知常数，Sf和Scr分别存放两子群中适应度值优于父代的实验个体所携带的相关参数。随着种群进化，每隔inter代，将其清零。Sf和Scr是两个参数集合，其均值分别以莱默平均和算术平均计算得到，如式(13～14):

(13)

(14)

(2)子群pop2采用DE/best/1/bin的变异策略，其中mF与mCR是由oF和oCR根据式(15～16)变异得来，目的是增加种群多样性。

mFr,G=oFr,G+rand(0,1)×(oFr1,G-oFr2,G)

(15)

mCRr,G=oCRr,G+rand(0,1)×(oCRr1,G-oCRr2,G)

(16)

(3)选择策略的改进。两个子种群独立进化，分别对其进行变异、交叉、选择操作。在选择过程中，引入模拟退火思想。模拟退火机制是模拟固体退火过程，在退火迭代中，按照Metropolis准则既接受目标函数值较好的解，又以一定概率接受较差解，因此能避免算法过快地陷入局部最优解中，从而提高算法的全局搜索能力[20]。模拟退火算法原理简单、用法灵活，将其引入自适应差分进化算法当中，可以有效地缓解DE的选择压力，增强种群进化后期的收敛性。设置退火初始温度t0=1000，退火过程中温度tG=t0×(0.99)^G，其中G为进化代数。Metropolis准则是指算法接受新解的概率。对于目标函数取最小值的优化问题，SA接受新解的概率为

(17)

2.2 基于ASADE的改进JR-LIP求解流程

1)种群个体表示

与求解标准JRP不同，本模型中配送中心的选址变量Yi、基本补货周期T和周期乘子ki，应根据供应商提供的数量折扣确定。在ASADE中，种群个体的空间维度为m+2n+2，其中Xi=(allocation(j),ki,TC,T,Yi)。个体编码包括三部分：

(1)客户分配方案：每个个体所携带的信息中，第1个位置到第m个位置代表顾客，其数值表示为该顾客服务的配送中心编号；

(2)补货周期乘子ki：第m+1到第m+n个位置代表配送中心，其取值表示该配送中心的补货周期乘子ki；

(3)模型待求参数：第m+n+1个位置表示总成本TC，第m+n+2个位置代表基础补货周期T，第m+n+3个位置到第m+2n+2个位置的取值表示选址变量Yi。

2)算法求解步骤

基于ASADE求解改进JR-LIP的流程如图3所示，算法步骤简要分析如下：

步骤1种群初始化：对ASADE算法的参数和常量进行设置，产生两个初始种群。

步骤2计算种群个体适应度值：当个体Xr,G确定以后，即可求解确定个体的适应度值。

步骤3变异操作：首先根据当前迭代次数，求出自适应oF与mF值，然后分别对pop1与pop2执行变异操作，得到两组变异向量。

步骤4交叉操作：首先根据当前迭代次数，求出自适应oCR与mCR值，然后分别对pop1与pop2执行交叉操作，得到两组实验向量。

步骤5选择操作：利用改进的选择策略，分别对pop1与pop2执行选择操作，得到两组最优个体X1best,G与X2best,G，将两者中适应度值较小者作为当代最优个体Xbest,G。

步骤6判断收敛：选择操作结束后，先更新参数，再判断循环是否达到给定最大迭代次数MaxG。当迭代次数达到指定MaxG时，迭代停止，输出结果；否则重复上述步骤。

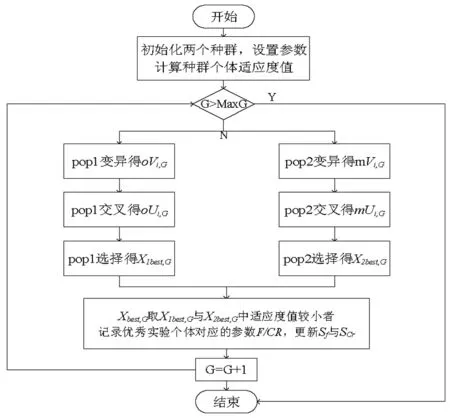
图3 求解算法流程图

3 算例与结果分析

3.1 参数设置

对比算法选择AHDE、FLA及ADE-FLA，原因如下：(1)DE算法简单高效，控制参数少，具有快速全局寻优能力，且AHDE的良好性能在类似文献研究[14]中得到证实；(2)FLA作为一种全新的启发式群体进化算法，具有高效的计算性能和优良的全局搜索能力。另外，有学者进一步将DE与FLA融合来开发精度高、稳定的混合智能新算法[21]，ADE-FLA采用自适应最大步长，审判操作以及改进局部寻优策略，来提高FLA的收敛速度和全局寻优能力，结果证明其性能较好。因此，将FLA及ADE-FLA作为对比算法较为合适。

模型的基础数据类似于文献[3]，如表1所示；价格Ci为分段函数如表2所示。对比算法FLA，Cm=0.5，Ne=50；ADE-FLA，CR=0.9，Cr=0.4，Cw=0.8,jx∈[0.2,0.4] ，Ne=50；AHDE，交叉算子CR=0.6，变异算子FF∈[0.2,0.4]。ASADE算法涉及到的参数如表3表示，种群规模NP与最大进化代数G设置统一。所有算法采用Matlab 2010b进行编码，算例都在一台配置为 Intel(R)Corei(TM)i3-2310M 2.10GHz CPU且操作系统为Windows 7的个人电脑中完成。

表1 模型基础数据

表2 价格分段表

表3 ASADE参数

3.2 对比分析

(1)为了验证算法精确度，用ASADE、AHDE、ADE-FLA及FLA四种算法对改进的JR-LIP模型同时运算5次，模型中一些参数在给定范围内随机生成，5组算例结果如表4所示：

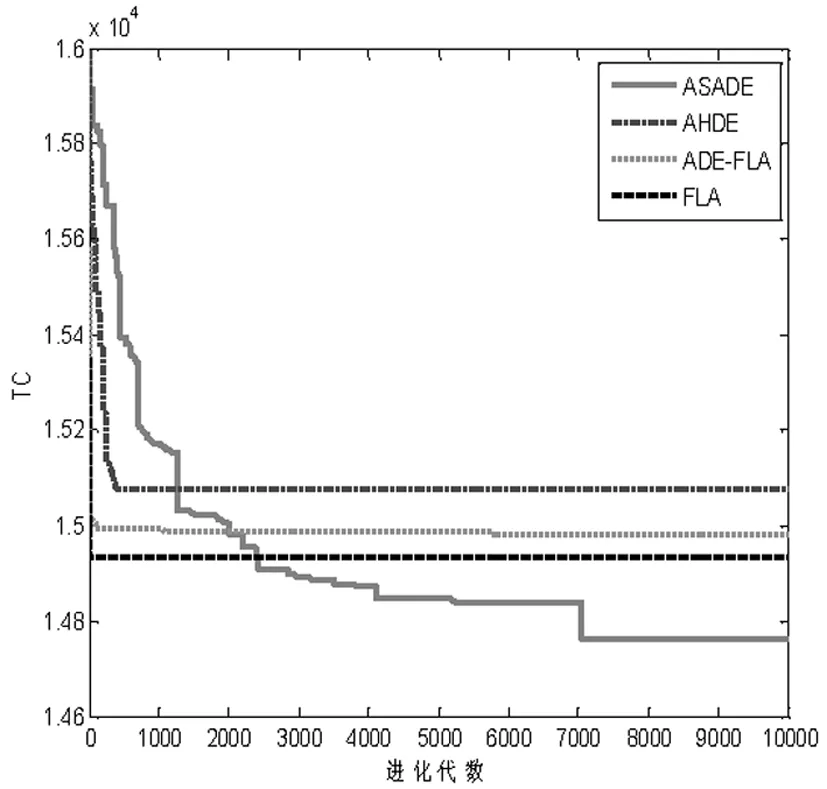
(2)为了验证算法收敛性能，以第5组为例，ASADE、AHDE、ADE-FLA及FLA四种算法求解的目标函数值随着进化代数以及运行时间(单位：秒)的收敛过程分别如图4～5所示。

从图4中可以看到，ASADE虽然收敛速度稍慢，也在可接受范围内，但是精度高；图5直观展示了运行10000代，各算法运行用时和获得的最优解，再次证实了ASADE的优势。

表4 求解结果

(3)为了验证算法的稳定性，利用上述第3组结果，用四种算法对该算例独立运行30遍，结果如表5所示。

表5 算例3求解结果

由表5可看出，当任意一组随机产生的算例固定时，ASADE总可以找到优于其他三种算法的解。根据达到最优值次数的多少可以判断出，ASADE鲁棒性优于AHDE、FLA，精确性优于ADE-FLA。综合以上分析，ASADE吸收了ADE-FLA与AHDE的优点，算例结果证明了其有效性，因此敏感性分析仅利用ASADE进行计算。

4 敏感性分析

本节将针对需求率Dj、选址成本fi、库存维持成本hi及次要订货成本si四个参数，采用单变量法对模型进行敏感性分析，讨论各参数变化后最优结果的变动情况，并记录了变化后最优成本与原成本值间的偏差，各参数的敏感性分析结果如表6～9所示。

表6 需求率Dj敏感性分析

从表6可以看出，Dj的增加或减小，对TC的影响很大，但对配送中心选址点的分布影响却不大。在现实生活中，需求往往难以确定，而本算例中，需求在±50%范围内波动的时候，对总成本的影响非常大。所以，企业在进行联合采购时，需要对商品需求进行准确预测。

表7 选址成本fi敏感性分析

从表7可以看出，在文献[3]基础上引入配送中心利用年限β参数后，由于多个计划期分摊其建设成本，从而减小选址成本变动对总成本的影响，且其对选址点分布及基本补货周期几乎没有影响。这也警示决策者在选址建设配送中心时，要保证建设质量，尽量延长其使用年限，最大程度减小选址成本对年均总成本的影响。

表8 库存维持成本hi敏感性分析

从表8可以看出，在当前假设条件之下，hi的变化对TC造成的影响很小。若hi减少50%，总成本降低0.56%，若hi增加50%，总成本增加0.48%。T随着hi的增大呈下降趋势。

表9 次要订货si成本敏感性分析

从表9可以看出，在当前假设条件下，si的变化对TC几乎没有造成影响。当si增大时，T有增大的趋势；但对于选址点的分布及周期乘子没有影响。

综上不难发现，需求率Dj对总成本的影响远大于次要订货成本si及库存维持成本hi的影响，前者最大影响可达48.24%，后者仅在0.5%左右。这说明实际情况中，若需求率预测不准将使得预算结果偏差较大。

5 结束语

本文是智能优化算法与选址-库存协同优化的交叉研究，主要工作和贡献如下：(1)考虑允许缺货的情况，研究了更具实用价值的配送中心选址与联合补货协同优化模型，首次构建了可用采购资金及运输工具最大载重量约束下有数量折扣的JR-LIP协同优化模型，该模型引入“配送中心预计利用年限”这一参数以分摊其建设成本，且引入“配送频次”这一概念说明配送成本不仅仅与配送距离有关；(2)设计了一种融合模拟退火思想的双种群独立进化的自适应差分算法(ASADE)来求解所构建的模型，其中引入模拟退火以增加种群多样性，采用双种群以平衡算法的全局探索与精度搜索能力，算例结果证明ASADE的稳定性和精确性都要优于AHDE和ADE-FLA，收敛速率也在可接受范围内；(3)对JR-LIP模型中相关参数进行了敏感性分析，分析不同参数变动对总成本的影响，可为企业科学决策提供依据。这些既丰富了选址-库存决策理论，也拓展了DE和SA算法的应用范围。正如引言中提到，综合考虑联合补货、选址和配送过程协同优化的策略被沃尔玛等企业广泛采用，从而可有效降低供应链运作总成本。

本文在研究资源约束下有数量折扣的配送中心联合补货-选址库存模型时，有待继续深入的研究方向包括：(1)考虑多个供应商的最小订货量约束等；寻找降低该模型求解算法复杂度的有效方法，从而提高求解算法的效率。(2)考虑到研究成果的更好在企业界得到应用，未来可以设计开发联合补货-选址库存协同优化辅助决策支持系统，嵌入本文构建的模型和设计的算法，从而提高决策质量和效率。