偏好情景应变式冲突分析模型

陶良彦， 刘思峰， 方志耕， 胡 骞

(1.南京航空航天大学 经济与管理学院，江苏 南京 210016; 2.南京航空航天大学 灰色系统研究所，江苏 南京 210016)

0 引言

冲突在现实世界中广泛存在，大到国家之间的贸易、军事冲突，小到企业生产经营决策。为描述、分析冲突系统，学者们提出了大量方法，例如博弈理论、亚对策分析[1]、冲突分析[2]等。冲突分析只需要定性的偏好信息，在技术转移冲突[3]、水资源冲突[4]、产学研合作[5]、复杂产品主制造商供应商间生产冲突问题[6]、供应链质量冲突消解[7]等领域得到广泛应用。由于冲突分析模型的稳定解定义在偏好信息之上，而决策者偏好信息受多种因素影响，很难确定，因此偏好分析一直是冲突分析理论与应用研究的核心问题和难点[8]。为充分考虑和描述偏好推导过程的不确定性和复杂性，学者提出了多种方法，大体分类见表1所示。

表1 冲突分析模型偏好不确定的处理方法

具体来说，Li等[9]提出用倾向(priority)、不区分(indifferent)、不清楚(uncertain)三种关系描述偏好信息不确定性，并在此基础上定义新的均衡。在模糊偏好方面，Bristow等[11]和Hipel等[12]设计了基于模糊偏好信息的冲突分析模型。孟波[14]针对偏好信息难以确定问题，也研究了决策者具有模糊偏好信息的冲突分析。在灰色偏好方面，Kuang等[15]利用灰数表征决策者偏好的不确定性，并定义了此种情形下冲突模型的灰色偏好和灰色稳定性。Rêgo等[16]定义了概率型偏好，决策者认为一个状态优于另一个状态是服从概率分布的。有学者[17,18]将第三方调解引入冲突分析中，研究为达到希望获得的最终均衡，该如何优化偏好序列。第三方机构根据这些偏好序列进行调解，确保达到满意的均衡。考虑决策者策略移动受偏好影响，Garcia等[8]提出了根据观察的策略移动推测偏好信息的方法。第七种方法基于超对策处理策略或偏好不确定情况。超对策由Bennett[20]在1977年提出，主要介绍了一个两方博弈问题，其中两个参与者对对方的偏好信息不确定，按照自身主观判断进行博弈分析，最终导致新的均衡出现。在冲突分析模型中，决策者对自身以及对手的策略、偏好信息等也会存在理解偏差现象，文献[19]利用超对策思想，首先分析决策者各自主观冲突子系统的均衡情况，进而对各决策者主观冲突系统的均衡策略求笛卡尔乘积，将此乘积定义为整个系统的均衡，最后将这些均衡细分为八种不同类型，以便分析决策。于晶等[21]考虑到决策者积极、消极、中立等态度会影响其偏好，因而将决策者态度信息引入冲突分析图模型中。考虑到偏好排序在实际中可能会受各因素干扰而发生改变，进而影响到均衡情况，Matbouli等[22]构建了评价均衡稳健性的方法。该方法基本思想是引入自由程度(The level of freedom, LoF)这一概念测度偏好改变对状态稳定的影响。如果决策者在某个状态的可行移动数目多(自由程度大)，即使偏好稍微改变就可能引起均衡变动，此时均衡的稳健性差。

以上所介绍方法是在静态情况下利用灰色、模糊、概率等不确定分析理论描述偏好信息，但在某些实际冲突分析中，偏好信息不是一成不变的，在不同情况下决策者可能具有不同偏好。例如企业在进行产量冲突决策过程中，针对经济景气程度等不同的情景，他们的偏好信息会发生变化。在经济景气时，决策者倾向于扩大生产；反之，在景气下滑时，决策者偏向缩减生产量。实际中有些冲突决策问题影响的时间跨度很大，需要考虑未来不同发展情景的影响。例如大型民用客机研制一般持续十年左右，在其研制初期进行研制周期、载客量、航程等决策时，需要考虑未来市场潜在前景的影响。针对偏好信息随不同情况变化的冲突分析问题，目前学术界还鲜有涉及。目前少数学者从动态冲突的视角考虑扩展原有冲突分析模型。例如吴育华, 程德文等[23]将局中人在可行移动范围内的移动定义为随机行为，建立起信息不完备的冲突模型。王意冈和申金升[24]将冲突视为动态过程，决策者在某一时刻向其他方向移动的概率组成状态转移矩阵，据此求出冲突事件的最终状态，即冲突均衡结果。刘勇等[25]认为冲突信息系统呈现马尔科夫特征，构建了基于马尔科夫和粗糙集的动态冲突分析方法。这些具有动态分析特征的冲突模型为分析动态情形下的冲突问题提供了很好的思路，但是实际应用中状态转移矩阵较难确定，而且也不完全适用某个时间点需要考虑偏好随情景变化的冲突问题。

Herman等[26]首次提出“情景”(Scenario)一词，他们认为未来是多样的，情景是对未来情形以及能使事态由初始状态向未来状态发展的一系列事实的描述。情景分析法是在对经济、产业或技术的未来发展等提出关键假设基础上，科学构建未来可能的各种方案，为管理者提供未来变化趋势信息，在军事、经济、突发事件应急管理等领域得到广泛应用[27,28]。例如宁钟等[29]将情景分析引入到供应链风险识别中，充分挖掘供应链中隐藏的风险，识别供应链薄弱环节。本文针对冲突分析决策者的偏好信息受未来潜在发展趋势影响，利用情景分析技术开发影响冲突决策的未来发展情景，构建偏好情景应变式冲突系统。进而从全局稳定和偏好集结两个角度定义了偏好情景应变式冲突系统的稳定。全局稳定是各种潜在情景冲突子系统均衡的交集，因此达到均衡的条件十分苛刻，可能存在全局稳定不存在情况。因而进一步设计偏好集结方法，定义偏好集结稳定，最后在案例研究中比较了这两种稳定。本文的创新性工作主要体现在以下两点：(1)考虑某些时间跨度大的重大决策中，如大型客机研制周期、航程决策，决策者偏好随未来潜在情景变化的情况，提出了偏好情景应变式冲突系统。(2)提出了偏好情景应变式冲突模型的全局稳定和偏好集结型稳定，并将这两种稳定应用在某大型客机立项论证阶段的研制周期冲突决策案例中，较好地解决了问题。

1 问题描述

经典冲突分析模型一般需要选择一个时间点，假设冲突问题在这个瞬时时刻是明朗的，决策者的偏好信息是固定的。但是在日常冲突问题中，决策者所处的环境是动态变化的，面临的未来环境多种多样。在不同的潜在未来结果下，决策者的偏好信息会发生变化。本文用“情景”描述各种潜在未来结果，分析决策者在不同情景下的偏好信息，构建偏好情景应变式冲突系统，定义与分析该冲突问题的稳定与均衡。

定义1情景[27]。“情景”是指对未来情形以及能使事态由初始状态向未来状态发展的一系列事实的描述。

定义2情景要素。情景要素是指组成未来情景的重要因素，是影响决策者偏好的关键因素。

情景要素的各种组合构成了不同的情景。根据具体的冲突分析问题，需要选择合适的情景要素。如在国防预算冲突问题中，国家经济状况以及国家周边安全形势等都是组成未来情景的重要情景要素。

定义3情景应变式偏好。决策者在不同情景下由于情景组成要素的不同会拥有不同的偏好信息，称这些偏好为情景应变式偏好。

如果在某个冲突系统中，决策者的偏好不是固定的，相反是随着未来潜在情景的不同而发展变化，则称此冲突系统为偏好情景应变式冲突系统。四元素集合常被用来描述一个冲突系统，即{N,S,A,≻}。其中N,S,A,≻分别指冲突系统的决策者集合，状态集合，转移集合以及偏好集合。这里以四元素形式定义偏好情景应变式冲突系统，具体定义如下：

下一步的任务是在偏好情景应变式背景下，定义与分析冲突系统的稳定解。本文从两个角度分析偏好情景应变式冲突系统的稳定解。第一种稳定解被称为全局稳定解，基本思想是各情景下冲突子系统的四种个体基本稳定(纳什稳定、一般超理性稳定、对称超理性稳定和序列稳定，具体定义参见文献[30])的交集分别构成整体偏好情景应变式冲突系统的四种个体基本稳定；第二种稳定解定义的出发点是将各情景偏好按照重要程度进行集结，在此基础上分析冲突系统的稳定解，这种稳定解被称为偏好集结型稳定解。最后分析全局稳定解和偏好集结型稳定解的关系。

2 偏好情景应变式冲突系统的全局稳定

定义全局稳定解的基本思路是假设在所有情景下状态si∈S都是稳定解，则称此状态为偏好情景应变式冲突系统的全局稳定。这里的“全局”是指不管未来的何种潜在情景发生，定义的稳定均成立。在任意情景冲突子系统Gk中，本文考虑四种基本稳定，即Nash稳定，一般超理性稳定、对称超理性稳定和序列稳定。

2.1 全局稳定定义

定义5全局Nash稳定(G-Nash)。假设状态是所有潜在情景下冲突子系统Gk(k=1,2,…,n)的Nash稳定，则称是偏好情景应变式冲突系统G的全局Nash稳定(G-Nash)。

根据定义1，易知下列定理成立。

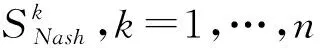
同样道理，全局一般超理性稳定、全局对称超理性稳定、全局序列稳定等定义如下。

定义6全局一般超理性稳定(G-GMR)。假设状态si是所有潜在情景下冲突子系统Gk(k=1,2,…,n)的GMR稳定，则称是偏好情景应变式冲突系统G的全局GMR稳定解。

定义7全局对称超理性稳定(G-SMR)。假设状态si是所有潜在情景下冲突子系统Gk(k=1,2,…,n)的SMR稳定，则称si是偏好情景应变式冲突系统G的全局对称超理性稳定(SMR)。

定义8全局序列稳定(G-SEQ)。假设状态si是所有潜在情景下冲突子系统Gk(k=1,2,…,n)的SEQ稳定，则称si是偏好情景应变式冲突系统G的全局序列稳定。

对于全局稳定可能出现的状态位置和稳定解数目，可以通过以下定理进行判断。

定理2全局稳定解只能出现在各潜在情景冲突子系统稳定的状态，且全局稳定数目不多于各潜在情景下的稳定解数目。

该定理根据定义容易推导，证明略。

2.2 全局稳定求解步骤

全局稳定分析可分为3步，具体如下：

Step1开发潜在情景，构建各潜在情景下冲突子系统。明确冲突分析问题的决策焦点，识别影响决策问题的关键因素(包括政治、经济、社会、技术等各方面，以决定关键因素的未来状态)，开发潜在情景。进一步分析各潜在情景下的冲突决策者、决策者策略与偏好等信息，搭建各潜在情景下冲突子系统。

Step2分别分析各潜在情景下冲突子系统稳定解。依据冲突分析稳定解定义，分析各潜在情景下冲突子系统的稳定情况。这里可以利用滑铁卢大学冲突研究实验室开发的分析软件——GMCRII进行分析，减少计算工作量。

Step3对冲突子系统稳定求交集。根据2.1节稳定解定义，偏好情景应变式冲突系统稳定解即是各冲突子系统稳定的交集。

全局稳定解是各潜在情景冲突子系统的交集，在实际应用过程中，可能不存在全局稳定解，即交集为空集的情况。

3 偏好集结型稳定解

如前文所述，由于全局稳定达到条件为苛刻，在实际应用过程中可能出现全局稳定为空集的情况。本部分从将不同情景下偏好进行集成为综合偏好的视角定义偏好情景应变式冲突系统G的另一种稳定解，即偏好集结型稳定解。

3.1 基于策略偏好序的偏好集结模型

推导决策者偏好是冲突分析的一项重要工作，Fang等学者[31]提出了策略权重排序法、策略优先权排序、直接排序等三种方法，其中策略优先权排序法不仅可以处理多状态复杂冲突系统的偏好排序问题，而且接近决策者判断冲突状态偏好的思考过程，被大量研究所采用[32]。因此本部分基于策略偏好序，提出一种多情景下不同偏好的集结模型，其基本思路是依据决策者对各潜在情景下冲突子系统的不同重视程度，将各潜在情景的偏好信息进行集结，以形成综合偏好信息集。

策略偏好序方法首先需要提供决策者的策略偏好描述Ω，其中越重要的策略描述排在越前方。一般策略偏好描述有三种类型：非条件型、条件型、双条件型。举例来说，假设某冲突系统有四种策略o1,o2,o3,o4。对于某决策者，其非条件型偏好描述为o2，表示决策者偏爱策略o2。某个状态中包含o2则该偏好描述为真。条件型描述为o1ifo3，表示决策者在选择策略o3的前提下，倾向选择o1策略，其中所有同时选择或不选择策略o1,o3的状态在该描述下都取真值(True)。双条件型描述类似为o3iffo4，表示决策者当且仅当先选择策略o4后才倾向选择策略o3。只有同时包含策略o3,o4的状态在该描述下取真值。

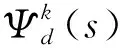
3.2 偏好集结型稳定求解步骤

在集结决策者不同潜在情景下冲突子系统的偏好信息后，可以根据经典冲突分析中有关Nash稳定，一般超理性稳定、对称超理性稳定和序列稳定的定义计算偏好情景应变式冲突系统的偏好集结型稳定解。需要指出的是，本文定义的偏好集结型稳定解假设冲突系统决策者对于各方的偏好信息以及潜在情景的重视程度等信息完全清楚，即这些信息是冲突系统的公共知识。下面给出偏好集结型稳定求解的主要步骤。

Step1集结偏好。依据定义9和定义10，将各潜在情景下冲突子系统的偏好集结成统一偏好。

Step2分析冲突系统的偏好集结型稳定。利用集结的偏好信息，按照经典冲突分析基本稳定的定义，即可推导偏好集结型稳定。偏好集结型稳定Nash稳定，一般超理性稳定、对称超理性稳定和序列稳定分别记为A-Nash，A-GMR，A-SMR，A-SEQ。

4 案例分析

本部分以某大型客机立项论证阶段的研制周期决策为例阐述本文方法。大型客机研制技术难度大，研制时间长，其研制周期需要考虑政策、竞争对手策略、客户需求偏好、国家工业基础和技术水平等众多因素。某大型客机研制周期决策过程涉及政府主管部门、客户、竞争者、主制造商等多方主体，且这些主体间利益诉求不同，形成了复杂的冲突关系。此外，由于航空产业受经济形势、国际关系等不稳定形势影响大，因此研制周期决策需要考虑未来不同的发展情景，需要利用本文提出的偏好情景应变式冲突分析模型进行分析。下面将详细阐述本文所提方法的步骤与均衡结果。

4.1 冲突建模与可行状态

某大型客机研制周期计划冲突系统包含四个决策者：政府主管部门(DM1)、主制造商(DM2)、客户(DM3)、竞争者(DM4)。这里考虑的政府主管部门的策略有：O1增加对主制造商的投资和O2 补贴客户，支持其增购大型客机；主制造商的策略为O3以较快进度完成大型客机研制工作；客户策略是O4增购大型客机；竞争者的策略为O5进行游说活动推销自己生产的大型客机。由于冲突系统共有5个策略，因此按照逻辑组合共有25=32种状态。这里需要剔除一些不可行状态，最后形成的可行状态集合如表2所示，其中Y和N分别代表选择或不选择某一项策略。

表2 可行状态集

4.2 情景生成与偏好分析

大型客机研制周期决策受到未来经济发展形势、产业政策等多方面影响。例如在预期经济形势乐观的情形下，大型飞机主制造商可能得到较好的经济与政策支持，因此主制造商偏向以最小周期向客户提供产品。客户在经济形势不乐观的情形下，可能趋向于不增购客机。因此，决策者的偏好是不确定的，是随着情景不断变化的(偏好情景应变)。本文选择经济走势、国际局势作为影响冲突系统偏好信息的主要情景要素，生成悲观情景、期望情景、乐观情景三个典型情景，如表3所示。

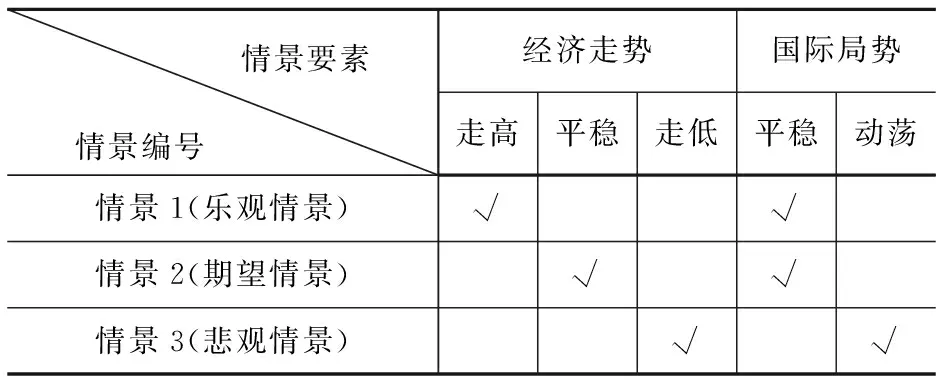
表3 典型情景表

前期实地调研了中国商飞上海飞机设计研究院、上海飞机客服中心等单位，根据调研结果具体整理分析三种典型情景下的决策者偏好信息情况。总体来说，在乐观情景下，经济形势走高，国际形势平稳，政府主管部门有能力投入资金，出台补贴政策，支持大型客机研制；而主制造商、客户和竞争者都对航空产业发展持积极态度。相反地，在悲观情景下，各决策者普遍不看好产业发展，其决策行为相对消极。在期望情景下，各情景要素处于正常水平，决策者根据常规情形进行偏好判断。具体形成的偏好如表4所示。下面介绍表4的含义，以情景1为例，政府主管部门偏爱客户增加订单，因此第一个偏好是4(4指表2中的第4个策略O4)；在政府主管部门增加投资的情形下，他希望主制造商选择压缩工期，即(3 IF 1)；此外，政府主管部门不希望竞争者的游说活动(O5)，即(-5),其中-代表厌恶此策略。其他含义类似，这里就不再赘述。

表4 决策者不同情景下策略偏好描述表

以表4所描述的情景3下策略偏好为例，将其输入到GMCR II软件中，可获得如下相对偏好关系：

DM1：s1≻s10≻s7≻s16≻s3≻s12≻s5≻s14≻s2≻s11≻s9≻s18≻s8≻s17≻s6≻s15≻s4≻s13

DM2：s9≻s18≻s8≻s17≻s6≻s5≻s15≻s14≻s4≻s2≻s13≻s11≻s7≻s16≻s3≻s1≻s12≻s10

DM3：s13～s12～s15≻s3～s4～s6≻s10～s11～s14≻s1≻s2～s5≻s16～s17～s18≻s7～s8≻s9

DM4：s1≻s2～s5≻s3≻s4～s6≻s7≻s8～s9≻s10≻s11～s14≻s12≻s13～s15≻s16≻s17≻s18

4.3 全局稳定分析

本部分分析某大型客机立项论证阶段研制周期决策冲突分析的全局稳定解。根据4.2小节给出的偏好描述，这里可以直接利用GMCR II软件进行分析，分析结果如表5所示。

表5 偏好情景应变式冲突分析模型稳定解

在乐观和期望情景下，状态10、14、16、18都是Nash均衡稳定。在这两种情形下，竞争者倾向于选择游说活动。而在政府主管部门增加投资或补贴的情况下，主制造商和客户需要分别压缩工期或增加投资。在悲观情况下，由于对未来发展看法悲观，各方均不采取行动(状态1)以及政府部门为保持未来竞争力增加投资而主制造商相应压缩工期(状态5)成为Nash均衡解，这基本符合实际情况。综合来看，该冲突系统只存在两种全局均衡，状态1和5是全局一般超理性稳定、全局对称超理性稳定。全局一般超理性稳定是指决策者的行动会受到其他决策者的反击而达到的均衡。全局对称超理性稳定是决策者在受到对手反击后自己仍然可以继续采取策略，但是行动后结局劣于初始情况而达到的稳定。综合考虑三种情景，冲突各方倾向于选择全不行动，或者仅仅由政府主管部门选择增加投资以使得制造商压缩工期。这种全局稳定相对来说十分严格，要求在各种情景下都达到稳定。

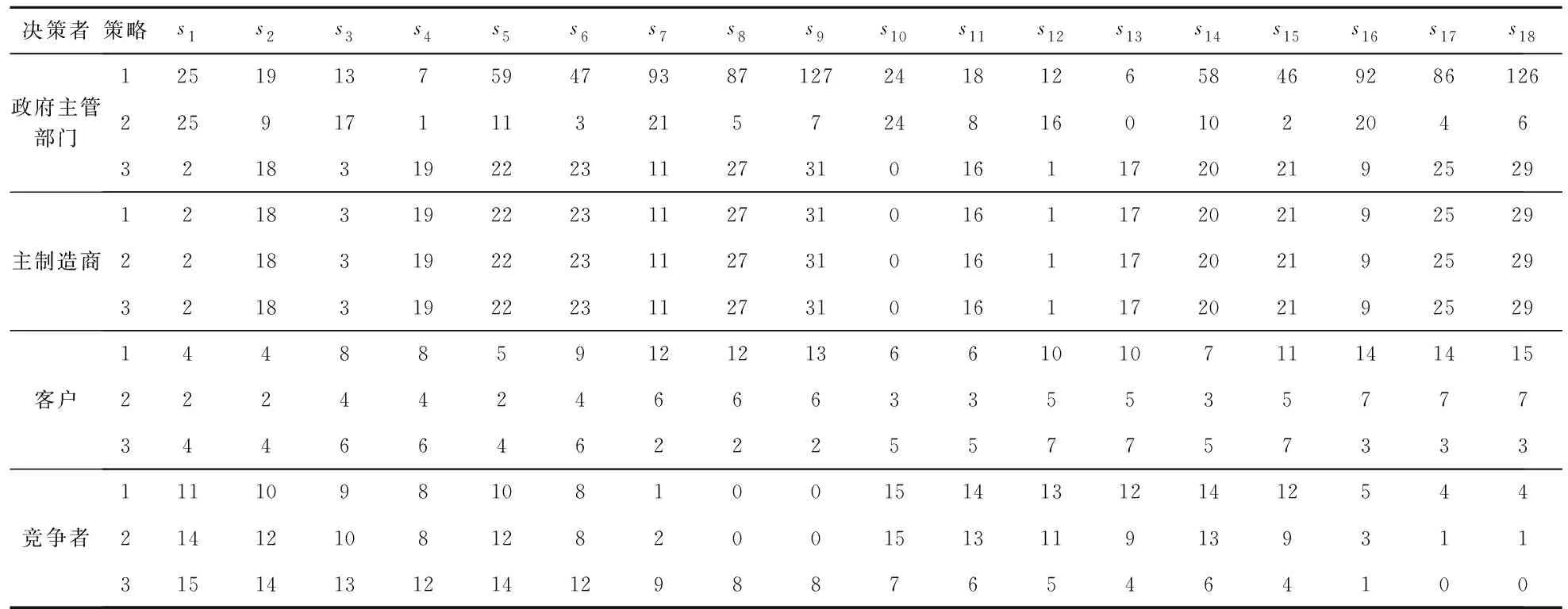
表6 各状态的偏好得分

4.4 偏好集结型稳定解分析

事实上，在实践中决策者由于自身判断对不同潜在情景的重视程度不同，可以利用偏好集结的思想先将各情景偏好集结成统一偏好，再利用本文定义的偏好集结型稳定分析冲突系统。首先根据定义9计算各状态的偏好得分，具体结果如表6所示。

4.5 两种稳定的对比分析

表5完整地展示了各潜在情景下冲突子系统稳定情况、全局稳定情况以及偏好集结型稳定情况，通过对比分析此表，我们总结了如下几条发现：(1)偏好型稳定包含全局稳定。表5中状态1和5是G-GMR和G-SMR，同时也是偏好集结型稳定。(2)全局稳定达到条件苛刻，偏好集结型稳定相对宽松。表5中全局稳定只有两个状态，而偏好集结型稳定有9种。(3)全局稳定只能在各潜在情景的稳定解中取交集，而偏好集结型稳定可能出现在潜在情景下的非稳定解。例如表5中，状态8,9,15不是任何潜在情景下的稳定解，但是属于偏好集结型稳定，这主要是因为偏好集结后导致了新的稳定产生。

5 结束语

考虑到冲突分析系统的决策者在不同潜在情景下可能拥有不同偏好信息，本文构建了偏好情景应变式冲突分析模型。首先利用情景分析技术构建决策者需要考虑的未来潜在情景。各潜在情景下的冲突子系统共同组成了偏好情景应变式冲突分析系统。针对此系统的均衡分析，本文从全局稳定和集结偏好两个角度分别设计了两类冲突均衡——全局稳定和偏好集结型稳定。全局稳定定义为各种潜在情景冲突子系统均衡的交集。全局稳定达到条件十分严格，可能存在全局稳定不存在的情况，因此本文进一步定义了偏好集结型稳定。具体来说，决策者需要先提供策略的偏好描述，进而计算各状态在各情景下的偏好得分，并利用决策者对各情景的重视程度将各情景下的偏好得分集结成统一得分，最后根据各状态的集结得分大小推导出决策者的偏好信息。在此基础上，利用GMCR II软件推导偏好集结型稳定。最后以某大型客机立项论证阶段的研制周期决策冲突为例说明本文方法的使用步骤和使用效果。案例结果表明偏好型稳定包含全局稳定，全局稳定条件苛刻，稳定数目少。

本文假设冲突模型的各决策者均了解对方在各潜在情景下的偏好信息以及对各潜在情景的重视程度，但是实践中可能存在决策者对对手的偏好等信息不确定的情况，下一步的工作是研究这种信息不对称环境下的偏好情景应变式冲突分析模型。此外，本文考虑是简单偏好，将来可以考虑基于强度偏好[33]将本文模型推广到强度偏好情景应变式冲突模型。