具有学习和退化效应的单机干扰管理问题
2019-02-15刘春来王建军
刘春来, 王建军
(1.杭州电子科技大学 管理学院,浙江 杭州 310018; 2.大连理工大学 管理与经济学部,辽宁 大连 116023)
0 引言
大量排序问题的研究中都假定工件的加工时间是一个常数,加工机器在整个加工过程中总是高效运行的;但在现实的环境中,工件的加工时间可能由于工人学习、退化等因素发生改变,机器的效率可能由于机器使用时间的过长而降低或出现故障。Browne和Yechiali[1]提出了具有退化工件的排序问题,也称为与开工时间有关的排序问题,这一模型已在钢铁工业、塑料工业、医疗行业及森林灭火等方面有许多应用[2~4],受到了越来越多的实践者和学者关注。Gawiejnowicz[5]在其《Time-dependent Scheduling》一书中对这一领域的相关术语和研究做了详细地介绍和探讨。Cheng[6]等人对加工时间与开工时间相关的排序问题的相关研究成果进行了总结,同时也进一步提出了一些具有挑战性的且尚未解决的难题。Biskup[7]首先将学习效应这一概念应用于排序问题中,证明了具有学习效应的单机极小化最大完工时间和总完工时间问题是多项式可解的,并且在文献[8]中总结了当前有关表示学习效应的不同函数类型,同时指出了未来研究发展的方向。
近年来,针对实际生产过程中面临的管理问题,同时考虑具有退化工件和学习效应的排序模型引发了工业界和学术界的广泛关注。Lee[9]对同时具有退化工件和学习效应的单机排序问题研究了两种加工时间的模型,并且在多项式时间内得到了问题的最优解。Wang和Guo[10]讨论了同时具有退化工件和学习效应的单机工期安排问题,构造了一个多项式时间算法解决所研究的问题。对于这方面的研究大多限定在单机问题上,更多有关退化和学习的模型可参考文献[11,12]。
在客观现实世界中,不确定性事件的发生是不可避免的,这就会对事先制定好的计划造成干扰。机器出现故障(维修)导致一段时间不可用就是其中的一类问题。在经典排序模型下,机器一段时间不可用问题得到了广泛地研究,具体读者可参见文献[13~15]。Ji[16]等考虑了一个具有简单线性退化工件的单机排序问题,首次将工件加工时间退化现象引入到机器可用性约束问题中。马英[17]等研究了机器带有一个不可用区间限制和工件加工时间退化的单机最大完工时间问题,提出了一种动态规划算法以得到最优解。Zhang和Luo[18]研究了具有退化工件且机器可用性限制下的平行机排序问题,提出了解决问题的一个近似多项式时间算法。
然而,大多数的重排序问题都集中于在新的环境下仍然考虑原目标如何最优,而本文的干扰排序模型既考虑了原目标又衡量了干扰事件造成的扰动。Qi[19]首先提出了干扰环境下机器排序干扰管理这一概念,并且研究了机器排序中常出现的几种干扰基本类型。刘锋[20,21]等人对单机干扰管理的几个模型进行了深入研究,Lee[22],Tang[23]对平行机干扰管理做了许多有意义的工作。胡祥培[24]等人对干扰管理的模型及其算法研究等做了分析综述。对于更详细的内容可参考文献[25,26]。Zhao和Tang[27]第一次尝试把干扰管理问题引入工件加工时间可变的新型排序模型中,对于具有简单线性退化的问题作了分析和探讨,但对于更复杂的或者更具有现实意义的新模型还没有涉及。除了文献[27]其它有关干扰管理的文献都是考虑加工时间为常数的情况,本文探讨在可预见性机器扰动环境下,工件加工时间既与开工时间有关又与其所在排序中的位置相关的单机排序问题。可预见性扰动是指当加工原始制定好的工件排序时获得干扰因素将会在未来某个时刻发生这一信息,得知干扰将会发生这一信息后,管理者会及时对原始排序进行调整。根据干扰度量函数的不同研究了两个问题,第一个问题的目标函数是总完工时间与总误工时间的加权和;第二个问题的目标函数是总完工时间与总提前时间的加权和。对于所研究的问题,首先证明了最优排序具有的性质,然后建立了相应的动态规划算法,并分析了算法的计算复杂度。
1 问题描述
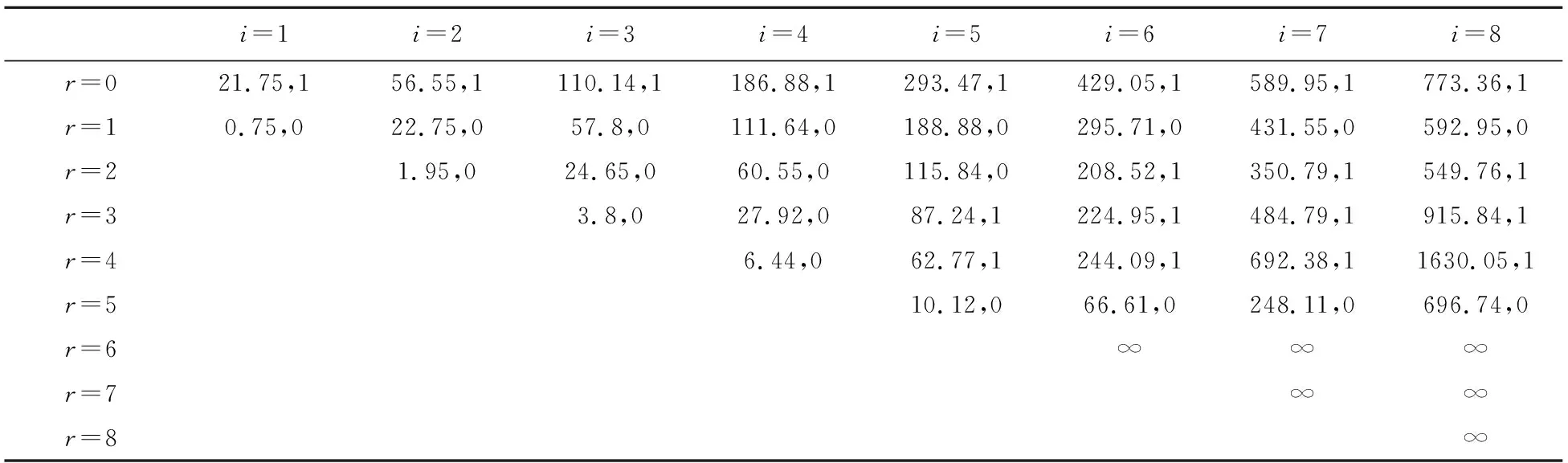
假设N={J1,J2,…,Jm}表示需要排序加工的工件集,所有工件在加工过程中都是不可中断的且在时刻t0>0都已到达,工件的实际加工时间是既与其开始加工时间又与其所在加工位置有关的函数。在本文中,定义αj表示工件Jj的恶化率且αj>0,sj表示工件Jj在机器上的开始加工时间,a表示工件的学习率且0 在工件的加工过程中,由于干扰事件的发生,导致原排序可能不再是最优排序,需要快速调整加工方案以便在兼顾原最优目标情况下降低干扰事件造成的影响。在可预见性扰动模型下,管理者一旦得知相关的扰动信息,则立即将未加工的工件(假设个数为n,n≤m)从1到n重新标号并且重置此时刻为0,本文后面涉及的工件序号都是对未加工工件而言的。令ΔM表示机器发生中断干扰,即当干扰发生时机器会有一段时间不可用,机器这段不可用时间记为[ta,tb](ta≥min{αjt0},1≤j≤n),当机器中断结束后,学习效应将重新开始。 本文考虑两个涉及机器干扰的单机排序问题,第一个问题的目标函数是极小化总完工时间与总延误时间的加权和,第二个问题的目标函数是极小化总完工时间与总提前时间的加权和。沿用文献Qi[19]中的目标函数,使用三参数表示法问题可记为: 1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣTj (1) 1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣEj (2) 其中α,β≥0。 考虑到极小化总完工时间的单机排序问题1|Δm,αjsj,pred-mgt|ΣCj是NP-困难的(文献[16]),而这一问题又是本文所研究问题的特殊情形(a=1,α=1,β=0)。因此,本文所研究的问题(1)和(2)都是NP-困难的。 引理1对问题1|pjr=αjsjar-1|Cmax,给定排序π=[J[1],…,J[n]],工件J[1]的开工时间为t≥t0,那么。 (3) 证明对于任意给定的一个排序π,安排在第一个位置上加工的工件的实际加工时间为p[1]=α[1]t,完工时间为C[1]=t+p[1]=t(1+α[1]);相似地,可得 引理2[12]对于问题1|pjr=αjsjar-1|ΣCj,按照工件恶化率αj的非减序排列可得问题的最优排序(SDR规则)。 定理1对于问题1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣTj,存在一个最优解决方案使得排在ta时刻前的工件按SDR规则排列,排在tb时刻后的工件按SDR规则排列。 证明考虑一个最优排序σ,在此最优排序中两个相邻工件Jk和Jj,Jk在Jj前一个位置加工且αk≥αj,假设Jk的开始加工时间为t1,处在最优排序的第k个位置,那么有 Ck=t1+αkt1ak-1 Cj=Ck+αjCkak=t1+(αk+αja+αkαjak)t1ak-1 交换工件Jk和Jj的位置得到一个新的排序σ′,在新排序中σ′,有 由此可得 (4) =(αj+αka-αk+αkαjak)t1ak-1 由此可得 (5) (6) (7) 基于定理1的结论,下面给出求解问题(1)的一个动态规划算法: 将n个工件按SDR规则重新排序,即α1≤α2≤…≤αn,由定理1可知,工件J1一定是排在ta时刻前的第一个工件,或tb时刻后的第一个工件。如果工件J1是排在ta时刻前的第一个工件,那么工件J2一定是排在ta时刻前的第二个工件或者tb时刻后的第一个工件;如果工件J1是排在tb时刻后的第一个工件,那么工件J2一定是排在ta时刻前的第一个工件或者tb时刻后的第二个工件。由此,对一个给定的工件集σi=[J1,J2,…,Ji],(i=1,2,…,n),工件Ji一定是排在ta时刻前的最后一个工件或者tb时刻后的最后一个工件。 假设x表示排在ta时刻前的工件的加工时间表长,y表示排在tb时刻后的工件的加工时间和,r表示排在ta时刻前工件的个数(排在tb时刻后的工件个数为i-r且tb时刻后工件的学习效应重新开始),(i,x,y,r)表示工件集σi所对应的状态,f(i,x,y,r)表示在状态(i,x,y,r)下对应的目标函数值。 动态规划算法如下: (3)最优值为min{f(n,x,y,r)} 在目标函数中存在真实提前时间这一问题下,需要对α≥β和α<β两种情况分别进行考虑。 引理3对于问题1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣEj,当α≥β时,存在最优排序满足相邻工件间没有空闲时间。 证明考虑最优排序σ=[J[1],…,J[n]],如果工件J[i]前存在空闲时间,那么向前移动工件J[i]直到工件J[i-1]和工件J[i]之间没有空闲,假设工件J[i]向前移动了Δt个时间单位,那么完工时间减少α[j]Δtai-1了,提前的时间量最多增加α[j]Δtai-1,由于α≥β,所以向前移动工件消除相邻工件间的空闲时间,总目标函数值不会增加。 定理2对于问题1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣEj,当α≥β时,存在一个最优方案使得排在ta时刻前的工件按SDR规则排列,排在tb时刻后的工件按SDR规则排列。 证明考虑一个最优排序σ,在此最优排序中两个相邻工件Jk和Jj,Jk在Jj前一个位置加工且αk≥αj,假设Jk的开始加工时间为t1,处在最优排序的第k个位置,那么有 Ck=t1+αkt1ak-1 Cj=Ck+αjCkak=t1+(αk+αja+αkαjak)t1ak-1 交换工件Jk和Jj的位置得到一个新的排序σ′,在新排序σ′中,有 由(4)式可得 (8) 由此可得 (9) ≤(αk-αJ)t1ak-1 (10) 基于以上两种情况可得 (11) 基于定理2的结论,建立解决问题1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣEj的一个动态规划算法: 动态规划算法如下: (3)最后,min{g(n,x,y,r)}就是所求的最优值。 当α<β时,在最优排序中相邻工件间可能出现空闲时间,所以引理3和定理2中的最优性条件不再成立,本文不做探讨,后续对其进行研究。 针对本文所构建的动态规划算法,使用MATLAB开发语言,在MATLAB R2012b 8.0.0.783版本环境下实现。 假定有8个未加工的工件,对应的恶化率和初始最优排序时工件的实际加工时间见表1,重置的开始加工时间t1=1,学习率a=0.6,中断的起始时刻ta=9,结束时刻tb=15,加权因子分别为α=0.5,β=0.5。表2和表3中的二维向量(f,ξ),其中f表示当前状态下对应的目标函数值,ξ={0,1}分别表示当前状态下工件Jj排在中断前或中断后的最后位置,表中涉及的数据均保留两位小数。 经过运算得到问题一的最优目标函数值fmin=549.76,根据递归过程计算出的数值通过逆向追踪法得出工件的加工顺序为[4,5,1,2,3,6,7,8],其中工件J4,J5排在中断前加工,J1,J2,J3,J6,J7,J8排在中断后加工(见表2)。 经过运算得到问题二的最优目标函数值fmin=288.52,根据递归过程计算出的数值通过逆向追踪法得出工件的加工顺序为[4,5,1,2,3,6,7,8],其中工件J4,J5排在中断前加工,J1,J2,J3,J6,J7,J8排在中断后加工(见表3)。 表1 工件相关参数 表2 动态规划迭代结果(问题一) 表3 动态规划迭代结果(问题二) 在客观现实世界中,不确定性事件的发生总是不可避免的。面对干扰事件引发的影响,如何使系统尽快恢复使干扰产生的扰动尽量减少是决策者需要考虑的重要问题。本文考虑了在可预见性机器扰动环境下,工件实际加工时间既与开工时间有关又与其所在排序中的位置相关的单机排序问题,可预见性扰动是指当加工原始制定好的工件排序时获得干扰因素将会在未来某个时刻发生这一信息,同时在得知干扰将会发生这一信息后,会及时对原始排序进行调整。考虑两种不同的测量扰动大小的优化问题,第一个问题的目标函数是极小化总完工时间和总误工时间的加权和;第二个问题的目标函数是极小化总完工时间和总提前时间的加权和。最后,分别得到了解决问题的动态规划算法。对本文没做探讨的情况α<β可进一步的研究,且可考虑在干扰环境下的平行机或流水车间作业问题。
2 问题1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣTj



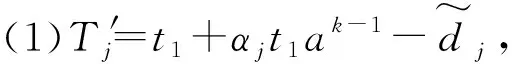











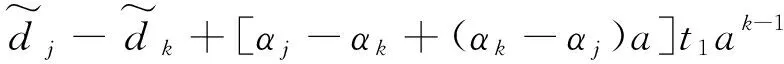
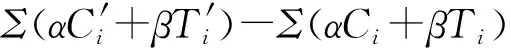


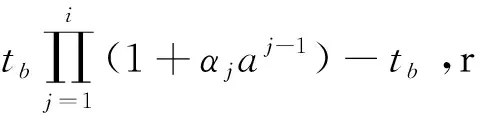

3 问题 1|Δm,αjsjar-1,pred-mgt|αΣCj+βΣEj

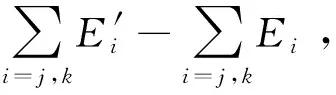









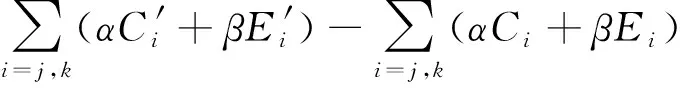




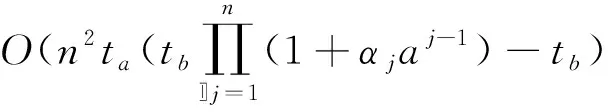
4 数值算例


5 结论
