考虑码头内外堆场竞争的集装箱堆存定价模型

孙赫迎， 曾庆成

(大连海事大学 航运经济与管理学院, 辽宁 大连 116026)

0 引言

集装箱码头作业包括装卸船作业、堆场作业、集疏运作业。其中堆场最初用于临时堆存货物，以保证多种运输方式之间的流畅衔接，后来逐渐被货主和物流服务供应商视为低廉的货物堆存仓库。随着码头堆场需要堆放的集装箱数量不断增加，堆放层数越来越多，导致码头翻箱成本增加、外集卡等待时间增长、堆场拥堵等问题，从而降低了码头作业效率，并影响集装箱供应链的整体效率。

为了缓解码头堆场堆存压力，专门用于堆存集装箱的堆场应运而生，即集装箱场外堆场。将码头堆场堆存的部分集装箱转移至场外堆场，有助于缓解码头堆场拥堵，减少翻箱次数，提高码头堆场作业效率，从而提高集装箱供应链的整体效率。然而，如何处理码头内外部堆场之间的竞争与合作关系，通过合理堆存定价策略引导箱流，已成为需要决策的关键问题。

集装箱码头是港口供应链上重要的货物集散节点，而堆场是集装箱码头作业系统的关键环节之一。其作业效率直接影响码头整体水平。国内外学者针对堆场管理开展了大量研究，研究主要分为堆存计划、机械调度与翻箱优化等。码头堆场最初用于货物的临时堆存，后来逐渐被货主和物流服务供应商视为低廉的货物堆存仓库。货物堆存时间和堆存数量增加制约了堆场的工作效率和设备利用率。(Steenken等[1]；Rodrigue和Notteboom[2]；Fransoo和Lee[3])。因此，如何通过堆存定价减少码头堆场拥堵，提升效率受到越来越多的关注。如，Meersman等[4]基于边际成本理论研究港口的定价机制。Holguín-Veras和Jara-Díaz[5]拓展了传统的差别定价理论，研究港口的空间分配和多等级集装箱的堆存定价问题。Holguin-Veras和Jara-Díaz[6]研究到港集装箱数量与堆存价格相关时的堆存定价问题。Qiu等[7]研究在物流中心堆存的动态定价问题。随着码头堆场有限的土地资源不断制约港口的发展，Castilho和Daganzo[8]首先提出了场外堆场的概念，基于两种定价策略研究存在和不存在场外堆场时的定价方案。Kim和Kim[9]研究只存在一家外堆场的进口箱的最优堆存定价问题。Fransoo和Lee[10]指出在码头堆场和场外堆场竞争条件下，如果进口箱堆存价格太低，码头堆场就会成为客户的远程仓库。Chung-Yee Lee和Mingzhu Yu[11]在只存在一家场外堆场的理想条件下，构建非合作博弈模型，分析码头堆场和外堆场的定价决策。E. Martín和J. Salvador 和 S. Saurí[12]研究进出口箱量是随机变量的码头堆场最优堆存定价策略，考虑堆场空间利用率构建进口箱最优堆存定价策略模型。

现有文献虽然从堆存定价方面开展研究，但考虑码头堆场和多家场外堆场之间竞争的堆存定价问题尚未解决。为此，本文构建两阶段内外堆场定价模型，研究基于货主选择行为的堆场定价决策问题，分析堆场定价对货主堆存决策的影响，揭示码头堆场定价与码头堆场操作成本、场外堆场运输成本、货主需求影响参数之间的内在关系，为码头如何通过堆存定价，提高作业效率提供依据。

1 模型构建

1.1 问题描述

针对由一个码头堆场和两个场外堆场所构成的内外堆场堆存系统，构建集装箱码头堆存定价模型，探究码头堆场收益的影响因素。假设货主和堆场都为风险中性和完全理性，即两者将根据收益最大化的原则来进行决策。

为了反映货主堆存决策和堆场定价决策过程，构建基于斯坦伯格(Stackelberg Game)理论的两阶段内外堆场定价模型，其中，堆场是博弈的领导者，货主是博弈的追随者。第一阶段构建堆场定价模型，码头堆场和两家场外堆场考虑货主选择行为，进行堆存定价的决策；第二阶段构建货主堆存决策模型，货主考虑堆场定价行为，决定集装箱转移时刻。

假定货主进口箱量为Q，集装箱卸船后全部在码头堆场进行堆存。若堆存时间T在码头堆场的免费期F之内，货主免费堆存；一旦堆存时间超过免费期，货主需要向码头堆场支付额外的堆存费用p0。在码头堆场之外还有两家场外堆场，货主可以选择在免费期结束之后的某一时刻t0将在码头堆场堆存的部分集装箱q1，q2分别运至场外堆场1和2堆存，剩下的集装箱q0继续堆存在码头堆场。

1.2 堆场定价模型

构建两阶段内外堆场定价模型，第一阶段是堆场定价模型，分别得到码头堆场和场外堆场的最优均衡定价。第二阶段是在第一阶段模型的基础上设计货主堆存决策模型，得到货主的最优转移时刻。

参数设置：

第二阶段 货主成本模型

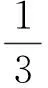
(1)

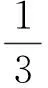
(2)

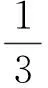
(3)

货主成本函数：

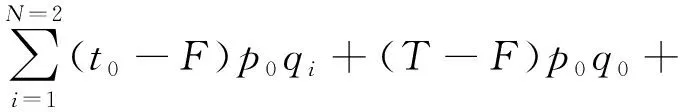
(4)

货主不移箱的成本函数:

C0=(T-F)Qp0

(5)

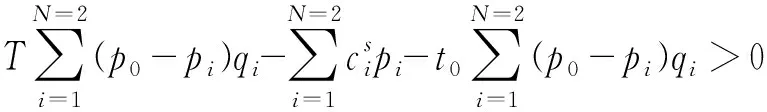
(6)

第一阶段 堆场定价模型：

第二阶段货主根据成本最小化的原则，做出货主最优移箱时刻的决策，然后基于最优移箱时刻构建堆场收益模型。

码头堆场的收益函数

π0=-cF2(q0+q1+q2)

+[p0(T-F)-c(T-F)2]×q0

(7)

其中，q0是转移时刻t0后货主选择继续堆存在码头堆场的集装箱数量；q1是货主转移至场外堆场1的集装箱数量；q2是货主转移至场外堆场2的集装箱数量。Lee和Yu[11]提到港口堆场大小有限，单位集装箱操作成本是集装箱堆存时间的二次函数。

定理2码头堆场的收益函数π0是关于堆存价格p0的凹函数，最优定价为

证明码头堆场的收益函数π0对堆存价格p0的一阶导数和二阶导数

一阶导数为：

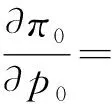
码头堆场收益函数关于堆存价格的二阶导数为负值，令∂π0/∂p0=0，即可求出码头堆场的最优定价，实现码头堆场收益最大化。

(8)

场外堆场i的收益函数

πi=(T-t0)(pi-ci)qi

(9)

定理3场外堆场i的收益函数是关于堆存价格pi的凹函数，最优定价为

证明场外堆场i的收益函数πi关于堆存价格pi的一阶导数和二阶导数

场外堆场1的收益函数π1是关于单箱堆存价格p1的凹函数，令∂π1/∂p1=0可求出p1。同理得到p2的表达式。

(10)

(11)

联立式(8)、(11)、(12)，可得最优定价：

(12)

(13)

(14)

引理4(1)码头堆场的最优堆存箱量、最优堆存定价和利润分别关于两家场外堆场运输成本的单调递增函数。

(2)场外堆场1的最优堆存箱量、最优定价和利润分别关于场外堆场1运输成本的单调递减函数。场外堆场2的最优堆存箱量、最优堆存定价和利润分别关于场外堆场1运输成本的单调递增函数。场外堆场2运输成本的情况类似。

(3) 码头堆场的最优堆存箱量是关于码头堆场操作成本的单调增函数。码头堆场的最优堆存定价和利润是关于码头堆场操作成本的单调递减函数。

(4)场外堆场i的最优堆存箱量、最优堆存定价和利润是关于码头堆场操作成本的单调增函数。

引理5(1)码头堆场的最优堆存箱量是关于堆场定价对货主需求影响系数b的单调递减函数。两家场外堆场最优堆存箱量是关于b的单调递增函数。随着b的增加，当c2>c1时，堆场1的堆存箱量相比于堆场2变化的更敏感。

(2)码头堆场的最优堆存定价是关于堆场定价对货主需求影响系数b的单调递减函数。两家场外堆场的最优堆存定价是关于b的单调递减函数。随着b的增加，当c2>c1时，场外堆场1的堆存定价相比场外堆场2变化的更敏感。

(3)码头堆场和场外堆场的收益函数是关于堆场定价对货主需求影响系数b的单调递减函数。

2 算例分析

2.1 运输成本对堆场的影响

2.2 码头堆场操作成本c对堆场的影响

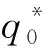
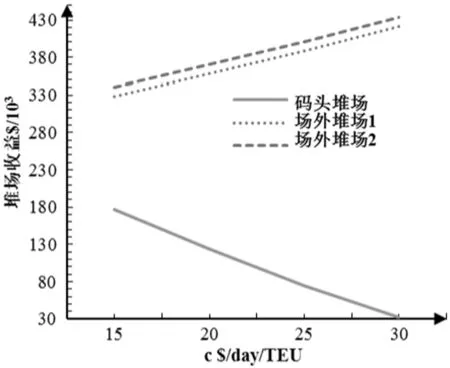
图6 码头堆场操作成本c对堆场定价π*的影响 图7 b对堆场收益π*的影响

2.3 货主需求参数对堆场的影响

堆存定价对货主需求的影响系数b对堆场收益的影响如图7所示，根据引理5可知，堆场收益函数是关于堆场定价对货主需求影响系数b的单调递减函数。当其他堆场定价对货主需求的影响程度逐渐增加，即竞争越来越激烈，堆场收益均下降。

运输成本对货主需求的影响系数d对堆场收益的影响如图8所示，根据引理5可知，码头堆场收益函数是关于运输成本对货主需求影响系数d的单调递增函数。场外堆场收益函数是关于运输成本对货主需求影响系数d的单调递减函数。当运输成本对货主需求的影响程度越来越强，对码头堆场更有利。

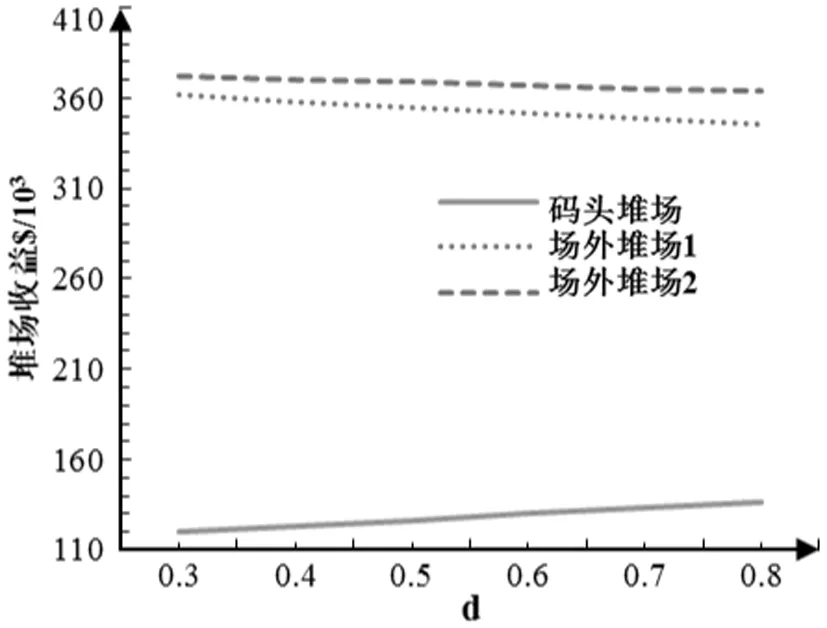
图8 d对堆场收益π*的影响

3 结论

本文分析了码头堆场和两家场外堆场之间的堆存价格竞争，这种竞争关系在实践中存在，场外堆场的存在不仅可以缓解港口堆场拥堵，而且有助于减少客户的堆存成本。构建两阶段博弈模型，研究堆场定价决策、货主堆存决策行为。结果表明，一旦过了免费期立刻移箱到场外堆场，货主成本最小。同时，对于码头堆场来说，当两个场外堆场的运输成本增加时，货主选择堆存在码头堆场的箱量增加，码头堆存定价增加，提高码头堆场收益。当码头堆场操作成本降低，码头堆场堆存价格随之下降，货主在码头堆存箱数量增加，码头堆场收益增加。

本文为码头内外堆场的堆存定价决策提供理论基础，为提高集装箱供应链的整体效率提供思路。本文仅考虑一个货主、一个码头堆场与两家场外堆场的决策行为，且假设货主的集装箱数量不变。由于货主堆存的集装箱数量随堆存价格上下波动。因此，在实际中，还可以对堆存定价的多主体决策行为与货主堆存数量的不确定性等问题进行深入研究。本文码头堆场和两家场外堆场之间是竞争关系，因此也可以深入探讨码头堆场和多家场外堆场是合作关系下的定价决策问题。